Геометрические задачи с элементами алгебры и наоборот

На этой странице вы узнаете

• Что появилось первее: алгебра или геометрия?
• Что такое пифагоровы тройки и как их использовать?
• Как разрезать торт на 8 кусков за три движения?

В этой статье мы с вами узнаем парочку лайфхаков, которые помогут решать геометрические задачи с помощью алгебры, а алгебраические — с помощью геометрии. Приступим!

Геометрические задачи с элементами алгебры

Начнем с геометрических задач. Иногда они кажутся сложнее, нежели алгебраические, поэтому сейчас мы посмотрим, как их можно решить с помощью алгебры. 

Что появилось первее: алгебра или геометрия? Геометрия появилась раньше, чем алгебра. Геометрия занималась изучением форм и пространства еще в древних цивилизациях, таких как Египет и Вавилон. Алгебра возникла позже, в 3 веке до н.э., когда Диофант из Александрии написал первый трактат по алгебре.

Начнем сразу с примера такой задачи из ЕГЭ.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №1. 

Задание. Диагонали ромба относятся как 3:4. Периметр ромба равен 400. Найдите высоту ромба. 

Решение. Пусть диагонали ромба равны \(6х\) и \(8х\), так как можно составить пропорцию \(6x:8x=3:4\). Рассмотрим прямоугольный треугольник ABO. В нем по теореме Пифагора найдем гипотенузу AB.

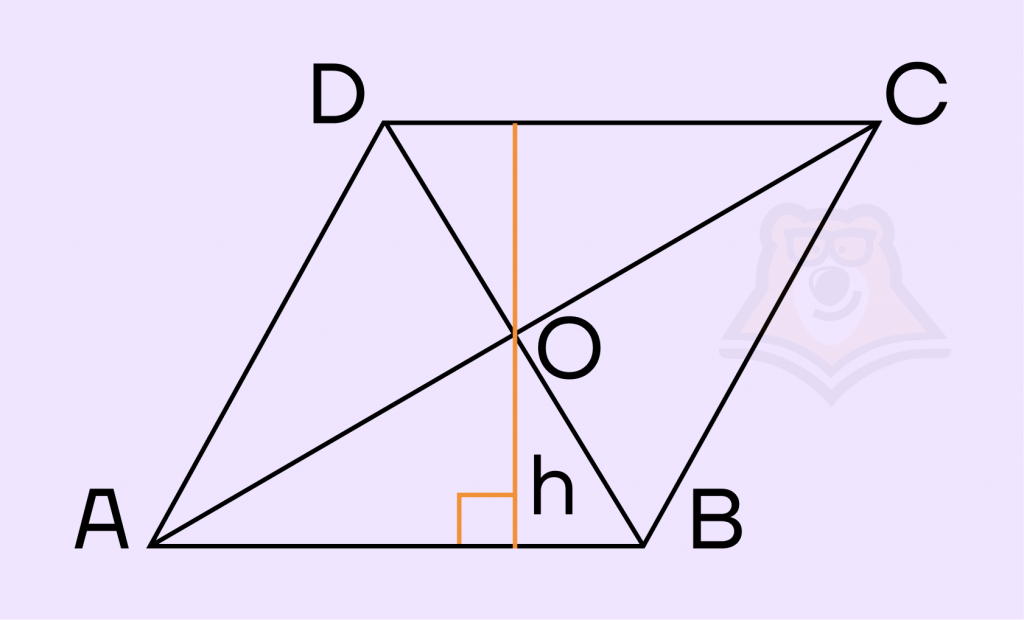
\(AB^2=AO^2+OB^2\)
\(AB^2=9x^2+16x^2\)
\(AB^2=25x^2\)
\(AB = 5x\)

Так как \(P = 400\), то:

\(5x*4=400\)
\(x=20\)

Тогда AB:

\(AB=5*20=100\)

А диагонали равны:

\(6x=120\)
\(8x=160\)

Теперь, чтобы найти высоту, можем воспользоваться формулами площади ромба:

\(S=\frac{1}{2}*d_1*d_2\)
\(S=ah\)
\(\frac{1}{2}*d_1*d_2=ah\)
\(\frac{1}{2}*120*160=100*h\)
\(h=96\)

Ответ: \(96\)

Как вы можете заметить, мы использовали много формул, в особенности формулы площади. Решение геометрических задач с помощью формул площадей называется методом площадей. 

Метод площадей и метод объемов мы разбирали в другой нашей статье — «Периметр, площадь и объем». Эти методы помогают решить геометрические задачи с помощью алгебры.

Помимо этого, задачи с векторами тоже можно решать не только геометрически, но и алгебраически. 

Пример 1. Перпендикулярны ли векторы \(a=\{1, 5, -2\}, b=\{3, -1, 9\}\)?

Решение. Не будем строить эти векторы, а используем алгебру. Векторы перпендикулярны, если их скалярное произведение равно нулю. Формула скалярного произведения выглядит так:

\(\vec{a}*\vec{b}=x_1x_2+y_1y_2+z_1z_2\)

Посчитаем скалярное произведение для векторов a и b:

\(\vec{a}*\vec{b}=1*3+5*(-1)+(-2)*9=-20\neq 0\)

Раз скалярное произведение не равно 0, то векторы не перпендикулярны. 

Ответ: не перпендикулярны.

С примерами геометрических задач, которые можно решить с помощью алгебры, разобрались. Теперь можем переходить к задачам алгебры с использованием геометрии.

Задачи алгебры с использованием геометрии

Хоть алгебраические задания и легче, чем геометрические, их все равно нужно уметь решать разными способами, чтобы точно быть уверенным в правильном ответе. 

Перейдем к примеру, чтобы посмотреть, как можно решать алгебраические задачи с помощью геометрии.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №6. 

Задание. Решите уравнение \(\sqrt{64+x^2}=10\). В ответ запишите больший из корней.

Решение. Абстрагируемся от того, что это — алгебраическое уравнение. Давайте рассмотрим прямоугольный треугольник, у которого гипотенуза равна 10, один катет равен 8, а второй — х. Тогда получим обычную теорему Пифагора. Соответственно, подставляем числа в формулу теорему Пифагора:

\(10^2=8^2+x^2\)
\(100 = 64+x^2\)
\(x^2=36\)
\(x=\pm 6\)

Соответственно, корни равны \(x=\pm 6\). Так как в ответе нужно записать больший из корней, ответом будет \(6\).

Ответ: \(6\)

Получается, мы можем решить иррациональные уравнения с помощью теоремы Пифагора. 

Что такое пифагоровы тройки и как их использовать? Пифагоровы тройки — тройки натуральных чисел, которые удовлетворяют теореме Пифагора. Вот таблица, в которой показаны первые 7 пифагоровых троек: Пифагоровы тройки можно использовать на экзамене для быстрого подсчета, если вам попалась теорема Пифагора. Чаще всего используются первые 3 пифагоровы тройки.

Теперь давайте решим еще одно задание.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №10. 

Задание. Завод решил уменьшить выпуск продукции на 20%. На сколько процентов нужно увеличить выпуск продукции, чтобы достигнуть прежнего уровня? Ответ запишите без знака процента.

Решение. Рассмотрим чертеж:

Отрезок \(AB\) — первоначальный выпуск продукции, который мы разделили на 5 равных частей. После того, как сократили выпуск продукции на 20%, он стал равен отрезку \(AC\), то есть мы убрали часть \(CB\), которая и равна 20%. 

Теперь, чтобы вернуть первоначальный выпуск продукции, нужно найти, какую часть составляет CB от AC. Ответ виден из чертежа — \(\frac{1}{4}AC=CB\). Соответственно, имеем:

\(\frac{1}{4}*100\%=25\%\)

Получается, нужно увеличить на 25%. Ответ записываем без знака процента.

Ответ: 25

Почти все текстовые задачи можно решить с использованием геометрии. Решение текстовых задач мы разбирали в статье «Текстовые задачи».

Как разрезать торт на 8 кусков за три движения? Следите за движениями: Сначала разрезаем торт на две части. У нас получилось два больших куска. Теперь еще раз разрезаем торт, и у нас получается 4 части.  И последнее движение: мы разрезаем торт не по вертикали, а по горизонтали. И у нас получилось как раз 8 кусков.

В этой статье мы разобрали, как можно решать геометрические задачи с помощью алгебры и наоборот. В следующий раз мы узнаем, как решать задачи с параметрами.

Термины

Иррациональные уравнения — это уравнения, в которых неизвестное находится под знаком корня.

Фактчек

• От геометрических задач можно перейти к алгебраическим с помощью метода площадей и метода объемов.
• В задачах с векторами их необязательно строить — можно использовать алгебраические формулы, которые сильно ускоряют процесс решения.
• Для решения иррациональных уравнений можно использовать теорему Пифагора.
• И текстовые задачи из ЕГЭ по профильной математике можно тоже решать с помощью геометрии.

Проверь себя

Задание 1.
Диагонали ромба относятся как 3:4. Периметр ромба равен 100. Найдите высоту ромба.

1. \(24\)
2. \(96\)
3. \(48\)
4. \(192\) 

Задание 2.
Перпендикулярны ли векторы \(a=\{2, 10, -4\}, b=\{6, -2, 18\}\)?

1. Да.
2. Нет.

Задание 3.
Какая из этих троек не является пифагоровой? 

1. 3, 4, 5
2. 6, 8, 10
3. 8, 15, 17
4. 5, 11, 12

Задание 4.
Завод решил уменьшить выпуск продукции на 10%. На сколько нужно увеличить выпуск продукции, чтобы достигнуть прежнего уровня? Ответ запишите в виде обыкновенной дроби.

1. \(11.1\%\)
2. \(\frac{1}{10}\)
3. \(\frac{1}{9}\)
4. \(10\%\)

Ответы: 1. — 1; 2. — 2; 3. — 4; 4. — 3.