Финансовые задачи. Проценты.

На этой странице вы узнаете

• Как найти процент от пирога?
• Как смешать цвета и получить проценты?
• Как с помощью нескольких кусочков восстановить весь оставшийся пирог?

Мы всё любим выгоду. Скидки, акции, карта постоянного клиента — приятные плюшки в шопинге, не так ли? Мы экономим благодаря тому, что магазины снижают стоимость товара на определенное количество процентов. 

Но можно получать выгоду и от повышения процента. В каком случае? Если мы делаем вклады в банки. Любое повышение суммы вклада на процент означает, что мы стали чуть-чуть богаче.

Проценты

С процентами мы сталкиваемся почти ежедневно. Настало время разобраться, что это такое.

Процент — это одна сотая часть от чего-то. 

То есть мы делим какую-то величину на 100 равных частей и берем из них только одну. Проценты обозначаются знаком “%”

Как найти процент от пирога? Возьмем очень-очень большой пирог и разрежем его на 100 равных частей. Весь пирог будет равняться 100%. Каждый получившийся кусочек будет равен одному проценту от этого пирога.

Через процент мы можем найти, какую долю от целого составляет взятая часть. Это может быть половина, четверть или десятая, и любое из данных отношений можно записать через процент. То есть процент показывает, какое количество равных частей (из 100) мы берем от числа или величины. 

Рассмотрим число 100. Пусть это будет не просто абстрактное число, а 100 рублей. 

Один процент от 100 рублей будет по определению равен 100100=1 рубль. 

Как найти проценты

Чтобы найти какое-то определенное количество процентов от числа, нужно это количество умножить на 1% от числа. 

Например, 9% от 100 рублей будет \(9*\frac{100}{100}=9\) рублей. 
57% от 100 рублей будет \(57*\frac{100}{100}=57\) рублей. 

Этим способом можно найти любой процент от любого числа. Возьмем 5290 рублей и найдем от них 25%:
\(25 * \frac{5290}{100} = 25 * 52,9 = 1322,5\: рублей\). 

Алгоритм №1 для нахождения процента от числа 1 шаг. Разделить данное число на 100. Таким образом мы найдем 1% от числа. 2 шаг. Умножить получившееся значение на количество процентов, которое необходимо найти.

Пусть r — искомый процент от числа А, n — сам процент. Тогда справедлива формула: 

\(r = \frac{А}{100} * n\) 

Например, нужно найти 83% от числа 3216, тогда по формуле: 

\(r = \frac{3216}{100} * 83 = 32,16 * 83 = 2669,28\)

Чтобы найти процент от числа, можно также умножить это число на процент, деленный на 100. 

На самом деле, это будет та же формула, что мы вывели ранее, но с небольшими преобразованиями. 

Рассмотрим выведенную ранее формулу: 

\(\frac{A}{100} * n = \frac{A * n}{100} = \frac{n}{100} * A\).

Найдем 30% от 450: 
\(\frac{30}{100} * 450 = 0,3 * 450 = 135\).

Алгоритм №2 для нахождения процента от числа 1 шаг. Разделить количество процентов на 100. 2 шаг. Умножить получившееся значение на данное в условии число.

Пользоваться можно любым из этих алгоритмов. 

Иногда проценты могут представлять из себя простые дроби. 

• 50% — это ровно половина от числа, поэтому число можно сразу разделить на 2.
  50% от 20 будет \(\frac{20}{2} = 10\).

• 25% — это четверть от числа, поэтому число можно сразу разделить на 4. 
  25% от 400 будет \(\frac{400}{4} = 100\).

• 20% — это пятая часть от числа, поэтому число можно сразу делить на 5. 
  20% от 1000 будет \(\frac{1000}{5} = 200\).

• 10% — это десятая часть от числа, поэтому число можно сразу делить на 10. 
  10% от 350 будет \(\frac{350}{10} = 35\). 

Но если мы можем найти процент от числа, как найти число по его проценту? 

Как с помощью нескольких кусочков восстановить весь оставшийся пирог? Допустим, у нас есть 4 кусочка пирога, и мы знаем, что каждый кусочек – 1% от него. По этим кусочкам мы можем восстановить все остальные части и найти целый пирог. Достаточно найти или сделать еще 96 таких же кусочков, чтобы вместо 4% получить 100%, то есть целый пирог.

Если мы знаем, что несколько кусочков равны между собой и составляют определенный процент от пирога, допустим, 10%, нужно восстановить оставшиеся 90% из точно таких же кусочков. 

Алгоритм нахождения числа через процент 1 шаг. Выяснить, чему равен 1% от нужного числа; 2 шаг. Умножить полученное значение на 100.

Например, мы знаем, что 4500 — это 3% от какого-то числа. Действуя по этому алгоритму, решаем задачу: 

Если 4500 — это 3%, то 1% будет равен \(\frac{4500}{3} = 1500\).
Теперь умножаем полученное значение на 100: 1500 * 100 = 150000. 
Ответом будет число 150000. 

В более сложных задачах можно воспользоваться пропорцией. 

Пропорция — это равенство между двумя отношениями. 

Пропорцию можно представить в виде \(\frac{a}{b} = \frac{c}{d}\) или a : b = c : d, где a, d — крайние члены пропорции; b, c — средние члены пропорции. 

Они так называются не просто так: крайние члены стоят с краю, а средние между ними.

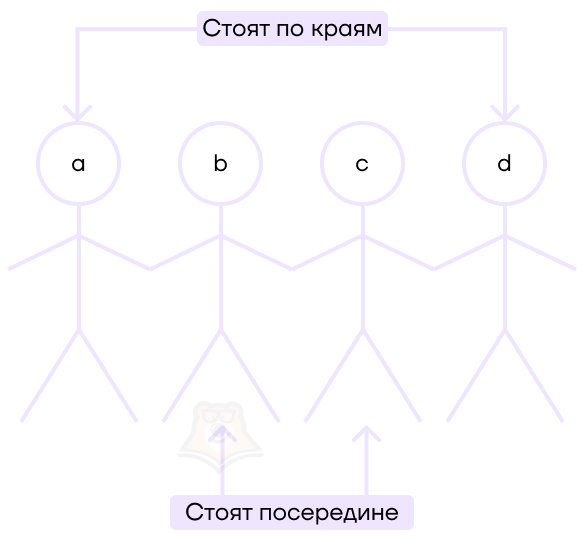
Например, можно составить пропорцию: \(\frac{8}{4} = \frac{25}{12,5}\), где 8 : 4 = 2   и 25 : 12,5 = 2, то есть равенство выполняется. 

Для пропорции будет справедливо уравнение a * d = b * c, то есть мы умножаем части дроби крест-накрест. 
Произведение крайних членов пропорции будет равно произведению средних членов пропорции. 

Рассмотрим пример, когда пропорция может пригодиться в решении задач с процентами. 

Пример 1. В честь праздников магазин вводит на тортики скидку 15%. До скидок один тортик стоил 300 рублей. Сколько стоят тортики со скидкой? 

Решение. Пусть 300 рублей — это 100%, а х рублей — 15%. Если мы разделим 300 на 100  и разделим х на 15, то получим 1% от 300. Следовательно, можно составить пропорцию: 

\(\frac{300}{100} = \frac{x}{15}\). 

Решим полученную пропорцию: 

100 * x = 300 * 15
100 * x = 4500
x = 45

Получаем, что 15% от 300 будет равняться 45 руб.
Тогда, чтобы найти новую стоимость тортиков, необходимо из старой стоимости вычесть скидку: 
300 — 45 = 255.

Ответ: 255 рублей. 

Как увеличить процент

В решении задач нередко можно встретить формулировки “увеличилось на 25%” или “уменьшилось на 13%” и схожие с ними. Что значит увеличить число на процент? 

Разберем на примере: как увеличить сет роллов на 50%?
Предположим, компания друзей решили устроить вечеринку и заказали сет роллов. Спустя какое-то время они поняли, что одного сета на всех не хватает. Чтобы всем досталось роллов, им нужно взять еще половину такого же сета. 

Один сет – это 100%. А если мы добавим к нему еще половину такого же сета, то получим 100+50=150%. То есть мы к целому числу добавляем какой-то процент от него же. Это и есть увеличение числа на процент. 

Например, нам нужно увеличить число 160 на 15%. 15% от 160 будет равняться \(\frac{160}{100} * 15 = 1,6 * 15 = 24\).
Тогда, чтобы увеличить 160 на 15% нужно к 160 прибавить 15 процентов от него: 160 + 24 = 184.

Чтобы увеличить число а на r%, необходимо к этому числу прибавить r% от него.
\(а + \frac{r}{100} * a = a * (1 + \frac{r}{100})\)

Увеличим число 370 на 39%: 
\(370 + \frac{39}{100} * 370 = 370 (1 + \frac{39}{100}) = 370 * 1,39 = 514,3\).

Уменьшение числа на процент работает точно так же, но в обратную сторону. В этом случае наши друзья решат, что одного сета роллов на них очень много, поэтому нужно убрать половину от него. То есть они из 100% вычтут 50% и получат 50% роллов. 

Чтобы уменьшить число а на r %, необходимо из этого числа вычесть r % от него: 
\(а — \frac{r}{100} * a = a * (1 — \frac{r}{100})\).

Уменьшим число 670 на 41%:
\(670 — \frac{41}{100} * 670 = 670 * (1 — \frac{41}{100}) = 670 * 0,59 = 395,3\).

Выше мы рассмотрели начисление простых процентов: они начисляются только на изначальную сумму. 

Однако в экономических задачах встречаются и сложные проценты. 

Сложный процент — это процент, который со временем начисляется не только на изначальную сумму, но и на те проценты, которые были начислены до этого. 

Как смешать цвета и получить проценты? Рассмотрим сложные проценты как процесс смешивания  цветов. Например, смешали белый и синий и получили голубой.  Пусть белый — будет изначальное число, а синий — процент. Но потом оказалось, что оттенок получился недостаточно темный, поэтому еще раз добавили синий. В этот раз синий смешался уже не с чистым белым, а с голубым — то есть со смесью числа и процента.

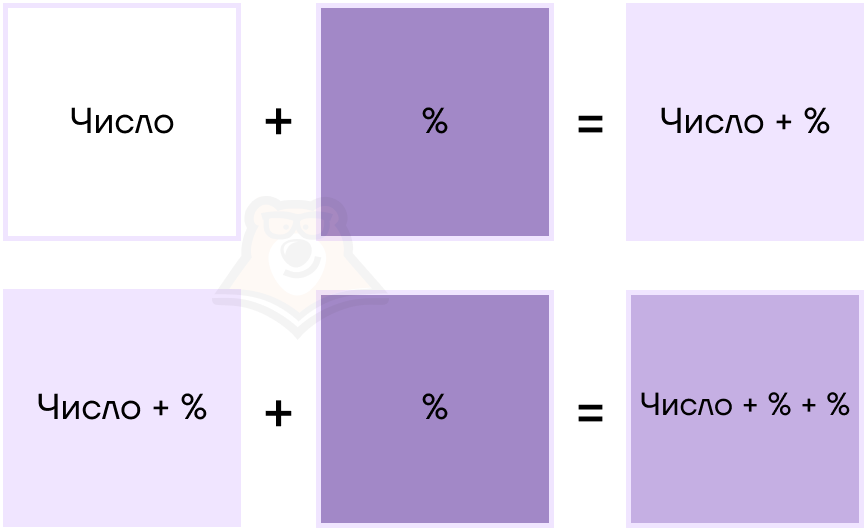
Обратимся к задаче. В банке был взят вклад S на 2 года под 25% годовых. Какая сумма будет на вкладе через два года? 

Каждый год сумма на вкладе будет увеличиваться на 25%.
Если мы увеличим S на 25%, то получим \(S + \frac{25}{100} * S =S(1 + \frac{25}{100}) = S * 1,25\). Следовательно, каждый год сумма будет увеличиваться в 1,25 раз.

Тогда в первый год мы получим 1,25S, а во второй год 1,25²S. 

Во второй год процент будет начислен не только на S, но и на 25% от S. 
Подробнее можно расписать так: 
1 год: \(S + \frac{25}{100} * S = S(1 + \frac{25}{100})\)
2 год: \((S + \frac{25}{100} * S) + (S + \frac{25}{100} * S) * \frac{25}{100} = (S + \frac{25}{100} * S)(1 + \frac{25}{100}) = S(1 + \frac{25}{100})(1 + \frac{25}{100}).\)

Следовательно, это будет сложный процент. 

Вклады

Проценты, в том числе увеличение числа на процент, очень часто применяется в решении задач на вклады. Разберем несколько примеров таких заданий. 

Но для начала определим, что такое банковский вклад?

Банковский вклад — сумма денег, которая передается банку и на которую ежегодно начисляются проценты. 

В банковских вкладах работает система сложного процента: ежегодно процент будет начисляться и на первоначальную сумму, и на проценты, начисленные ранее. 

Пример 1. Леша положил на вклад в банке 100 тысяч рублей под 10% годовых. Вклад был открыт на 4 года. После начисления процентов во 2 и 3 год Леша вносил равные дополнительные платежи. Чему были равны эти платежи, если через 4 года у Леши на вкладе оказалось 201,85 тысяч рублей?

Решение. Составим таблицу, с помощью которой проследим, как менялась сумма на вкладе с течением времени. 

Что может быть в таблице в задачах с банковскими вкладами:

• сумма на вкладе до начисления процентов;
• сумма на вкладе после начисления процентов;
• дополнительные платежи. 

Таблица может варьироваться в зависимости от задачи и отражать только актуальную информацию. 

Введем переменные. Пусть  S = 100 тысяч — первоначальный вклад, \(k = 1 + \frac{10}{100}\) — коэффициент увеличения, х — взносы в конце 2 и 3 года. 

Поскольку каждый год вклад увеличивается на определенное число процентов, намного удобнее будет ввести коэффициент увеличения, а не пользоваться выведенной ранее формулой. На самом деле, они не отличаются, просто коэффициент увеличения — это скобка, которая появляется при вынесении общего множителя. 

\(а + \frac{r}{100} * a = a * (1 + \frac{r}{100}) = a * k\)

1. Сразу составим таблицу на 4 года и заполним известные данные. Мы знаем, что в самом начале вклад был равен S, а дополнительные взносы в 2 и 3 год равны х. Заполним соответствующие ячейки. 

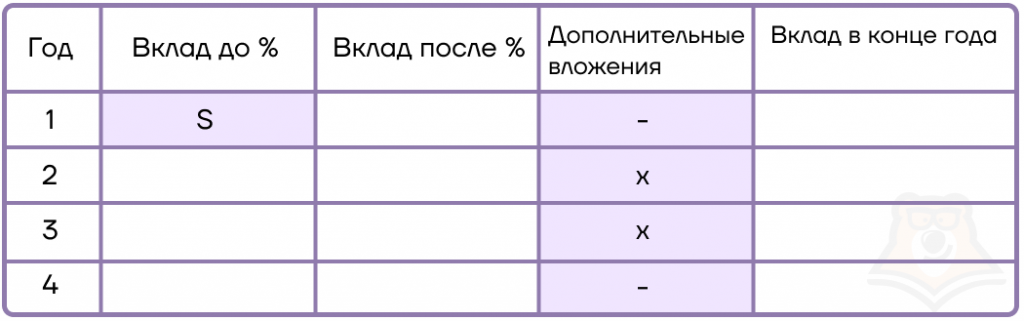
2. Дальше начислим процент на вклад. Пользуясь формулой, получаем: 

\(S + \frac{10}{100} * S = S(1 + \frac{10}{100}) = kS\). 

Поскольку в первый год дополнительных вложений не было, можем сразу заполнить и последнюю ячейку в первом году (просто перенесем данные из третьего столбика).

Заметим, что вклад в конце года и в начале следующего года одинаковый, поэтому сразу же можно будет переносить данные на следующую строчку. 

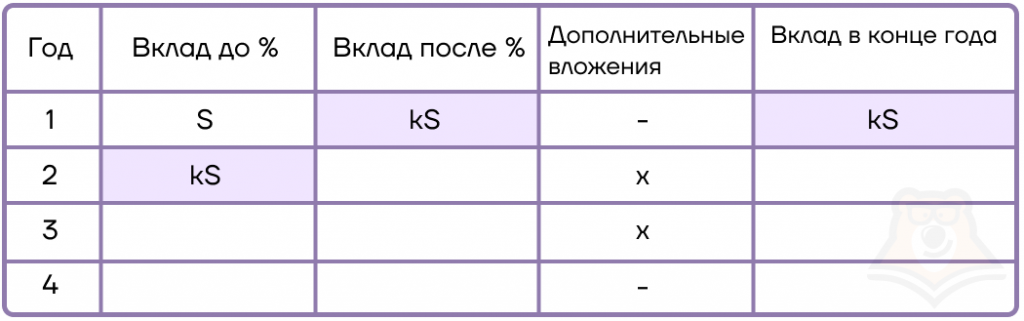
3. Дальше аналогично начисляем процент. Во второй год у нас уже есть дополнительные вложения. Чтобы получить вклад в конце года, необходимо сложить сумму вклада после начисления процентов и дополнительные вложения. 
Не забудем сразу перенести данные на начало третьего года. 

Оставшиеся два года заполняем по такому же алгоритму.

Таблица готова. 

4. По условию задачи вклад в конце четвертого года равен 201,85 тыс., поэтому мы можем составить уравнение:
 k⁴S + k²x + kx = 201,85

5. Теперь мы можем заменить переменные на известные величины:

1,1⁴ * 100 + 1,1²x + 1,1x = 201,85
146,41 + 1,21x + 1,1x = 201,85
2,31x = 55,44
x = 24 тыс. рублей. 

Ответ: 24 тыс. рублей

Пример 2. Маша хочет открыть вклад на 2 года, положив в банк целое число тысяч рублей.  В конце каждого года вклад увеличивается на 20%. В начале второго года Маша пополнила вклад на 25 тысяч рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 100 тысяч рублей. 

Решение. Пусть S – вклад, который хочет открыть Маша, \(k = 1 + \frac{20}{100} = 1,2\) – коэффициент увеличения, х = 25 – дополнительно вложение в начале второго года. 

1. Составим таблицу. 
Заметим, что в этой задаче проценты сразу будут начисляться и на дополнительные вложения, поскольку они сделаны в начале года 

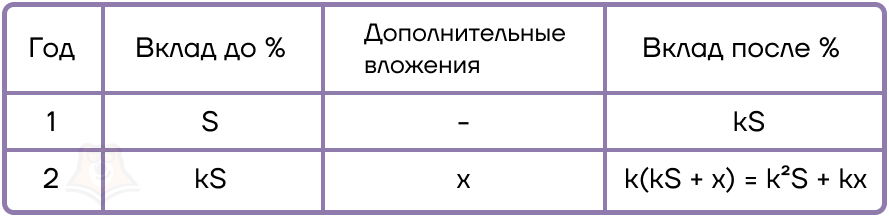
В конце расчетного периода вклад состоит из всех вложений, которые внесены на него, и процентов, начисленных на эти вложения. Следовательно, чтобы найти проценты, нужно из итоговой суммы вклада вычесть все вложения. 

2. Получаем неравенство: 
k²S + kx — (S + x) > 100

3. Подставим известные переменные и решим неравенство. 

1,2²S + 1,2 * 25 — S — 25 > 100
1,44S + 30 — S — 25 > 100
0,44 S > 95
\(S > \frac{95}{0,44}\)
\(S > \frac{9500}{44\)
\(S>\frac{44 * \frac{40}{44}\)

4. Поскольку S – целое число тысяч рублей, то ближайшее целое число, удовлетворяющее неравенству, будет S = 45. 

Ответ: 45.

Пример 3. По вкладу «Альфа» к концу года банк увеличивает на 20% сумму, имеющуюся на счете на начало года. По вкладу Бета банк увеличивает на 15% в первый и второй год, и на целое число r % в третий год сумму, имеющуюся на счете на начало года. Найдите наименьшее значение r, при котором за три года вклад Бета окажется выгоднее вклада Альфа, если на них внесли одинаковую сумму первоначальных взносов. 

Решение. Чтобы вклад Бета оказался выгоднее, через три года сумма на нем должна оказаться больше, чем через три года на вкладе Альфа. В этой задаче нам понадобится составить две таблицы: по одной для каждого вклада. 

1. Введем переменные. Пусть S — первоначальный взнос, \(k = 1 + \frac{20}{100} = 1,2\) — коэффициент увеличения для вклада Альфа, \(l = 1 + \frac{15}{100} = 1,15\) — коэффициент увеличения для вклада Бета в первые два года, \(x = 1 + \frac{r}{100}\) — коэффициент увеличения для вклада Бета в третий год. 

2. Составим таблицу для вклада Альфа. 

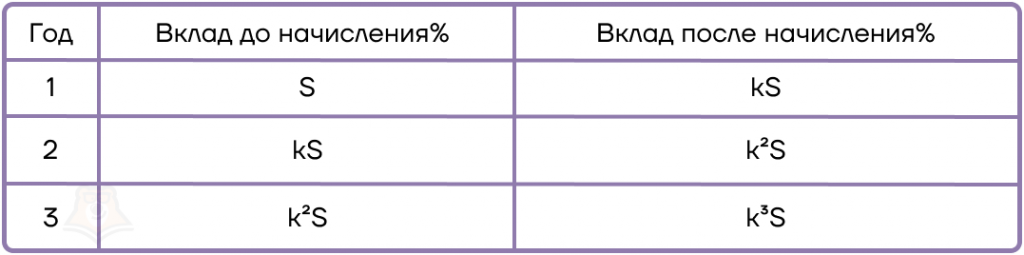
3. Составим таблицу для вклада Бета. 

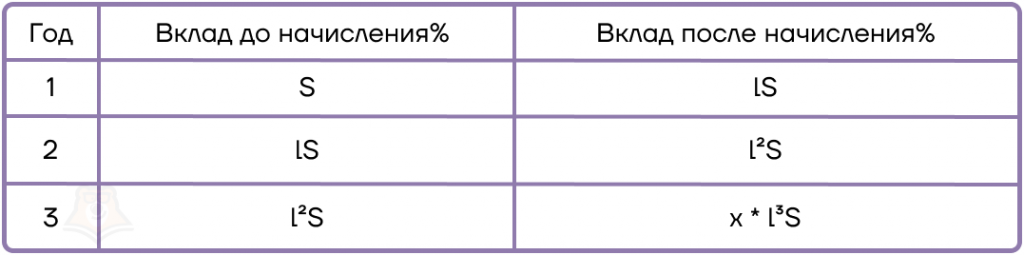
4. По условию должно получиться неравенство:
k³S < xl²S

5. Сократим S и подставим известные величины:

1,2³ < x * 1,15²
1,728 < 1,3225 x
\(x > \frac{1,728}{1,3225}\)
\(x > \frac{17280}{13225}\)
\(1 + \frac{r}{100} > \frac{17280}{13225}\)
\(\frac{r}{100} > \frac{4055}{13225}\)
\(r > \frac{405500}{13225}\)
\(r > 30\frac{8750}{13225}\)

6. По условию задачи r — целое число, а ближайшее минимальное целое число, удовлетворяющее неравенству r = 31. 

Ответ: 31

С помощью таблицы можно решить любую задачу, связанную с вкладами. А знание процентов может очень пригодиться в жизни, например, чтобы посчитать скидки. 

Фактчек

• Процент от числа — это одна сотая часть от него. Чтобы найти процент, необходимо число разделить на 100 равных частей, одна такая часть будет равняться 1% от числа. Эту операцию можно сделать в обратном порядке: если умножить 1% на 100, то получится первоначальное число. Процент также можно найти через пропорцию.
• Если необходимо увеличить или уменьшить число на определенный процент, то к этому числу нужно прибавить (вычесть) нужный процент от него.
• Банковский вклад — сумма денег, которая передается банку и на которую ежегодно начисляются проценты. В банковских вкладах работает система сложного процента: ежегодно процент будет начисляться и на первоначальную сумму, и на проценты, начисленные ранее. 
• Чтобы решать задачи на банковские вклады, достаточно правильно составить таблицу, и, уже опираясь на нее, получить итоговое уравнение или неравенство. 

Проверь себя

Задание 1.
Найдите 26% от числа 380.

1. 100
2. 98,8
3. 281,2
4. 26

Задание 2. 
Известно, что 100 – это 20% от какого-то числа. Найдите это число.

1. 20
2. 100
3. 5
4. 500

Задание 3. 
Магазин перед праздниками сделал скидку 11% на всю технику. В результате мультиварка стала стоить 3560 рублей. Сколько стоила мультиварка до скидок?

1. 4000
2. 3168,4
3. 3951,6
4. 4100

Задание 4. 
Что такое сложный процент?

1. Это процент, выраженный нецелым числом;
2. Это процент, который со временем начисляется не только на изначальную сумму, но и на те проценты, которые были начислены до этого. 
3. Это процент, который большее 100;
4. Ни один из приведенных выше вариантов. 

Задание 5. 
Число 200 уменьшили на 30%, а после этого полученный результат увеличили на 30%. Какое число получилось?

1. 140
2. 182
3. 200
4. 260

Ответы: 1. – 2 2. – 4 3. – 1 4. – 2 5. – 2