Интеграл

На этой странице вы узнаете:

• Как связаны Ньютон и Лейбниц?
• Почему площадь криволинейной трапеции считается через интеграл?

Интеграл

В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле? 

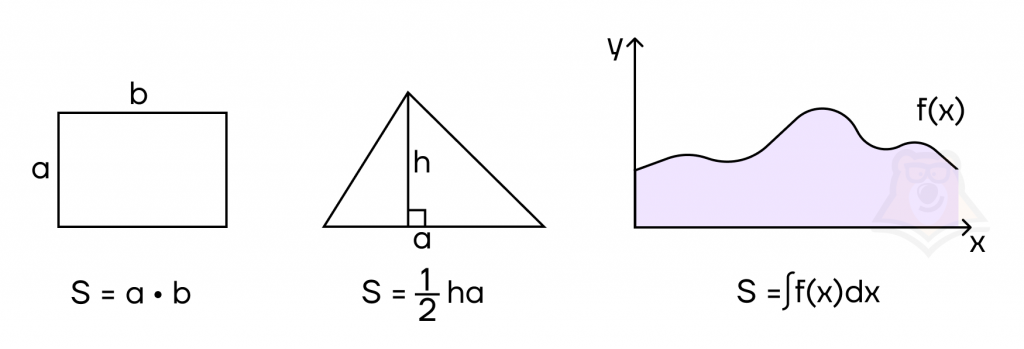
Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. Например, в геометрии есть формулы, чтобы посчитать площадь прямоугольника или треугольника, а если нужно посчитать площадь фигуры с кривой стороной, заданной функцией, поможет интеграл.

Если у функции y = f(x) есть первообразная y = F(x), тогда множество значений первообразных у = F(x) + С называют неопределенным интегралом функции y = f(x)

Записывается это следующим образом:

\(\int f(x)dx = F(x) + C\)

Какие бывают интегралы?

Интегралы бывают неопределенные и определенные.

Рассмотрим определенный интеграл. У такого интеграла в отличие от неопределенного есть предел интегрирования, то есть определённый отрезок.

Определенный интеграл функции на отрезке [a; b] – это приращение первообразных

Записывается это следующим образом:

\(\int\limits_a^b f(x)dx = F(b) — F(a)\)

Для данного интеграла пределом является отрезок от a до b

Как связаны Ньютон и Лейбниц? И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.

Формула Ньютона-Лейбница

Если функция f(x) непрерывна на промежутке [a; b], то 

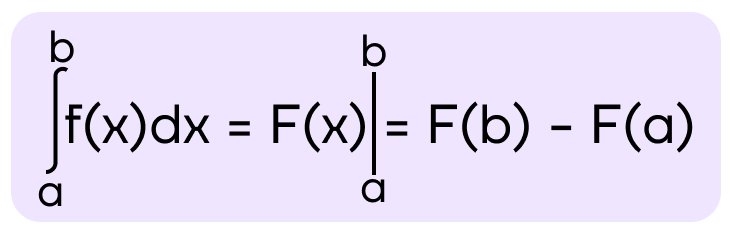
где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования, 
b – верхний предел интегрирования

Данная формула применяется для вычисления определенного интеграла

Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:

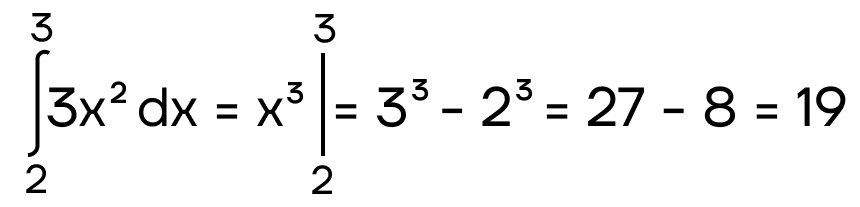
Интеграл для нахождения площади фигуры

Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b]. 

Нарисуем график.

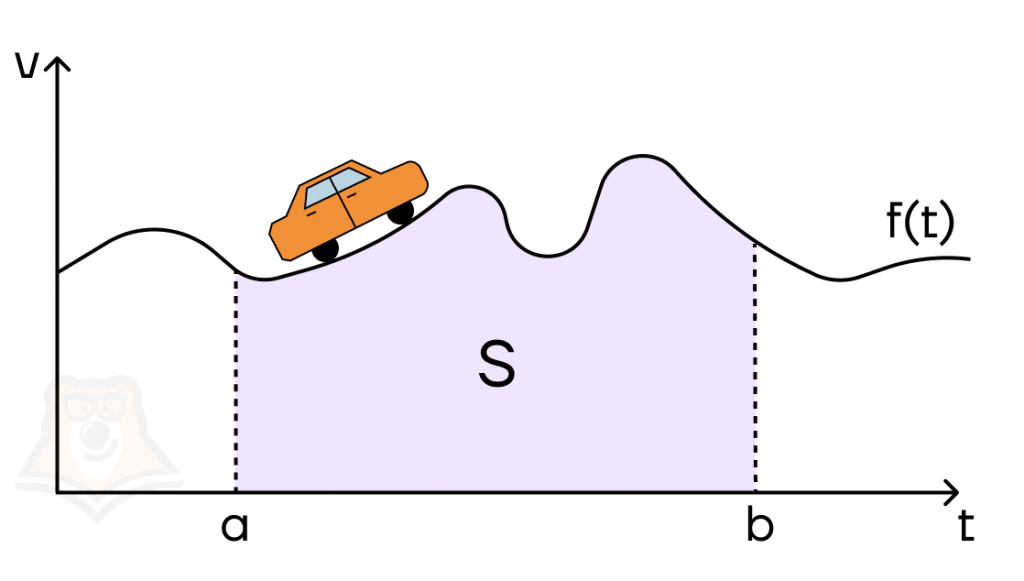
Скорость автомобиля V изменяется с течением времени, как f(t). Тогда, чтобы её найти, нам нужно посчитать площадь фигуры, ограниченной графиком функции f(t) на отрезке [a; b]. Такой фигурой будет являться криволинейная трапеция, а посчитать площадь можно с помощью интеграла. Далее мы подробно разберем, как это сделать.

Криволинейная трапеция – это фигура на плоскости, ограниченная графиком непрерывной функции на определенном отрезке, прямыми линиями и осью абсцисс.

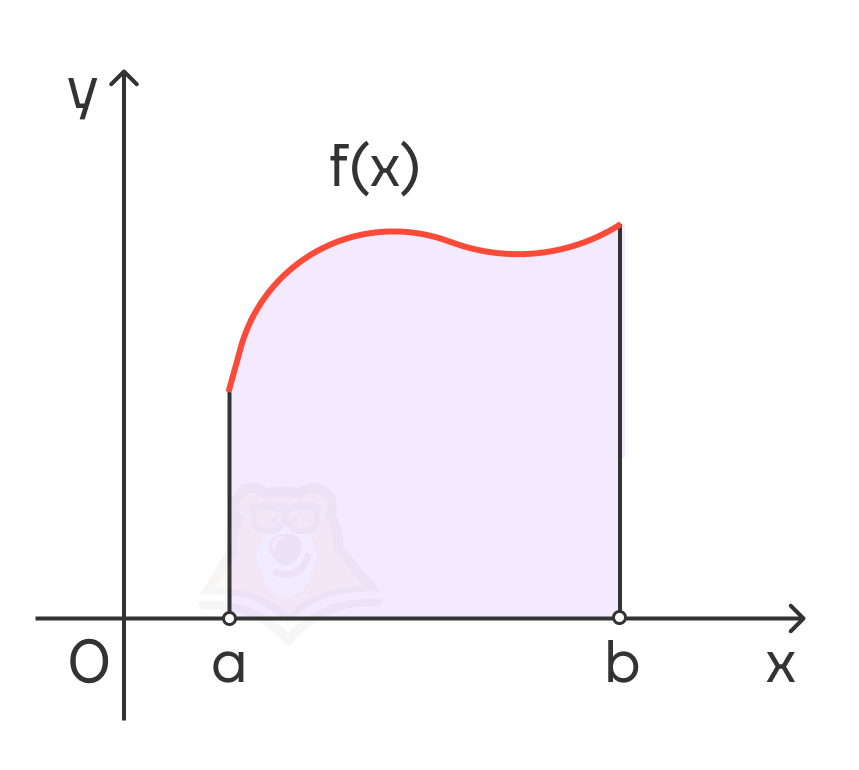
На данном рисунке фигура ограничена y = f(x), x = a, x = b, y = 0

Как найти площадь фигуры, используя интеграл?

Площадь такой фигуры, расположенной над осью абсцисс, можно посчитать, вычислив определённый интеграл по уже известной формуле Ньютона-Лейбница.

\(S = \int\limits_a^b f(x)dx\)

Почему площадь криволинейной трапеции считается через интеграл? Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов. 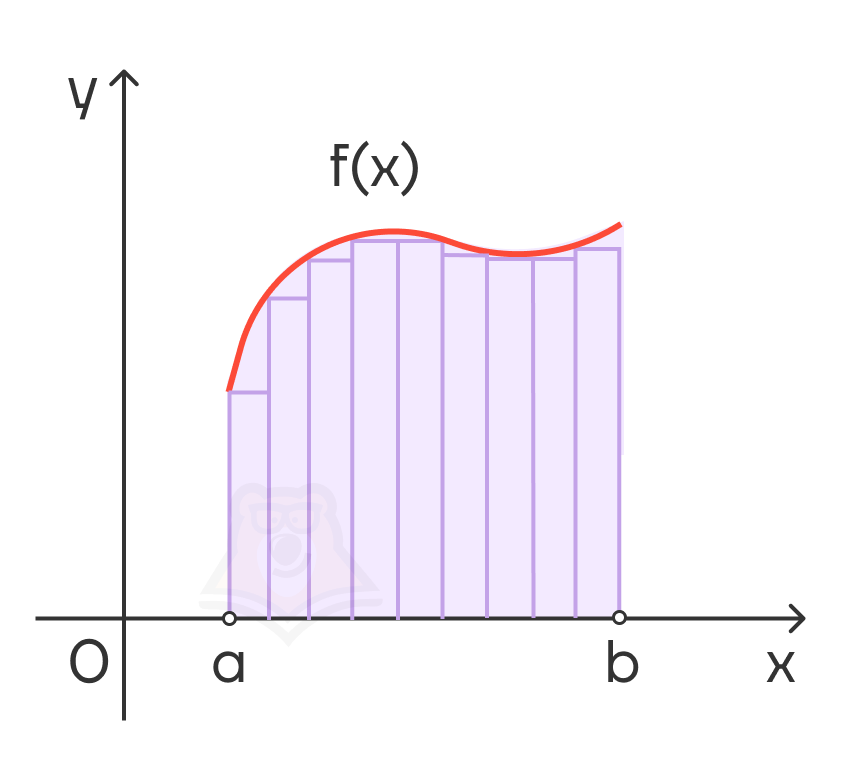 Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.  Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.  Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности. 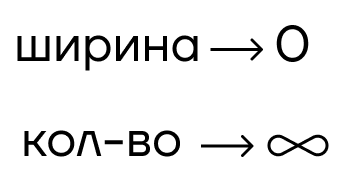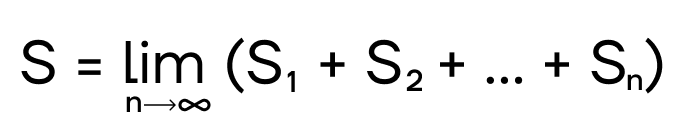При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом 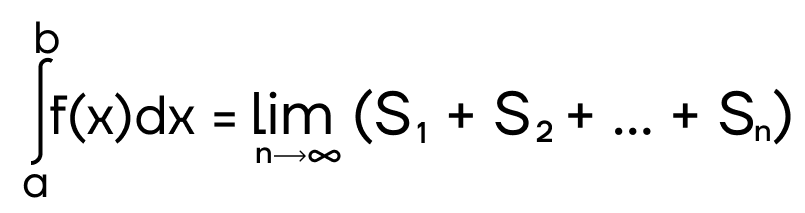, и равна какому-то числу.

А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле.

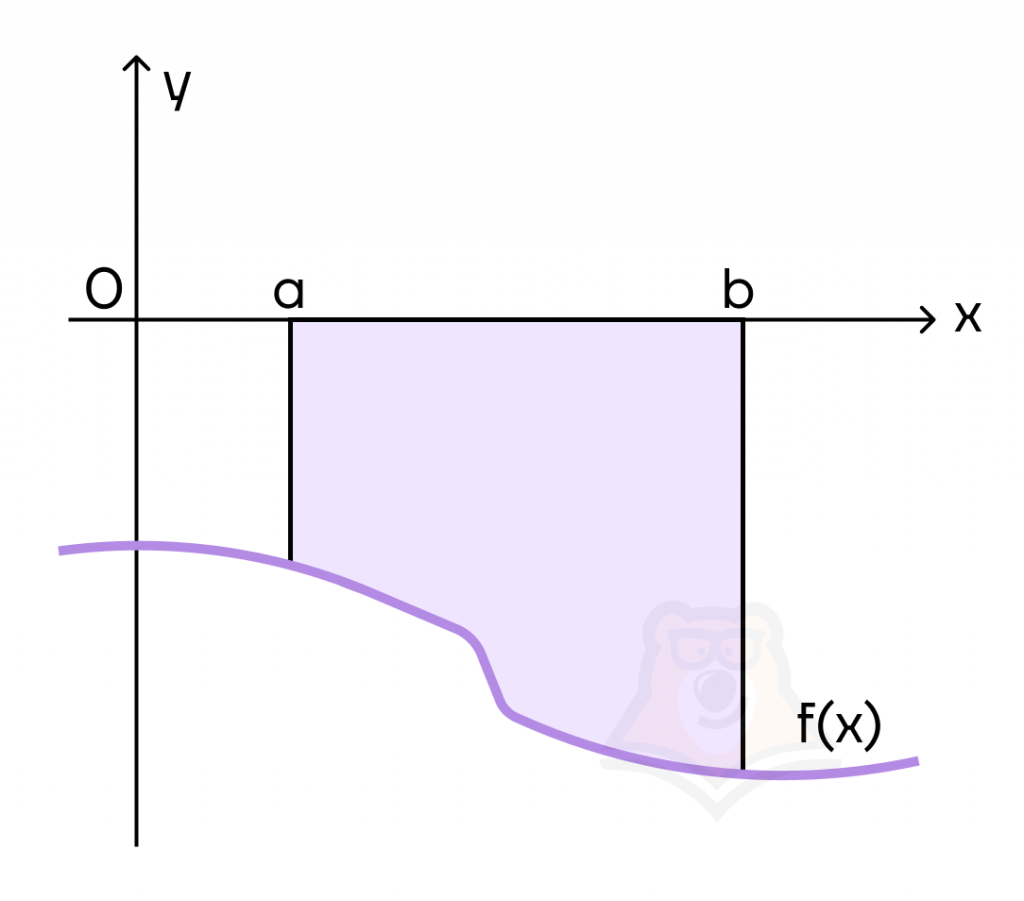
\(S = -\int\limits_a^b f(x)dx\)

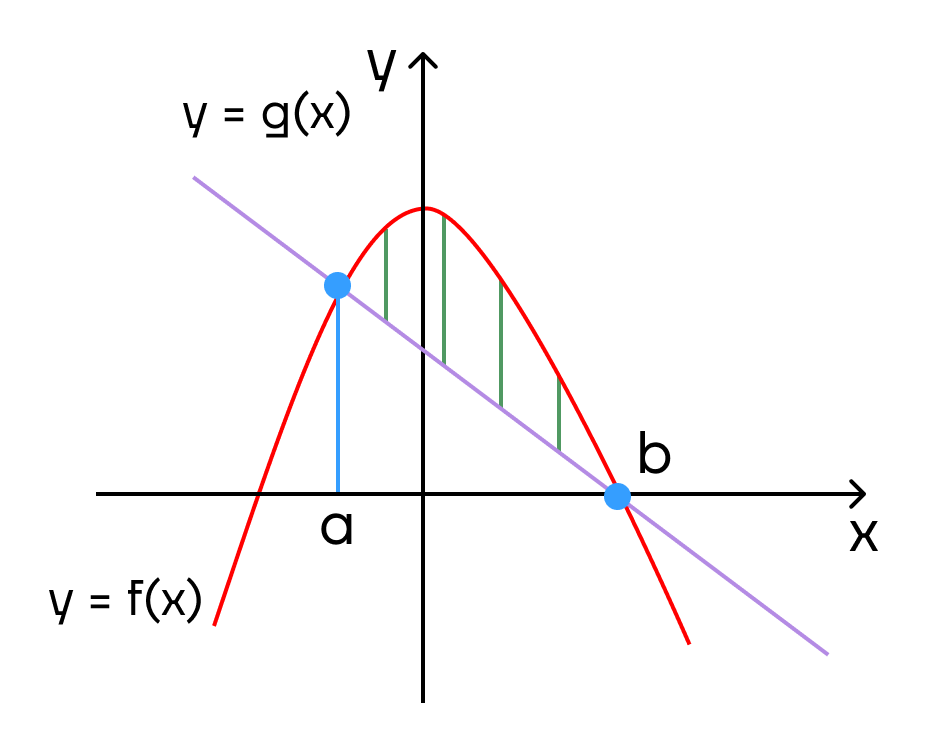
Если нужно найти площадь фигуры, ограниченной двумя функциями f(x) и g(x), то сначала данные функции приравниваются, так находится предел, а далее определяется функция, которая находится выше, и записывается формула

\(S = \int\limits_a^b (f(x) — g(x))dx\)

где f(x) – функция находящаяся выше
g(x) – функция находящаяся ниже
a и b – границы предела

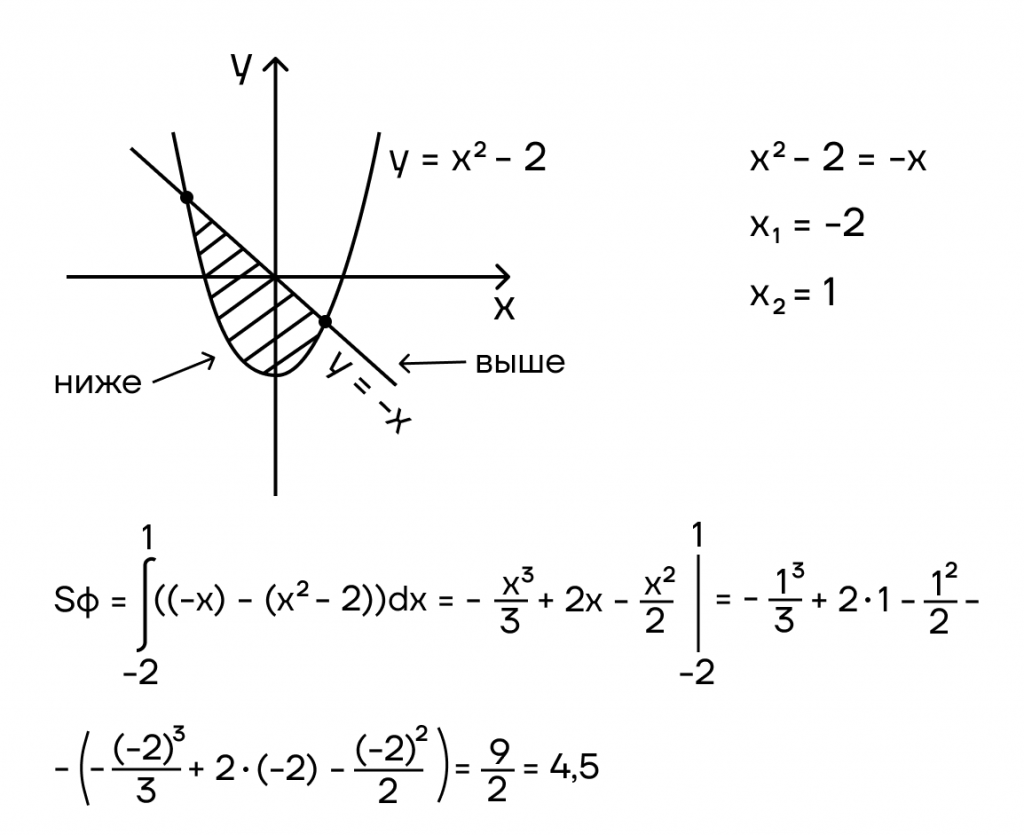
Пример:

Найти площадь фигуры ограниченной функциями y=x² — 2 и y = -x

Фактчек

• Интеграл — это площадь фигуры, находящейся под графиком функции.
• Неопределённый интеграл функции fx : \(\int f(x)dx = F(x) + C\)
• Определенный интеграл функции fx на отрезке [a; b] : \(\int\limits_a^b f(x)dx = F(b) — F(a)\)
• Формула Ньютона-Лейбница \(\int\limits_a^b f(x)dx = F(x) |_a^b = F(b) — F(a)\)
• Формула для нахождения криволинейной трапеции над осью х 
  \(S = \int\limits_a^b f(x)dx\)
• Формула для нахождения криволинейной трапеции под осью х
  \(S = -\int\limits_a^b f(x)dx\)
• Формула для нахождения площади фигуры, ограниченной двумя функциями
  \(S = \int\limits_a^b (f(x) — g(x))dx\), где 
  f(x) – функция находящаяся выше
  g(x) – функция находящаяся ниже

Проверь себя

Задание 1.
Найдите значение интеграла \(\int\limits_1^5 3dx\)

1. 3
2. 5
3. 12
4. 14

Задание 2.
Вычислите площадь фигуры ограниченной \(y = \sin x, x = 0,  x = \frac{\pi}{2}\)

1. 1
2. 0
3. 1,5
4. 2

Задание 3.
Вычислите площадь фигуры ограниченной y = 2x² — 5, x = -1,  x = 1

1. 9
2. \(8\frac{2}{3}\)
3. \(\frac{20}{3}\)
4. 8

Задание 4.
Вычислите площадь фигуры ограниченной y = x² — 3 и y = -2x² + 9

1. 32
2. 18
3. 24
4. 2

Ответы:  1. – 3; 2. – 1; 3. – 2; 4. – 1