Смешанные уравнения и неравенства

На этой странице вы узнаете

• В чем опасность смешанных уравнений и неравенств?
• Бывают ли чудеса в математике? 
• Как решить любое смешанное уравнение или неравенство? 

Рецепт смузи: почистить и порезать яблоко, банан и киви, сложить их в чашу блендера. Добавить мед и кефир. Перемешать.

И вот из, казалось бы, совершенно разных ингредиентов получается удивительно вкусный и полезный напиток! А всего-то нужно было их объединить вместе. 

На самом деле, в математике тоже существует свой «смузи». И он почти ничем не отличается от рецепта, приведенного выше: мы берем и смешиваем разные выражения. Но начнем по порядку. 

Смешанные уравнения

В математике существуют различные типы выражений, с которыми составляют уравнения и неравенства. Это и показательные, логарифмические и тригонометрические функции, это и дроби и даже корни. Именно они и служат «ингредиентами» для смешанных уравнений (и неравенств, о которых мы поговорим чуть позже). 

Смешанное уравнение – это уравнение, в котором одновременно присутствуют функции разных типов. 

Примерами смешанных уравнений могут быть:

\((\sqrt3sin(x)-2)(2x^2+7x-30)=0\)
\(log_5^2(tg x)-2log_5(tg x)-3=0\)
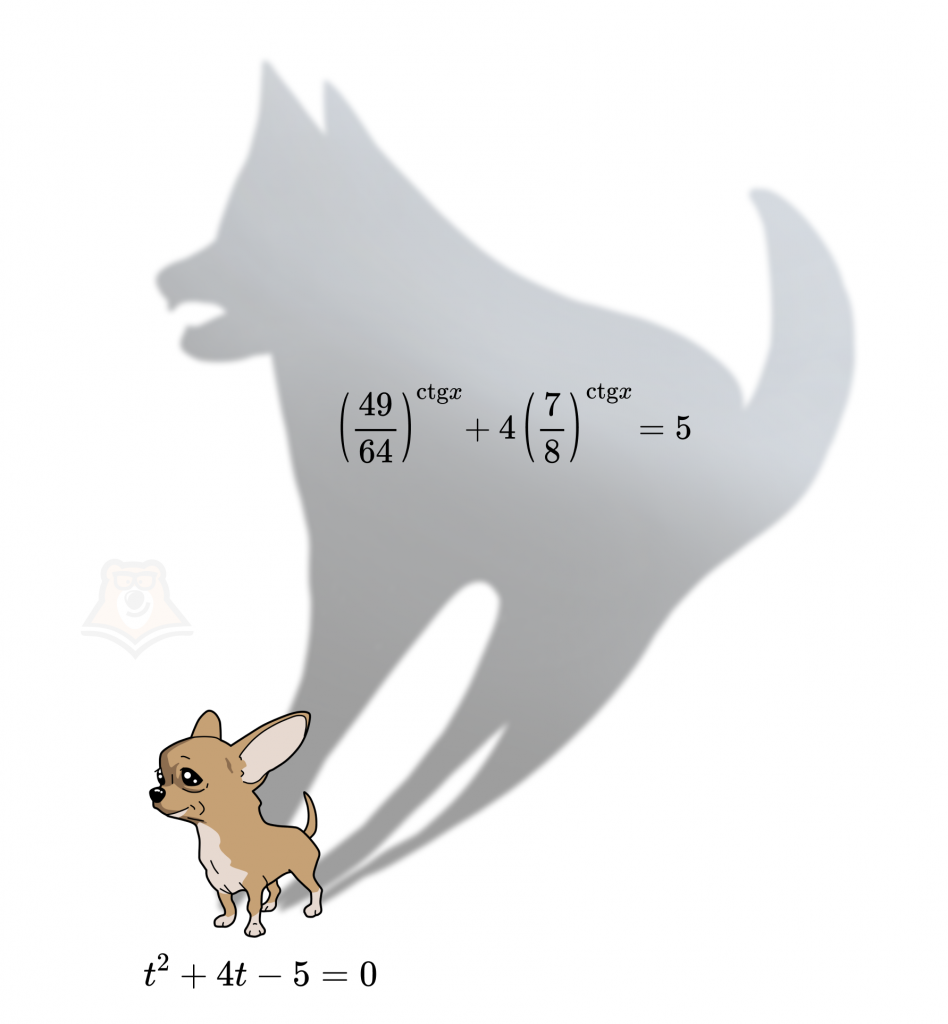
\((\frac{49}{64})^{ctg x}+4(\frac{7}{8})^{ctg x}=5\)

И, казалось бы, каждый из типов функций еще нужно научиться решать, а тут их еще и смешали, как с этим работать… Без паники! Смешанные уравнения, на самом деле, не сложнее обычных. Но у них есть одна особенность.

При решении смешанных уравнений нужно максимально их «упростить», то есть свести к наиболее простому выражению. 

К сожалению, смешанные уравнения не имеют четкого алгоритма решения: каждое из них решается по-разному. 

Их решение похоже на распаковку подарка, который упакован в несколько коробок: открываем одну, потом вторую, третью и так добираемся до ответа. 

Также и тут: мы будем просто «распаковывать» уравнение до тех пор, пока не получится наиболее удобное для решения выражение. 

А поскольку мы не можем вывести алгоритм, то сразу перейдем к практике! Решим один из примеров, который мы уже приводили ранее. 

Пример 1. \((\frac{49}{64})^{ctg x}+4(\frac{7}{8})^{ctg x}=5\).

Решение. Важно понять, что смешанные уравнения всегда хотят нас запутать и предстать в наиболее страшном виде. Попробуем немного преобразовать уравнение. 

Заметим что \(\frac{49}{64}=(\frac{7}{8})^2\). А значит, мы можем представить наше уравнение в виде:

\((\frac{7}{8})^{2ctg x}+4(\frac{7}{8})^{ctg x}=5\)

Теперь перенесем 5 влево:

\((\frac{7}{8})^{2ctg x}+4(\frac{7}{8})^{ctg x}-5=0\)

И сделаем замену. Подробнее про замены (или метод введения новой переменной) можно прочесть в статье «Тригонометрические уравнения». 

Пусть \(t=(\frac{7}{8})^{ctg x}\). Заметим, что \(t>0\), поскольку в какую бы степень мы ни возвели положительное число, оно останется положительным. Тогда уравнение принимает вид:

\(t^2+4t-5=0\)

А это уже обычное квадратное уравнение! Решим его с помощью дискриминанта. 

\(D=b^2-4ac=4^2-4*(-5)=16+20=36\)

\(t_1=\frac{-b+\sqrt{D}}{2a}=\frac{-4+6}{2}=1\)
\(t_2=\frac{-b-\sqrt{D}}{2a}=\frac{-4-6}{2}=-5\) – не удовлетворяет условию \(t>0\) 

Теперь сделаем обратную замену и преобразуем выражение по свойству степеней \(a^0=1\):

\((\frac{7}{8})^{ctg x}=1\)
\(ctg x=0\)

Теперь решим простейшее тригонометрическое уравнение: 

\(x=\frac{\pi}{2}+\pi n, n\in Z\)

Это и будет ответом нашего уравнения.

Ответ: \(x=\frac{\pi}{2}+\pi n, n\in Z\).

Итак, подведем небольшой итог. Чтобы решить смешанное уравнение, его нужно упростить и привести к другому типу уравнений, например, к квадратным. Как только уравнение упрощено, оно легко решается. 

Закрепим полученные знания на примере №12 из ЕГЭ по профильной математике.

Задание. а) Решите уравнение \(log_6(sin^2x+cos 2x-cos x+36)=2\).
б) Найдите все корни этого уравнения, принадлежащие отрезку \([\pi 5;\frac{13\pi}{2})\). 

Решение. а)Поскольку в уравнении дан логарифм, первым делом необходимо проверить его ограничения. Аргумент логарифма должен быть строго больше 0. 

Ограничения синуса и косинуса при этом: \(-1\leq sin x\leq 1\) и \(-1\leq cos x\leq 1\). А теперь посмотрим на аргумент. Если мы возьмем наименьшие значения для синусов и косинусов, то получим: \((-1)^2-1-1+36=35>0\). Иными словами, аргумент логарифма будет положителен при любых значениях х. 

Теперь перейдем к решению уравнения. Преобразуем логарифм по его определению: 

\(sin^2x+cos 2x-cos x+36=6^2\)
\(sin^2x+cos 2x-cos x+36=36\)
\(sin^2x+cos 2x-cos x+36-36=0\)
\(sin^2x+cos 2x-cos x=0\)

Раскроем косинус двойного угла:

\(sin^2x+(cos^2x-sin^2x)-cos x=0\)
\(cos^2x-cos x=0\)
\(cos x(cos x-1)=0\)

Если произведение множителей равно 0, то каждый множитель равен 0. Получаем два уравнения:

\(cos x=0\) и \(cos x-1=0\)

Решим первое:

\(cos x=0\)
\(x=\frac{\pi}{2}+\pi n, n\in Z\)

Второе уравнение:

\(cos x-1=0 => cos x=1\)
\(x=2\pi n, n\in Z\)

б) Найдем корни с помощью тригонометрической окружности:

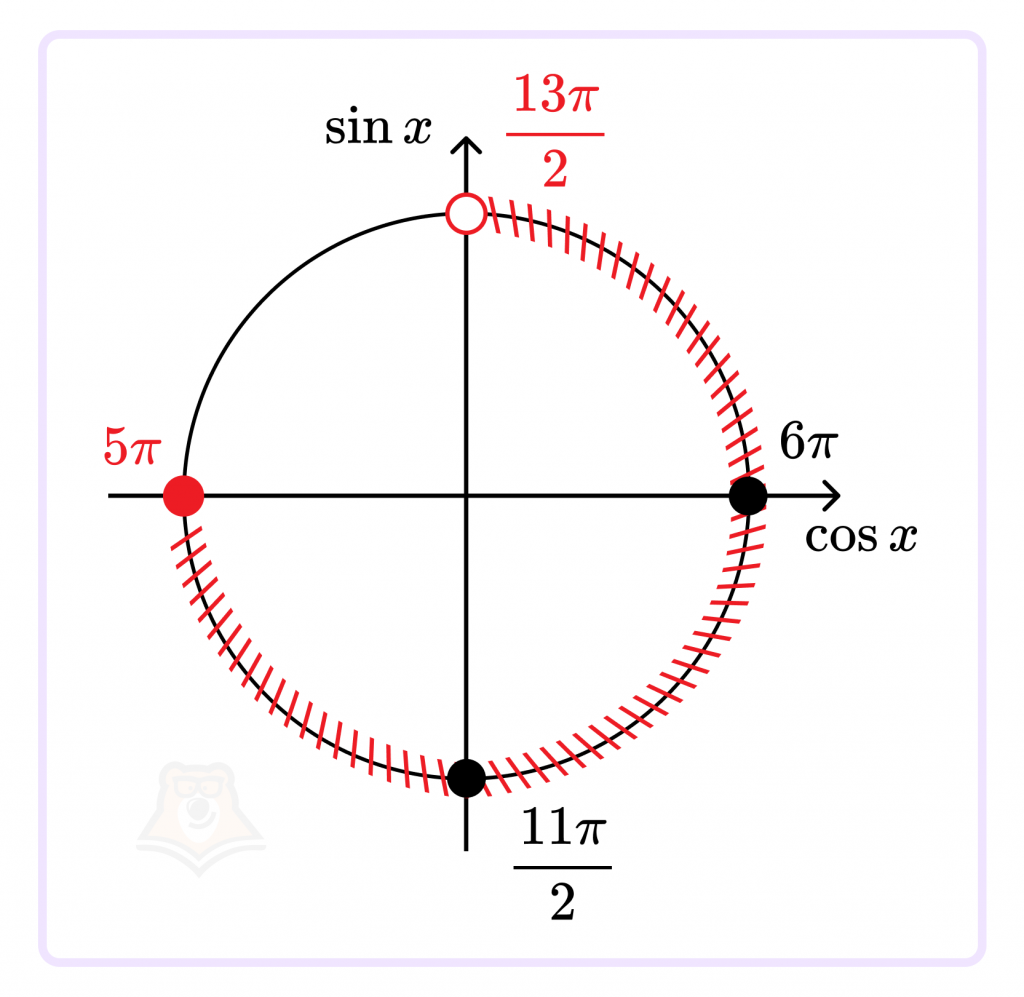
Ответ: а) \(x=\frac{\pi}{2}+\pi n, n\in Z, x=2\pi n, n\in Z\); б) \(\frac{11\pi}{2}; 6\pi \).

В чем опасность смешанных уравнений и неравенств?  Поскольку в таких выражениях могут встретиться сразу несколько функций, необходимо внимательно проверять ОДЗ для каждой из них. В ином случае, в ответе могут оказаться значения переменной, при которых выражение не будет существовать.

Мы разобрались в смешанных уравнениях, но что же делать с неравенствами?

Смешанные неравенства 

Определение смешанных неравенств не сильно отличается от уравнений. 

Смешанное неравенство – это неравенство, в котором одновременно присутствуют функции разных типов. 

Так же, как и с уравнениями, у них нет определенного алгоритма решения: каждое смешанное неравенство решается по-своему. Единственное общее, которое мы можем выделить в решении таких неравенств: как можно сильнее их упрощать до тех пор, пока неравенство можно будет легко решить. 

Поскольку принципиальной разницы между смешанными уравнениями и неравенствами нет, сразу перейдем к практике.

Пример 2. Решим неравенство \(\frac{log_{16}(4^x-1)}{x-0,5}>1\).

Решение. В неравенстве появляются логарифм и дробь, а значит, необходимо найти ОДЗ. 

ОДЗ логарифма: аргумент строго больше \(0\). Тогда \(4^x-1>0=>4^x>1\). По свойству степеней \(a^0=1\) получаем: \(4^x>4^0=>x>0\)

ОДЗ дроби: знаменатель не равен \(0\), тогда: \(x-0,5\neq 0=>x\neq 0,5\). 

Перейдем к решению неравенства. Перенесем все в левую часть и приведем к общему знаменателю:

\(\frac{log_{16}(4^x-1)}{x-0,5}-1>0\)
\(\frac{log_{16}(4^x-1)-(x-0,5)}{x-0,5}>0\)

Найдем нули функции. Для этого приравняем числитель и знаменатель к \(0\):
\(log_{16}(4^x-1)-(x-0,5)=0 и x-0,5\neq 0=>x\neq 0,5\) (в случае знаменателя ставим знак «не равно», поскольку знаменатель не может быть равен \(0\)). 

Решим уравнение для числителя:

\(log_{16}(4^x-1)-(x-0,5)=0\)
\(log_{16}(4^x-1)=x-0,5\)

По определению логарифма:

\(4^x-1=16^{x-0,5}\)

По свойству степеней \(a^{n-m}=\frac{a^n}{a^m}\):

\(4^x-1=\frac{16^x}{16^{0,5}}\)
\(4^x-1=\frac{16^x}{\sqrt{16}}\)
\(4^x-1=\frac{16^x}{4}|*4\)
\(4*4^x-4=16^x=>16^x-4*4^x+4=0\)

Заметим, что \((4^x)^2=4^{2x}=16^x\). Тогда сделаем замену \(t=4^x, t>0\) и получим:

\(t^2-4t+4=0\)

По формуле сокращенного умножения \((a-b)^2=a^2-2ab+b^2\) получаем:

\((t-2)^2=0\)
\(t=2\)

Сделаем обратную замену:

\(4^x=2=>x=0,5\)

Отметим на числовой прямой промежутки и расставим знаки, используя метод интервалов:

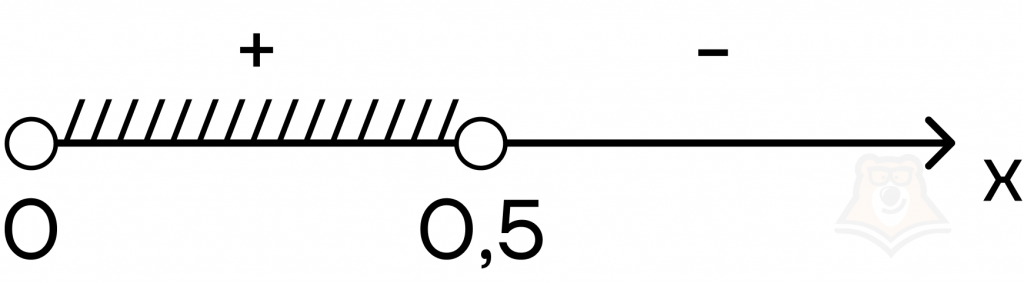
Ответ: (0;0,5). 

Несмотря на объем решения, неравенство свелось к обычному методу интервалов. В этом ли не прелесть математики: можно «раскрутить» любое выражение до той степени, что его легко становится решать. 

Бывают ли чудеса в математике? Если удариться в лирику, то решение смешанных уравнений и неравенств действительно похоже на чудо: мы берем «страшное» выражение и превращаем его в что-то совсем простое и легкое.  В математике такое «чудо» называется упрощением и применяется при решении любого выражения.

Разберем еще одно задание из ЕГЭ по профильной математике. В этот раз рассмотрим №14. 

Задание. Решите неравенство \(\frac{121^x+3*11^x-84}{11^x-21}\geq 1\).

Решение. Сделаем замену. Пусть \(t=11^x, t>0\). Тогда получаем неравенство:

\(\frac{t^2+3t-84}{t-21}\geq 1\)

Перенесем все слагаемые влево и приведем к общему знаменателю:

\(\frac{t^2+3t-84}{t-21}-1\geq 0\)
\(\frac{t^2+3t-84-(t-21)}{t-21}\geq 0\)
\(\frac{t^2+3t-84-t+21}{t-21}\geq 0\)
\(\frac{t^2+2t-63}{t-21}\geq 0\)

Решим неравенство методом интервалов. Найдем нули числителя:

\(t^2+2t-63=0\)
\(D=b^2-4ac=2^2-4*(-63)=4+252=256\)
\(t_1=\frac{-b+\sqrt{D}}{2a}=\frac{-2+\sqrt{256}}{2*1}=\frac{-2+16}{2}=7\)
\(t_2=\frac{-b-\sqrt{D}}{2a}=\frac{-2-\sqrt{256}}{2*1}=\frac{-2-16}{2}=-9\)

Нули знаменателя:

\(t-21\neq 0=>t\neq 21\)

Отметим точки на числовой прямой и расставим знаки:

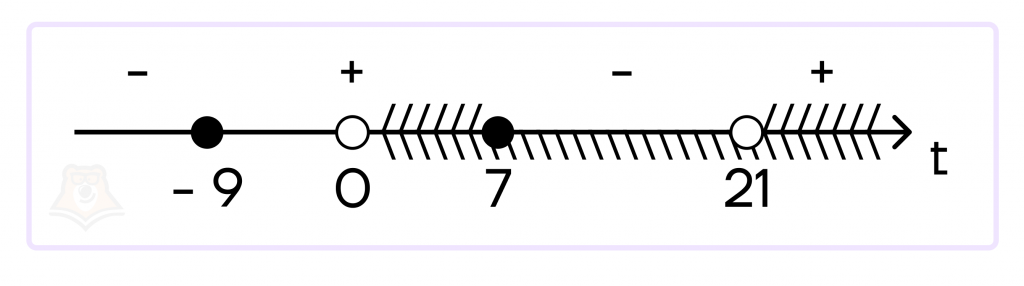
Получаем два промежутка:

\(0<t\leq 7\) и \(t>21\)

Сделаем обратную замену:

\(0<11^x\leq 7 => x\leq log_{11}7\) – тут мы не учитываем левую часть двойного неравенства, поскольку она просто показывает ограничение для показательной функции. 

\(11^x>21=>x>log_{11}21\).

Таким образом, мы получили в ответе: \(x\in (-\infty ; log_{11}7]\cup (log_{11}21;+\infty)\). 

Ответ: \(x\in (-\infty ; log_{11}7]\cup (log_{11}21;+\infty)\)

Как решить любое смешанное уравнение или неравенство? К сожалению, универсального совета или метода просто не существует. Как мы уже не раз упоминали в статье: каждое смешанное уравнение или неравенство решается по-своему. Но неужели тогда ничего нельзя сделать? Можно. Просто нужно практиковаться. Чем больше будет решено уравнений или неравенств такого типа, тем быстрее вы будете видеть пути и методы их преобразования, и в конечном счете вам будет достаточно одного взгляда на задание, чтобы понять, как его решать. Однако эта способность появляется только после того, как «набьется» рука, то есть будет решено огромное множество таких выражений.

Мы рассмотрели смешанные уравнения и неравенства. Однако примеры, которые мы рассмотрели – лишь малая часть таких заданий, которая существует. Поэтому рекомендуем самостоятельно закрепить результат, решив несколько смешанных уравнений и неравенств вне этой статьи. 

Мы не просто так решаем разные типы уравнений и неравенств: на их основе составляются математические модели для реальных ситуаций. А рассмотреть эти модели вы сможете в статье «Финансовые задачи».

Термины

Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле \(D=b^2-4⋅a⋅c\), где \(а, b\) и \(с\) берутся из уравнения.

Числовая прямая – прямая, на которой отмечены начало отсчета, шаг отсчета и положительное направление. 

Фактчек

• Смешанные уравнения и неравенства содержат в себе сразу несколько разных типов функций. 
• Каждое смешанное уравнение и неравенство решается по-своему, из-за чего нет четкого алгоритма решения таких заданий. Но есть схожая черта в их решении: необходимо максимально упрощать выражение и приводить его к простым уравнениям/неравенствам. 
• Нельзя забывать про ОДЗ или ограничения. Поскольку в смешанных уравнениях и неравенствах может быть сразу несколько функций, ограничения необходимо находить для каждой из них. 

Проверь себя

Задание 1.
Какое из уравнений является смешанным?

1. \(\frac{х}{2}+x^2=0\);
2. \(log_2x=log_2x^2\);
3. \(\frac{3^x}{2^x}=1,5\);
4. \(64^{sin x}-6*8^{sin x}-16=0\).

Задание 2.
Какое из утверждений верно?

1. В смешанном уравнении может быть только два типа функций. 
2. Существует универсальный метод решения смешанных уравнений.
3. Для решения смешанного уравнения его необходимо упростить. 
4. В смешанном уравнении нет необходимости искать ОДЗ. 

Задание 3.
Какое из утверждений верно?

1. Смешанное неравенство – это неравенство с несколькими переменными.
2. В смешанном неравенстве могут быть только нестрогие знаки неравенства. 
3. Смешанные неравенства невозможно решить.
4. В смешанном неравенстве обязательно будет несколько типов функций. 

Задание 4.
Решите неравенство: \(49^{lg x}-7^{lg x}-42<0\).

1. \(x<10\);
2. \(0\leq x<10\);
3. \(x>10\);
4. \(0<x<10\).

Ответы: 1. – 4; 2. – 3; 3. – 4; 4. – 4.