Работа с графиками функций

На этой странице вы узнаете 

• Что общего у падения с велосипеда и графиками?
• Каким способом еще, кроме графиков, можно представлять различные данные?
• Почему графики важны в мире инвестиций?

Как понять, почему одни товары стоят дороже, чем другие? Экономисты объясняют закономерность между стоимостью товара и его качеством с помощью зависимости одного от другого. Наглядно такую зависимость можно показать с помощью графика. 

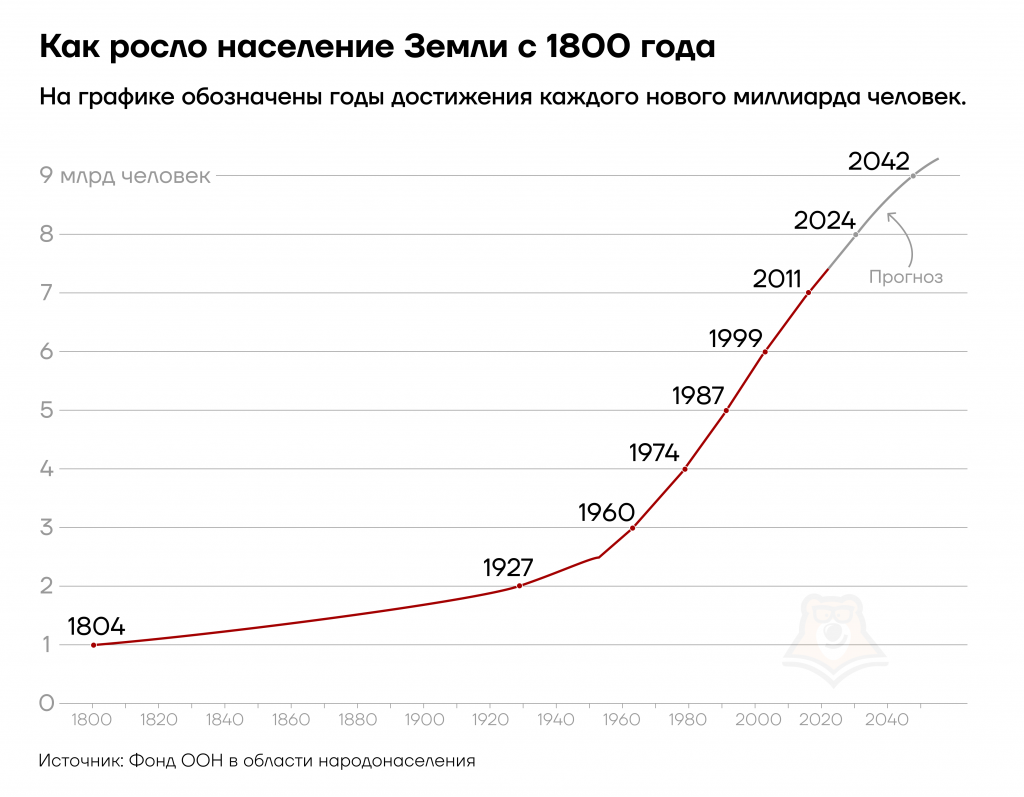
Различные виды зависимости описываются с помощью различных функций. Например, рост населения земли можно описать экспоненциальной зависимостью, то есть функцией \(y = e^x\).

Любые элементарные функции можно преобразовывать, то есть сжимать, растягивать или отражать. В реальном мире функции редко используются в своем исходном виде, преобразования нужны как раз для того, чтобы данный процесс был описан более приближенной к реальности функцией. 

Что общего у падения с велосипеда и графиками? При разработке искусственного интеллекта для управления велосипедом ученые из Калифорнии столкнулись с тем, что при управлении этим транспортом аварии могут происходить и по непредвиденным причинам, например, сильному ветру. Чтобы избежать падений, искусственный интеллект должен понимать, как действовать при тех или иных ситуациях, и какие движения необходимы, чтобы предотвратить «аварию». Для этого ученые 800 раз толкали велосипед, каждый раз он проезжал несколько метров и падал. А они по этим данным строили графики, вот что у них получилось. Анализ этого графика (и некоторых других инструментов) позволит искусственному интеллекту предотвратить падение, заранее распознав сценарий движения. В итоге ученые пришли к тому, что искусственный интеллект может вполне удачно управлять велосипедом, хотя и требует дальнейшей доработки. А подробнее узнать, почему искусственный интеллект так сложно научить, казалось бы, простой езде на велосипеде, можно тут.

Именно с тем, как преобразовывать графики функции, мы разберемся в этой статье. 

Преобразования графиков функции

Первый шаг в преобразовании любого графика – понимание, какую функцию вообще мы будем изменять. Вспомнить, какие функции бывают и как выглядят их графики, можно в наших статьях:

• «Основные элементарные функции. Часть 1»;
• «Основные элементарные функции. Часть 2».

При умножении или делении аргумента элементарной функции или даже самой функции на какое-то число исходный график видоизменяется, он может, например, растянуться или сжаться. Разберемся в этом подробнее. 

Симметричные преобразования

Если мы работаем с функциями, у которых в аргументе появляется -x или с функцией, которую можно задать как — \(f(x)\), мы сталкиваемся с ситуацией, когда наш график отражается зеркально относительно осей координат. Разберем отдельно каждый из случаев:

\(y = f(-x)\) – в такой ситуации происходит зеркальное отражение функции \(f(x)\) относительно оси \(Oy\). 

Разберем на примере: \(y = -x^3\)

Построим функцию \(f(x)=x^3\) и отразим симметрично оси \(Oy\).

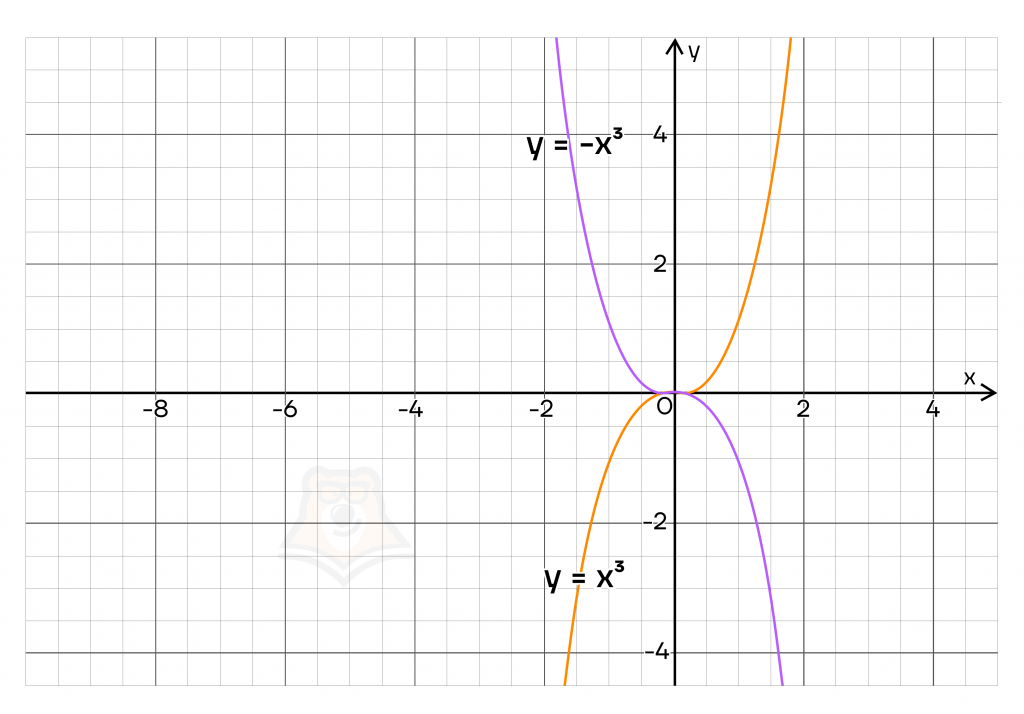
\(y=-f(x)\) – в данном случае отображаем зеркально относительно оси \(Ox\).

Например, \(y=-x^2\)

Построим функцию \(y=x^2\) и отразим симметрично оси \(Ox\).

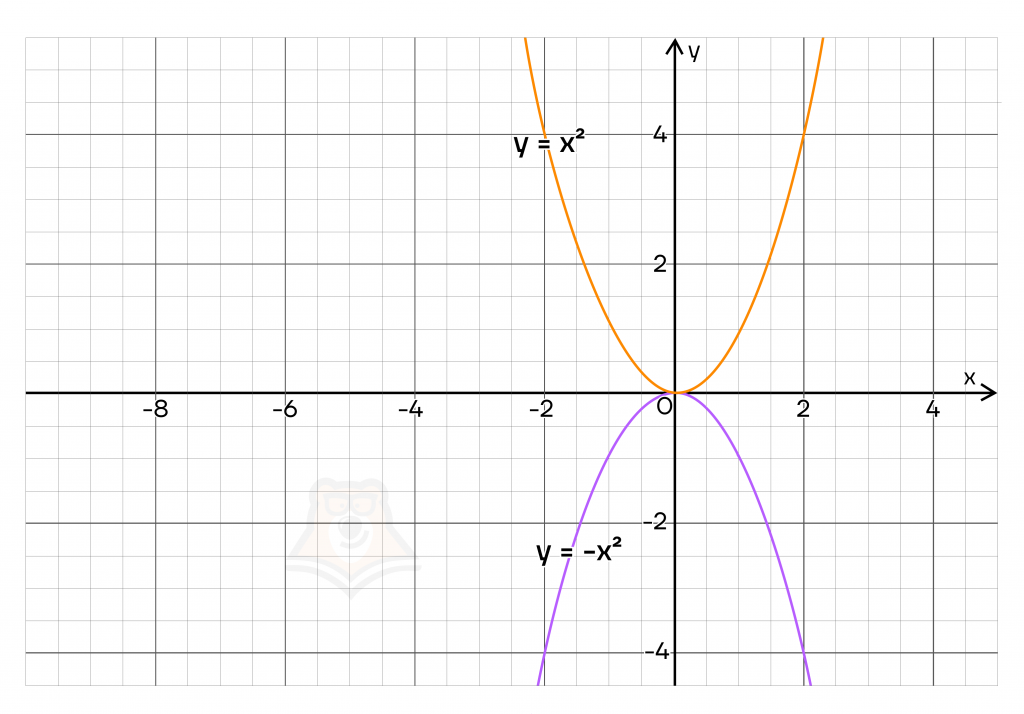
Разберем более сложные преобразования функции, которые с большой вероятностью могут встретиться на экзаменах.

Умножение или деление на константу

Умножение или деление аргумента функции на число – операция, при которой аргумент функции становится в какое-то количество раз больше или меньше исходного значения.

То есть изначально у нас есть какая-то функция \(f(x)\). При умножении ее аргумента на константу a, получим \(f(ax)\). При делении: \(f(\frac{x}{a})\).

Например, пусть \(f(x) = x^2+1\). Тогда \(f(ax)=(ax)^2+1=a^2x^2+1\), a \(f(\frac{x}{a})=(\frac{x}{a})^2+1=\frac{x^2}{a^2}+1\).

Как же меняется график функции, если мы делим или умножаем аргумент на число? 

— При умножении аргумента на число график сжимается вдоль оси абсцисс в a раз. 

— При делении аргумента на число график растягивается вдоль оси абсцисс в a раз.

При этом наибольшее и наименьшее значение графика по оси ординат никак не изменяется.5

Мы как будто бы фиксируем линейками полосу шириной с график, и внутри этой полосы мы можем его растягивать или сжимать.

Посмотрим, как это работает на примере: \(f(x) = sinx, a=2\). 

Тогда \(f(2x)=sin2x, f(\frac{x}{2})=sin(\frac{2}{x})\).

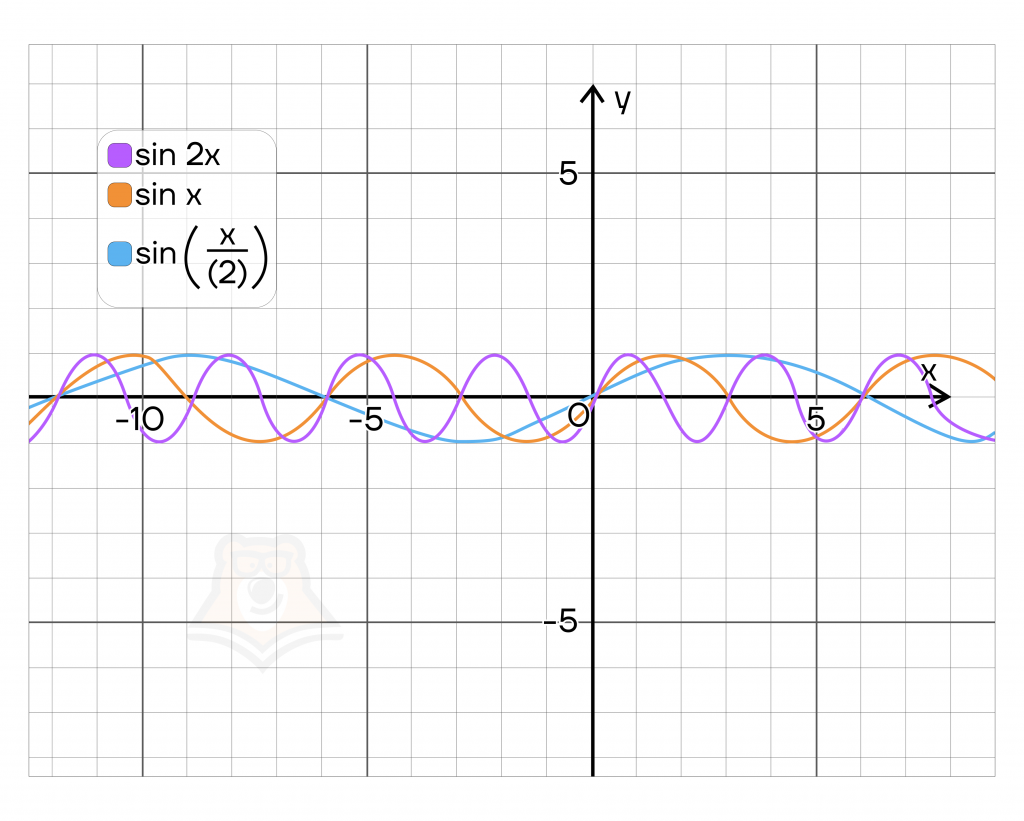
Умножение или деление функции на число – операция, при которой значении функции становится в какое-то количество раз больше или меньше исходного значения.

Изначально у нас есть какая-то функция \(f(x)\). При ее умножении на константу a, получим \(af(x)\). При делении: \(\frac{f(x)}{a}\).

Например, пусть \(f(x) = x^3+x+2\). Тогда
\(af(x)=a(x^3+x+2)=ax^3+ax+2a\) или
\(\frac{f(x)}{a}=\frac{1}{a}(x^3+x+2)=\frac{x^3}{a}+\frac{x}{a}+\frac{2}{a}\).

Что произойдет с графиком функции, если мы разделим или умножим ее на какое-то число?

— При умножении функции на число график растягивается вдоль оси ординат в a раз.

— При делении функции на число график сжимается вдоль оси ординат в a раз.

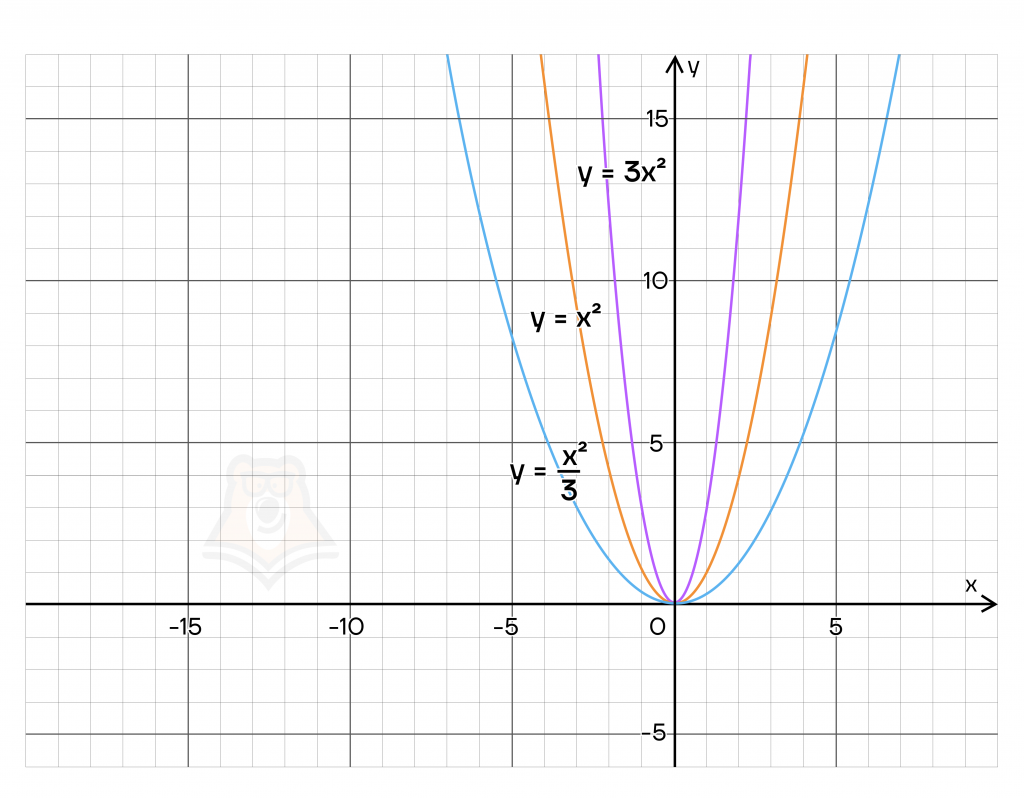
Разберем пример: \(f(x) = x^2, a=3\). 

Тогда \(3f(x)=3x^2, \frac{f(x)}{3}=\frac{x^2}{3}\).

Каким способом еще, кроме графиков, можно представлять различные данные? Различные данные, например распределение отличников, хорошистов и троечников в одном классе, можно представлять с помощью круговых диаграмм. Часто это даже более наглядное представление, чем графики. Кстати, данная диаграмма имеет кулинарные названия: например, в Англии ее называют «пироговой диаграммой», а во Франции – «диаграммой-камамбер».

Помимо сжатия и растягивания графика по вертикали и горизонтали, мы также можем сдвигать график функции влево, вправо, вверх или вниз. При этом сама функция никак не меняется, изменяется только ее положение относительно центра. Разберем это подробнее.

Сдвиг функции относительно начала координат

Добавление или вычитание числа из аргумента функции – операция, при которой аргумент функции увеличивается или уменьшается на какое-то число.

То есть у нас есть какая-то функция \(f(x)\). Прибавим к ее аргументу константу \(a\), получим \(f(x+a)\). Отнимем эту же константу: \(f(x-a)\).

Например, \(f(x)=sinx\). Тогда \(f(x+a)=sin(x+a); f(x-a)=sin(x-a)\).

Как меняется положение графика при добавлении или вычитании константы из аргумента? 

— При добавлении числа к аргументу функции график сдвигается влево (в отрицательную сторону) вдоль оси абсцисс на a делений.

— При вычитании числа из аргумента функции график сдвигается вправо (в положительную сторону) вдоль оси абсцисс на a делений.

Представьте раздвижную дверь шкафа, которая ездит в разные стороны при открывании и закрывании, вот также и наш график может перемещаться по оси x.

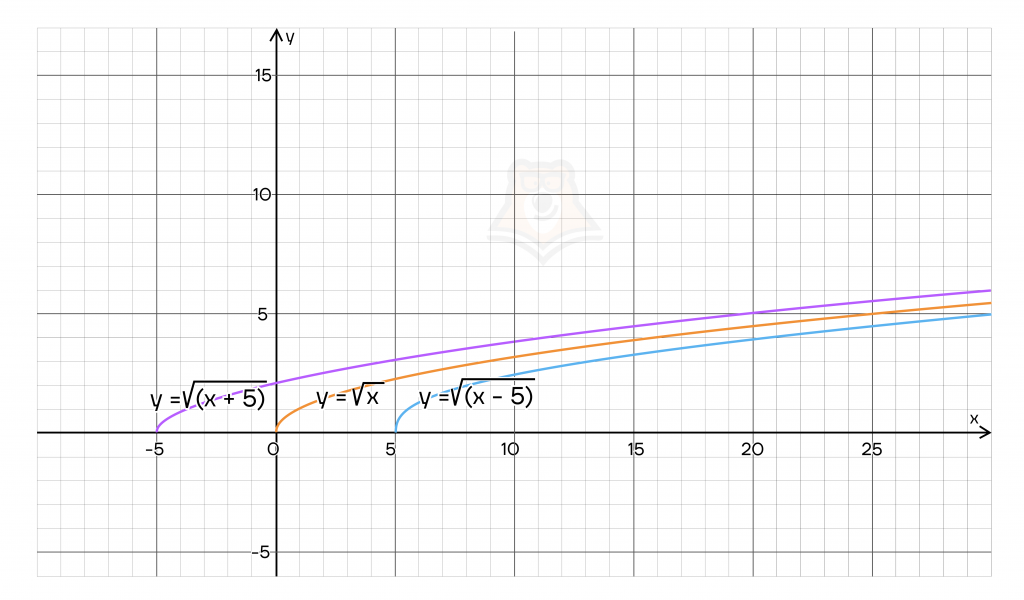
Разберем на примере: \(f(x) = \sqrt{x}. a=5\).

Построим \(f(x+5)=\sqrt{x+5}\) и \(f(x-5)=\sqrt{x-5}\).

Добавление или вычитание числа из функции – операция, при которой функция увеличивается или уменьшается на какое-то число.

Пусть у нас есть какая-то функция \(f(x)\). Прибавим к ней константу a, получим \(a+f(x)\). Отнимем эту же константу: \(f(x)-a\).

Например, \(f(x)=x^3\). Тогда \(f(x)+a=x^3+a; f(x)-a=x^3-a\).

Как меняется положение графика при добавлении или вычитании константы? 

— При добавлении числа к функции график сдвигается вверх (в положительную сторону) вдоль оси ординат на a делений.

— При вычитании числа из функции график сдвигается вниз (в отрицательную сторону) вдоль оси ординат на a делений.

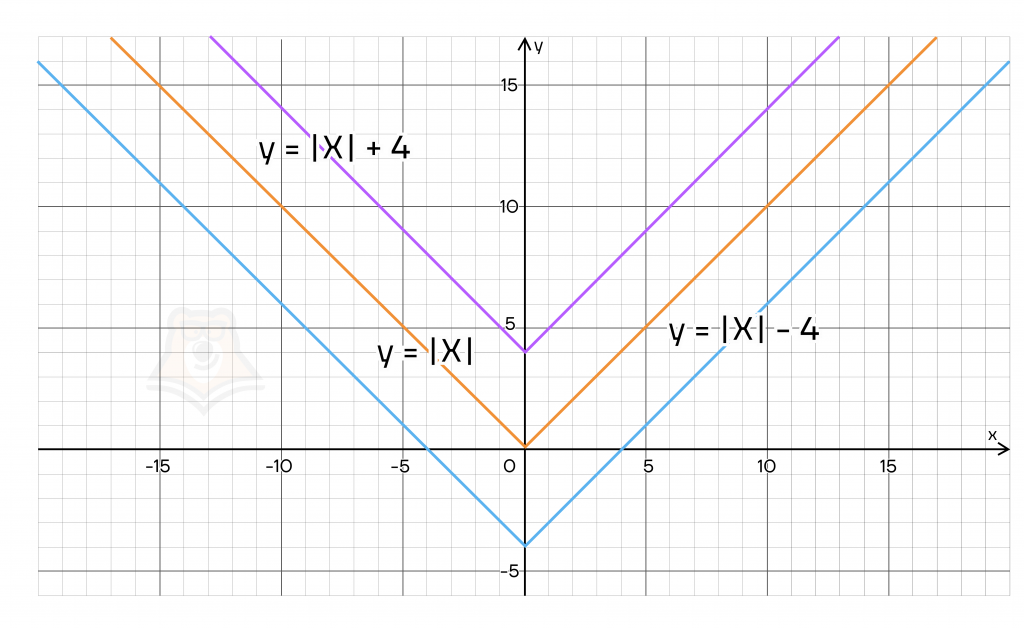
Например, \(f(x)=|x|, a = 4\).

Рассмотрим, как выглядят графики функции \(f(x)+4=|x|+4\) и \(f(x)-4=|x|-4\).

Уточним, что в ситуации переноса функции относительно системы координат, мы можем переносить не функцию, а исходную систему координат и уже в новой системе координат строить нашу функцию без учета сдвигов.

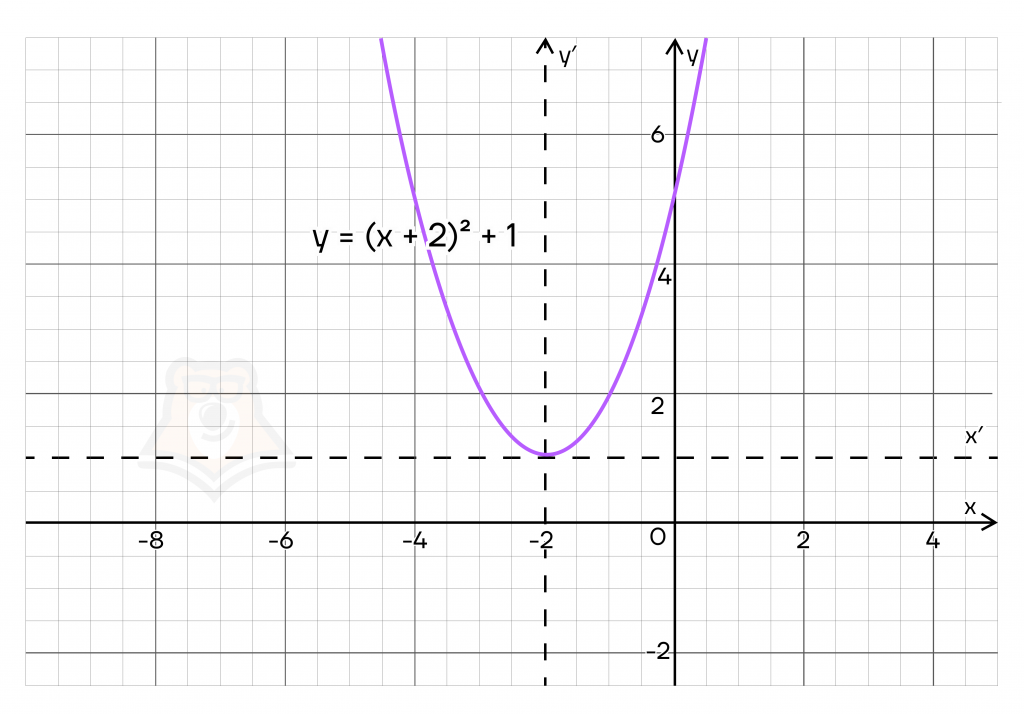
Например, \(y = (x+2)^2+1\)

Здесь мы видим сдвиг как по оси x на два деления влево, так и по оси y на одно деление вверх. Не будет сдвигать функцию, а перенесем сначала систему координат в точку (\(-2; 1\)).

И затем в этой системе координат построим функцию \(y = x^2\), то есть теперь мы уже не учитываем сдвиги. 

Все разобранные нами выше преобразования могут встретиться в задании № 22 ОГЭ по математике.

Задание. Постройте график функции \(y = 1+\frac{2(x+3)}{x^2+3x}\)  и определите, при каких значениях \(m\) прямая \(y=m\) не имеет с графиком ни одной общей точки.

Решение. Сначала найдем область допустимых значений аргумента исходной функции: 

\(x^2+3x ≠ 0\)
\(x(x+3) ≠ 0\)
\(x ≠ 0;-3\)

Теперь преобразуем график функции:

\(y = 1+\frac{2(x+3)}{x(x+3)}=1+\frac{2}{x}\)

Мы видим, что к функции \(y = \frac{2}{x}\) прибавляется число, равное единице. То есть здесь мы видим случай \(a+f(x)\), где \(a=1\).

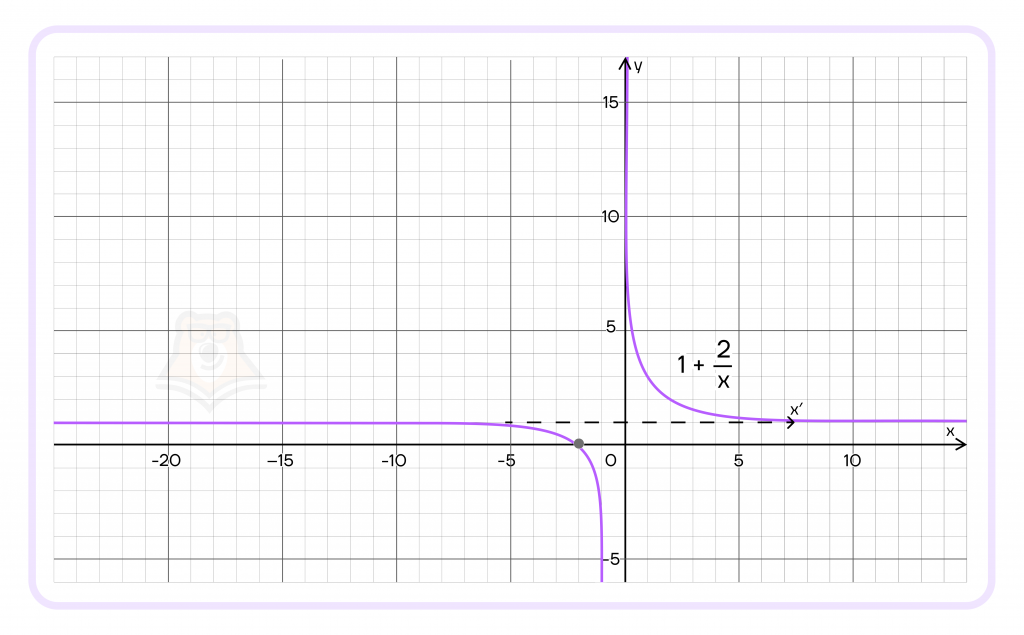
Перенесем систему координат в точку (0; 1) и в этой «новой» системе координат построим функцию \(y =\frac{2}{x}\).

Построим функцию \(y = \frac{2}{x}\) с помощью таблицы:

x	1	-1	2	-2
y	2	-2	1	-1

Кроме того, вспомним про нашу область допустимых значений \(x ≠ 0;-3\), значит, в этих точках нашей функции не существует, выколем точку \(x = 3\) на графике; при этом функция не равна \(0\), так как прямая \(x=0\) – асимптота нашей гиперболы.

Найдем прямую \(y =m\), которая не имеет ни одной точки пересечения с графиком.

Представьте, что вы ведете линейку от самой верхней точки графика до самой нижней точки, нужно найти положение, где нет пересечений.

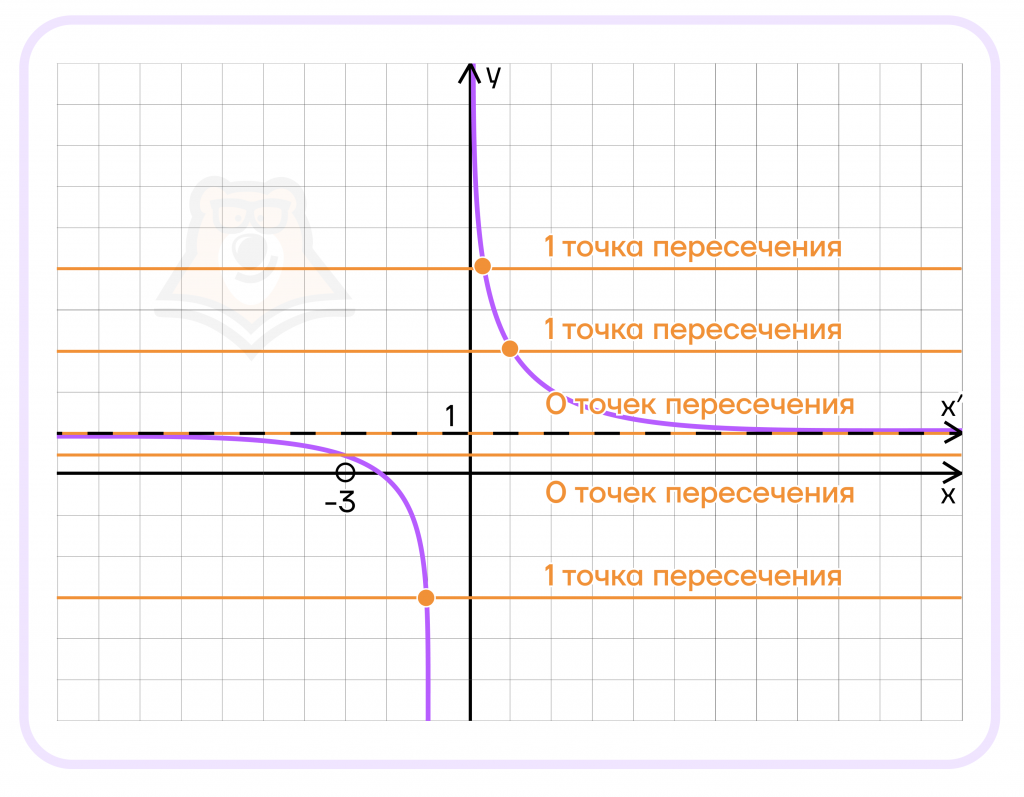
Нет пересечений на асимптоте, на «новой» оси x. Тогда \(y=1\).

Также нет пересечений в том случае, если функция \(y=m\) проходит через точку \(x=-3\), так как в этой точке как бы вообще нет графика, он там не может существовать.

Найдем значение \(y\), если \(x=-3\).
Подставим \(x=-3\) в уравнение гиперболы \(y=1+\frac{2}{x}\):  

\(y = 1+\frac{2}{-3}=1-\frac{2}{3}=\frac{1}{3}\). 

Ответ: 1; 13.

Кроме работы с исходным как-либо измененным графиком, мы можем столкнуться с графиками, в которых есть модуль. Иногда модуль можно раскрыть, но часто приходится работать с преобразованными графиками подмодульного выражения. 

Графики с модулем

Разберем сначала случай, когда у нас вся функция находится в модуле: \(|f(x)|\). 

Как строить график такой функции? Раскрывать модуль часто довольно сложно, например, если \(f(x)\) квадратное или кубическое выражение, поэтому нужно действовать по-другому. 

Алгоритм построения графика функции |f(x)|

1 шаг: Построить график подмодульного выражения, не обращая внимая на модуль.

2 шаг: Часть графика, находящуюся ниже оси абсцисс, отразить симметрично оси Ox в верхнюю полуплоскость системы координат. То есть мы должны как бы согнуть координатную плоскость по оси абсцисс и, таким образом, у нас получится исходный график |f(x)|.

Мы отражаем таким образом исходя из определения модуля: ведь модуль все отрицательные значения превращается в такие же, но уже со знаком плюс. Что мы и делаем, отражая отрицательную часть графика, на положительную полуплоскость.

Рассмотрим пример: \(f(x) =|x^2+4x-1|\)

Сначала строим график \(y=x^2+4x+1\).

А затем отражаем «хвостик», лежащий в отрицательной части, в верхнюю полуплоскость. И наш график построен! 

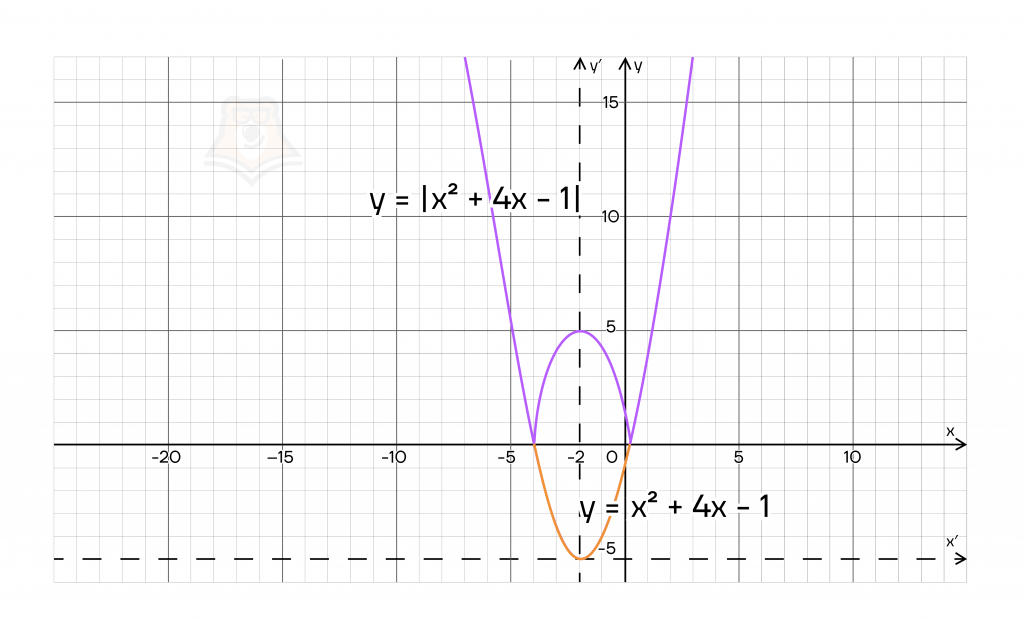
Второй вариант графика с модулем – функция, аргументом которой является \(|x|\). То есть мы будем работать с функцией \(f(|x|)\).

В данном случае раскрыть модуль уже вполне возможно, но мы рассмотрим другой вариант построения такого графика.

Алгоритм построения графика функции f(|x|)

1 шаг: Построить график исходной функции, убрав модуль у аргумента.

2 шаг: Часть графика, находящуюся правее оси ординат, отразить симметрично оси Oy в левую полуплоскость системы координат. То есть мы должны как бы согнуть координатную плоскость по оси ординат и, таким образом, у нас получится исходный график |f(x)|.

Например, \(f(x)=|x|+2\)

Строим график функции: \(y = x+2\)

А затем часть, лежащую в правой части системы координат, отразить относительно оси ординат:

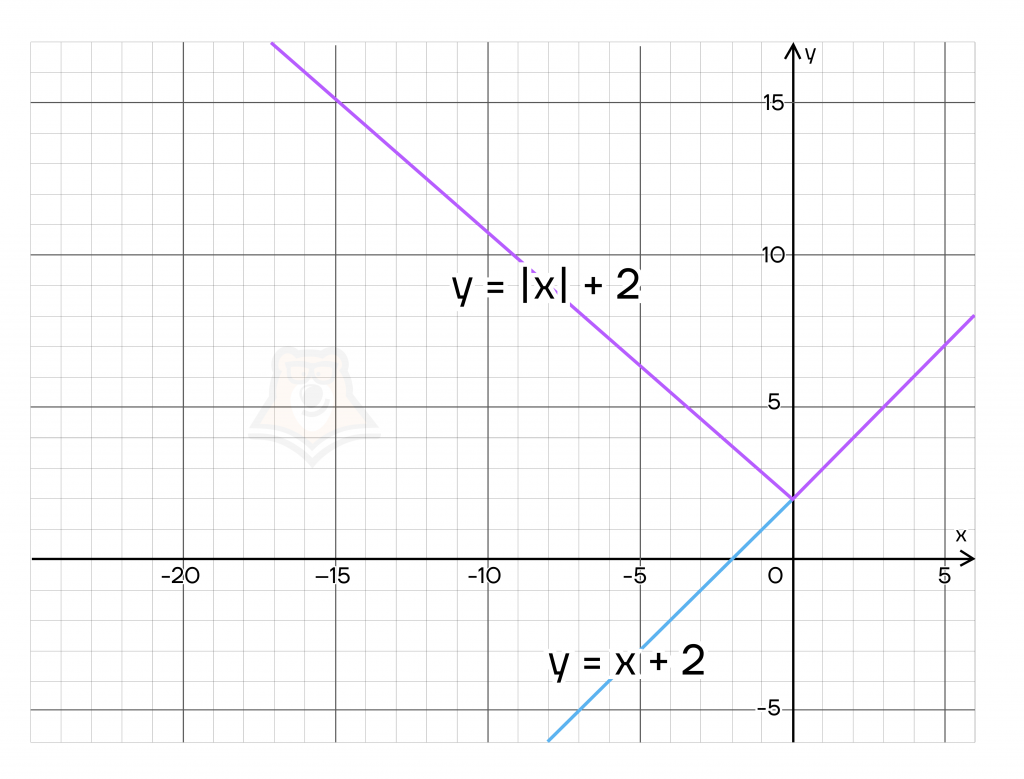
Подобные функции с модулем могут встретиться в ОГЭ по математике в задании №22.

Задание.Постройте график функции \(y = |x^2+2x-6|\) и определите, при каких значениях m прямая y=m имеет с графиком две общие точки.

Решение. Сначала построим график \(y =x^2+2x-6\)

Найдем координаты «новой» системы координат, найдя x вершины и y вершины.

\(x_0=\frac{-b}{2a}=\frac{-2}{2}=-1\)

Найдем \(y_0\), подставив \(x_0\) в уравнение параболы:

\(y_0=(x_0)^2+2x_0-6=(-1)^2+2*(-1)-6=1-2-6=-7\)

Перенесем центр системы координат в точку вершины параболы (\(-1; -7\)), в «новой» системе координат строим график \(y=x^2\).

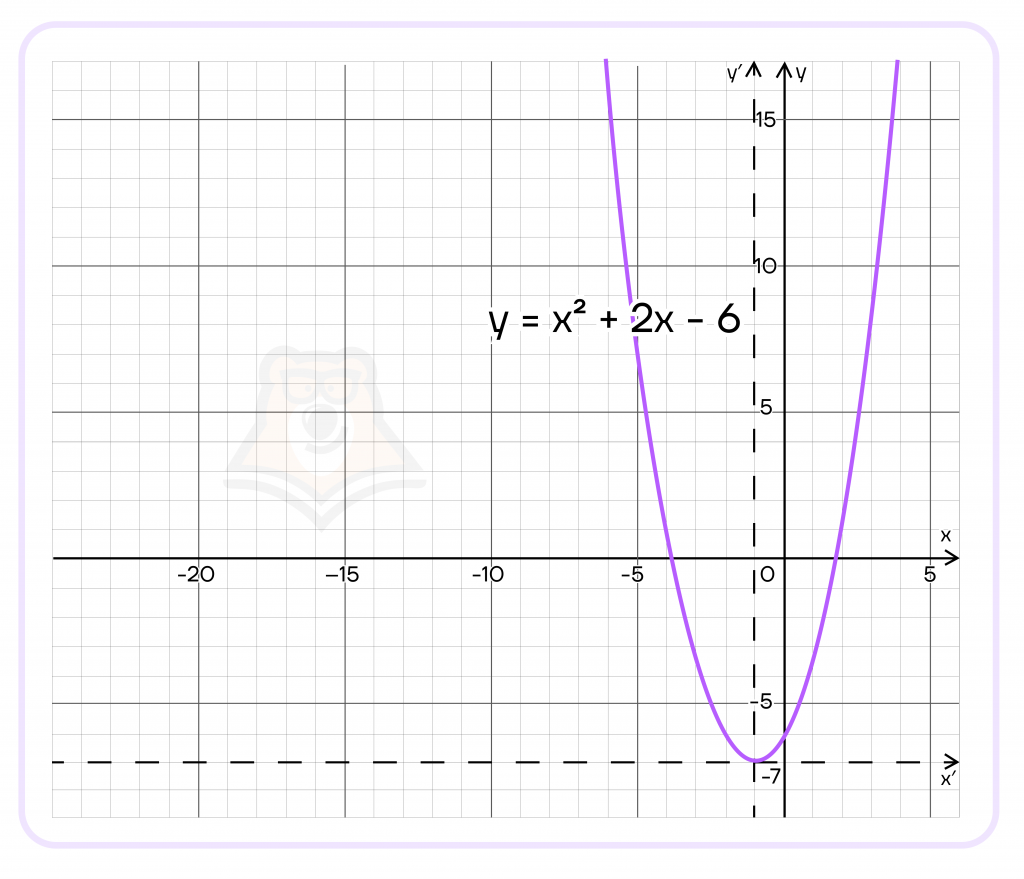
Отразим теперь часть графика, лежащую ниже оси ординат, в верхнюю полуплоскость.

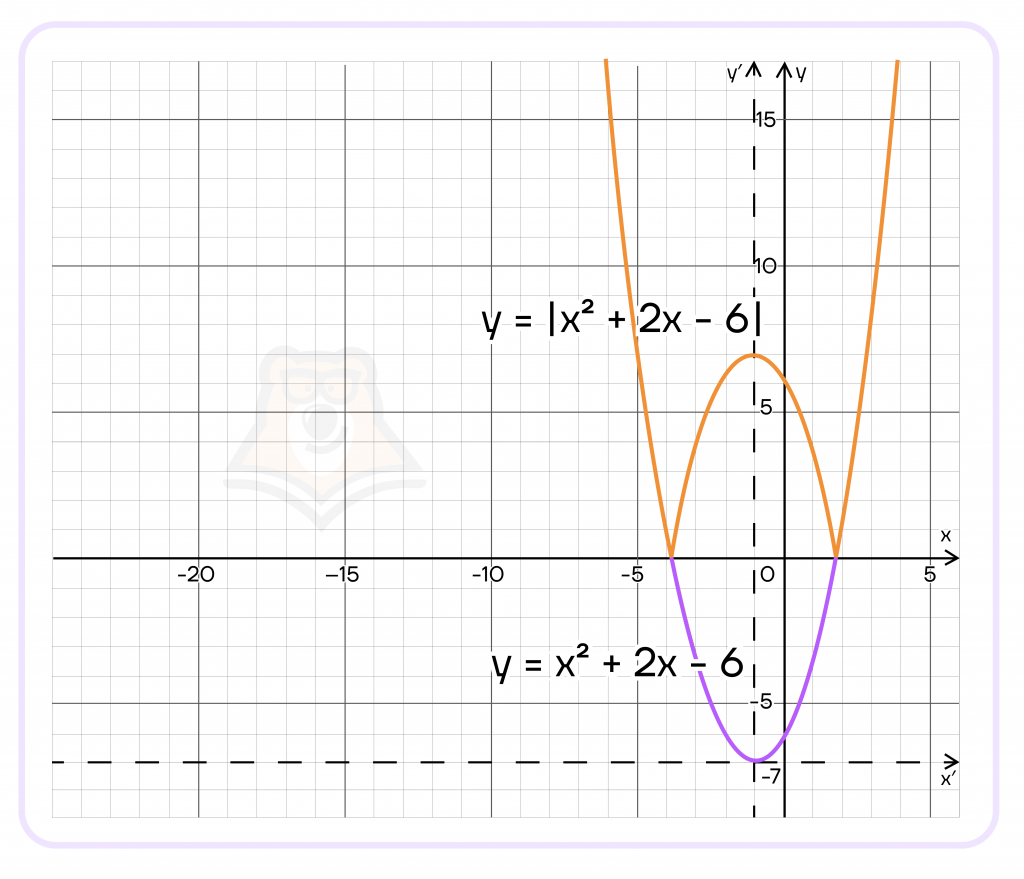
Найдем теперь такие m, при которых прямая \(y=m\) имеет с графиком две общие точки, будет также представлять, что мы ведем линейку по графику функции.

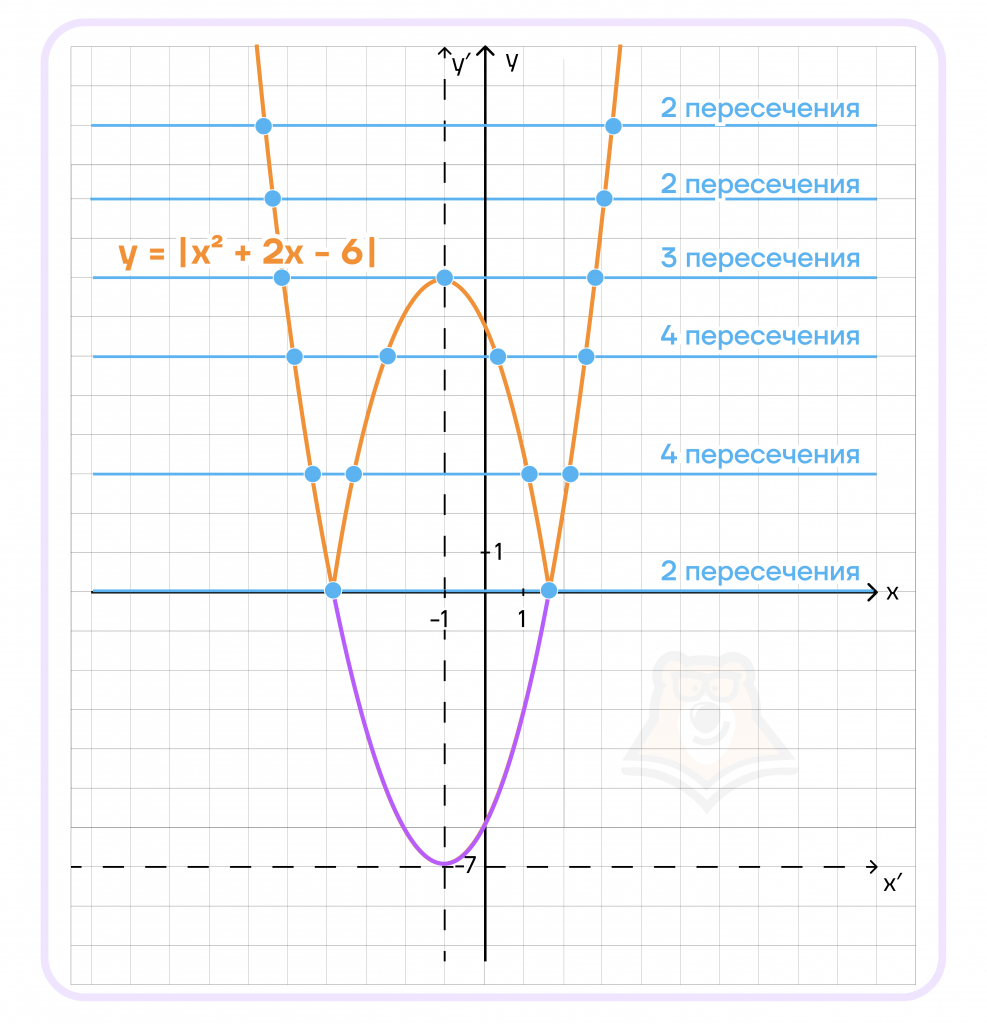
Мы видим, что у графика \(y=m\) и у исходной функции две точки пересечения в том случае, когда \(m=0\), а также когда \(m>7\).
Ответ. {\(0\)}\(\cup(7;+\infty)\).

Мы разобрали преобразования графиков функций, дальше поговорим об обратных функциях.

Обратные функции

Обратная функция — это функция, которая возвращает исходное значение, для которого функция дала выход. 

Обратные функции обычно обозначают как \(f^{-1}(x)\).

Представьте, что вы видите салат. Вы можете точно сказать, из чего он приготовлен, например, помидоры, огурцы и зелень. А как насчет количества ингредиентов? Тут остается только гадать или предполагать приблизительное число, то есть появляется несколько вариантов. 

Похожая ситуация происходит в работе с функциями: например, у линейной функции, зная значение ординаты \(y\), можно точно и однозначно узнать значение \(x\). С параболой же так не получится: одно значение \(y\) может дать несколько разных значений \(x\).

Такие рассуждения подводят нас к обратным функциям: обратная функция обращает данную нам зависимость, то есть исходная функция показывает зависимость \(y\) от \(x\), тогда обратная функция покажет нам, как наоборот \(x\) зависит от \(y\).

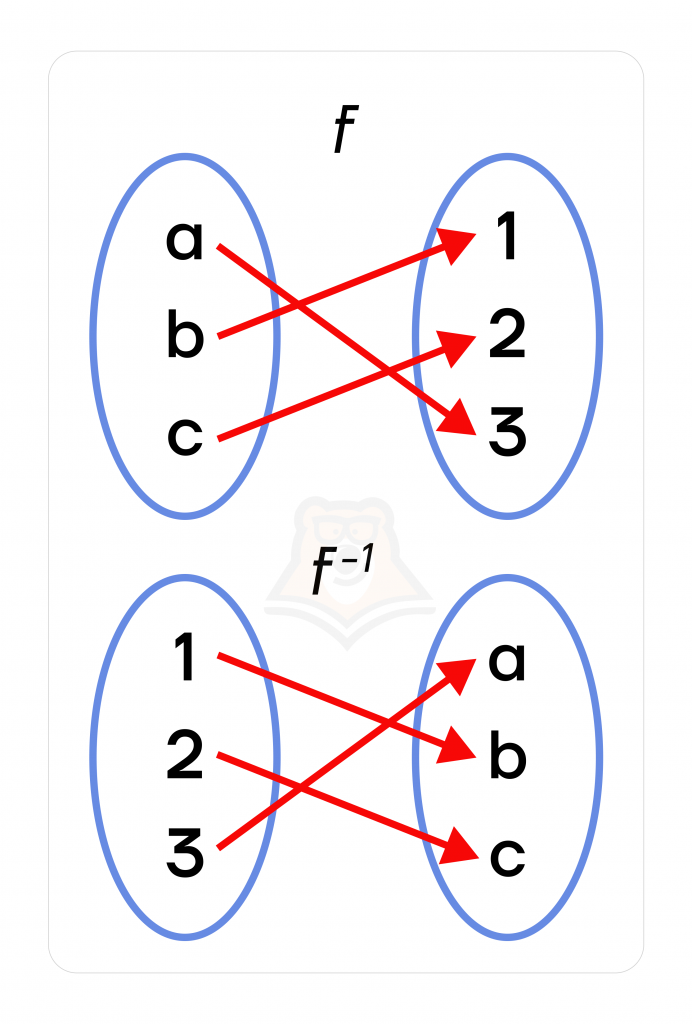
Например, \(y = 3x+2\).

Найдем обратную функцию:

\(3x=y-2\)
\(x=\frac{y-2}{3}=\frac{y}{3}-\frac{2}{3}\).

При этом не все функции имеют обратные функции, например, функция \(y=x^2\) обратной не имеет, так как нет однозначного соответствия между y и x, то есть одной y не соответствует один x.

Алгоритм получения обратной функции 

1 шаг: Выразить в исходной функции \(x\) через \(y\).

2 шаг: Для удобства поменять переменные, то есть вместо \(x\) записать \(y\), и наоборот.

Разберем пример: \(y=e^{2x}\)

Найдем зависимость \(x\) от \(y\):
\(2x=ln(y)\)
\(x=\frac{ln(y)}{2}\)

Поменяем переменные: 

\(y =\frac{ ln(x)}{2}\)- обратная функция к функции \(y = e^{2x}\).

Почему графики важны в мире инвестиций? Графиками пользуются почти все инвесторы, чтобы посмотреть, как ведут акции, облигации или другие финансовые инструменты. Опытные игроки на бирже по данным графиками и при использовании технического анализа, могут предугадать дальнейшую судьбу ценной бумаги. С помощью графиков можно отобразить многие важные характеристики инструмента: количество продаж, рыночная цена и даже технические индикаторы.

Свойства обратных функций: 

1. Если \(f^{-1}(x)\) обратная к \(f(x)\), тогда \(f(x)\) обратная к \(f^{-1}(x)\).

То есть вернемся к прошлому примеру: \(y=\frac{ln(y)}{2}\) — обратная функция к функции \(y = e^{2x}\), значит \(y = e^{2x}\) – обратная функция к функции \(y=\frac{ln(y)}{2}\).

2. Область определения исходной функции – область допустимых значений второй и наоборот.
   То есть допустимые значения x исходной функции – это допустимые значения y обратной и наоборот.

3. Исходная функция и функция, обратная к ней, симметричны относительно прямой \(y=x\).
   Построим функции \(y = 3x+2\) и
   \(y =\frac{ x}{3}-\frac{2}{3}\) (мы уже знаем, что они взаимно обратные) и убедимся, что симметричность действительно есть.

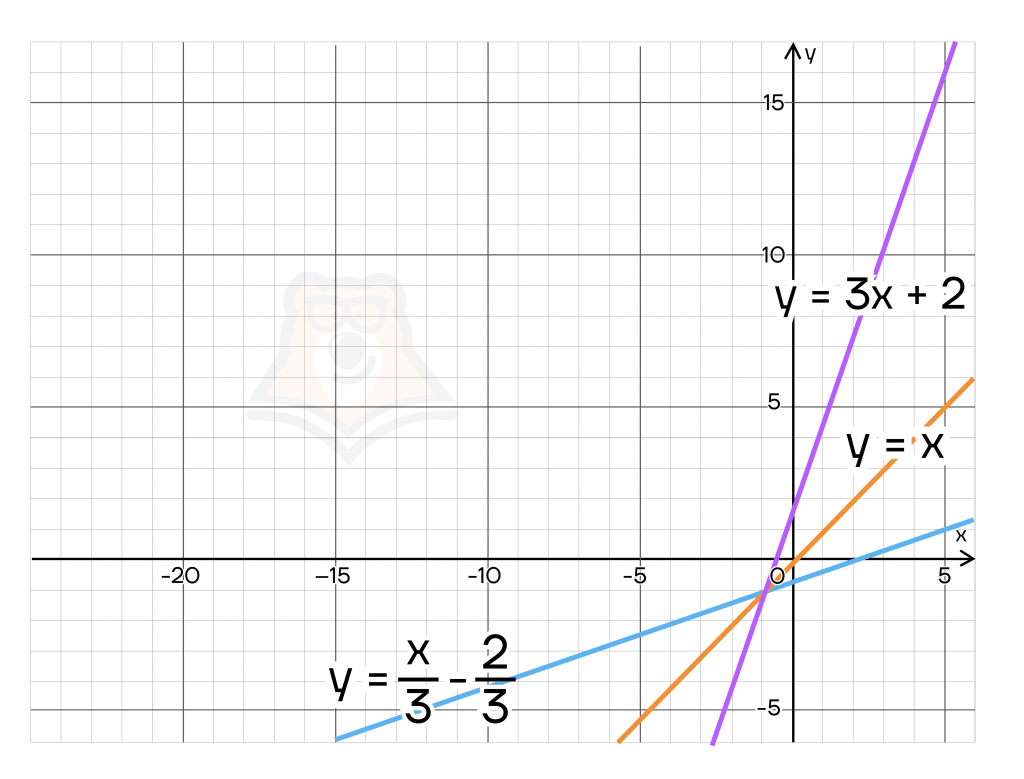
Преобразование графиков – очень важный навык для людей разных специальностей. Экономисты строят графики движения денег, физики – поведения мельчайших частиц, а математики – различных решений уравнений. Чтобы узнать, как этот навык может помочь вам на хорошо сдать ЕГЭ, читайте статью «Графический метод в задачах с параметром».

Термины

Аргумент функции – переменную, над которой совершается какое-либо математическое действие.

Асимптота – прямая, к которой неограниченно близко приближается график функции, но никогда ее не пересекает. 

Координатная плоскость – это плоскость, на которой можно определить положение точек с помощью числовых координат.

Область допустимых значений аргумента (область определения) – это все значения, которые может принимать аргумент функции.

Область допустимых значений функции – это все значения, которые может принимать функция.

Ось абсцисс – ось \(x\).

Ось ординат – ось \(y\).

Экспонента – функция вида \(y=e^x\), где \(е\) – число Эйлера, примерно равное 2,72. 

Фактчек

• Различные преобразования могут менять вид нашего графика: сжимать или растягивать его относительно различных осей координат.
• График, в котором присутствует модуль, при построении отражается относительно оси \(x\) или оси \(y\) в зависимости от положения модуля.
• Обратная функция – функция, которая обращает исходную зависимость. То есть была зависимость \(y\) от \(x\), а станет зависимость \(x\) от \(y\).
• Не у всех функций есть обратная функция, она есть только у тех функций, у которых один \(y\) соответствует одному \(x\).

Проверь себя

Задание 1.
Что происходит с функцией \(f(x)=2f(x)+1\)?

1. Сжимается в два раза вдоль оси \(y\) и переносится вверх на единицу.
2. Растягивается в два раза вдоль оси \(y\) и переносится вверх на единицу.
3. Сжимается в два раза вдоль оси \(х\) и переносится вверх на единицу.
4. Растягивается в два раза вдоль оси \(y\) и переносится вниз на единицу.

Задание 2.
В какую точку сдвинется начало координат для графика \(y=\frac{1}{x+3}+5\)?

1. (\(-3, 5\))
2. (\(3, 5\))
3. (\(-3, -5\))
4. (\(3, -5\))

Задание 3.
Какое преобразование происходит в случае, если функция заключена в модуль \((|f(x)|)\)?

1. Часть графика, лежащая в левой полуплоскости, отражается в правую полуплоскость относительно оси \(x\).
2. Часть графика, лежащая в правой полуплоскости, отражается в левую полуплоскость относительно оси \(x\).
3. Часть графика, лежащая в нижней полуплоскости, отражается в верхнюю полуплоскость относительно оси \(y\).
4. Часть графика, лежащая в верхней полуплоскости, отражается в нижнюю полуплоскость относительно оси \(y\).

Задание 4.
Какая функция не имеет обратной? 

1. \(y=x^3\)
2. \(y=\sqrt{x}\)
3. \(y=x-2\)
4. \(y=x^4\)

Задание 5.
Какая функция является обратной к функции \(y =2x+6\)?

1. \(y =\frac{x}{2}-3\)
2. \(y =\frac{x}{2}-6\)
3. \(y =x-3\)
4. \(y =x-6\)

Ответы: 1. — 2 2. — 1 3. — 3 4. — 4 5.— 1