Арифметическая прогрессия

На этой странице вы узнаете

• Как правильно расставить шары для бильярда в начале игры? 
• Как связана арифметическая прогрессия и литература?
• Как Карл Гаусс удивил своего учителя по математике?

Считаем ли мы овец перед сном, добавляем по монетке в копилку или достаем сухарик из упаковки — каждый раз мы сами того не осознавая применяем законы математики, которые рассмотрим в этой статье.

Понятие арифметической прогрессии 

Арифметическая прогрессия является видом числовых последовательностей. 

У арифметической прогрессии есть особенность: каждый следующий член отличается от предыдущего на одно и то же число. В последовательности 1, 2, 3, 4 и так далее — члены отличаются друг от друга на единицу. 

Арифметическая прогрессия – последовательность чисел, в которой каждый член начиная со второго, равен сумме предыдущего члена и разности прогрессии. 

Разность прогрессии – то число, на которое отличаются члены прогрессии друг от друга. Разность прогрессии обозначается буквой d. 

Арифметическую прогрессию можно задать формулой. 

\(a_{n+1}=a_n+d\)

Например, если мы хотим найти третий член арифметической прогрессии, то нужно воспользоваться формулой: \(a_3=a_2+d\)

Однако бывает, что известны только первый член прогрессии и ее разность. Как быть в этом случае?

Разберемся на примере. Допустим, мы читаем книгу. Количество прочитанных страниц может быть задано с помощью арифметической прогрессии, в которой разность прогрессии и первый ее член равны 1. 

Мы прочитали 10 страниц. Десятая страница будет десятым членом прогрессии. Это 1 + 1 + 1 + 1 +1 + 1 + 1 + 1 + 1 + 1 страниц, если считать их по отдельности. 

Выделим первую страницу отдельно: 1+(1+1+1+1+1+1+1+1+1)=1+9=1+1*9 

Теперь заменим десятый член прогрессии, первый член прогрессии и ее разность на буквенные обозначения: \(a_{10}=a_1+9*d\).

Заметим, что множитель перед d на один меньше, чем порядковый номер искомого члена прогрессии. Тогда получаем: \(a_{10}=a_1+(10-1)*d\)

Мы можем вывести формулу для n-го члена прогрессии. А выглядит она так. 

\(a_n=a_1+d(n-1)\)

Данная формула может встретиться на ОГЭ по математике в задании № 14.

Задание. При падении мяч в первую секунду прошел 3 метра, в каждую следующую на 5 метров больше. Найдите, сколько метров прошел мяч в 30 секунду?

Решение. Воспользуемся предыдущей формулой:

\(a_n=a_1+d(n-1)\)

В данной формуле по условию:
\(d = 5\)
\(a_1 = 3\)
\(n = 30\)

Тогда:
\(a_n=3+5(30-1)\)
\(a_n = 148\)

Ответ: 148

Как правильно расставить шары для бильярда в начале игры? Вспомним расстановку шаров в бильярде. Они ставятся в пять рядов, причем в первом ряду один шар, а в пятом — пять. Тогда, чтобы правильно разместить 15 шаров, нужно воспользоваться арифметической прогрессией. В каждом следующем ряду будет на один шар больше, следовательно, во втором ряду имеем 1 + 1 = 2 шара, в третьем ряду 2 + 1 = 3 шара, а в четвертом 3 + 1 = 4. Расставленные таким образом шары образуют форму треугольника.

Допустим, мы хотим купить джинсы. В магазине представлены три ценовых категории, которые отличаются друг от друга на одинаковую сумму. Мы знаем, что самые дешевые джинсы стоят 1000 рублей, а самые дорогие 3000 рублей. Как найти, сколько стоят джинсы во второй ценовой категории?

Попробуем найти разность арифметической прогрессии. 

Джинсы во второй категории будут стоить \(1000+d\), а чтобы найти стоимость третьей категории, нужно прибавить разность прогрессии ко второй категории. Получаем \(1000+d+d=1000+2d\).

Мы знаем, что самые дорогие джинсы стоят 3000 рублей. Получаем уравнение \(1000+2d=3000\), откуда можем выразить разность прогрессии:

\(d=\frac{3000-1000}{2}=1000\)

Тогда джинсы во второй ценовой категории будут стоить \(1000+1000=2000\) рублей. 

Можно ли как-то найти это значение, не прибегая к таким большим рассуждениям? Для этого достаточно найти среднее арифметическое двух соседних членов. 

\(a_n=\frac{a_{n-1}+a_{n+1}}{2}\)

Докажем это. Если рассмотреть член \(а_n\), то член до него будет равен \(a_{n-1}=a_n-d\), а член после него \(a_{n+1}=a_n+d\). Тогда их среднее арифметическое равно \(\frac{a_{n-1}+a_{n+1}}{2}=\frac{a_n-d+a_n+d}{2}=\frac{2a_n}{2}=a_n\). 

Проверим на нашей задаче. 

\(a_2=\frac{a_1+a_3}{2}=\frac{1000+3000}{2}=\frac{4000}{2}=2000\). Все верно. 

Чтобы найти разность прогрессии, достаточно вычесть из любого члена прогрессии предыдущий к нему. 

\(d=a_{n+1}-a_n\)

Как связана арифметическая прогрессия и литература? Вспомним строки из «Евгения Онегина»: …Не мог он ямба от хорея, Как мы не бились отличить… Ямб – это стихотворный размер, ударения в котором падают на четные слоги 2, 4, 6, 8, …, то есть получили арифметическую прогрессию. Другой стихотворный размер хорей, в нем ударения падают на нечетные слоги 1, 3, 5, 7, …,  что также является арифметической прогрессией.

Мы научились находить любой член арифметической прогрессии, а теперь узнаем, как найти сумму n-ого количества ее элементов. 

Разумеется, их можно сложить: \(a_1+a_2+a_3+…+a_n\). Но тогда нужно вычислять все члены прогрессии, а их может быть очень много. 

В этом случае используется формула суммы арифметической прогрессии. Ее удобство в том, что используются только первый и последний член прогрессии. 

\(S_n=\frac{a_1+a_n}{2}*n\)

Немного преобразуем формулу: 

\(S_n=\frac{a_1+a_n}{2}*n=\frac{a_1+a_1+d(n-1)}{2}*n=\frac{2a_1+d(n-1)}{2}*n\) — это формула суммы членов арифметической прогрессии через первый член и ее разность. 

Выделим полученную формулу:

\(S_n=\frac{2a_1+d(n-1)}{2}*n\)

Решим небольшую задачу. Марина решила сделать картину из страз. По схеме у нее есть 15 рядов, в каждом из которых страз на три больше, чем в предыдущем. В первом ряду 6 страз. Сколько всего страз понадобится, чтобы выложить эти ряды?

Воспользуемся формулой арифметической прогрессии. Но прежде найдем, сколько страз в последнем, пятнадцатом ряду:
\(a_{15}=6+3*(15+1)=6+3*14=6+42=48\)

Тогда по формуле суммы арифметической прогрессии всего Марине понадобится:
\(S_{15}=\frac{6+48}{2}*15=\frac{54}{2}*15=27*15=405\) страз. 

Формула суммы арифметической прогрессии используется в задачах из ЕГЭ по профильной математике. Например, в задании № 9.

Задание. Олесе надо решить 640 задач. Ежедневно она решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Олеся решила 10 задач. Сколько задач Олеся решила в последний день, если вся работа была сделана за 16 дней?

Решение. Вспомним формулу суммы арифметической прогрессии:

\(S_n=\frac{a_1+a_n}{2}*n\)

В данной формуле по условию:
\(S_n = 640\)
\(a_1 = 10\)
\(n = 16\)

Тогда:
\(640 =\frac{10 + a_n}{2}*16\)
\(640 = 8(10+a_n) | :8\)
\(80 = 10+a_n\)
\(a_n = 70\)

Ответ: 70

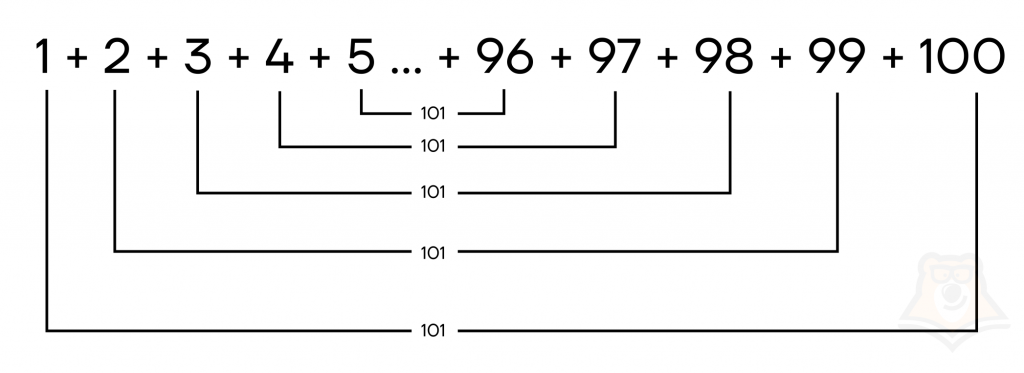
Как Карл Гаусс удивил своего учителя по математике? Карл Гаусс — немецкий математик, живший в 18–19 веках. На одном из уроков математики учитель задал сложить все цифры от 1 до 100. Карл Гаусс заметил, что суммы чисел, расположенных симметрично с противоположных сторон, одинаковые: \(1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101\) и так далее. Всего таких сумм получилось 50. Следовательно, быстро вычислить сумму этих цифр можно было как произведение \(101 * 50\). Такой способ работает для любой арифметической прогрессии. Внимательно посмотрим на сумму арифметической прогрессии. Пусть \(a_1=1, a_{100}=100, n=100\). Тогда получаем: \(S_{100}=\frac{1+100}{2}*100=101*50\), то есть Карл Гаусс использовал сумму арифметической прогрессии, сам того не зная.

Арифметическая прогрессия делится на несколько видов, разберем их.

Виды арифметических прогрессий

Существует всего три вида арифметической прогрессии. 

1. Возрастающая арифметическая прогрессия.
Разность прогрессии — положительное число, то есть d > 0, а каждый следующий член прогрессии больше предыдущего. 

Прогрессия 2, 4, 6, 8 является возрастающей. 

2. Убывающая арифметическая прогрессия.
Разность прогрессии — отрицательное число, то есть d < 0, а каждый следующий член прогрессии меньше предыдущего. 

Примером убывающей арифметической прогрессии может служить 100, 95, 90, 85 и так далее.  

3. Стационарная арифметическая прогрессия.
В этой арифметической прогрессии разность будет равна 0, то есть d = 0. Следовательно, члены прогрессии не будут отличаться друг от друга. 

Например, прогрессия 3, 3, 3, 3, 3 будет являться стационарной. 

Мы познакомились с одним из типов числовой последовательности, но на экзамене может встретиться другой: геометрическая прогрессия. Чем эта прогрессия отличается от арифметической, вы можете узнать в статье «Геометрическая прогрессия».

Фактчек

• Арифметическая прогрессия — последовательность чисел, в которой каждый следующий член равен сумме предыдущего члена и фиксированного числа (разности арифметической прогрессии).
• Разность арифметической прогрессии — это число, на которое предыдущий член арифметической прогрессии меньше или больше следующего.
• Чтобы найти n-ый член прогрессии, необходимо воспользоваться одной из трех формул: \(a_{n+1}=a_n+d, a_n=a_1+d(n-1)\) или \(a_n=\frac{a_{n-1}+a_{n+1}}{2}\). 
• Чтобы найти разность прогрессии, достаточно из любого члена прогрессии вычесть предыдущий ему член прогрессии. 
• По формуле \(S_n=\frac{a_1+a_n}{2}*n\) можно найти сумму n членов прогрессии. 
• Арифметическая прогрессия может быть убывающей, возрастающей или стационарной. 

Проверь себя

Задание 1.
Какая прогрессия является арифметической?

1. 3, 7, 11, 15
2. 1, 1, 2, 3, 5
3. 2, 4, 8, 16
4. 1, 4, 16, 25

Задание 2.
Первый член арифметической прогрессии равен 10, а ее разность равна –5. Найдите семнадцатый член арифметической прогрессии. 

1. Семнадцатого члена такой арифметической прогрессии не существует.
2. 0
3. −70
4. −75 

Задание 3.
Пятый член арифметической прогрессии равен 16, а седьмой член равен 20. Найдите шестой член арифметической прогрессии. 

1. 2
2. 18
3. 17,5
4. Невозможно найти шестой член арифметической прогрессии. 

Задание 4.
Каждый день Миша катается на велосипеде, причем с каждым разом увеличивает расстояние на 2 км. В первый день он проехал 3 км. Сколько всего км проедет Миша за пять дней?

1. 14
2. 17
3. 11
4. 35

Ответы: 1. — 1; 2. — 3; 3. — 2; 4. — 4.