Биномиальное распределение

На этой странице вы узнаете

• Что значит слово «бином»?
• Какой лайфхак придумал Ньютон?
• Как связаны бином Ньютона и биноминальное распределение?

Бином Ньютона, биноминальное распределение. Эти два термина звучат очень похоже. Но являются ли они одним и тем же, или же они применяются в разных заданиях ЕГЭ по профильной математике? Давайте разберемся с этими непонятными словами и с тем, как они могут нам помочь!

Бином Ньютона

Наверняка вы помните формулы квадрата суммы и, может быть, даже помните формулу куба суммы:

\((a+b)^2 = a^2+2ab+b^2\)
\((a+b)^3 = a^3+3a^2b+3ab^2+b^3\)

Если вы помните эти формулы, то вы уже знаете частные случаи бинома Ньютона. Если подзабыли эти формулы, то перечитайте статью про формулы сокращенного умножения. Так, а что это вообще такое этот бином Ньютона?

Ньютона все знают, это был такой английский физик, математик и астроном. 

Что значит слово «бином»? Бином состоит из двух латинских слов: bis  — дважды, и nomen — имя. Если говорить нормальным русским языком, то бином — это двучлен.

Да, те самые \((a+b)\) и \((c+3d)\), которые так часто встречались в школьных задачках, — биномы.

Какой лайфхак придумал Ньютон? Бином Ньютона позволяет раскрывать эти двучлены, если они возведены в любую натуральную степень: \((a+b)^2, (a+b)^3\) и даже \((a+b)^{100}\).

Формула бинома Ньютона, которая позволяет раскрывать это, выглядит так:

\((a+b)^n =C_n^0*a^n*b^0 + C_n^1*a^{n-1}*b^1+C_n^2*a^{n-2}*b^2 +…+C_n^{n-1}*a*b^{n-1}+C_n^n*a^0*b^n\)

Или в сокращенном варианте:

\((a+b)^n =\displaystyle\sum_{k=0}^n C_n^k*a^{n-k}*b^k\)

Так много непонятных символов, давайте разбираться.

• Буквы a и b означают два числа, которые мы хотим сложить и возвести в степень n.
• Причудливая буква \(\sum\) — сигма, которая означает алгебраическую сумму.
• \(C_n^k\) — биноминальный коэффициент, по совместительству число сочетаний. Считается он по следующей формуле:

\(C_n^k =\frac{n!}{k!*(n-k)!}\)

Знак «!» означает факториал — произведение всех чисел от 1 до самого числа. Например, \(5! = 1*2*3*4*5 = 120\). Формулу числа сочетаний и факториал мы подробно разбирали в статье «Основы комбинаторики».

Но есть более простой способ посчитать биноминальные коэффициенты. В этом нам поможет треугольник Паскаля. Запоминайте алгоритм. 

Сначала пишем цифру 1:

Затем добавляем еще две единички под ней:

Теперь по бокам будем писать единички, а между двумя предыдущими числами их сумму:

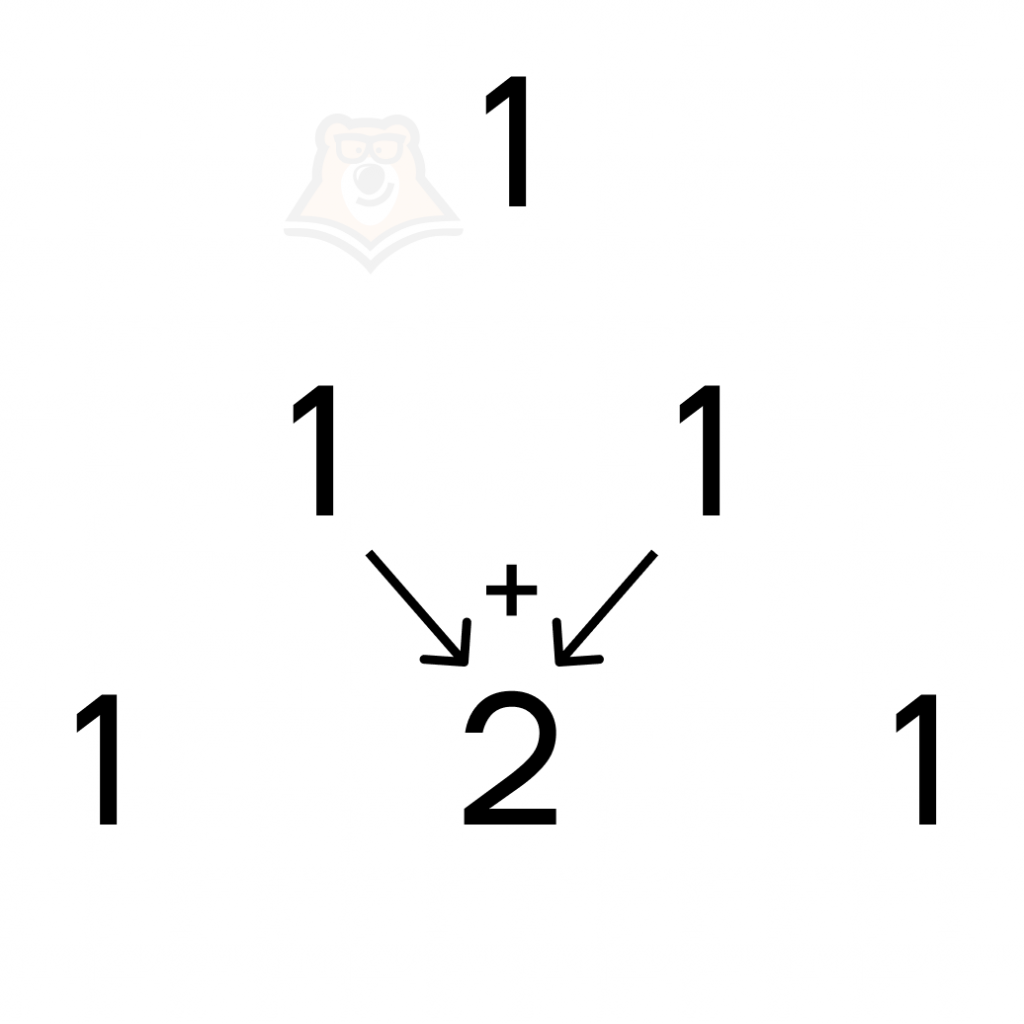
Сделаем так еще три раза:

У нас получился треугольник Паскаля, на каждом уровне которого — биноминальные коэффициенты. Легко, правда? Теперь давайте посмотрим, как это работает, на примере.

Пример 1. Расписать \((a+b)^2\) с помощью бинома Ньютона.

Решение. Распишем бином Ньютона для этого двучлена:

\((a+b)^2 =C_2^0*a^2*b^0 + C_2^1*a^1*b^1+C_2^2*a^0*b^2\)

Число в нулевой степени равно единице, сразу упростим:

\((a+b)^2 =C_2^0*a^2 + C_2^1*a^1*b^1+C_2^2*b^2\)

Подставим биноминальные коэффициенты с помощью треугольника Паскаля:

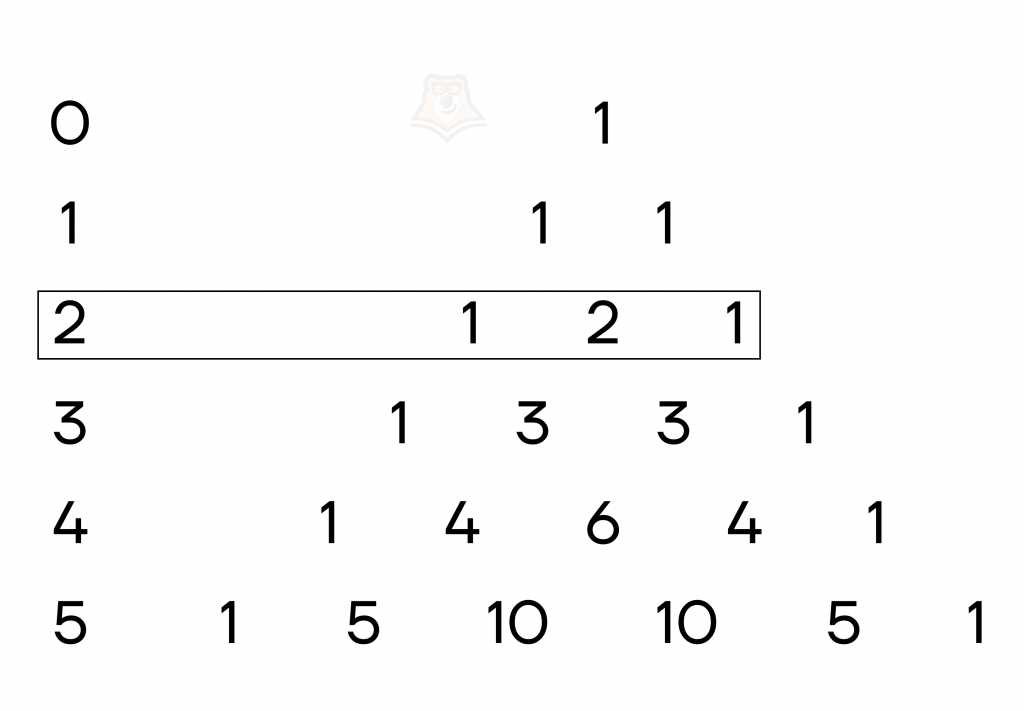
\((a+b)^2 =1*a^2 + 2*a*b+1*b^2\)

Получилась хорошо знакомая нам формула квадрата суммы.

Ответ: \((a+b)^2 =a^2 + 2ab+b^2\).

Теперь решим что-нибудь посложнее.

Решим пример, который может попасться на ЕГЭ по профильной математике в задании №13.

Задание. Решите уравнение \((x+1)^4 + (x-1)^4 = 16x^2\).

Решение. Возведем двучлены в четвертую степень, используя бином Ньютона и треугольник Паскаля:

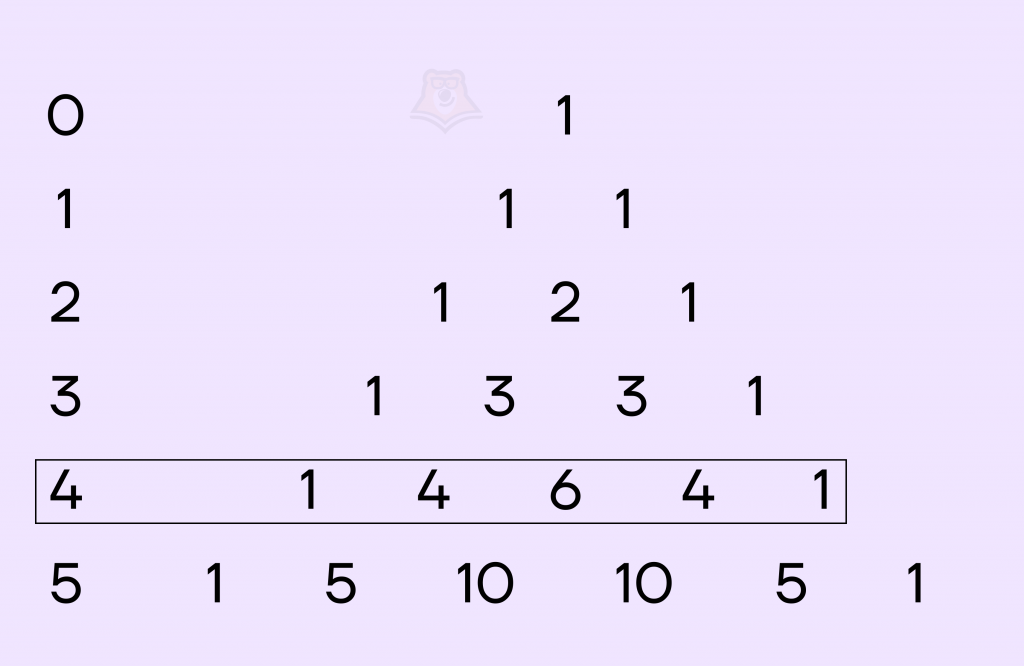
Получим:

\(x^4 + 4x^3+6x^2 +4x+1 +x^4*(-1)^0 + 4x^3*(-1)^1+6x^2*(-1)^2 +4x+(-1)^4  = 16x^2\)

Упростим:

\(2x^4 + 12x^2+2  = 16x^2\)

Переносим все в левую часть и упрощаем:

\(2x^4 -4x^2+2  = 0\)

Поделим обе части уравнения на \(2\):

\(x^4 -2x^2+1  = 0\)

Решим получившееся уравнение, воспользовавшись формулой сокращенного умножения — квадратом разности:

\((x^2-1)^2=0\)
\(x^2-1=0\)
\(x^2=1\)

Избавимся от второй степени с помощью квадратного корня и получим:

\(x = 1\)
\(x = -1\)

Ответ: \(x= ±1\)

Страшное на первый взгляд уравнение свернулось в обычное квадратное. В этом и есть вся прелесть бинома Ньютона. Теперь узнаем, что такое биноминальное распределение. 

Биноминальное распределение

Сначала познакомимся с формулой Бернулли. Выглядит она следующим образом:

\(P_n^k=C_n^k*p^k*q^{n-k}\)

Да, формула чем-то похожа на формулу бинома Ньютона, но применяется она для нахождения вероятностей. Эта формула помогает находить вероятность того, что событие наступит ровно k раз в n независимых испытаниях, если вероятность наступления события во всех испытаниях постоянна. Но важно отметить, что работает формула Бернулли только тогда, когда у события есть всего два исхода: «удача» и «неудача». Формула сработает, например, в задачах с броском монетки, а в задачах про три шарика разных цветов — нет. Почитать про вычисление вероятностей можете в статье «Вычисление вероятностей».

Здесь \(C_n^k\) — количество сочетаний из n по k; k — число успехов; n — серия испытаний; p — вероятность наступления некоторого события; q — вероятность ненаступления этого события, \(q=1-p\). Опробуем эту формулу на примере, чтобы она стала понятнее.

Пример 2. При передаче сообщения вероятность искажения одного знака равна 0,2. Найти вероятность того, что сообщение из 10 знаков содержит 2 искажения.

Решение. Воспользуемся формулой Бернулли. Имеем:

\(n = 10, k = 2, p = 0,2, q=0,8\)
\(P_{10}^3=C_{10}^2*(0,2)^2*(0,8)^{10-2}\)

Распишем сочетание по формуле:

\(C_n^k =\frac{ n!}{k!*(n-k)!}\)
\(P_{10}^3=\frac{10!}{2!*8!}*(0,2)^2*(0,8)^8\)
\(P_{10}^3=\frac{1*2*3*4*5*6*7*8*9*10}{1*2*1*2*3*4*5*6*7*8}*(0,2)^2*(0,8)^8\)
\(P_{10}^3=9*102*(0,2)2*(0,8)8\)
\(P_{10}^3=45*0,04*0,168\)
\(P_{10}^3=45*0,04*0,168\)
\(P_{10}^3 ≈ 0,3024\)

Ответ. \(0,3024\)

Так, а причем здесь биноминальное распределение?

На самом деле, биноминальным называют такое распределение, которое определяется формулой Бернулли.  

Проще всего будет сразу же разобрать на примере.

Пример 3. В городе есть 3 коммерческих банка. У каждого из них есть риск банкротства, который равен 10%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.

Решение. Пусть Х — величина, равная количеству банков, которые могут обанкротиться в следующем году. Возможны случаи, когда обанкротились 0, 1, 2, или 3, поэтому это все значения, которые может принимать Х. Воспользуемся формулой Бернулли, чтобы посчитать все вероятности:

\(P(X=0) =C_3^0*(0,1)^0*(0,9)^3 = 0,729\)
\(P(X=1) =C_3^1*(0,1)^1*(0,9)^2 = 0,243\)
\(P(X=2) =C_3^2*(0,1)^2*(0,9)^1 = 0,027\)
\(P(X=3) =C_3^3*(0,1)^3*(0,9)^0 = 0,001\)

Теперь составим таблицу биноминального распределения величины Х:

Значения X	0	1	2	3
Вероятности	0,729	0,243	0,027	0,001

Все расчеты верные, так как сумма всех вероятностей равна 1.

Как связаны бином Ньютона и биноминальное распределение? Получается, что бином Ньютона и биноминальное распределение, хоть и называются похоже и формулы имеют почти одинаковые, на самом деле штуки разные и применяются в разных заданиях ЕГЭ по профильной математике.

У биноминального распределения есть некоторые свойства. Давайте рассмотрим их.

Свойства биноминального распределения

1. Возможно всего два исхода: успех или неудача. Например, при броске монетки может выпасть либо орел, либо решка.
2. Испытания независимы. Предыдущий бросок монетки никак не повлияет на исход очередного броска.
3. Биномиальное распределение применяется, когда проводится фиксированное количество независимых испытаний. Например, если мы договорились, что бросков монетки будет 50, тогда мы сможем использовать биноминальное распределение.
4. Сумма вероятностей равна 1. При броске монеты мы имеем вероятность выпадения решки равной 0,5. Вероятность выпадения орла такая же. В сумме получается 1. Это значит, что какое-то событие точно произойдет.
5. Вероятности успеха и неудачи фиксированы. При броске монетки вероятности выпадения орла и решки всегда равны 0,5. 

Биноминальное распределение может понадобиться для нахождения математического ожидания — суммы произведений значения на вероятность. Еще может встретиться дисперсия — величина, которая измеряет, насколько далеко набор чисел разбросан от их среднего значения. Формула у дисперсии такая:

\(D(X) = np(1-p)\)

Здесь \(n\) — число испытаний; \(p\) — вероятность успеха; \(q\) — вероятность неудачи, равна \((1-p)\).

Решим пример, который может попасться на ЕГЭ по профильной математике в задании №5.

Задание. В таблице показано распределение случайной величины Х. Найдите EX — математическое ожидание этой случайной величины.

Решение. Мы знаем, что математическое ожидание для биноминального распределения — сумма произведений значения на вероятность. Получаем:

\(EX = 0*0,4+2*0,2 +6*0,1+8*0,3 = 0,4+0,6+2,4=3,4\)

Ответ: \(3,4\)

Итак, в этой статье мы разобрали, что такое бином Ньютона, биноминальное распределение и какие свойства у последнего. В следующей статье мы узнаем, как решать линейные и квадратные уравнения и неравенства с параметрами.

Термины

Дисперсия — величина, которая измеряет, насколько далеко набор чисел разбросан от их среднего значения.

Математическое ожидание для биноминального распределения — сумма произведений значения на вероятность.

Фактчек

• Бином Ньютона — способ разложения двучленов, которые возведены в любую натуральную степень.
• Биноминальные коэффициенты необязательно считать по формуле с факториалами. Можно использовать треугольник Паскаля.
• Биноминальное распределение — такое распределение, которое определяется формулой Бернулли.
• Свойствами биноминального распределения являются: два исхода, независимость испытаний, фиксированность количества испытаний и вероятностей успеха и неудачи и сумма вероятностей.
• Хоть бином Ньютона и биноминальное распределение называются похоже, они применяются в разных заданиях ЕГЭ по профильной математике.

Проверь себя

Задание 1.
Где написана правильная формула бинома Ньютона?

1. \((a+b)^n =\displaystyle\sum_{k=0}^n C_n^k*a^{n-k}*b^k\)
2. \((a+b)^n = C_n^k*a^{n-k}*b^k\)
3. \((a+b)^n = \displaystyle\sum_{k=0}^n C_n^k*a^{n-k}\)
4. \((a+b)^n =\displaystyle\sum_{k=0}^n C_n^k*b^k\)

Задание 2.
Каковы биноминальные коэффициенты для бинома пятой степени?

1. \(1, 2, 3, 4, 5\)
2. \(1, 5, 10, 5, 1\)
3. \(1, 5, 10, 10, 5, 1\)
4. \(1, 5, 10, 15, 20, 25\)

Задание 3.
Что такое математическое ожидание для биноминального распределения?

1. Сумма произведений количества испытаний на вероятность успеха и на неудачи
2. Сумма произведений значения на вероятность
3. Сумма всех значений
4. Сумма всех вероятностей

Задание 4.
Какое из приведенных утверждений является верным свойством биноминального распределения?

1. Сумма вероятностей равна \(100\)
2. Количество испытаний должно быть нефиксированное
3. Может быть любое количество исходов
4. Вероятности успеха и неудачи фиксированы

Ответы: 1. — 1; 2. — 3; 3. — 2; 4. — 4.