Основные элементарные функции. Часть 2

На этой странице вы узнаете

• Как поменять любую функцию?
• Где можно встретить параболу в реальной жизни?
• Как связаны дискриминант, количество решений и парабола? 

Как можно быстро увидеть все значения функции? Ответ: построить ее график. Более того, график настолько незаменимая вещь, что по нему можно сразу понять все основные свойства функции!

Существуют несколько видов функции, которые имеют похожие свойства и графики. Некоторые из них – постоянную, линейную функции и гиперболу мы уже разобрали в статье «Основные элементарные функции. Часть 1». Там же мы узнали про прямоугольную систему координат, в которой и строятся графики функций. 

Сейчас мы рассмотрим еще несколько основных функций. 

Функция корня n-ой степени

В предыдущей статье мы уже совершали с переменной несколько операций: складывали, вычитали, умножали, делили. Теперь рассмотрим еще одну: извлечение корня. 

Поскольку переменную можно внести под знак корня, мы получаем функцию следующего вида: 

\(y=\sqrt[n]{x}\), где
\(n\) – натуральное число.

Для работы с данной функцией нам понадобятся свойства корней. Подробнее про корни вы можете прочитать в статье «Понятие корня». 

В зависимости от значения n корни имеют разные свойства. Основным критерием для разделения видов корней может быть четность (то есть делимость на 2) их степени. 

В зависимости от значения n функция может поменять свой вид и свойства, поэтому рассматривать мы будем каждый случай отдельно. 

Функция корня нечетной степени

В этом случае вместо n будет стоять любое нечетное число. Разберем такие функции на примере \(y=\sqrt[3]{x}\).

Первым делом стоит отметить, что под корнем может стоять любое число, поскольку ограничений для корней нечетной степени нет. Поэтому область определений будет любой х или \(D(y)=(-\infty;+\infty)\). 

Составим таблицу. 

х	-8	-1	0	1	8
у	-2	-1	0	1	2

Отметим на координатной плоскости полученные точки и соединим их плавной линией:

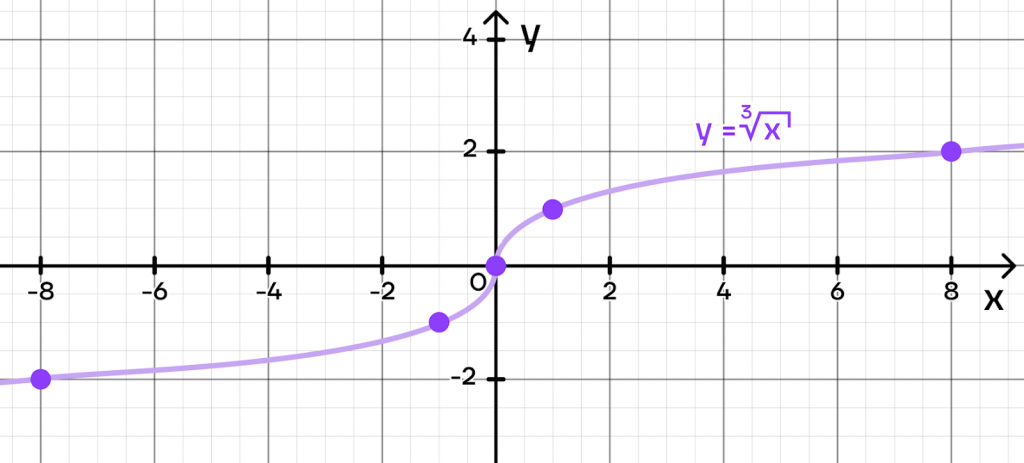
Запишем основные свойства такой функции.

Свойства функции корня нечетной степени:

1. Область определения \(D(y)=(-\infty;+\infty)\)
2. Область значений: \(E(y)=(-\infty;+\infty)\)
3. Возрастает на всей области определения.
4. Не существует ни наименьшего, ни наибольшего значения.
5. Непериодическая.

Поменяется ли что-то, если степень корня будет четной? Рассмотрим такие функции. 

Функция корня четной степени

В первую очередь у нас появляются ограничение: подкоренное число не может быть отрицательным. Следовательно, область определения будет равна \(D(y)=[0;+\infty)\). 

Разберем такие функции на примере функции квадратного корня. 

Функция квадратного корня – это функция вида \(y=\sqrt x\), где \(x\geq 0\) .

В жизни такая функция часто используется для определения стороны квадрата при известной площади. Например: при проектировании дома или разбиения участка земли на квадраты.

Построим таблицу для этой функции. 

x	0	1	4	9
y	0	1	2	3

Далее отметим точки на графике и соединим их плавной линией. 

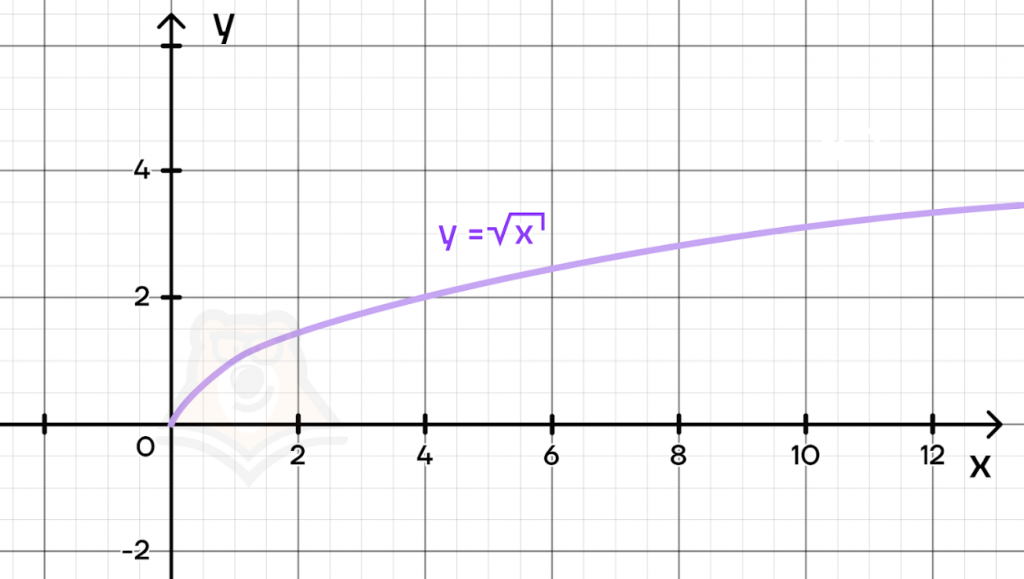
В этой функции у нас появляется наименьшее значение: у не может быть меньше 0, поскольку при извлечении корня четной степени не может получиться отрицательное число. Следовательно, график никогда не будет лежать ниже оси х. 

По графику мы также можем определить остальные свойства этой функции. 

Свойства функции квадратного корня:

1. Область определения: \(D(y)=[0;+\infty)\)
2. Область значений функции: \(E(y)=[0;+\infty)\)
3. Наименьшее значение при \(y = 0\).
4. Непериодическая.
5. Возрастает на всей области определения.

А теперь попробуем чуть-чуть поменять функции. В статье «Основные элементарные функции. Часть 1» мы уже рассматривали способы изменения функции. Также и тут: функцию можно сдвинуть вдоль оси у и вдоль оси х. 

Как поменять любую функцию?   Чтобы сдвинуть функцию вдоль оси у, достаточно прибавить или вычесть число к самой функции:  \(y=f(x)+n\) А вот, чтобы сдвинуть функцию вдоль оси х, необходимо прибавить или вычесть число из аргумента функции:  \(y=f(x+c)\)

Какие бывают сдвиги функции корня?

1. Сдвиг по оси у задается формулой \(y=\sqrt{x}+n\). При этом: 

Сдвиг вверх	Сдвиг вниз
n>0	n<0

Например, чтобы сдвинуть функцию на две единицы вниз, необходимо задать уравнение \(y=\sqrt{x}-2\). График такой функции будет выглядеть следующим образом:

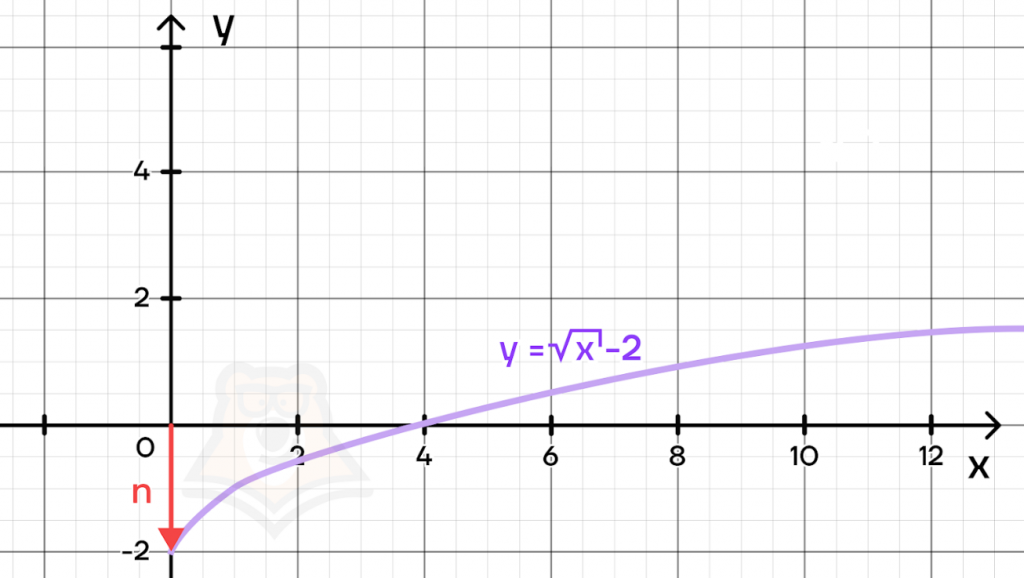
2. Сдвиг по оси х. В этом случае необходимо прибавить число к аргументу функции, то есть к х. Тогда функция приобретает вид \(y=\sqrt{x+c}\).
   
   Вспомним, что если мы прибавляем число, функция двигается в отрицательное направление. И наоборот, если мы вычитаем число, то функция двигается в положительном направлении. 

Сдвиг влево	Сдвиг вправо
c>0	c<0

Например, если мы хотим сдвинуть функцию на две единицы вправо, то необходимо записать уравнение \(y=\sqrt{x-2}\). График такой функции будет выглядеть следующим образом: 

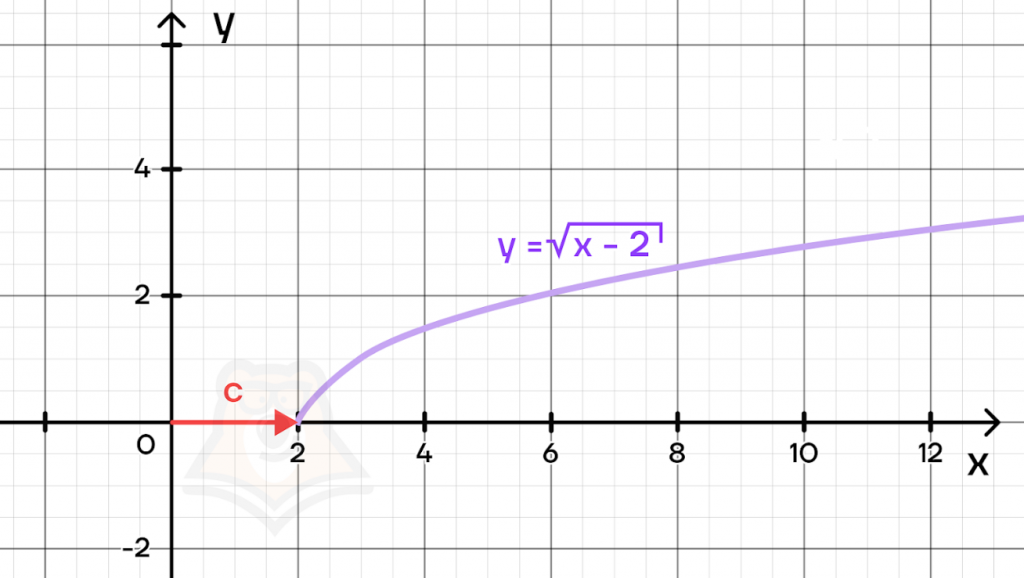
Функции с корнями могут встретиться на ЕГЭ по профильной математике в №10.
 
На рисунке изображен график функции \(f(x)=k\sqrt{x}\). Найдите f(2,89).

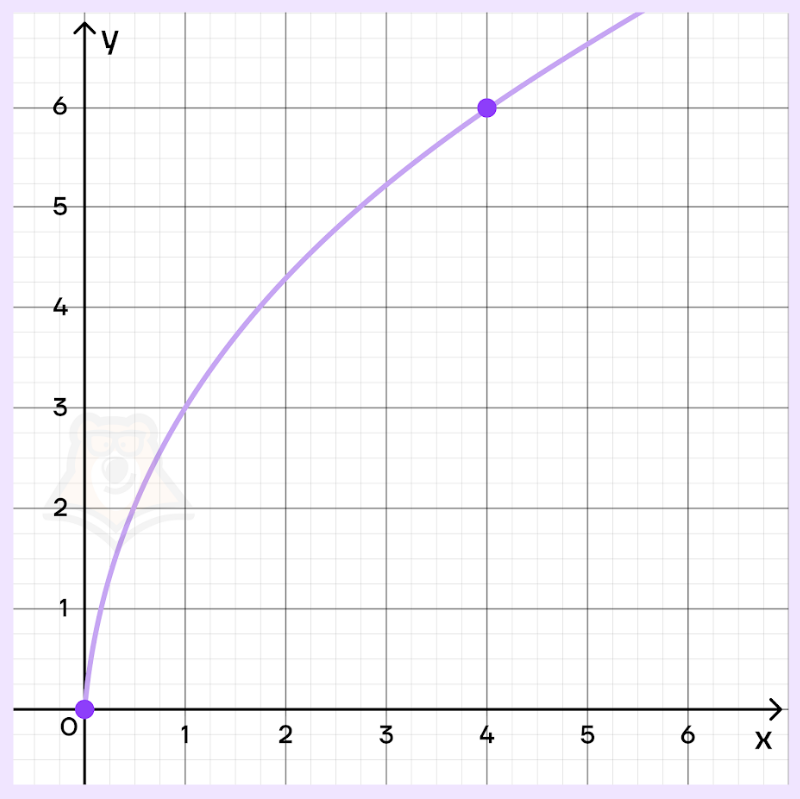
Решение.
По рисунку мы можем определить координату одной из точек: (4;6). Подставим ее в формулу:

\(y=k\sqrt x\)
\(6=k\sqrt 4\)
\(6=2k\)
\(k=3\)

Следовательно, получаем функцию \(f(x)=3\sqrt x\).

Теперь найдем \(f(2,89)\). Для этого подставим \(x=2,89\):

\(f(2,89)=3\sqrt{2,89}=3*1,7=5,1\)

Ответ: 5,1

Итак, мы разобрались, как выглядят функции, если переменная стоит под корнем. Какая обратная операция извлечению корня? Это возведение в степень. 

Степенная функция

Если мы возведем переменную в степень, то получим функцию вида:

\(y=x^a\)

Как и в случае с корнем, вместо а может стоять любое число. Начнем рассматривать функции с нечетным показателем степени. 

Для примера возьмем функцию \(y=x^3\) и составим для нее таблицу:

х	-2	-1	0	1	2
у	-8	-1	0	1	8

Отметим точки на координатной плоскости и построим график: 

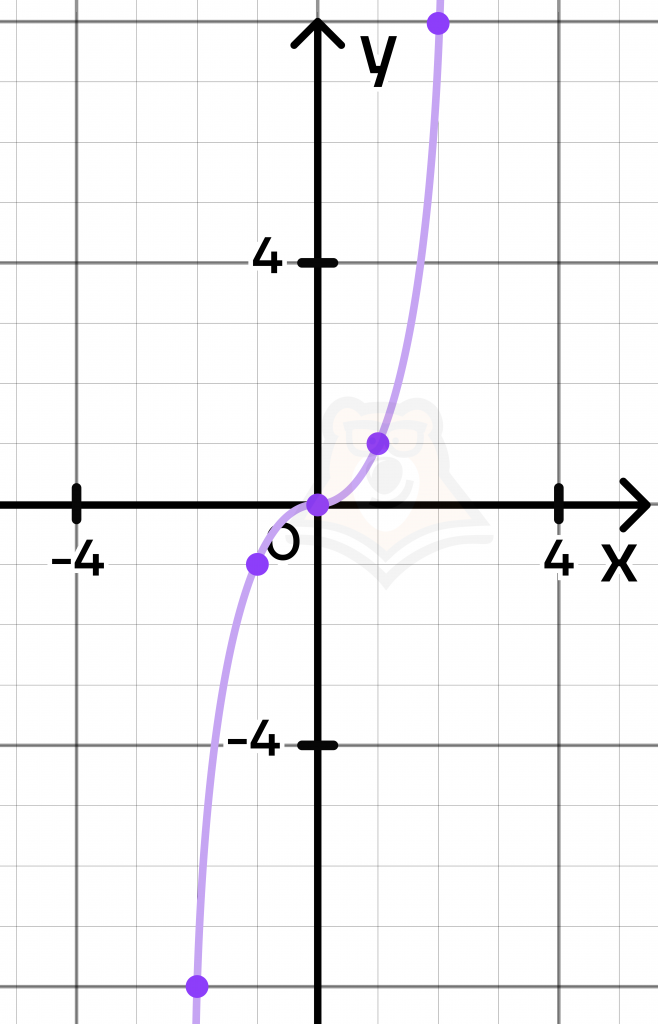
Если внимательно приглядеться, то можно заметить, что по форме график очень напоминает функцию \(y=\sqrt[3]{x}\). В этом нет ничего удивительного, поскольку эти функции – одно и то же действие, произведенное в «разные» стороны (поскольку извлечение корня – обратная операция возведению в степень). 

Рассмотрим свойства этой функции. 

Свойства степенной функции с нечетным положительным показателем степени:

1. Область определения \(D(y)=(-\infty;+\infty)\).
2. Область значений \(E(y)=(-\infty;+\infty)\).
3. Возрастающая.
4. Нет ни наименьшего, ни наибольшего значения.
5. Непериодическая.
6. Нечетная функция.

А теперь попробуем возвести переменную в нечетную отрицательную степень. Для примера рассмотрим функцию \(y=x^{-3}\). 

Преобразуем выражение по свойству степеней: \(a^{-n}=\frac{1}{a^n}\). Тогда мы получим функцию вида:

\(y=\frac{1}{x^3}\)

Перед нами снова появилась гипербола, о которой мы говорили в статье «Основные элементарные функции. Часть 1». График почти не будет отличаться, за исключением того, что х нужно будет возвести в куб. Составим таблицу:

х	-2	-1	1	2
у	\(-\frac{1}{8}\)	-1	1	\(\frac{1}{8}\)

Отметим точки и построим график функции. 

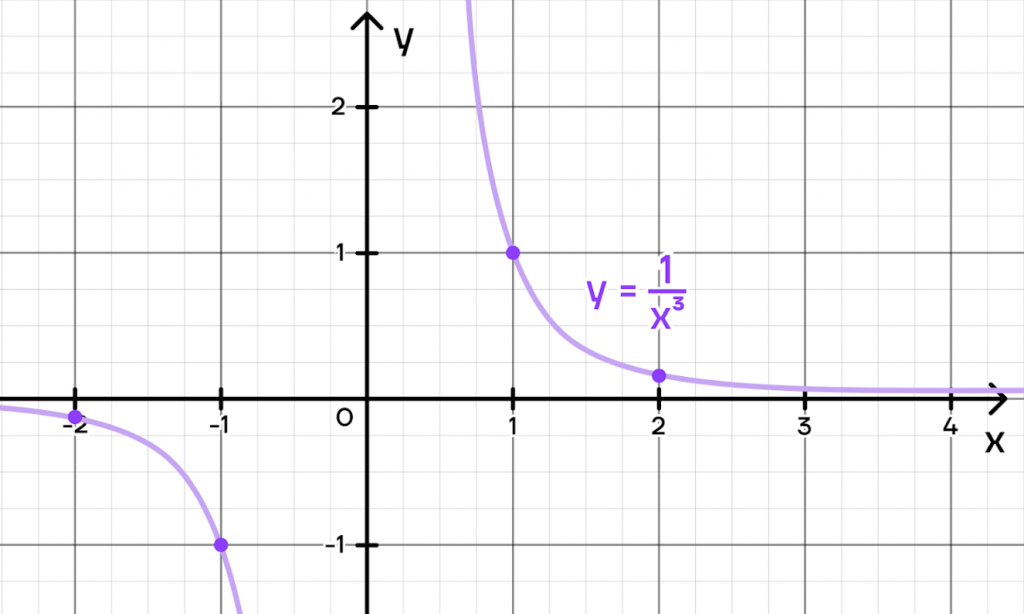
График такой функции будет обладать очень похожими с гиперболой свойствами. 

Свойства степенной функции с нечетным отрицательным показателем степени:

1. Область определения: \(D(y)=-\infty;00;+\infty\).
2. Область значений функции: \(E(y)=-\infty;00;+\infty\).
3. Наименьшего и наибольшего значений не существует.
4. Непериодическая.
5. Убывающая на промежутках \((-\infty;0)\) и \((0;+\infty)\).
6. Нулей нет.
7. Нечетная.

При возведении в отрицательную степень легко перейти к гиперболе. Но что получится, если при этом степень будет четной? Рассмотрим на примере функции \(y=x^{-2}\). 

По свойству степеней преобразуем ее в функцию вида \(y=\frac{1}{x^2}\).

В предыдущем примере у мог принимать отрицательные значения, поскольку при возведении отрицательного числа в нечетную степень получается отрицательное число. Но если мы попробуем возвести такое число в четную степень, то получим положительное число. Например, \((-2)^2=4\). 

Следовательно, для данной функции область значений будет \(y>0\), откуда получаем, что график функции будет лежать над осью х. 

Но что тогда делать с ветвью гиперболы в третьей четверти? Подробнее про нумерацию четвертей вы можете узнать в статье «Основные элементарные функции. Часть 1». 

Поскольку х может принимать отрицательные значения, то эта ветвь никуда не денется. Она просто будет «отзеркалена» вдоль оси х и теперь будет лежать во второй четверти. 

Составим таблицу для данной функции. 

х	-3	-2	-1	1	2	3
у	\(\frac{1}{8}\)	\(\frac{1}{4}\)	1	1	\(\frac{1}{4}\)	\(\frac{1}{8}\)

Отметим точки на графике и соединим их плавной линией: 

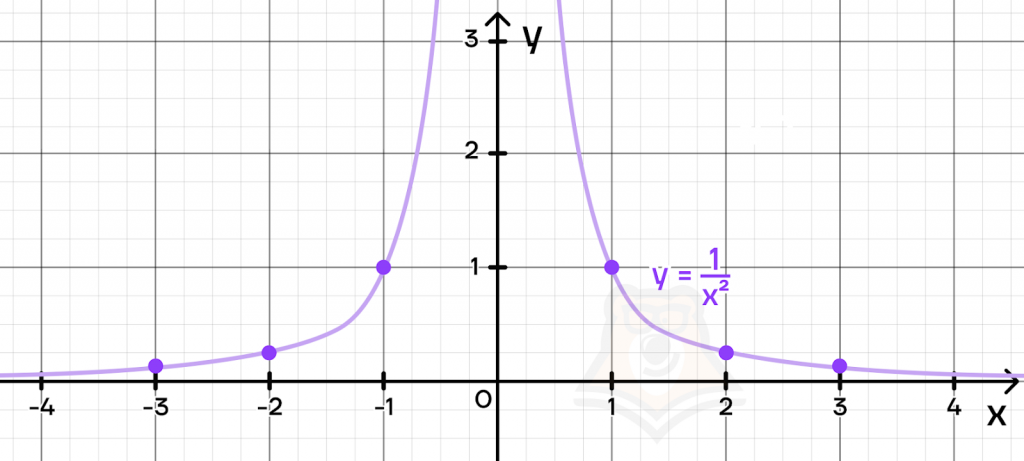
При этом асимптоты сохранятся такие же, как для гиперболы: \(x\neq 0, y\neq 0\).

Запишем свойства степенной функции с отрицательным четным показателем. 

1. Область определения: \(D(y)=-∞;00;+∞\)
2. Область значений функции: \(E(y)=0;+∞\)
3. Наименьшего и наибольшего значений не существует.
4. Непериодическая.
5. Возрастает на промежутке \((-\infty;0)\) и убывает на промежутке \((0;+\infty)\).
6. Нулей нет.
7. Четная.

Нам осталось рассмотреть еще один вид степенной функции – это функцию с четным положительным показателем степени. Примерами такой функции могут служить \(y=x^2, y=x^4, y=x^{10}\) и так далее. 

Разбирать мы будем на примере \(y=x^2\), поскольку это наиболее встречающаяся функция, которая требует к себе особого внимания. Называется она квадратичной функцией. 

Квадратичная функция

Квадратичная функция – это функция вида \(y=ax^2\), где a – известное число и \(a\neq 0\), графиком которой является парабола.

Но на самом деле мы можем еще расширить понятие квадратичной функции. Задаваться она будет квадратным уравнением:

\(y=ax^2+bx+c\), где \(a, b, c\) – известные числа; \(x\) – переменная.

Тогда функция \(y=ax^2\) будет частным случаем, когда \(b=c=0\). 

Эта функция не просто так задается квадратным уравнением. Она очень тесно связана с ним, поэтому перед дальнейшим ее изучением предлагаем вспомнить про квадратные уравнения.

При этом каждый из коэффициентов влияет на график функции. Разберемся, как именно. 

Влияние коэффициентов на график квадратичной функции

График квадратичной функции называется параболой. Построим обычную параболу без коэффициентов, которая задается формулой \(y=x^2\). Составим таблицу:

х	-2	-1	0	1	2
у	4	1	0	1	4

Отметим точки на плоскости и соединим их плавной линией. Как можно заметить по графику, парабола – симметричная кривая.

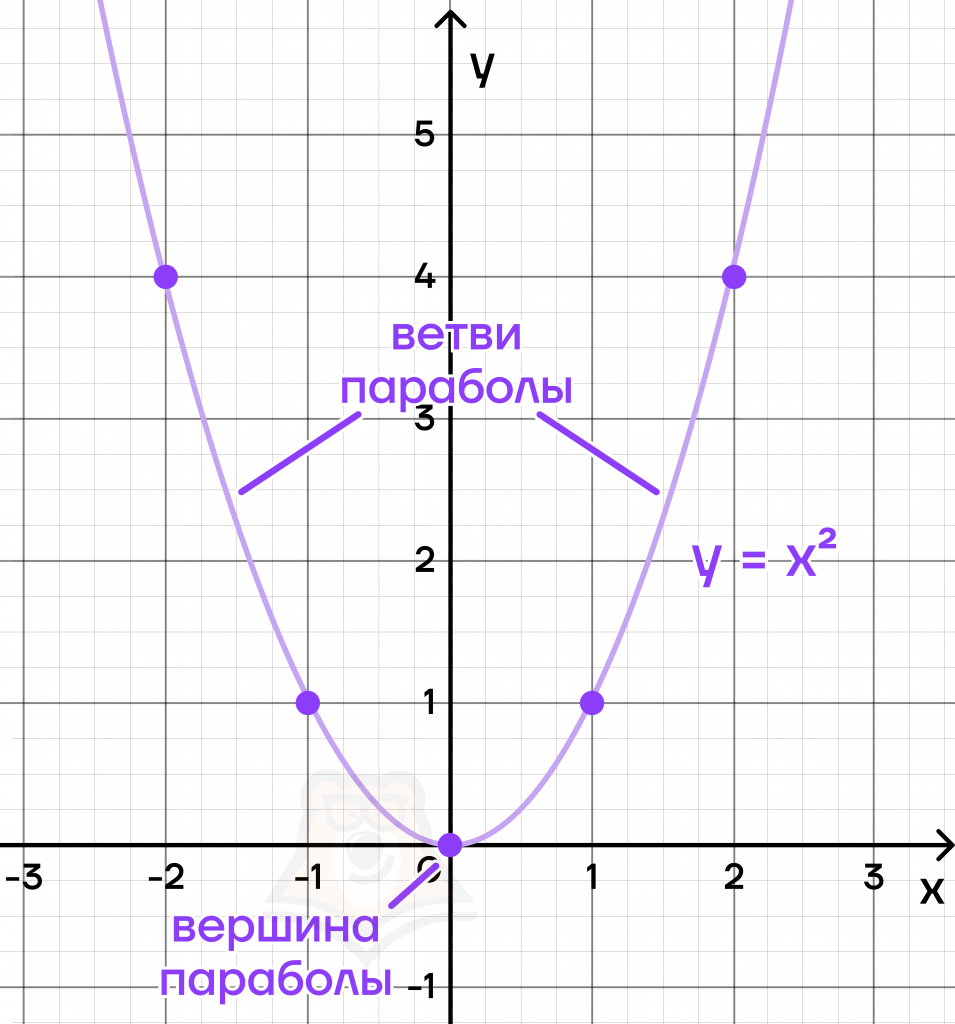
Самая «выступающая» точка называется вершиной параболы. В нашем случае это точка с координатами (0;0). Через нее также проходит ось симметрии параболы. 

А вот кривые, которые выходят из вершины, называются ветвями параболы.

Где можно встретить параболу в реальной жизни? Например, параболой можно описать полет мяча в баскетбольную корзину. Движение по параболе будет и у любого другого объекта, брошенного вверх.  Параболы применяются в архитектуре, в частности, для проектирования куполов.  Парабола нужна даже в космосе! Если некое тело запустить в космос со скоростью 7,9— 11,2 км/с, то оно станет спутником земли. Но если оно разовьет скорость большую, чем 11,2 км/с, то оно вновь начнет двигаться по параболе и улетит от Земли.

На форму параболы влияют все три коэффициента: а, b и с. 

1. Коэффициент а.

В зависимости от коэффициента а парабола может поменять направление ветвей или их расположение относительно друг друга. 

Мы уже рассмотрели выше случай, когда \(a=1\). Ветви такой параболы направлены вверх, а по рисунку она напоминает овраг. 

А вот если коэффициент а будет отрицательным, то ветви параболы будут направлены вниз, а график будет напоминать гору. 

Например, так будет выглядеть график параболы \(y=-x^2\). 

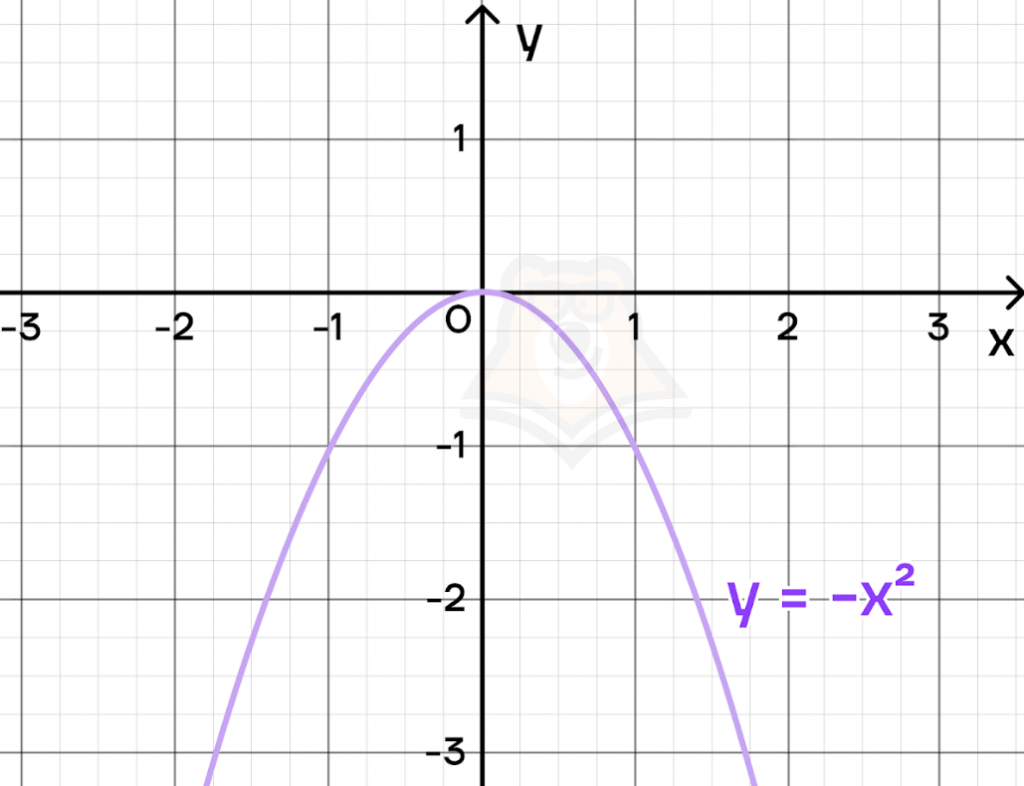
Однако этот коэффициент может менять свое значение. В этом случае парабола будет «сужаться» и расширяться. 

Если коэффициент а положителен, то:

• Чем больше коэффициент а, тем уже парабола.
• Чем меньше коэффициент а, тем шире парабола. 

Изобразим на графике три такие параболы. 

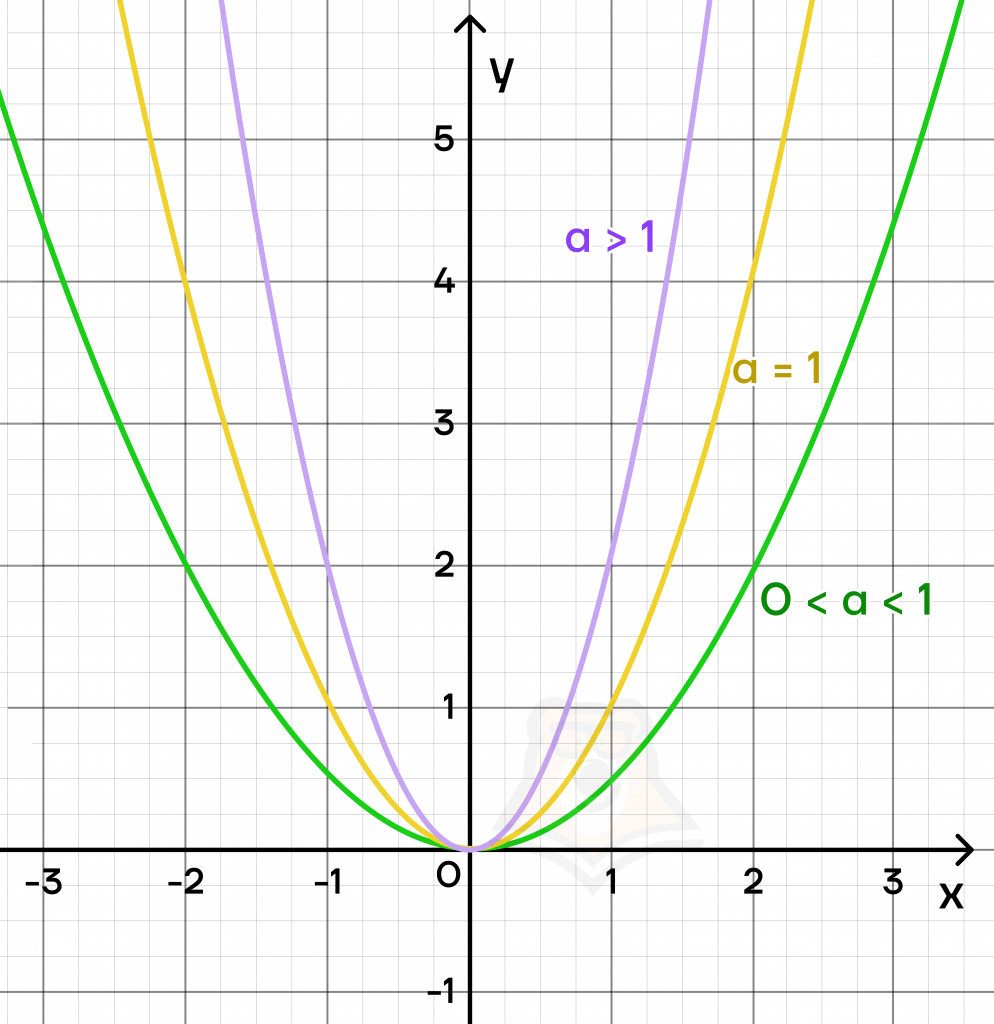
Стоит отметить, что в случае с отрицательным значением коэффициента а ситуация обратная:

• Чем больше значение коэффициента а, тем шире парабола.
• Чем меньше значение коэффициента а, тем уже парабола. 

Их графики будут выглядеть так: 

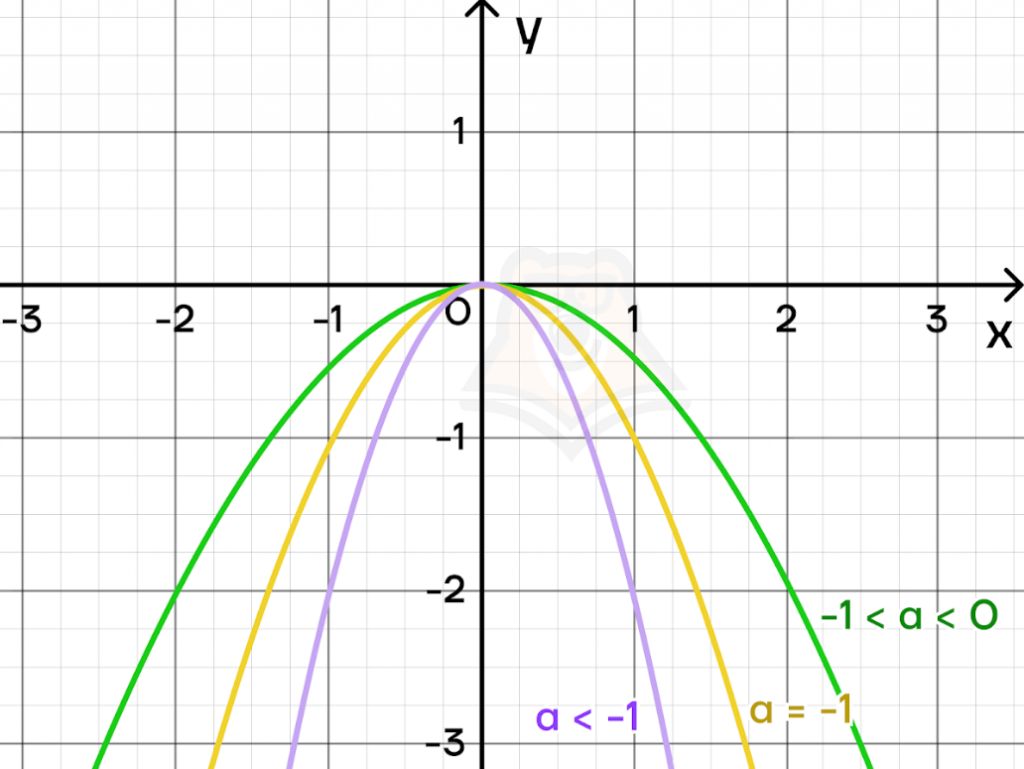
Все рассмотренные нами случаи влияют только на форму параболы и направление ее ветвей. Может ли она как-то смещаться по координатной плоскости?

2. Коэффициент b.

Смещение параболы проще всего отследить по ее вершине. И коэффициент b как раз отвечает за ее смещение вдоль оси х. 

• Если \(b>0\), то парабола смещается влево.
• Если \(b<0\), то парабола смещается вправо. 

На графиках это выглядит следующим образом: 

Коэффициент b напрямую связан с вершиной, находить которую мы научимся чуть позже. Однако двигать параболу можно с помощью еще одного коэффициента. 

3. Коэффициент с.

В отличие от коэффициента b, этот коэффициент отвечает за сдвиг параболы вдоль оси у. 

Его очень легко определить по графику: он будет равен точке, в которой парабола пересекает ось у. 

• Если \(c>0\), то парабола смещается вверх.
• Если \(c<0\), то парабола смещается вниз. 

На графике это будет выглядеть так: 

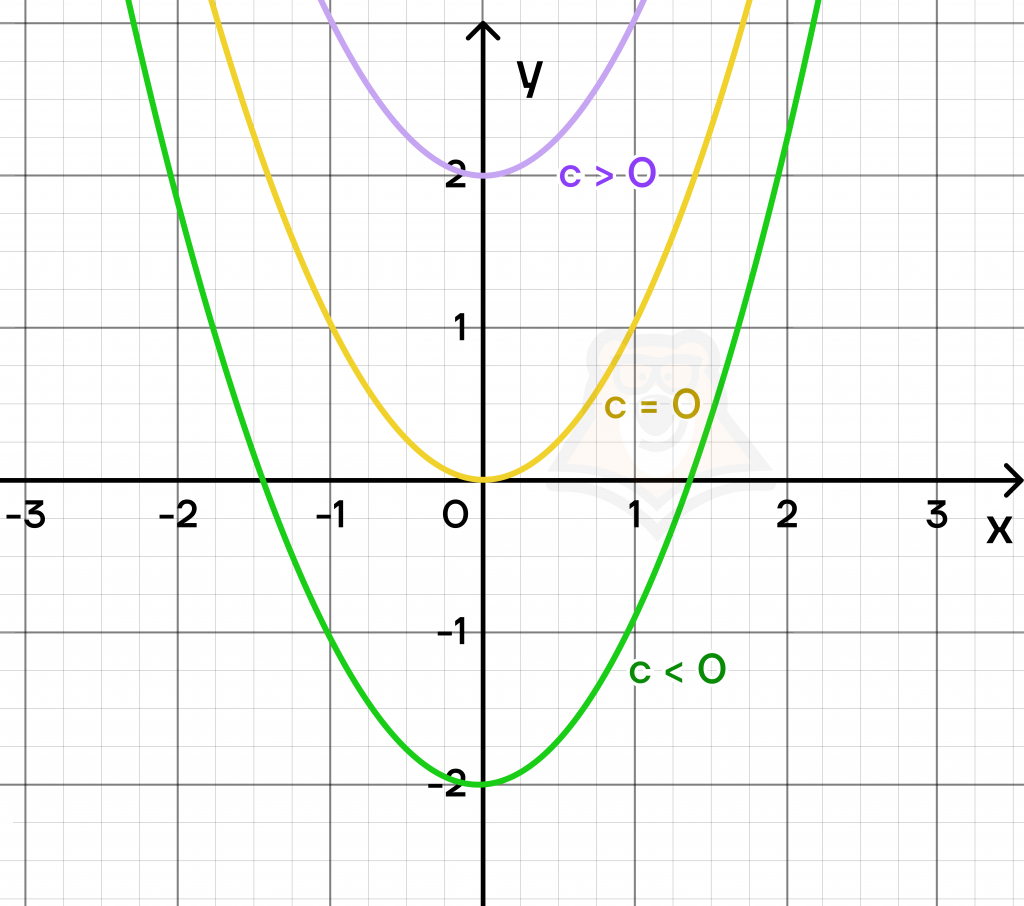
По рисунку видно, что у зеленого графика \(c=-2\), а у синего – \(c=2\). 

Параболу сложнее построить, чем остальные графики. В основном это связано с тем, что нужно знать, где ее вершина. Но есть алгоритм, который поможет построить любую параболу. 

Построение графика квадратичной функции 

Мы уже выяснили, как влияют коэффициенты на график параболы, а теперь попробуем применить эти знания. Построим график параболы \(y=x^2+2x-8\). 

Первым делом оцениваем, в какую сторону будут направлены ветви. Поскольку для данной параболы \(a>0\), то ветви направлены вверх.

Дальше нам необходимо найти координаты вершины параболы. 

Но сейчас нужно немного притормозить и вспомнить про дискриминант. Он находится по формуле:

\(D=b^2-4ac\)

Итак, что нам может рассказать дискриминант?

Как связаны дискриминант, количество решений и парабола?  Вспомним, что в зависимости от значения дискриминанта можно сделать выводы о количестве решений.  — Если \(D<0\), то решений нет. — Если \(D=0\), то уравнение имеет одно решение. — Если \(D>0\), то у уравнения два решения. Определить решения уравнения по графику очень просто: это точки пересечения с осью х. Следовательно: — Если \(D<0\), то парабола не пересекает ось х. — Если \(D=0\), то на оси х лежит вершина параболы. — Если \(D>0\), то парабола пересекает ось х в двух точках.

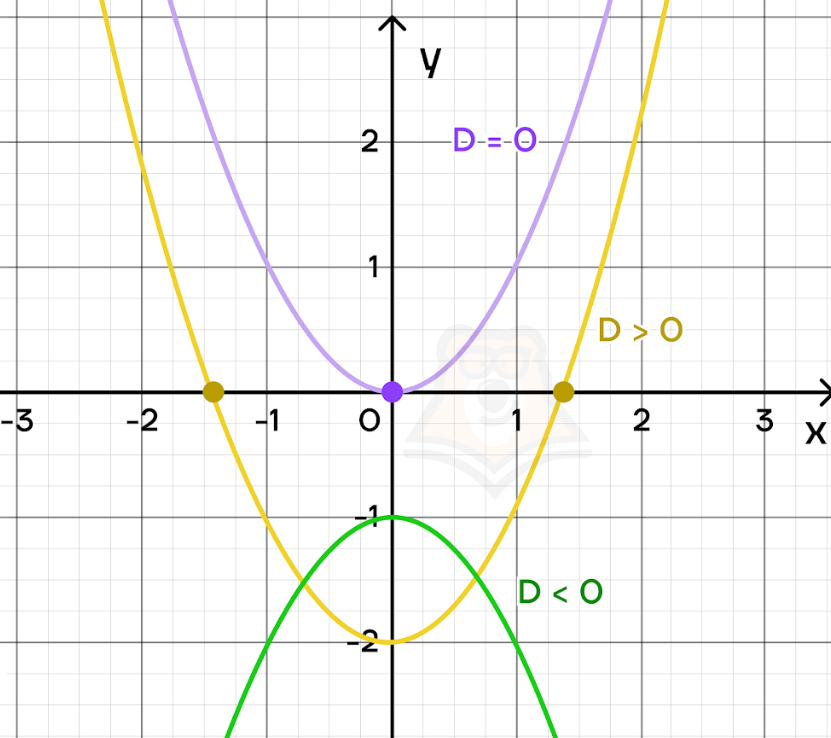
Итак, построение параболы всегда начинается с вершины. Поскольку только в вершине парабола имеет одну, а не две точки, то в ней D=0. 

Если при решении квадратного уравнения мы получаем такой дискриминант, то единственный корень можно найти по формуле:

\(x_0=\frac{-b}{2a}\)

Эта формула и будет применяться нами для нахождения абсциссы параболы. А чтобы найти ординату, необходимо будет просто подставить найденное значение х в уравнение функции. 

Теперь найдем вершину, которая задается координатами \((x_0;y_0)\): 

\(x_0=\frac{-b}{2a}=\frac{-2}{2*1}=-1\)
\(y_0=(-1)^2+2*(-1)-8=1-2-8=-9\)

Отметим вершину на координатной плоскости и проведем через нее вертикальную ось симметрии. Ветви параболы будут зеркально повторять друг друга относительно этой оси. 

Ось симметрии проводить при построении не обязательно, однако сейчас она нам необходима для наглядности.

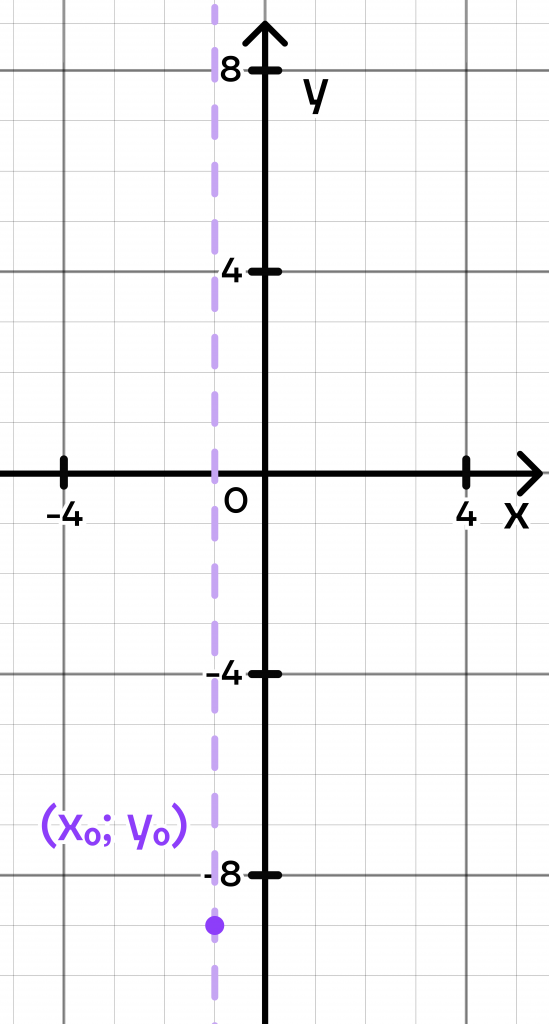
Дальше нам осталось найти еще несколько точек для построения ветвей параболы. Для 

этого составим таблицу:

х	-3	-2	0	1
у	-5	-8	-8	-5

Отметим эти точки и построим график параболы: 

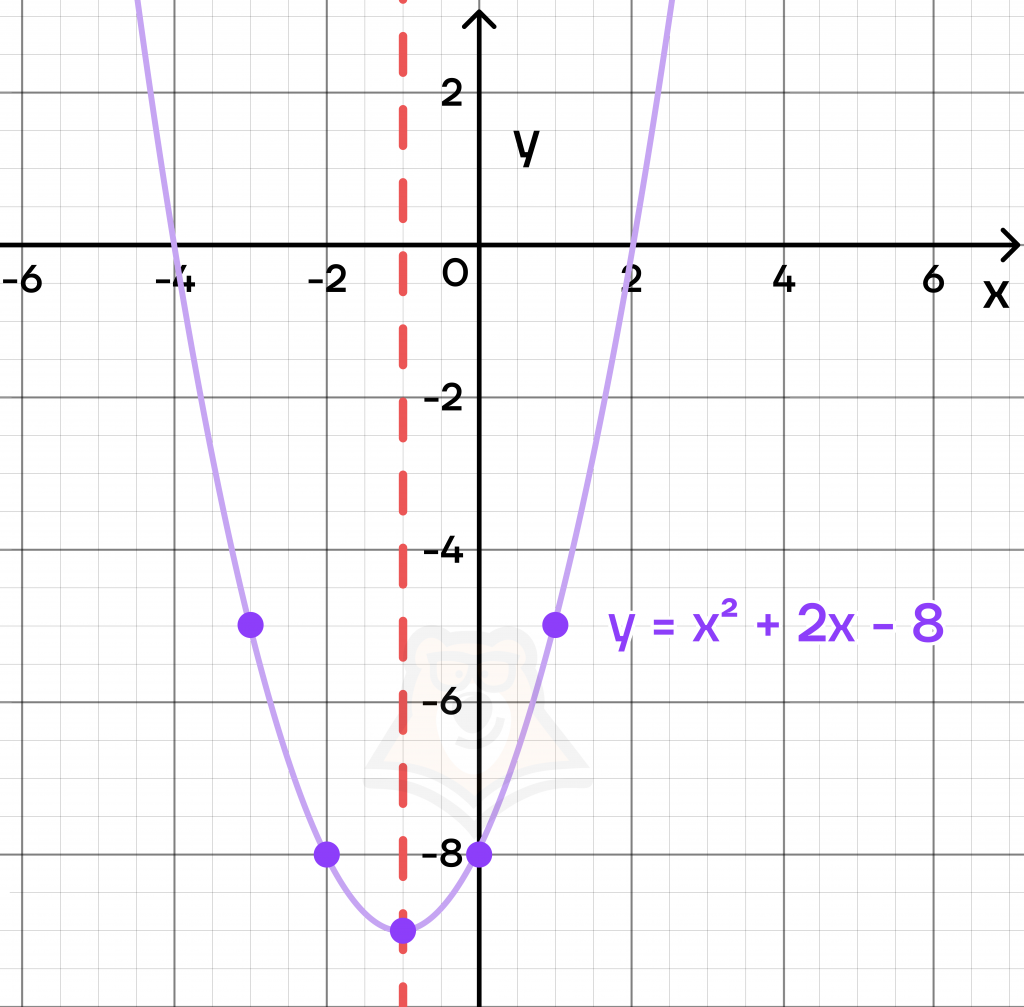
Наша парабола построена!

Алгоритм построения параболы:

1. Определить направление ветвей параболы.
2. Найти \(x_0\) по формуле \(x_0=\frac{-b}{2a}\).
3. Найти \(y_0\), подставив значение \(x_0\) в уравнение параболы.
4. Найти координаты еще нескольких точек.
5. Соединить все точки плавной линией. 

Заметим, что параболу можно построить и по трем точкам, если ее дискриминант положителен. В этом случае необходимо найти вершину параболы и нули функции (то есть точки пересечения с осью х, в этом случае \(y=0\)). 

Нам осталось только рассмотреть свойства параболы, чтобы завершить ее изучение.

Свойства квадратичной функции:

1. Область определения: \(D(y)=(-∞;+∞)\)
2. Непериодическая.
3. Нуль функции в точках пересечении параболы с осью х.

Остальные свойства зависят от каждой отдельно взятой параболы.

Знание графиков функций и формул, которыми они задаются, может пригодиться на ОГЭ по математике в №11. 

Установите соответствие между графиками функций и формулами, которые их задают.

1) \(y=-x^2+2\)
2) \(y=\sqrt x\)
3) \(y=x^3\)
4) \(y=\frac{1}{x}\)

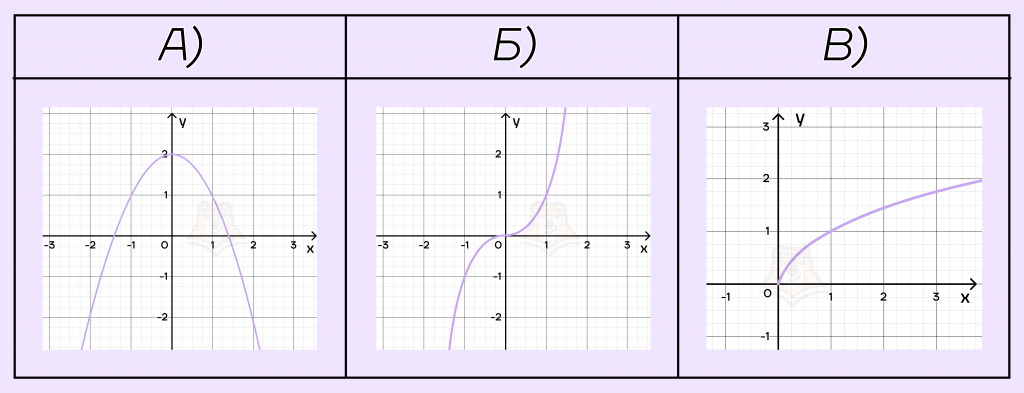
Решение.
Определим, какие функции нам даны в условии. 

1) Парабола с ветвями, направленными вниз. Ей соответствует график под буквой А.
2) Функция корня четной степени. Ей соответствует график под буквой В.
3) Степенная функция с нечетным показателем. Ей соответствует график под буквой Б.
4) Гипербола. Графика этой функции нет в условии.

Получаем соответствие:

А	Б	В
1	3	2

Ответ: 132

Мы рассмотрели основные виды функций. Но есть еще несколько!

• Про показательную и логарифмическую функции вы можете узнать из одноименной статьи. 
• О тригонометрических функциях можно узнать здесь. 
• И про еще одну важную функцию мы рассказали в статье «Модуль». 

Однако исследовать и анализировать свойства можно совершенно у любой функции. И если перед нами появится нестандартная функция, проанализировать ее можно с помощью производной, о которой вы узнаете в следующей статье. 

Термины

Асимптота – прямая, к которой неограниченно близко приближается график функции, но никогда ее не пересекает. 

Натуральные числа – числа, которые мы используем при счете, а именно целые положительные числа. Например, 1, 2, 3, 4. 

Нечетной функцией называется такая функция, график которой симметричен относительно начала координат. 

Нули функции — это значение аргумента х, при котором значение функции равно 0.

Область значений функции — это все значения, которые может принимать функция. Область значений обозначается как Е(у). 

Область определения функции — это все допустимые значения аргумента функции (то есть х), при которых функция будет определена. Область определения обозначается как D(y). 

Парабола – это незамкнутая линия, точки на которой равноудалены от оси симметрии.

Периодическая функция — это такая функция, для любого значения аргумента из области определения которой выполняется условие f(x)=f(x+T), где Т — период функции, отличный от 0. 

Показатель степени – это значение степени, в которую возводится число. 

Фактчек

• Функция корня n-ой степени задается с помощью формулы \(y=\sqrt[n]{x}, n\) – натуральное число. При этом такие функции условно можно разделить на два вида: с нечетным и четным показателем корня. 
• Если n нечетный, то функция имеет следующие свойства: область определения \(D(y)=(-\infty;+\infty)\), область значений \(E(y)=(-\infty;+\infty)\), возрастает на всей области определения, не существует ни наименьшего, ни наибольшего значения, непериодическая.
• Если n – четный, то функция имеет следующие свойства: область определения \(D(y)=[0;+\infty)\), область значений функции \(E(y)=[0;+\infty)\), наименьшее значение при \(y = 0\), непериодическая, возрастает на всей области определения.
• Степенная функция задается формулой \(y=x^a\). В зависимости от значения а функция меняет свои свойства. 
• Если а – нечетный и положительный, то область определения \(D(y)=(-\infty;+\infty)\), область значений \(E(y)=(-\infty;+\infty)\), возрастающая функция, нет ни наименьшего, ни наибольшего значения, непериодическая, нечетная функция.
• Если а – нечетный и отрицательный, то функция преобразуется в гиперболу, сохраняя ее свойства. 
• Если а – четный и отрицательный, то одна из ветвей гиперболы отзеркаливается так, чтобы весь график лежал над осью х. Такие функции имеют следующие свойства: область определения \(D(y)=(-\infty;0)\cup (0;+\infty)\), область значений функции \(E(y)=0;+\infty\), наименьшего и наибольшего значений не существует, непериодическая, возрастает на промежутке \((-\infty;0)\) и убывает на промежутке \((0;+\infty)\), четная.
• Если а – четный и положительный, то перед нами парабола. Самый часто встречающийся вид парабол – квадратичная функция, которая задается квадратным уравнением \(y=ax^2+bx+c\).
• Коэффициент а в квадратичной функции отвечает за направление ветвей и их форму, коэффициент b – за смещение параболы вдоль оси х, коэффициент с – за смещение параболы вдоль оси у.
• Чтобы построить параболу, необходимо определить направление ветвей, координаты вершины и еще нескольких точек. 

Проверь себя

Задание 1.
Как называется график функции \(y=x^{-9}\)?

1. прямая
2. кривая
3. парабола
4. гипербола 

Задание 2.
Определите какая из функций является квадратичной:

1. \(y=4(x-1)^2\)
2. \(y=2x+11\)
3. \(y=\frac{x}{2}+1\)
4. \(y=\sqrt{x}+3\)

Задание 3.
Выберите верное утверждение для функции \(y=\sqrt[5]{х}\): 

1. функция четная
2. функция нечетная
3. функция убывающая
4. функция не пересекает ось х

Задание 4.
Какая функция является функцией квадратного корня?

1. \(y=x^2\)
2. \(y=\sqrt[x-1]-4\)
3. \(y=6x+\frac{1}{3}\)
4. \(y=2x^2+3\)

Задание 5.
В какую сторону будет сдвиг у параболы \(y=x^2+8x+16\)?

1. вправо
2. вниз
3. вверх
4. влево

Ответы: 1. – 4; 2. – 1; 3. – 2; 4. – 2; 5. – 4.