Расстояния между фигурами
На этой странице вы узнаете
- Как найти расстояние между мухой и столбом?
- Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
- Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?
Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее?
Расстояния между фигурами
Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое.
Таким образом, мы получаем расстояние между двумя точками.
Расстояние между точками — это длина отрезка, заключенного между ними.

Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров.
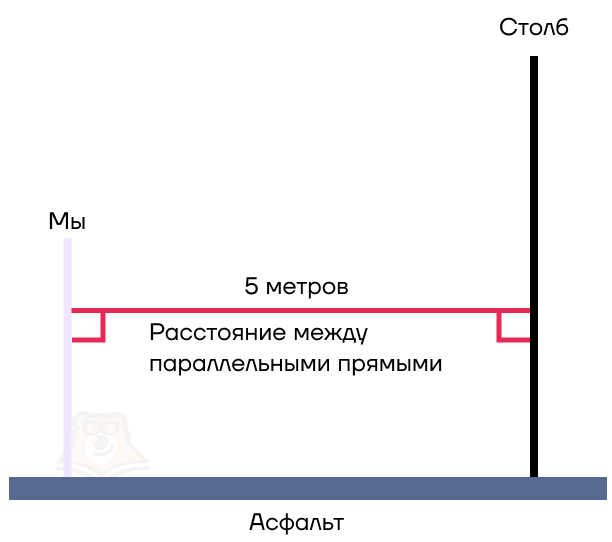
Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми.
Следовательно, мы пришли к выводу, что:
Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.
Иными словами, это отрезок, который мы прошли по асфальту.
Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление.
Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.
Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.
Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
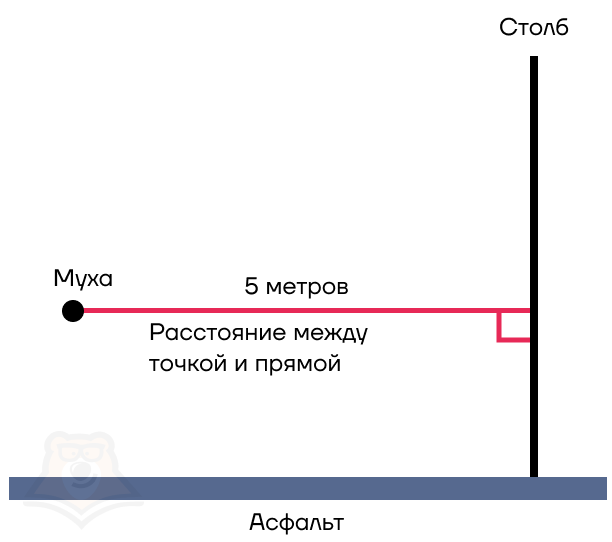
| Как найти расстояние между мухой и столбом? Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую. |
Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?
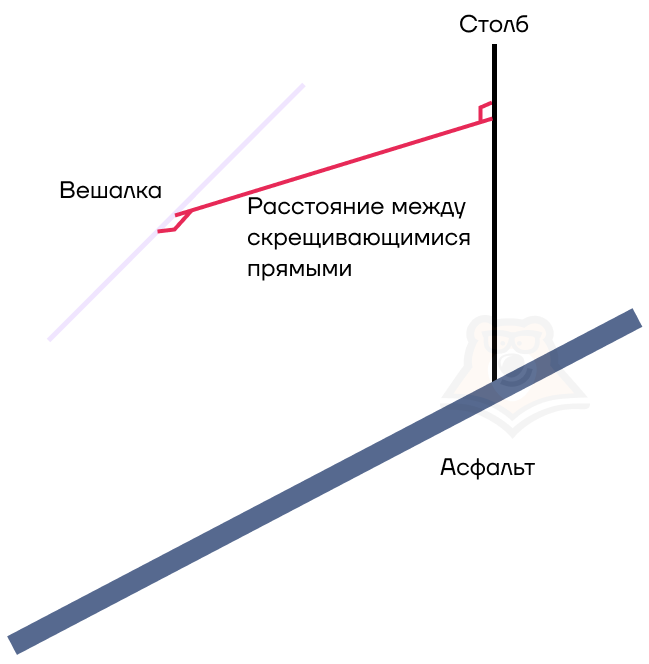
Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке.
Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии. Прямые и плоскости в пространстве».
Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай.
В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола.
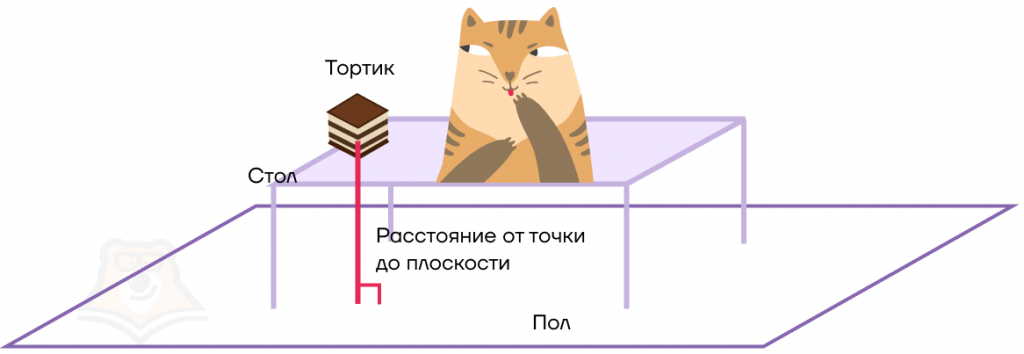
Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола.
Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.
Расстояние от рулетика до пола можно было найти и другим способом, а именно найти расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу.
Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
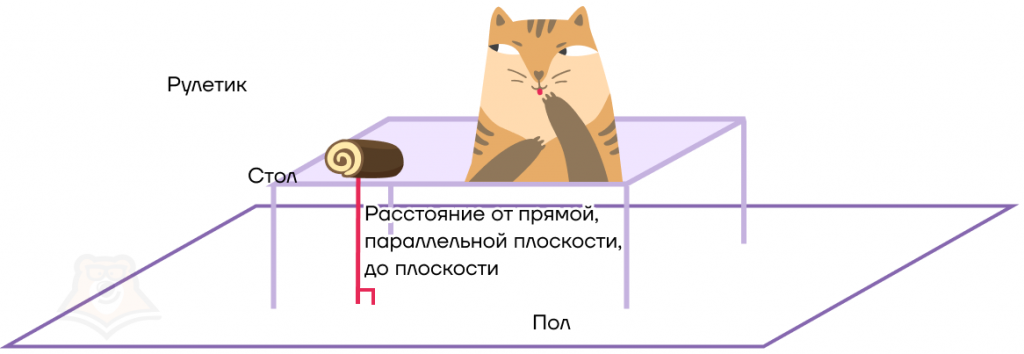
Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет.
| Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости? Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола! Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость. Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость. |
Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок.
Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике.
Теперь нам нужно найти расстояние между параллельными плоскостями.
Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
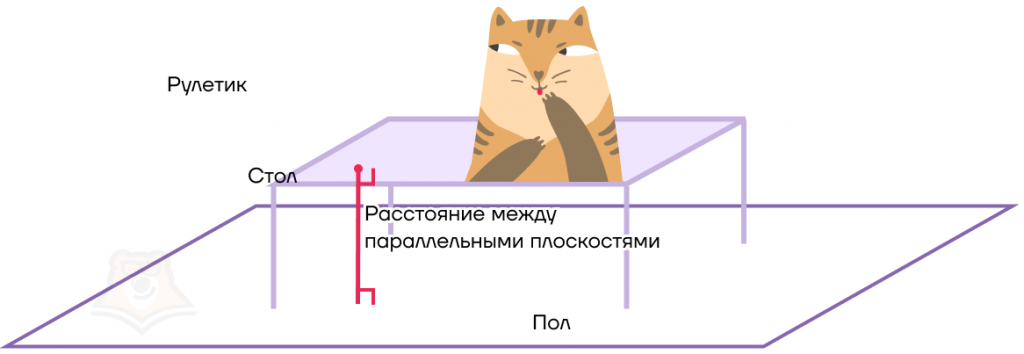
| Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом? Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость. |
Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами. Ничего сложного, верно?
При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.
Фактчек
- Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
- Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
- Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
Проверь себя
Задание 1.
Как найти расстояние между точкой и прямой?
- Найти длину любой линии от этой точки до прямой.
- Найти длину перпендикуляра, опущенного из этой точки на прямую.
- Невозможно найти расстояние между точкой и прямой.
- Ни один из вышеперечисленных вариантов.
Задание 2.
Как найти расстояние между скрещивающимися прямыми?
- Найти длину произвольной прямой между ними.
- Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
- Найти длину их общего перпендикуляра.
- Невозможно найти расстояние между скрещивающимися прямыми.
Задание 3.
Как найти расстояние от точки до плоскости?
- Найти длину перпендикуляра, опущенного из этой точки на плоскость.
- Найти длину произвольной линии, проведенной из точки к плоскости.
- Найти расстояние от точки до любой прямой, лежащей в плоскости.
- Невозможно найти расстояние между точкой и плоскостью.
Задание 4.
Как найти расстояние от прямой до плоскости?
- Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
- Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
- Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Невозможно найти расстояние между прямой и плоскостью.
Задание 5.
Как найти расстояние между параллельными плоскостями?
- Невозможно найти расстояние между параллельными плоскостями.
- Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
- Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
- Найти длину отрезка, соединяющего две произвольные прямые в плоскостях.
Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2


 к списку статей
к списку статей





