Задачи на движение

На этой странице вы узнаете

• Как задачи на движение связаны с нашей жизнью?
• Может ли быть ускорение отрицательным?
• Всегда ли можно понять, что мы плывем против течения?

Математика — не просто набор чисел и формул, она — ключ к пониманию мира вокруг нас. Добро пожаловать в захватывающий мир математики, где наши герои, Аня и Ваня, станут вашими проводниками через лабиринты задач на движение. А зачем нам знание движения? Потому что задачи на движение — это не просто абстрактные упражнения на бумаге, а своеобразные загадки, которые помогают нам справляться с повседневными ситуациями.

— Эй, Ваня, куда мы направляемся сегодня в этом мире математики?

—  Сегодня у нас в планах задачи на движение, Аня! Математика в движении, как в танце, знаешь?

— О, как интересно! Но почему бы нам не сделать шаг вперед, объяснив, почему эти задачи так важны для нашей повседневной жизни?

— Вот именно! Задачи на движение это не просто головоломки, это как навигация в реальном мире. Представь, мы можем решить, сколько времени нам понадобится, чтобы встретиться, если каждый из нас идет своим путем.

— Или рассчитать, как быстро мы сможем переплыть реку, учитывая течение воды!

— Точно! И помимо этого, задачи на движение это как наши учебники для понимания того, как работает мир вокруг нас. Не говоря уже о том, что это еще и весело!

— О, по твоим словам, Ваня, это обещает быть интересным путешествием! Надеюсь, у нас будут не только вычисления, но и немного приключений!

—Конечно!

Готовы к приключению? Давайте вместе с Аней и Ваней исследовать, почему движение — это нечто большее, чем просто перемещение из точки А в точку Б. Устраивайтесь поудобнее, включите свой математический компас, и вперед, к новым знаниям и веселым приключениям в мире задач на движение!

Введение

Задачи на движение —  это тип задач, посвященный изучению и решению задач, связанных с перемещением объектов в пространстве. 

Они позволяют моделировать и анализировать различные сценарии движения, предоставляя инструменты для определения времени, расстояний, скоростей и ускорений.

—  Но, Ваня, в чем смысл всех этих задач на движение? Зачем нам вся эта математика?

Как задачи на движение связаны с нашей жизнью? Задачи на движение играют важную роль в нашей жизни, предоставляя инструментарий для решения повседневных сценариев перемещения. Вот как они связаны с нашей жизнью. — Решение задач на движение по прямой помогает определить, когда вы встретитесь с другом, если движетесь навстречу друг другу. — Задачи на среднюю скорость могут помочь вам рассчитать оптимальное время в пути, учитывая различные скорости в разных участках маршрута. — При плавании по реке или океану задачи на движение по воде позволяют учесть течение, чтобы оптимизировать путь и время путешествия. — Задачи на нахождение скорости и ускорения тела помогут вам оценить, когда вы прибудете в место назначения, учитывая текущую скорость и изменение темпа движения. — Задачи о скорости сближения и отдаления применимы, например, при обгоне двух автомобилей на дороге, помогая предсказать момент встречи или разъезда.

—  И какие виды задач на движение существуют?

—  Есть задачи на среднюю скорость, где мы рассчитываем, сколько времени нам нужно, чтобы добраться от точки А до точки Б при различных скоростях. Затем у нас есть задачи на относительную скорость, где мы определяем, насколько быстро два объекта приближаются друг к другу или удаляются. И конечно, задачи на круговое движение, когда мы катаемся на велосипеде или вращаемся в карусели.

—  Все это звучит увлекательно!

Как вы уже поняли, задачи подразделяются на несколько видов.

• Задачи на движение по прямой. Основаны на движении объектов вдоль прямой линии. Включают в себя решение задач на встречу движущихся объектов.
• Задачи на движение по воде. Сосредоточены на движении объектов в водной среде, учитывая течение воды и другие факторы.
• Задачи на круговое движение. Определяют различные параметры движения по окружности, такие как радиус, длина дуги и угловая скорость.

Далее поговорим об основных определениях, которые помогут нам решать эти виды задач.

Основные определения

Вернемся в волнующий мир движения, где числа и формулы становятся нашими союзниками в понимании основных концепций. Для начала, давайте поговорим о трех ключевых определениях: ускорение, скорость и относительная скорость.

Скорость — это изменение положения объекта за единицу времени. 

Представим, что ваша жизнь — это путешествие на велосипеде. Скорость — это ваш спутник, определяющий, насколько быстро вы преодолеваете расстояние. 

Как найти скорость?

\(v=\frac{\Delta S}{\Delta t}\)

где \(\Delta S\) — путь, а \(\Delta t\) — время, за которое был пройден данный путь ( \(\Delta\) — изменение чего-либо)

— Аня, ты помнишь, как мы катались на велосипедах прошлым летом?

— Да, это было замечательно! Только в один момент нам пришлось вернуться домой, так как мама позвонила… 

— Да… Помню. И что мы сделали?

— Начали быстрее крутить педали.

— А зачем?

— Чтобы быстрее доехать домой.

— Верно, чем быстрее крутишь педали, тем больше скорость велосипеда. Таким образом на обратном пути мы прошли то же расстояние за меньшее количество времени.

Для решения многих задач также требуется понимание определения средней скорости. Давайте поговорим и о ней.

Средняя скорость — это отношение всего пройденного расстояния к затраченному времени. 

Средняя скорость позволяет оценить, как быстро объект проходит определенное расстояние за определенное время.

Как найти среднюю скорость?

\(v=\frac{S}{t}\)

где S — весь путь, а t — время, за которое пройден путь

Ускорение — это изменение скорости объекта со временем. 

Если вы когда-то думали, что это всего лишь физический термин, представьте себе, что ускорение — это как приготовление кофе утром, а именно тот момент, когда вы поменяли скорость мешания. Чем быстрее  мешаешь, тем быстрее кофе готов. Ускорение — это, по сути, «мешалка» для нашего движущегося объекта.

Как найти ускорение?

\(a=\frac{\delta v}{\delta t}\)

где \(\delta v\) — изменение скорости, а \(\delta t\) — время, за которое произошло изменение скорости

— Ваня, как тебе мой кофе? Я сегодня попробовала понятие ускорение… Раньше я мешала со скоростью один круг в секунду, а сейчас со скоростью два круга.

— Получается, что твое ускорение равно. Хм… два круга минус один… Получается ускорилась на один круг. Круто!

— Ускоряет твой день?

— Определенно! 

Может ли быть ускорение отрицательным? Во многих физических случаях ускорение может быть отрицательным. Отрицательное ускорение означает изменение скорости в противоположном направлении, и это происходит во множестве обыденных ситуаций. Например, когда автомобиль тормозит, его ускорение направлено в обратном направлении от движения, и это может быть представлено отрицательным числом. То есть автомобиль замедляется, скорость уменьшается, именно поэтому ускорение отрицательно.

Относительная скорость — это скорость одного объекта относительно другого.

Давайте представим, что мы смотрим на две машины с боковой дорожки — их относительная скорость определяет, насколько быстро они приближаются или удаляются друг от друга.

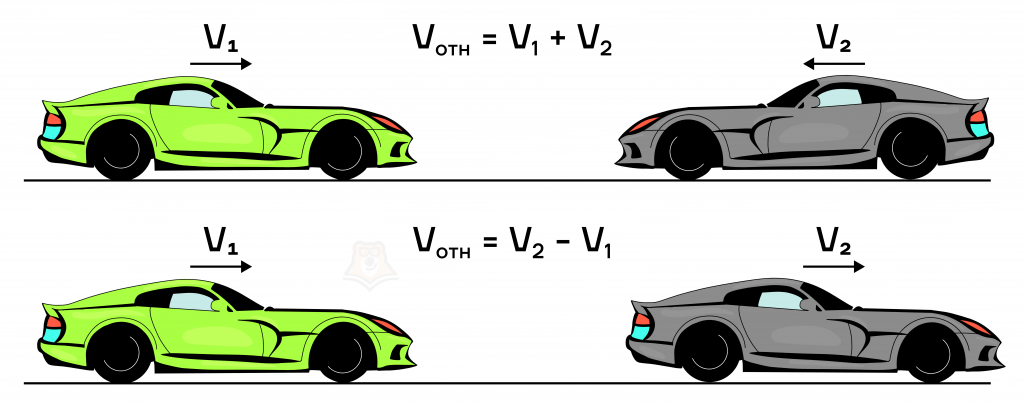
— Смотри, две машины на дороге. Одна из них едет быстро, а вторая медленно.

— Да, заметил. И что с этим делать?

— Это идеальный момент для введения концепции относительной скорости. Относительная скорость – скорость одного объекта относительно другого.

— Понял. Так что, мы просто смотрим на них и определяем, насколько быстро одна машина приближается к другой?

— Именно. Если одна машина движется со скоростью 60 км/ч, а вторая – 40 км/ч, то их относительная скорость будет 20 км/ч (60 — 40). Это покажет, насколько быстро они приближаются друг к другу или удаляются. А вот если эти машины будут двигаться навстречу друг к другу, то скорости будут складывать, то есть она будет равна  100 км/ч (60+40).

— А если они едут в одном направлении?

— Точно! Если они движутся в одном направлении, то относительная скорость будет разностью их индивидуальных скоростей. Например, если одна 60 км/ч, а вторая — 40 км/ч, то относительная скорость будет 20 км/ч (60 — 40).

Теперь, когда мы разобрались с основными определениями, можем перейти к решению задач.

Решение задач

Как мы говорили ранее, существует несколько видов задач на движение. Предлагаем начать знакомство с одним из них.

Задачи на движение по прямой

Эти задачи касаются прямолинейного движения, отражая повседневные ситуации, где объекты двигаются по прямой линии. Они позволяют нам предсказывать время встречи, оценивать расстояния и планировать перемещения. Например, если два пешехода идут друг навстречу другу с разной скоростью, задача на движение по прямой поможет определить, когда они пересекутся.

Пример.  Два велосипедиста стартовали одновременно из разных точек прямой. Первый двигается со скоростью 10 км/ч на восток, а второй —  со скоростью 8 км/ч на запад. Расстояние между ними равно 36 км. Через какое время они встретятся?

Решение. Обозначим время, которое им потребуется для встречи, как t часов.

Расстояние, которое пройдет первый велосипедист за это время, равно 10*t километров. Для второго велосипедиста это \(8*t\).

Так как они движутся друг на друга, \(10*t+8*t\) должно быть равно расстоянию между ними. Тогда \(10*t+8*t=36\)

Решая уравнение, получаем: \(18*t=36\). Из этого следует, что \(t=2\).

То есть они встретятся через 2 часа.

Ответ: они встретятся через 2 часа.

Задачи на движение по воде

Теперь представим водный мир, где течение реки или ветры на озере могут внести свои коррективы в перемещение. Задачи на движение по воде помогут нам оценивать, как изменения в окружающей среде влияют на наше плавание или движение судна. Как, например, определить, сколько времени займет переплытие реки, если учесть течение в расчетах?

Очевидно, течение влияет на скорость движения объектов в воде. 

• Когда объект движется вдоль направления течения, скорость течения прибавляется к скорости объекта, увеличивая его общую скорость. Это называется движение «по течению». 
• Напротив, когда объект движется против направления течения, скорость течения вычитается из скорости объекта, что уменьшает его общую скорость. Это называется движение «против течения».

Что касается плота, его скорость относительно воды обычно равна скорости течения, когда он движется вдоль течения. Это означает, что скорость плота относительно берега идентична скорости течения, но это не учитывает влияние ветра, течения воздуха или других факторов, влияющих на движение судна.  

Всегда ли можно понять, что мы плывем против течения? Когда речь идет о водных потоках, то можно однозначно определить, плывет ли что-то против течения. Вода, как правило, имеет определенное направление и скорость течения, которые обычно можно наблюдать или измерить. Однако, некоторые факторы, такие как приливы, ветер или изменения в рельефе дна, могут усложнить определение того, движется ли что-то против течения. Например, в реке или потоке можно заметить водные вихри, которые могут служить индикаторами того, что что-то движется против направления течения. Глубокие участки вдоль берега или определенные преграды также могут создавать участки, где течение идет медленнее, что может создать впечатление, будто что-то движется против течения. Таким образом, в случае водных потоков можно сказать, что в большинстве случаев можно определить, движется ли что-то против течения, однако существуют факторы, которые могут затруднить такую оценку.

Пример. Лодка движется против течения реки со скоростью 15 км/ч, а течение имеет скорость 5 км/ч. Какова скорость лодки относительно берега?

Решение. Относительная скорость лодки относительно берега равна разности их скоростей. Таким образом, это \(15-5=10\) (км/ч).

Ответ: Скорость лодки относительно берега составляет 10 км/ч.

Решим задание, которое может встретиться на ОГЭ по математике в задании №21.

Задание. Пристани A и B расположены на реке, скорость течения которой на этом участке равна 2 км/ч. Лодка проходит туда и обратно без остановок с собственной скоростью 8 км/ч. Найти среднюю скорость лодки.

Решение. Обозначим собственную скорость лодки за \(v_{лодки}\) км/ч, а скорость течения реки \(v_{теч}\) км/ч
Когда лодка плывет по течению, то она движется со скоростью: 

\(v1 = v_{лодки} + v_{теч}=(8+2) км/ч = 10\) км/ч

Когда лодка плывет против течения, то она движется со скоростью: 

\(v2 = v_{лодки} — v_{теч}=(8-2) км/ч = 6\) км/ч

Мы хотим найти среднюю скорость. Давайте распишем ее, приняв за расстояние между пристанями A и B величину S:

\(v_{ср}=\frac{S}{t}=\frac{S}{S/v1+S/v2}\)

Мы также нашли суммарное время, которое лодка затратила на путь туда и обратно. Тогда получим:

\(v_{ср}=\frac{S}{t}=\frac{S}{S/10+S/6}=\frac{1}{1/10+1/6}=\frac{1}{6/60+10/60}=\frac{1}{\frac{16}{60}}=\frac{60}{16}=3,75\) км/ч(S при решении сократилось на начальном этапе)

Ответ: 3,75 км/ч.

Задачи на нахождение скорости и ускорения тела

В этой задаче мы погружаемся в мир динамики, где ускорение и скорость становятся ключевыми игроками. Предположим, вы на велосипеде, начинающем движение с нулевой скорости. Задача на нахождение скорости и ускорения тела поможет вам разобраться в динамике вашего движения, а может быть, и предсказать, как быстро вы разгонитесь.

— Я нашла интересную задачу на нахождение скорости и ускорения тела. Ты готов покопаться в числах?

— Конечно, давай посмотрим, что у нас тут. Какая задача?

— Представь, у нас есть мотоциклист, который стартует со скоростью 20 м/с и ускоряется равномерно. Через 10 секунд его скорость становится 30 м/с. Мы хотим найти его ускорение. 

— Отлично, давай вспомним формулу ускорения. Это изменение скорости деленное на время.

— Именно! Так что, как мы можем применить эту формулу к нашей задаче?

— Посмотрим, у нас начальная скорость равна 20 м/с, конечная скорость равна 30 м/с, и время 10 секунд. Подставим значения и найдем ускорение. 

— Великолепно! Поехали, математический мотоциклист!

— Хорошо. Ищем ускорение: \(\frac{30-20}{10}=1\) (\(м/c^2\)). Итого получаем, что ускорение равно 1.

— Вау, мы справились! У нас есть ответ. Теперь этот мотоциклист не так прост, как кажется.

По своей сути эти задачи похожи на все те, что мы рассмотрели. Так как решение одинаково, но нужно найти другую величину.

Задачи на среднюю скорость

Представим себе ситуацию путешествия, когда наш маршрут включает различные участки с разными скоростями. Задачи на среднюю скорость помогут нам определить общую скорость нашего путешествия, учитывая все эти изменения темпа. Как, например, рассчитать среднюю скорость автомобиля, двигавшегося с разной скоростью на горных и равнинных участках дороги?

Пример. Автомобиль двигается со скоростью 40 км/ч в течение первых 2 часов и со скоростью 60 км/ч в течение следующих 3 часов. Найти среднюю скорость за всю поездку.

Решение. Средняя скорость рассчитывается как общее расстояние, деленное на общее время. Общее расстояние – это сумма расстояний на первой и второй части пути, а общее время —  это сумма времени на обеих частях пути.

Давайте для начала найдем общее расстояние. Оно складывается из произведения скоростей на время, в течение которого автомобиль сохранял эту скорость. Тогда получаем: \(S = 40*2 + 60*3\)

Средняя скорость: \(\frac{40*2+60*3}{2+3}=\frac{80+180}{5}=52\) (км/ч)

Решая, получаем среднюю скорость.

Ответ: средняя скорость за всю поездку равна 52 км/ч

Задачи, использующие скорость сближения и скорость отдаления

Задачи о скорости сближения и отдаления становятся актуальными в ситуациях встречи или разъезда двух объектов. Давайте представим себе два поезда, движущихся друг на друга, и задача заключается в том, чтобы вычислить, как быстро они сблизятся. 

Задачи, использующие скорость сближения и скорость отдаления относятся к задачам на относительную скорость. Именно о них мы поговорим далее. 

Задачи на относительную скорость

Относительная скорость — наш математический инструмент в анализе взаимодействия двух объектов. Задачи на относительную скорость помогут нам понять, насколько быстро они приближаются или удаляются друг от друга. В контексте, например, двух лодок, движущихся в разных направлениях по реке, эти задачи позволяют нам предсказывать момент встречи или разъезда.

Пример. Допустим, два велосипедиста начинают движение одновременно из двух разных точек города, один велосипедист едет со скоростью 20 км/ч на север, а другой со скоростью 15 км/ч на юг. Расстояние между их точками старта 70 км. Найдем время, через которое они встретятся, а также расстояние, которое каждый из них проедет.

Решение. Подобную задачу мы уже решали. Мы точно знаем, как найти время, через которое они встретятся. Напишем сразу уравнение: \(20*t+15*t= 70\). Тогда \(t=2\).

То есть они встретятся через 2 часа в одной точке. Найдем расстояние, который проедет каждый из них:

Первый пройдет \(20*t=20*2=40\) км.

Второй пройдет \(15*t=15*2=30\) км.

Ответ: Они встретятся через 2 часа. Первый пройдет 40 км, а второй 30 км.

Задачи на круговое движение

Наконец, перейдем к захватывающему миру кругового движения. Задачи на круговое движение помогают понять, как объекты вращаются вокруг центра. Представим себе бегуна, который бежит круги по полю. Мы можем найти, например, скорость, зная, сколько кругов он побежал, какое количество времени ему понадобилось.

Пример. Представим, что бегун бежит вокруг стадиона радиусом \(\frac{960}{\pi}\) метров. Скорость бегуна составляет 4 м/с. Найдем, сколько целых кругов он пробежит за 6 минут.

Решение. Для начала определим, какое расстояние пробежит бегун. Оно равно скорости, умноженной на время. Важно отметить, что время дано в минутах, его нужно перевести в секунды: \(S=4*(6*60)=1440\) (м).

Давайте найдем длину окружности (то есть длину маршрута, когда бегун пробегает 1 круг): \(L_{круга}=2*\pi *r=2*\pi *\frac{960}{\pi}=1920\) (м).

Количество кругов, которое пробежит бегун за 6 минут равно расстоянию, которое бегун пробежал, деленное на расстояние одного круга: \(\frac{1440}{1920}=0,75\). То есть стадион настолько большой, что бегун не успеет пробежать 1 круг. Поэтому ответ 0.

Ответ: бегун пробежит 0 целых кругов.

Решим задание, которое может встретиться на ЕГЭ по математике в задании №10.

Задание. Из одной точки круговой трассы, длина которой равна 16 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение. Пусть скорость второго автомобиля равна v км/ч. За 40 минут (2/3 часа) первый автомобиль прошел на 16 км больше, чем второй, так как один круг равен 16 км по условию. Составим уравнение:

\(80*\frac{2}{3}=v*\frac{2}{3}+16 |*3\)
\(80*2=v*2+16*3\)
\(160=v*2+48\)
\(v*2=160-48=112\)
\(v=\frac{112}{2}=56\) (км/ч) 

Ответ:  56 

— Вот и последняя задача решена! Математика оказывается повсюду.

— Да уж, Аня, и задачи на движение — отличный пример того, как мы можем использовать математику для понимания мира вокруг нас.

— Верно! Решение этих задач помогает не только развивать наши математические навыки, но и применять их в реальных ситуациях, будь то путешествие на автомобиле или даже бег по парку.

— И не забывай, что математика — это не только серьезные вычисления, но и увлекательное приключение!

Мы рассмотрели основные принципы решения различных видов задач на движение, ознакомились с определениями и примерами, которые помогли глубже понять эту важную тему. Приглашаем вас познакомиться с не менее интересной статьей «Действия с натуральными числами» и окунуться в мир математики. До новых встреч!

Фактчек

• Задачи на движение — это математические задачи, связанные с описанием и анализом движения объектов в пространстве. Они требуют использования концепций скорости, ускорения и расстояния для решения практических сценариев.
• Скорость — отношение пройденного расстояния к затраченному времени. 
• Ускорение — изменение скорости объекта за единицу времени.
• Относительная скорость — скорость одного объекта относительно другого.
• Виды задач на движение: движение по прямой, движение по воде, круговое движение.
• Практическое применение: оптимизация времени и расстояний при движении, анализ движения тел в пространстве, расчет траекторий и скоростей.

Проверь себя

Задание 1.
Автомобиль стартует из точки А и движется со скоростью 40 км/ч. Через сколько времени он достигнет точки В, находящейся на расстоянии 120 км от точки старта?

1. 2 часа
2. 3 часа
3. 4 часа
4. 5 часов

Задание 2.
Поезд движется со скоростью 60 км/ч, а автомобиль – со скоростью 80 км/ч, причем оба в одну сторону.. Какова относительная скорость между ними?

1. 20 км/ч
2. 40 км/ч
3. 60 км/ч
4. 80 км/ч

Задание 3.
Велосипедист проезжает полный круг вокруг парка длиной 2 км за 30 минут. Какова его средняя скорость?

1. 2 км/ч
2. 4 км/ч
3. 6 км/ч
4. 8 км/ч

Задание 4.
Лодка движется по течению реки со скоростью 15 км/ч. Если скорость течения реки 5 км/ч, какова скорость лодки относительно берега?

1. 10 км/ч
2. 15 км/ч
3. 20 км/ч
4. 25 км/ч

Ответы: 1. — 2 ; 2. — 1; 3. — 2; 4. — 3.