Решение задач с параметром методом исследовательского анализа
На этой странице вы узнаете
- Категоричность или лояльность: чем отличается система от совокупности?
- Как проходит борьба за первенство между переменными?
- Как выглядят неравенства на графиках функций?
Как бы нам ни хотелось обратного, но научиться решать задачи с параметром, прочитав краткую инструкцию и выписав несколько формул, не получится. Нам обязательно потребуется аналитическое мышление, то есть способность разбивать информацию на небольшие части, исследовать и делать выводы. Узнаем об этом в статье.
Системы уравнений с параметром
Что мы представляем, когда говорим про аналитику? Возможно, серьезных мужчин и женщин, которые много думают, сравнивают данные и делают на их основе сложные прогнозы. Они в строгих костюмах и очках, с серьезным сосредоточенным лицом.

Мы предлагаем погрузиться в аналитику в параметрах. По желанию надеваем серьезный костюм и очки, и вперед.
Немного организационных вопросов перед нашим путешествием. Что подразумевает под собой аналитический способ решения параметров? В первую очередь, это использование алгебраических преобразований и рассуждений без привлечения графиков. Про графический способ решения параметров можно прочесть в отдельной статье.
Как можно преобразовать системы уравнений? Рассмотрим пример.
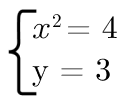
Решим первое уравнение системы, получаем, что x=2 или
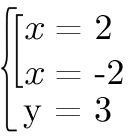
Что мы можем сказать про совокупность и про систему? Совокупность, которая обозначается квадратной скобкой, выполняется в случае, если выполняется хотя бы одно, любое из ее уравнений. Чтобы выполнялась система, необходимо, чтобы выполнялись все условия, которые в нее включены.
| Категоричность или лояльность: чем отличается система от совокупности? Представим, что система и совокупность — это две дамы. Система будет дамой категоричной. Ни одно из ее слов или условий не должны быть пропущены, иначе она обидится и не будет с нами сотрудничать. А вот совокупность — дама лояльная. Она может простить, если не все ее условия выполнены. Для нее главное — понять, что мы ее слушали. А как это сделать? Выполнить хотя бы одно из поставленных ей условий. |
Назовем уравнение y = 3 Кристиной. Кристина очень любит вязаных жабок (x = 2) и плюшевых ленивцев (x = — 2). Предположим, что Кристина пошла в магазин, чтобы купить новую игрушку. Скорее всего, она купит именно те игрушки, которые ей нравятся, поэтому система
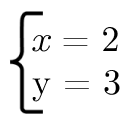
будет обозначать, что Кристина купила жабку, которую очень любит.
А вот система
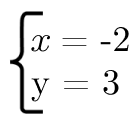
означает, что Кристина купила ленивца, которого также очень любит.
Разумеется, она может купить и жабку, и ленивца. Но что, если в магазине не будет одной из этих игрушек или у Кристины не хватит денег? Она купит только одну из них. А как показать это на языке математики? Совокупностью из двух систем:
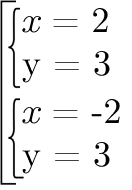
Эта совокупность будет выполняться, даже если Кристина купит только жабку или только ленивца.
Так можно преобразовать любую систему или совокупность. Например, рассмотрим преобразование системы из двух совокупностей:
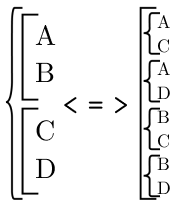
Переведем с языка математики. Нам было нужно, чтобы одновременно выполнялось А или В и С или D, то есть хотя бы по одному условию из каждой совокупности. Нам была необходима ситуация (А или В) и (С или D).
Следовательно, если выполняется условие А, то обязательно должно выполняться и условие С или D. Образуются две системы: “А и С” или “A и D”. Если выполняется условие В, то обязательно должно выполняться условие C или D, получаются две системы: “В и С” или “В и D”.
Для выполнения самой первой системы нужно выполнение хотя бы одной из получившихся четырех систем. Тем самым мы получаем совокупность из четырех систем: (А и С) или (А и D) или (В и С) или (В и D).
Решение систем уравнений на примере
Рассмотрим на примере, как можно решить систему уравнений. Для этого запасемся терпением, подготовим наши блокноты и ручки и начнем погружение в мир аналитики.
Пример 1. Найдите все значения параметра а при каждом из которых система уравнений имеет ровно 4 решения.
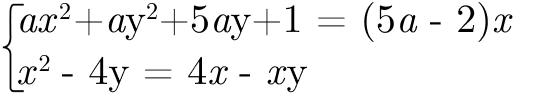
Решение.
Шаг 1. Проанализируем второе уравнение системы и попробуем преобразовать его. Перенесем все слагаемые в одну сторону:
x^2-4y-4x+xy=0
Вынесем общие множители за скобку:
x(x-4) + y(x-4)=0
(x+y)(x-4)=0
Если произведение двух множителей равно 0, то каждый множитель равен 0. Следовательно, решением этого уравнения будет совокупность
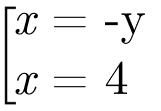
Шаг 2. Получаем систему из уравнения и совокупности. Преобразуем ее рассмотренным ранее способом.

Шаг 3. Вспомним, что сейчас мы аналитики и попробуем определить, в каких случаях у совокупности будет четыре решения.
Представим, что у нас есть две двухрублевые монеты. Как сделать из них четыре монеты? Разменять каждую двухрублевую монету на две однорублевые.
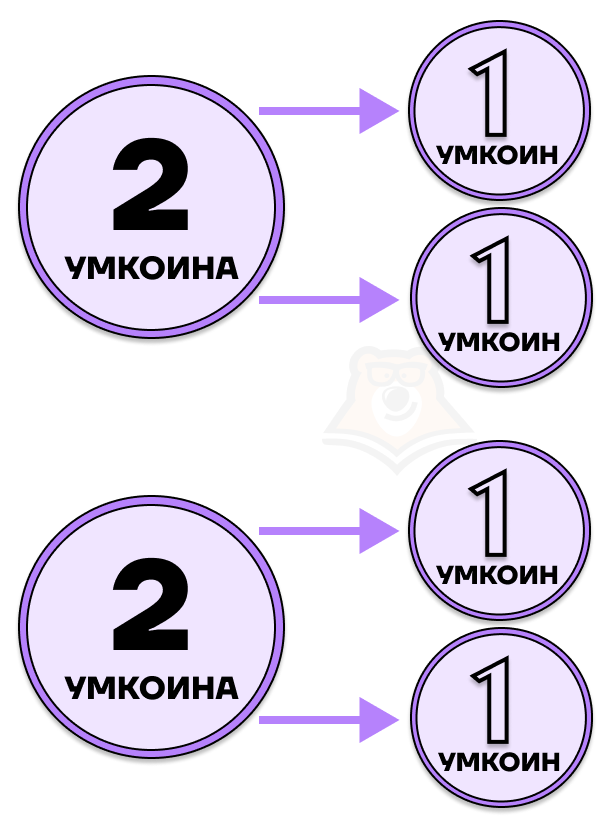
Шаг 4. Нам необходимо, чтобы в совокупности каждая система имела ровно два решения.
Шаг 5. В каких случаях у квадратного уравнения будет два решения? Если коэффициент перед x2 не будет равен 0. В уравнении
ax^2 + ay^2 + 5ay + 1 = (5a-2)x
получаем, что a ≠ 0.
Проверим. Для этого подставим значение a = 0 в совокупность:
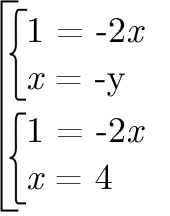
Из первого уравнения системы получаем, что
x=-\frac{1}{2}Тогда решением первой системы будет точка
(-\frac{1}{2};\frac{1}{2})— единственное решение.
Во второй системе решений не будет, поскольку при x = 4 не выполняется равенство 1 = — 2 * 8. Всего будет одно решение, что не подходит к условию.
Шаг 6. А что будет, если уравнения x = — y и x = 4 совпадут? У нас получится совокупность из двух совершенно одинаковых систем. Их решения совпадут, то есть их будет не 4, а 2.
Таким образом, мы получаем новое условие:
— y ≠ 4 => y ≠ -4 при x = 4. То есть точка (4; -4) не может быть решением.
Найдем, чему равен параметр в этом случае, для этого подставим значения x и y в первое уравнение:
a * 4^2+a * (- 4)^2 + 5a(- 4) + 1 = (5a - 2)4
16a + 16a - 20a + 1 = 20a - 8
8a = 9
a=\frac{9}{8}Следовательно,
a≠\frac{9}{8}Шаг 7. Теперь рассмотрим отдельно каждую из двух систем и найдем, при каких значениях параметра а они будут иметь по два решения.
В первое уравнение первой системы подставим x = — y, получаем:
a(- y)^2 + ay^2 + 5ay + 1 = (5a - 2)(- y)
2ay^2 + 5ay + 1 + 5ay - 2y = 0
2ay^2 + y(10a - 2) + 1 = 0
Мы получили обычное квадратное уравнение. Оно будет иметь два решения, если его дискриминант будет строго больше 0:
D = (10a - 2)^2 - 4 * 2a * 1 = 100a^2 - 40a + 4 - 8a = 100a^2 - 48a + 4
D > 0 => 100a^2 - 48a + 4 > 0
Решая неравенство «Методом интервалов», получаем, что
a\in(-\infty;\frac{6-\sqrt{11}}{25})\cup(\frac{6+\sqrt{11}}{25};+\infty)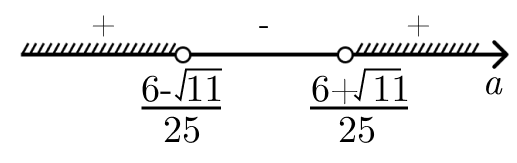
Шаг 8. Аналогично решаем вторую систему.
Подставим х = 4 в первое уравнение системы:
a * 4^2 + ay^2 + 5ay + 1 = (5a - 2) * 4
16a + ay^2 + 5ay + 1 = 20a - 8
ay^2 + 5ay + 9 - 4a = 0
Чтобы у этого уравнения было два решения, его дискриминант должен быть строго больше 0.
D = 25a^2 - 4a *(9 - 4a) = 25a^2 - 36a + 16a^2 = 41a^2 - 36a = a(41a - 36)
D > 0 => a(41a - 36) > 0
Решаем неравенство методом интервалов и получаем, что a
a\in(-\infty;0)\cup(\frac{36}{41};+\infty)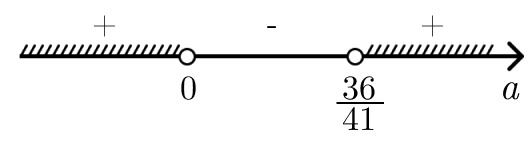
Шаг 9. В этот момент нам, как аналитикам, необходимо задуматься: а как объединить эти решения? Брать все получившиеся значения а или только те, которые удовлетворяют каждому из интервалов?
Представим, что нам нужно организовать праздник, на который придут два друга. Мы точно знаем, что один из них пьет только апельсиновый сок, а второй только апельсиновый или яблочный соки. Какой сок мы купим, чтобы все были довольны? Апельсиновый.
Точно также и здесь: чтобы обе системы были “довольны” и имели по два решения, нужно, чтобы все значения параметра а удовлетворяли условиям каждой из систем. Поэтому нам необходимо найти пересечение этих решений.
Шаг 10. Заметим, что
\frac{6-\sqrt{11}}{25}>\frac{6-\sqrt{36}}{25}Cледовательно,
\frac{6-\sqrt{11}}{25}>0\frac{36}{41}>\frac{6+\sqrt{11}}{25}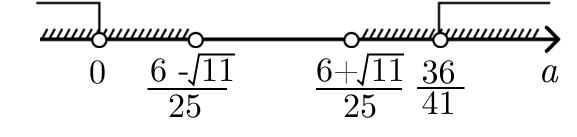
Получаем, что
a\in(-\infty;0)\cup(\frac{36}{41};+\infty)Шаг 11. Не забудем, что
a≠\frac{9}{8}эту точку также нужно выколоть из ответа.
Получаем:
a\in(-\infty;0)\cup(\frac{36}{41};\frac{9}{8})\cup(\frac{9}{8};+\infty)Ответ:
a\in(-\infty;0)\cup(\frac{36}{41};\frac{9}{8})\cup(\frac{9}{8};+\infty)Выдохнем и вытрем испарину со лба: параметр решен. Если исключить достаточно трудоемкие вычисления, то остается только немного порассуждать.
А бывает ли так так, что параметр выступает как равноправная переменная? Давайте ответим на этот вопрос.
Параметр как равноправная переменная
В рассмотренных ранее случаях параметр был темной лошадкой: он почти постоянно был на фоне, появлялся только под конец, чтобы внести свой вклад и показать свои способности, то есть значения. Но что, если вывести параметр на первый план?
Рассматривая функции, мы привыкли, что у — значение функции, которое зависит от переменной х. Однако в некоторых задачах с параметром от переменной х может зависеть и сам параметр.
В этом случае в борьбе между “у” и “а” выигрывает параметр и занимает место у. То есть параметр будет вести себя точно так же, как обычная функция, а изменение значения х будет менять и значение параметра.
Разумеется, можно построить и график такой функции, просто ось ординат будет подписана как “а”, а не “у”.
А может ли быть наоборот? Да. Параметрическую плоскость хОа можно использовать в двух случаях:
- параметр а — зависимая переменная, х — независимая;
- х — зависимая переменная, параметр а — независимая.
Как определить, какой из случаев использовать в конкретном примере? Нужно посмотреть, каким способом удобнее выразить одну переменную через другую. Например, в уравнении x2 + 5x — a = 0 намного удобнее выразить значение параметра a = x2 + 5x, чем пытаться вывести значение х. В этом случае мы получим параболу. Подробнее про параболу можете узнать в статье «Основные элементарные функции».
| Как проходит борьба за первенство между переменными? Между переменными в уравнениях всегда идет “борьба”: кто будет зависимой переменной, а кто независимой. Поскольку мы смотрим, с кем будет удобнее работать в качестве зависимой переменной, то сами выбираем победителя схватки. |
Когда можно прибегнуть к такому методу решения параметров? Обычно его используют, если в уравнении, неравенстве или их системах есть только две переменные, одна из которых является параметром.
Пример 2. Найдите все значения параметра а, при которых система имеет хотя бы одно решение на промежутке [-3;1].
Решение. Если посмотреть на второе неравенство системы, то заметно, что удобнее выразить параметр через переменную х. Поэтому при решении параметр будет зависимой переменной, а х — независимой.
Шаг 1. Разберем первое неравенство системы и раскроем модули четырьмя способами. Подробнее про модули можно узнать в статье «Модуль». Также в дальнейшем будем использовать графический способ решения параметров.
x\geqslant0;a\geqslant0 => x+a\leqslant7=>a\leqslant7-x
Дальше мы отойдем от аналитического метода решения и будем решать графически, так как иногда такое решение будет проще и быстрее.
Рассмотрим, как все условия будут выглядеть на графике.
x\geqslant0
— плоскость, которая включает все значения х, больше 0.
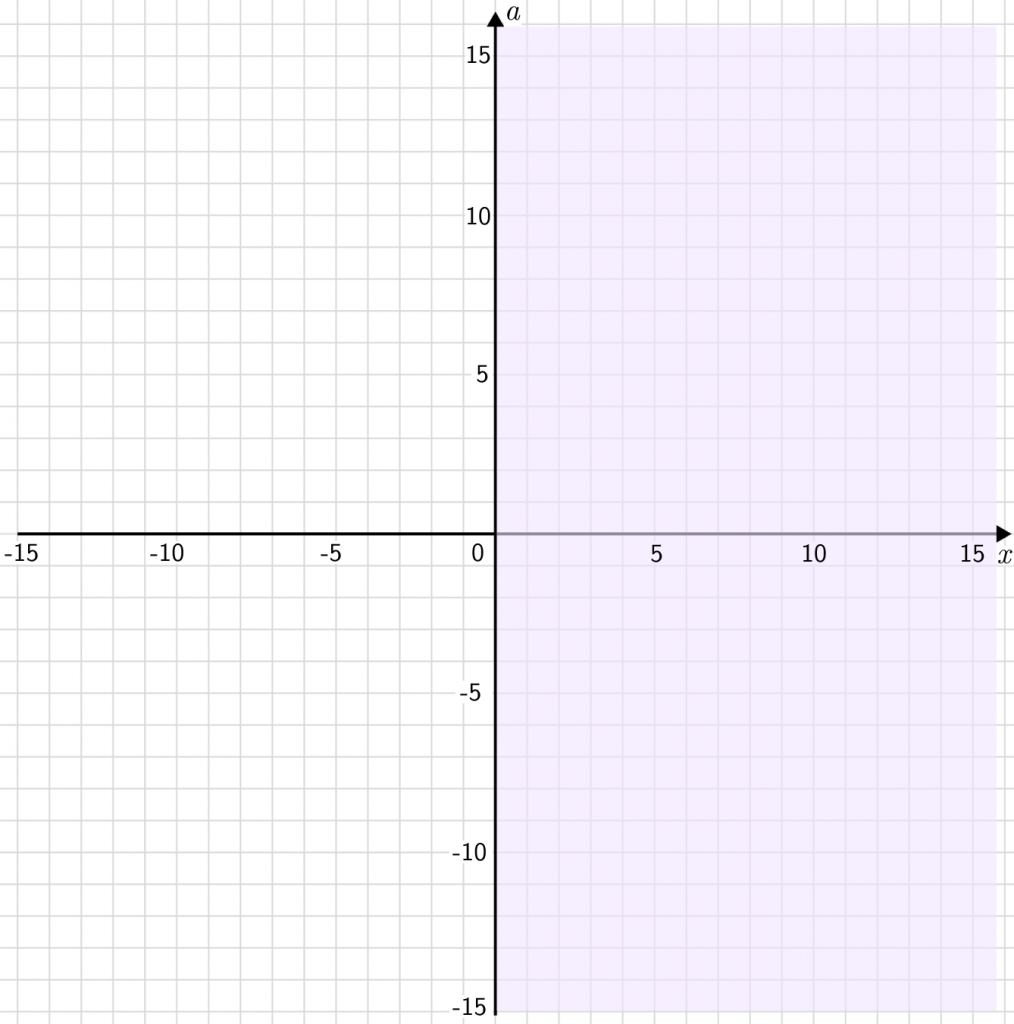
a\geqslant0
включают все точки, которые лежат выше линии а = 0.
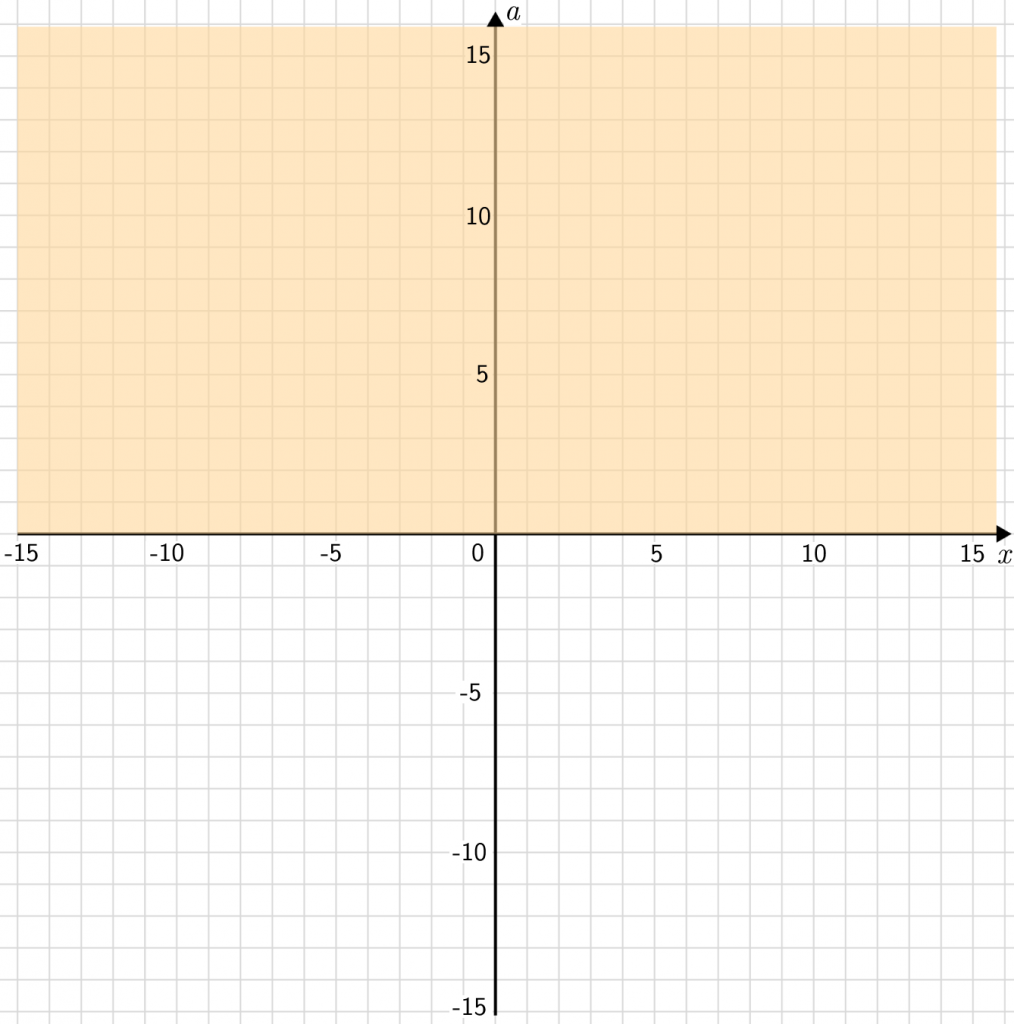
А неравенство
a\leqslant7-x
включает все, что лежит ниже прямой 7 — x.
То есть каждый раз мы как бы разрезаем плоскость по одной из линий и отбрасываем все, что не удовлетворяет условию.
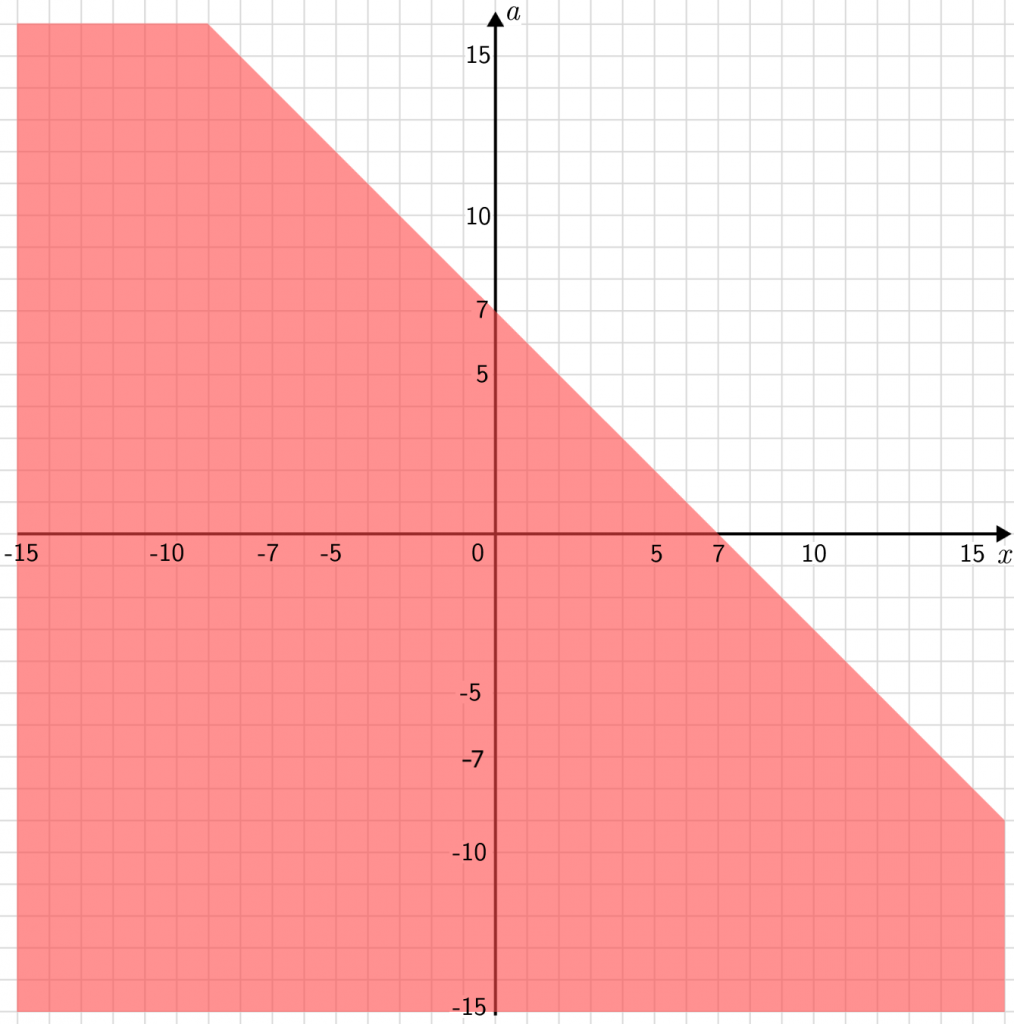
| Как выглядят неравенства на графиках функций? В отличие от графиков обычных уравнений, неравенства задают не линию, а часть плоскости. То есть его решению будут удовлетворять все точки, которые попадут в нужную часть плоскости. Неравенства очень жадные: они забирают себе не только точки, которые принадлежат определенной линии, но и все точки, которые лежат выше или ниже. |
Наложим все три условия друг на друга и найдем место их пересечения.
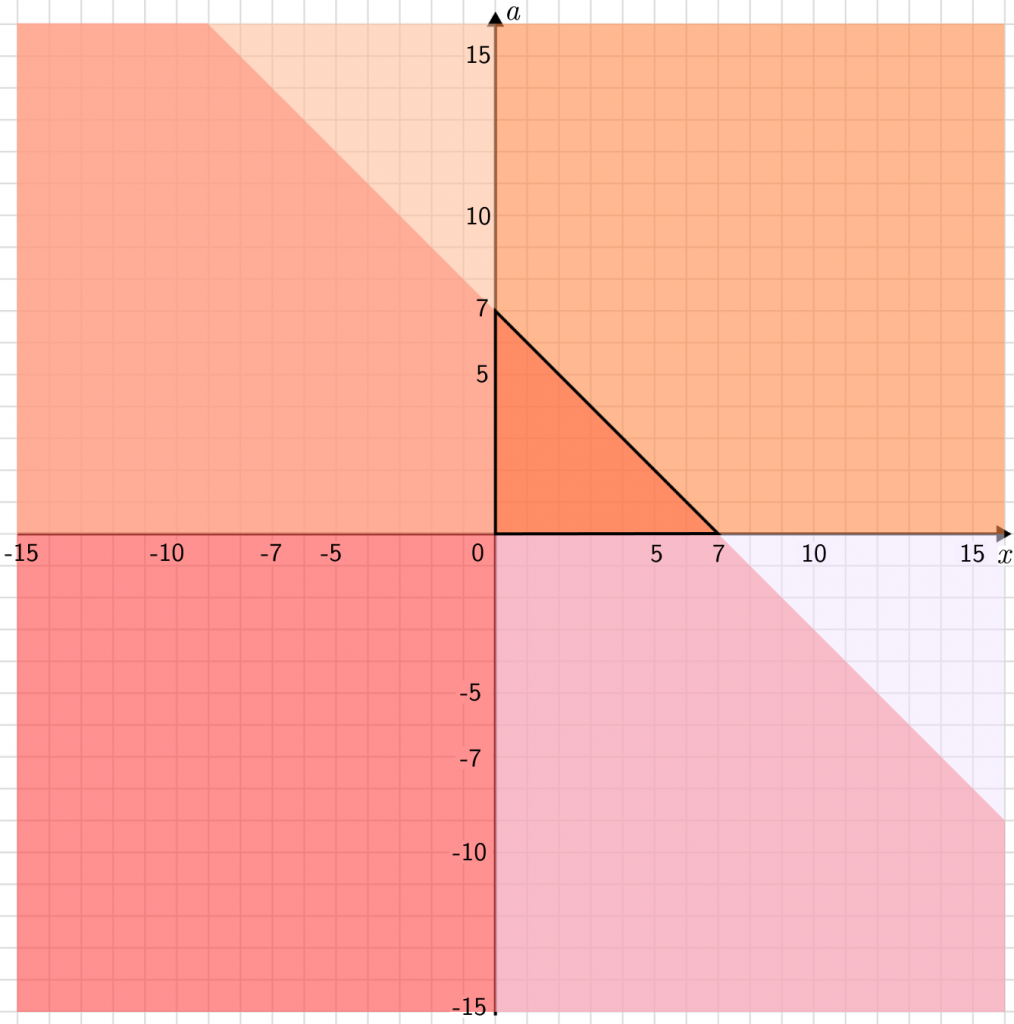
Треугольник, в котором они пересекаются, и будет задаваться условием
x\geqslant0;a\geqslant0 => x+a\leqslant7=>a\leqslant7-x
Мы как бы трижды отрезали все ненужное, и в результате из всей плоскости у нас остался лишь маленький треугольник.
Аналогичным способом получаем еще три треугольника.
x<0;a\geqslant0 => -x+a\leqslant7=>a\leqslant7+x
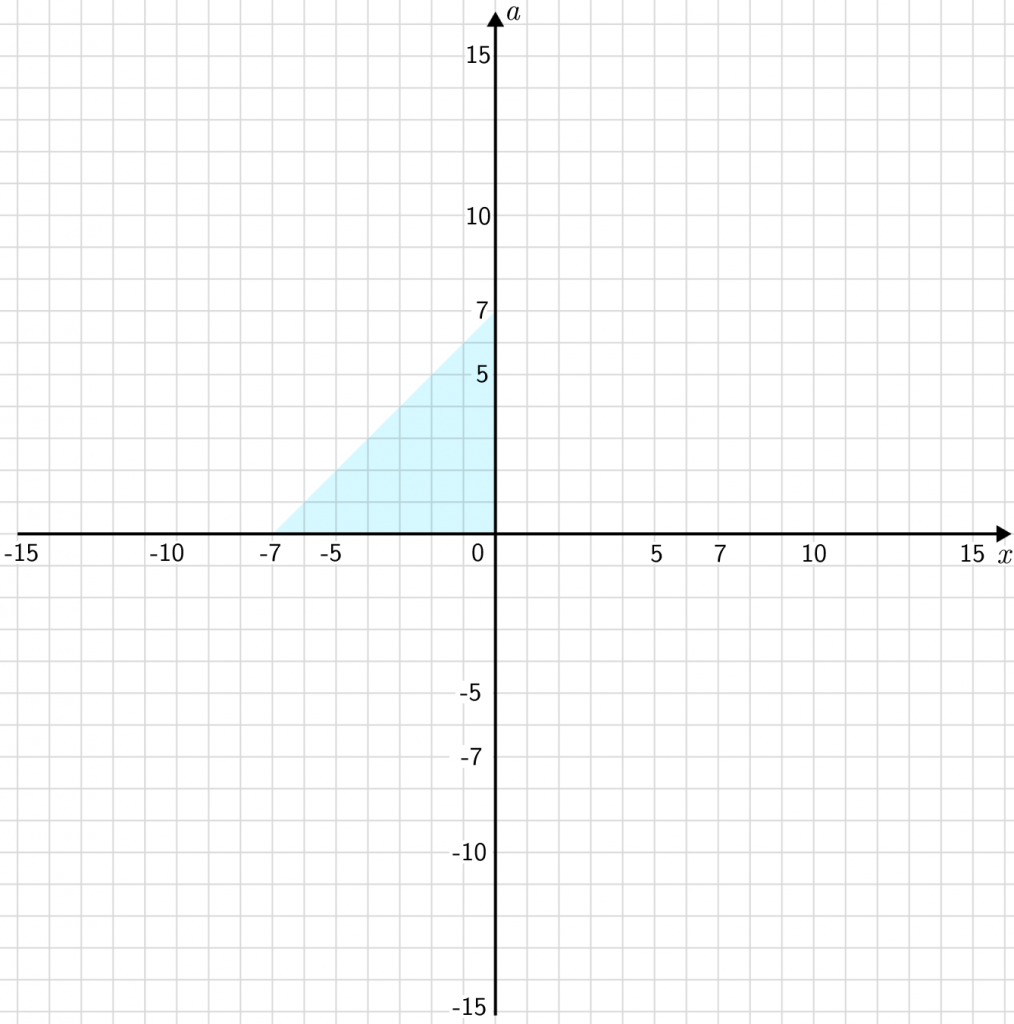
x<0;a<0 => -x-a\leqslant7=>a\geq-7-x
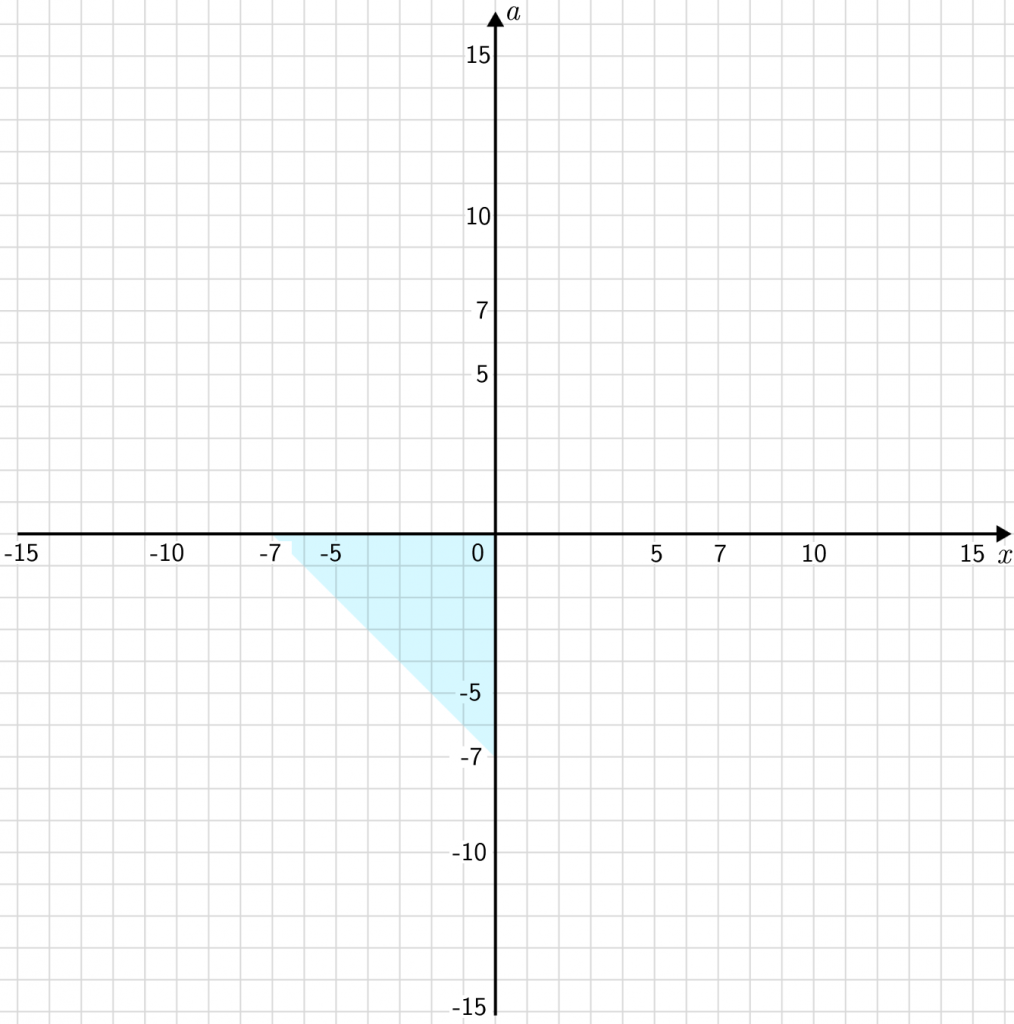
x\geq0;a<0 => x-a\leqslant7=>a\geq-7+x
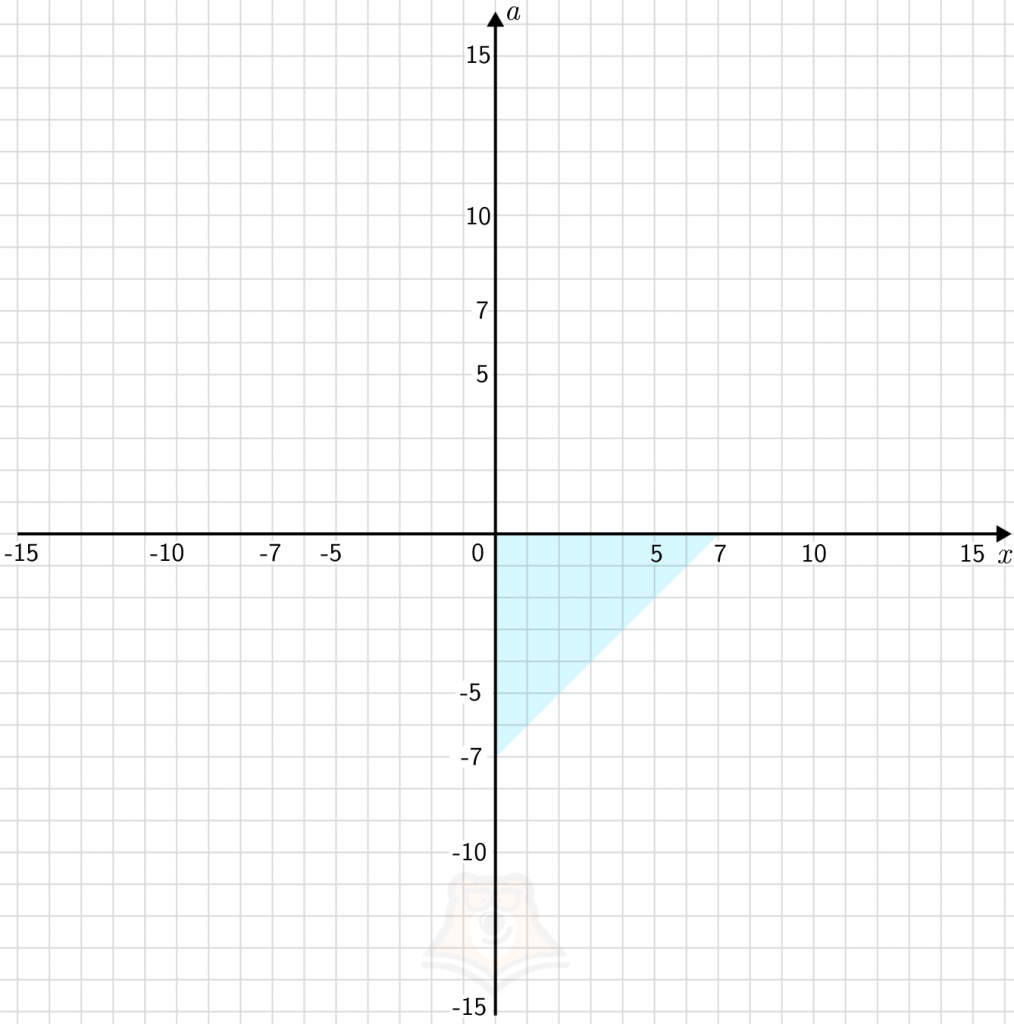
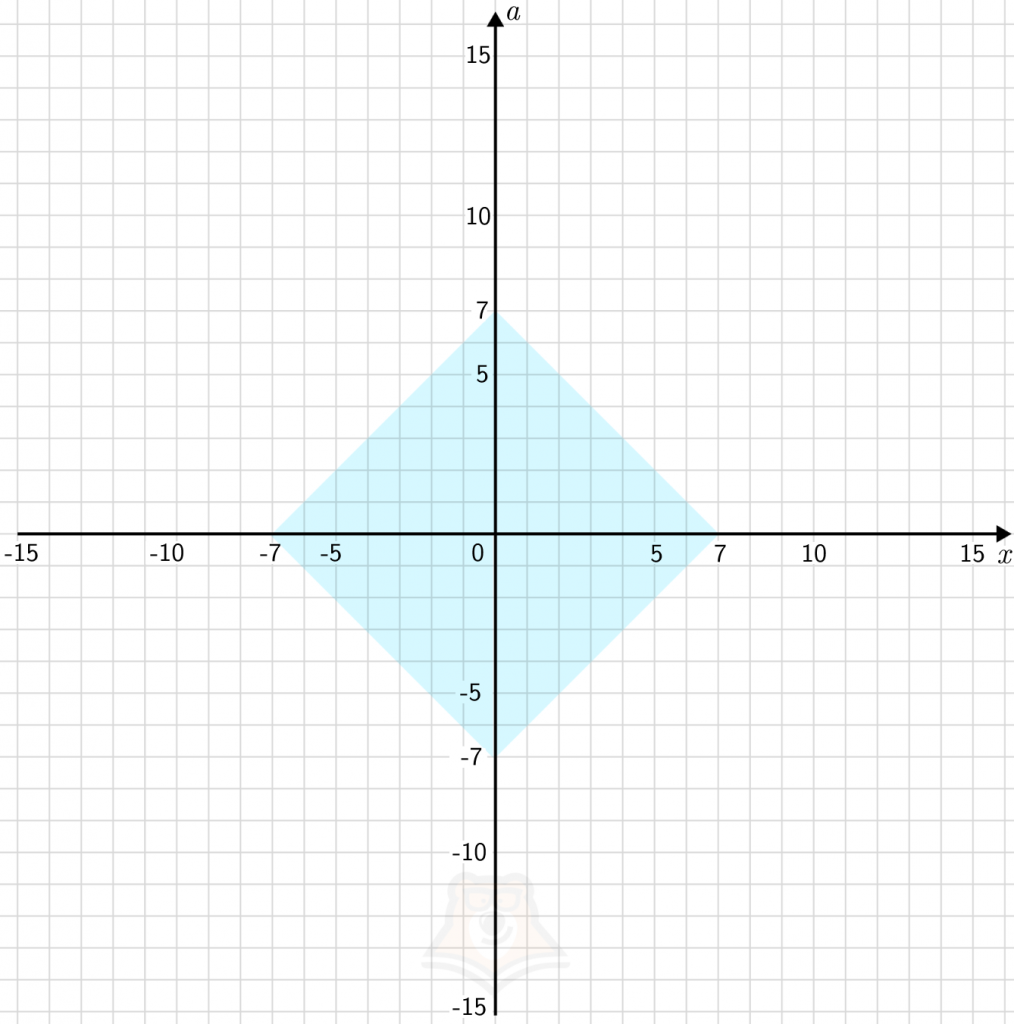
Объединив все графики, получим квадрат, ограниченный прямыми
a = x - 7, a = x + 7, a = - x - 7, a = - x + 7
Шаг 2. Рассмотрим второе неравенство системы и преобразуем его.
x^2 + 4x < 8a + 36
8a > x^24x - 36
a>\frac{1}{8}(x^2+4x-36)Это часть плоскости, ограниченная параболой
\frac{1}{8}(x^2+4x-36)Построим ее, вершина параболы будет лежать в точках:
x_{в}=-\frac{4}{2}=-2a_{в}=\frac{1}{8}((-2)^2+4(-2)-36)=\frac{1}{8}(4-8-36)=-5Поскольку знак неравенства строгий, то и сама парабола будет обозначаться пунктирной линией. То есть значения, лежащие на этой линии, не будут входить в нашу плоскость.
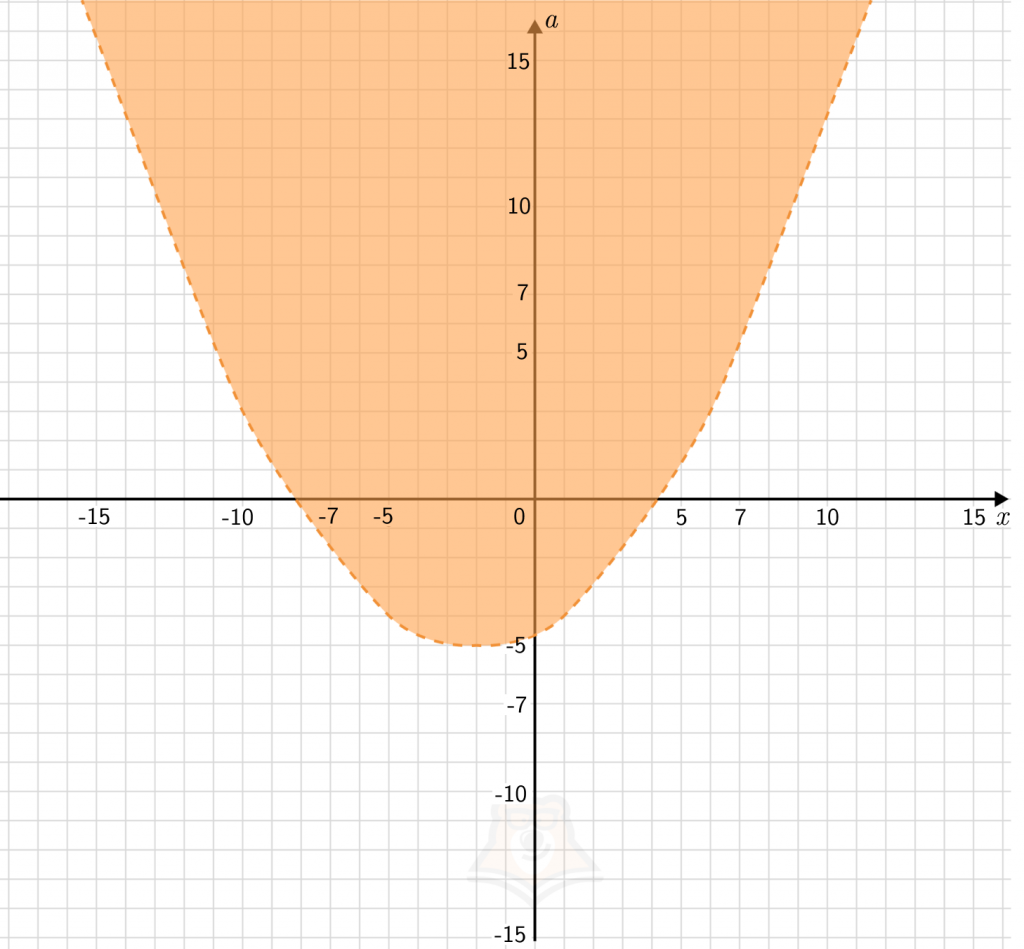
Шаг 3. Решением системы будет та часть плоскости, где парабола наложится на квадрат.
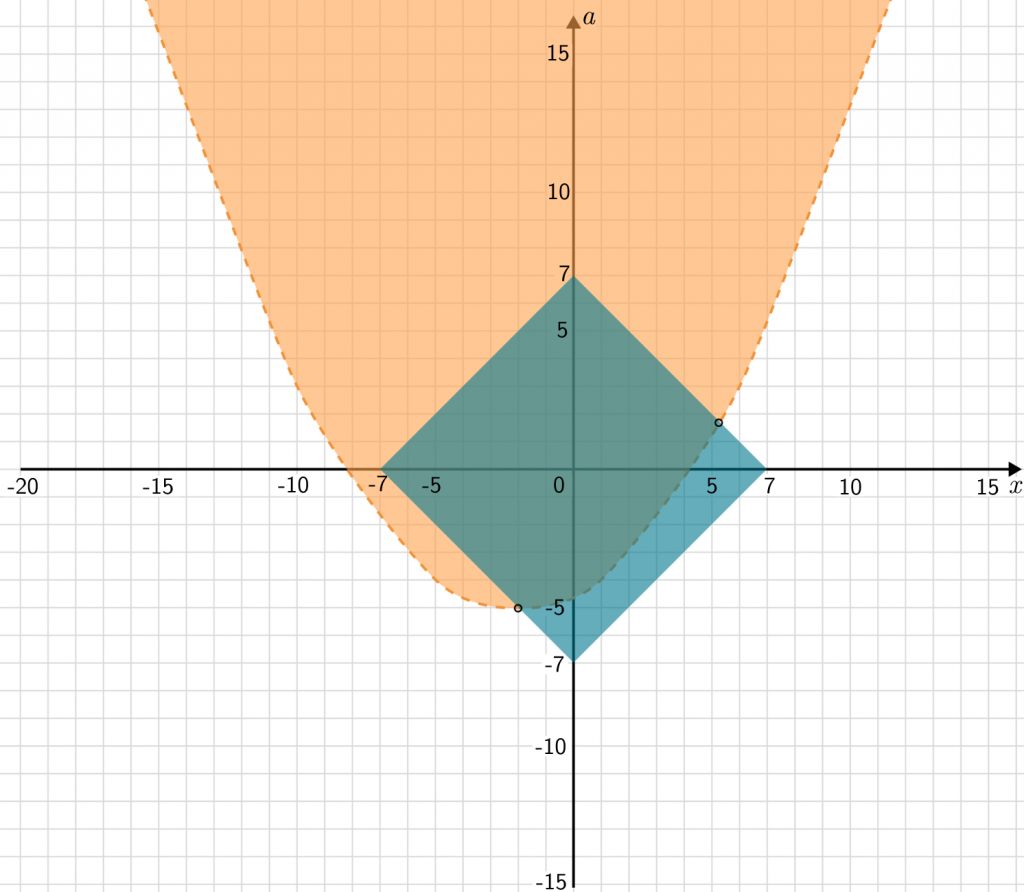
Шаг 4. По условию решения должны лежать в промежутке от -3 до 1. Построим еще одну плоскость.
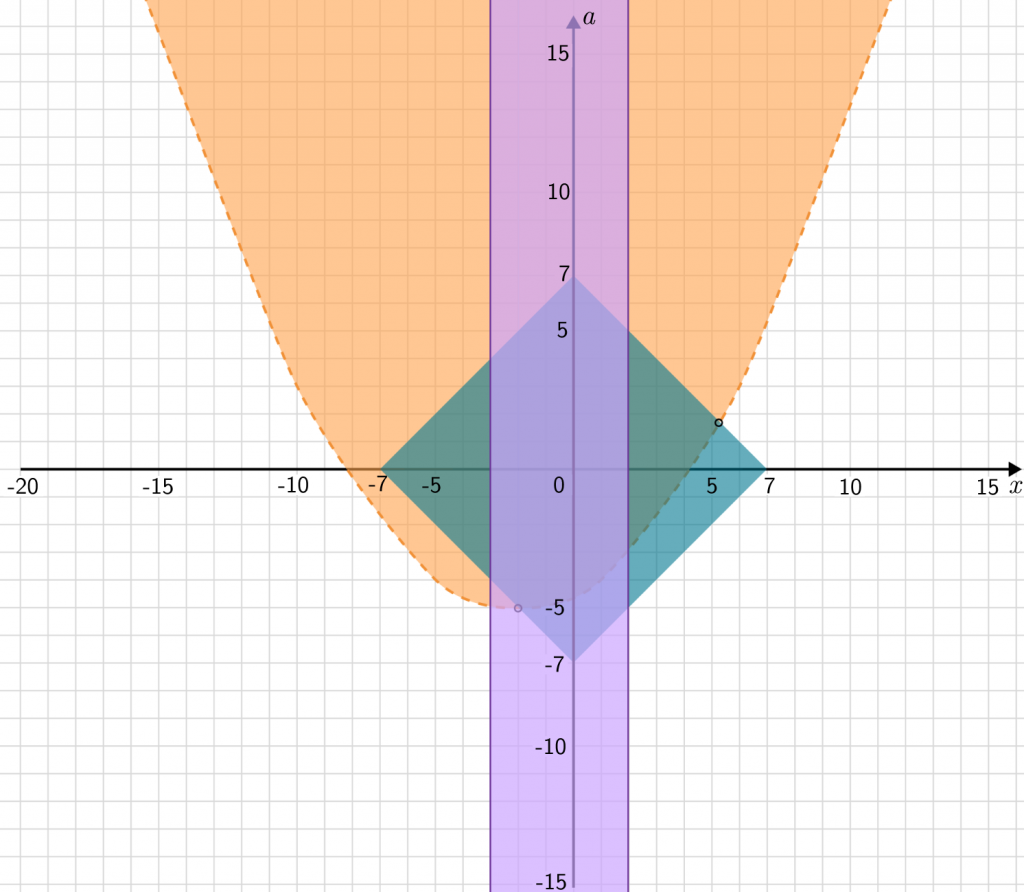
Нам нужно найти значения параметра а, которые лежат в промежутке пересечения всех трех плоскостей. Как их найти? Посмотреть значения по вертикальной оси, то есть по оси параметра.
Нам нужны наименьшее, наибольшее значения и все, что лежит между ними. То есть
A <a\leq B
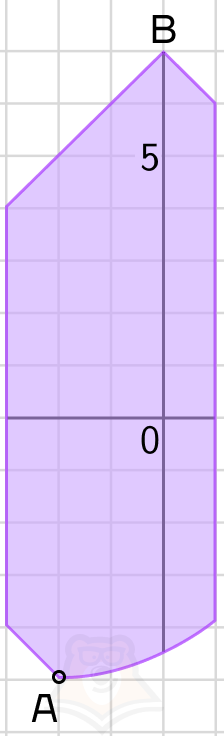
Шаг 5. Заметим, что точка А — точка пересечения прямой a = — x — 7 и параболы. Найдем точку их пересечения.
-x-7=\frac{1}{8}(x^2+4x-36)-8x-56=x2+4x-36
x^2+12x+20=0
D=144-4*1*20=144-80=64
x_{1}=\frac{-12+8}{2}=-2x_{2}=\frac{-12-8}{2}=-20Поскольку точка А лежит в промежутке [-3;1], то x2 не подходит. Прямая и парабола пересекаются в точке x = — 2.
Найдем, чему равно значение параметра в точке А.
a=-(-2)-7=2-7=-5
Шаг 6. Точка В — это вершина квадрата. А значит, точка В имеет координаты (0;7).
Шаг 7. Мы нашли значение параметра
-5< a\leq7
Это и будет ответ.
Ответ:
-5< a\leq7
Одним из вариантов 18 задания ЕГЭ по профильной математике с параметром являются задачи на единственность и количество решений. Звучит это очень страшно, но так ли это на самом деле? Давайте разбираться!
Задачи на единственность и количество решений
На ЕГЭ в заданиях с параметром часто встречаются задачи, где надо найти значения параметра при которых уравнение имеет определенное количество решений (одно, два, три и т.д.). Давайте разберемся, как же определить значения параметра, при котором уравнение имеет одно решение.
Обычно формулировка заданий примерно такая: «Найдите значение параметра (или параметров), при которых уравнение (или неравенство) имеет единственное решение».
Что же делать в такой ситуации? Давайте разбираться.
Для начала вспомним, что такое четная и нечетная функция.
Функция \(у = f (x)\) называется четной, если она не меняется, когда независимая переменная изменяет только знак, то есть, если \(f (-x) = f (x)\). Если же \(f (—x)= — f (x)\), то функция \(f (x)\) называется нечетной.
Разобравшись с четностью и нечетностью мы можем уже сделать какие-то выводы.
Если при решении задачи функция оказалась четной, то если \(x_1\) является решением уравнения, тогда и \(-x_1\) является решением уравнения. Следовательно, для единственности решения необходимо и достаточно, чтобы \(x_1=0\). Если функция окажется нечетной, то надо найти те значения параметра,при которых выполняется условие \(f(-x)=-f(x)\).
Тогда для решения будем придерживаться следующего алгоритма:
- находить возможные значения параметров из уравнения;
- для найденных значений параметров будем проверять, что других решений (кроме \(x=0\)) нет.
Среди задач на количество решений есть отдельный тип, где требуется найти все значения переменной, которые являются решением уравнения или системы при любом значении параметра. К таким задачам есть отдельный подход. Нужно попробовать найти такое значение параметра, чтобы наше уравнение превратилось в стандартное, а потом уже рассмотреть все остальные значения. Этот подход называется методом упрощающего значения. Звучит запутано, но все станет понятно, как только мы рассмотрим пример.
Рассмотрим еще один пример №18 из ЕГЭ по профильной математике.
Задание. Найдите все значения x, удовлетворяющие уравнению \(log_3(\sqrt{7-x}-|a|)=log_{3+|a|}(5-\sqrt{2-x})\) при любом значении параметра a.
Решение.
Шаг 1. Можем ли мы решить это уравнение каким-нибудь общим способом? Нет. В этом уравнении мы имеем логарифмы с разными основаниями, причем в одно из них входит параметр. Если попробовать перейти к другим основаниям, то все станет еще сложнее. Давайте попробуем понять, как здесь подобрать значение параметра так, чтобы мы получили простое уравнение.
Если \(a=0\), то наше уравнение станет обычным логарифмическим:
\(log_3\sqrt{7-x}=log_3(5-\sqrt{2-x})\)
Нам будет достаточно рассмотреть только этот случай, потому что если какое-то значение переменной является решением в случае \(a=0\), то нам надо проверить, будет ли оно являться решением при всех остальных значениях параметра, чтобы решить задачу. А если значение не является решением в случае \(a=0\), то оно сразу нам не подходит, поскольку в условии задачи нас просят найти все значения переменной, удовлетворяющие уравнению при любом значении параметра, то есть и при нуле.
Давайте решим полученное уравнение. У логарифмов одинаковые основания, поэтому должны быть равны аргументы. Для решения такого уравнения нам надо записать систему, чтобы учесть, что уравнения под логарифмом должны быть положительны, потому что такое требование накладывает ОДЗ логарифма. В нашем случае достаточного одного такого условия, поскольку уравнения равны между собой:
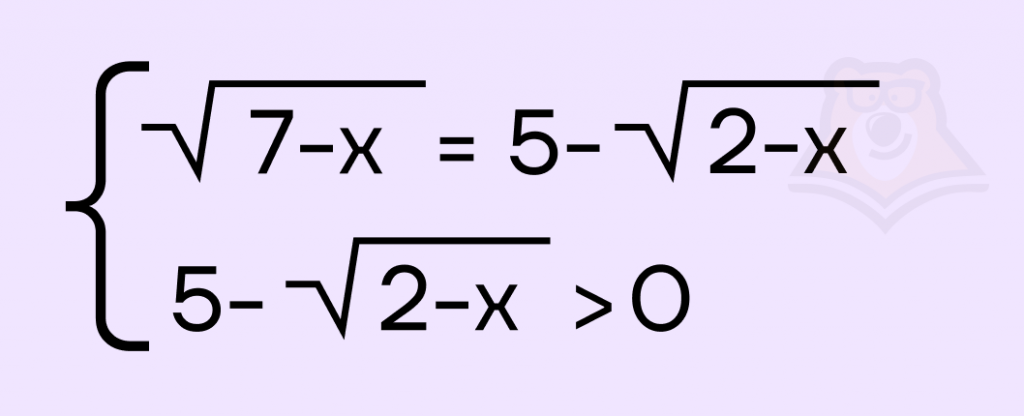
Шаг 2. Решаем каждое уравнение системы.
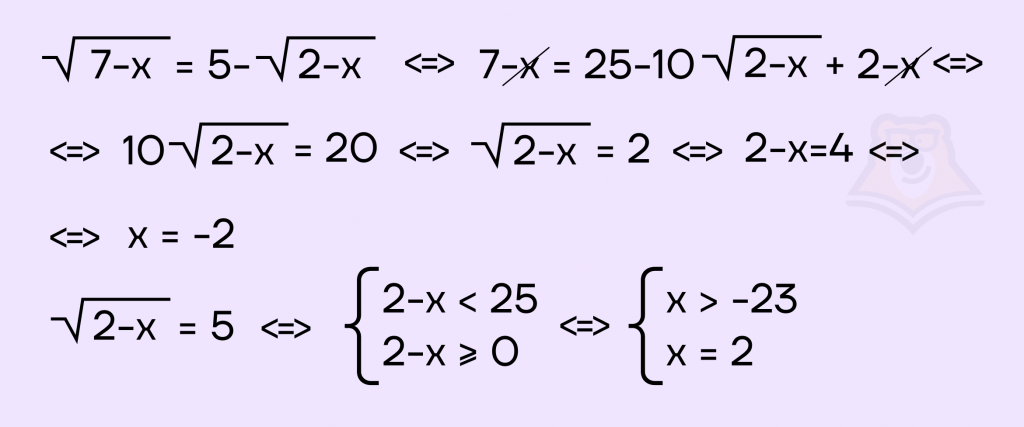
Шаг 3. Вернемся к системе и запишем ее решение.
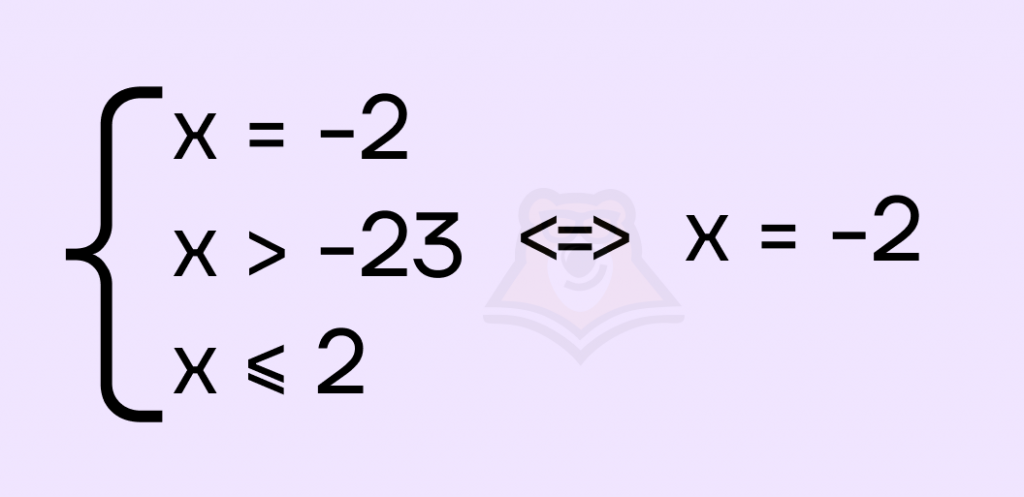
Шаг 4. Подставим наш корень в исходное уравнение, чтобы проверить, является ли он решением и при других значениях параметра.
\(log_3(2-|a|)=log_{3+|a|}3\)
Уравнение под логарифмом должно быть положительным, поэтому нам необходимо наложить условие на модуль параметра: \(2-|a|>0\). Значит, \(-2\) не будет корнем при любом значении параметра. Получается, значений x, которые являются решениями уравнения для любого значения параметра, нет.
Ответ: таких значений нет.
Мы можем расслабиться, выйти из образа аналитика, снять очки и отдохнуть. Главное, мы можем гордиться собой, ведь мы разобрали два новых принципа решения параметров.
Как можно сломать функцию? Где можно встретить идеальную симметрию? На эти и многие другие вопросы вы узнаете ответ в статье «Свойства функций в задачах с параметром».
Фактчек
- Аналитический способ решения параметров — использование алгебраических преобразований и рассуждений без привлечения графических интерпретаций.
- Для решения параметров аналитическим способом важно уметь преобразовывать уравнения, неравенства и их системы.
- При решении параметров аналитикой важно уметь анализировать функции, их поведение и свойства. Это позволит прийти к правильным выводам при решении и правильно найти значения параметра.
- Некоторые примеры с параметров выгоднее решать в плоскости хОа. В этой плоскости параметр будет либо зависимой, либо независимой переменной.
- Функции делятся на четные и нечетные. Это поможет анализировать функции для решения параметров
Проверь себя
Задание 1.
В каких случаях у совокупности есть решения?
- Если выполняется хотя бы одно из ее условий.
- Если выполняются все условия.
- В любом случае, даже если ни одно из условий не будет выполнено.
- Нет верного ответа.
Задание 2.
В каких случаях у системы есть решения?
- Если выполняется хотя бы одно из ее условий.
- Если выполняются все условия.
- В любом случае, даже если ни одно из условий не будет выполнено.
- Нет верного ответа.
Задание 3.
Дана система из совокупности и уравнения. Как ее можно преобразовать?
- Все элементы можно записать отдельно.
- Все элементы можно записать только в систему.
- Можно получить совокупность двух систем.
- Можно получить систему из двух совокупностей.
Задание 4.
Может ли параметр быть независимой переменной в функции?
- Не может.
- Может.
- Параметр не может быть переменной в функции, это просто число.
- Нет верных ответов.
Задание 5.
Какая часть плоскости задается неравенством \(x>0\)
- Все, что лежит выше оси х, включая саму ось.
- Все, что лежит выше оси х, исключая саму ось.
- Все, что лежит правее оси х, включая саму ось.
- Все, что лежит правее оси х, исключая саму ось.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 2 5. — 4


 к списку статей
к списку статей





