Элементы треугольника
На этой странице вы узнаете
- Фокус с пилой и ящиком: что может «распилить» сторону треугольника пополам?
- Слышите писк? Где-то бегает крыса! Что она делает?
- «Ортоцентр» — это что-то из медицины?
Может ли упасть треугольник? Если пофантазировать, что он стоит на одном из углов — вполне возможно. А может ли упасть высота треугольника и куда? Ответ на этот вопрос мы спрятали в статье.
Медиана
Нельзя рассматривать тему треугольников и не затронуть такие понятия, как медиана, биссектриса, высота и средняя линия. Большая часть свойств треугольников связаны с этими элементами.
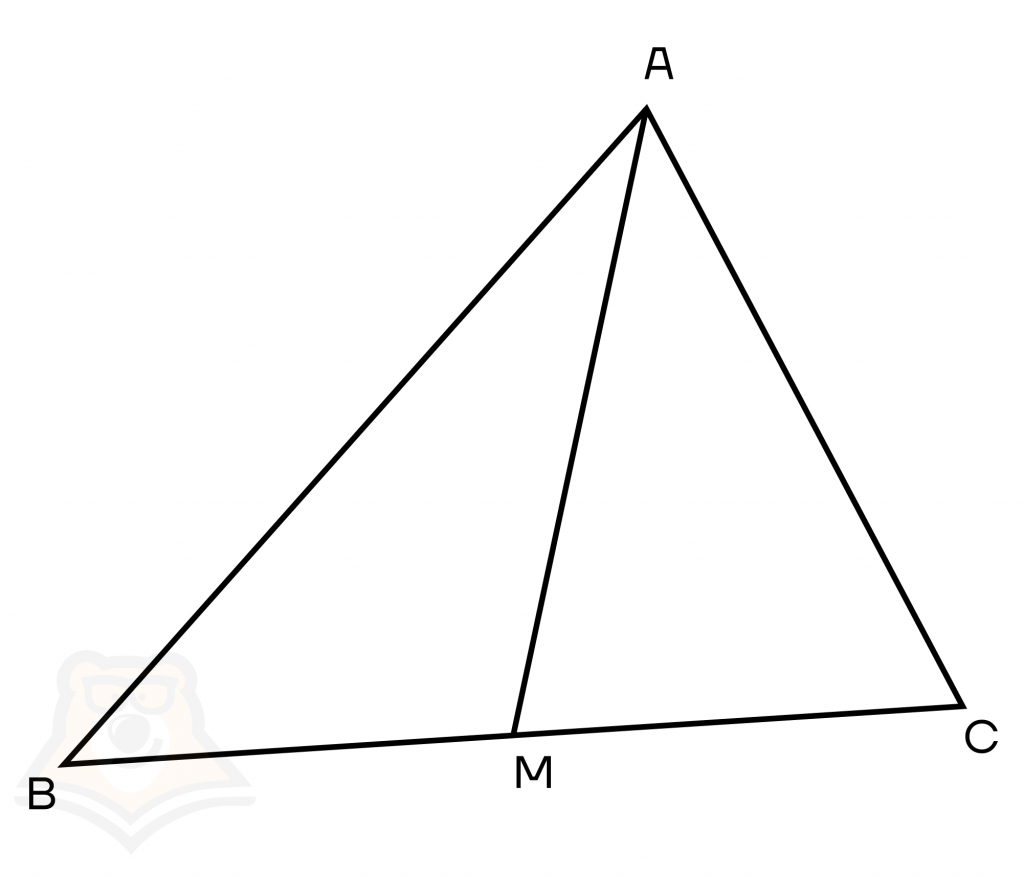
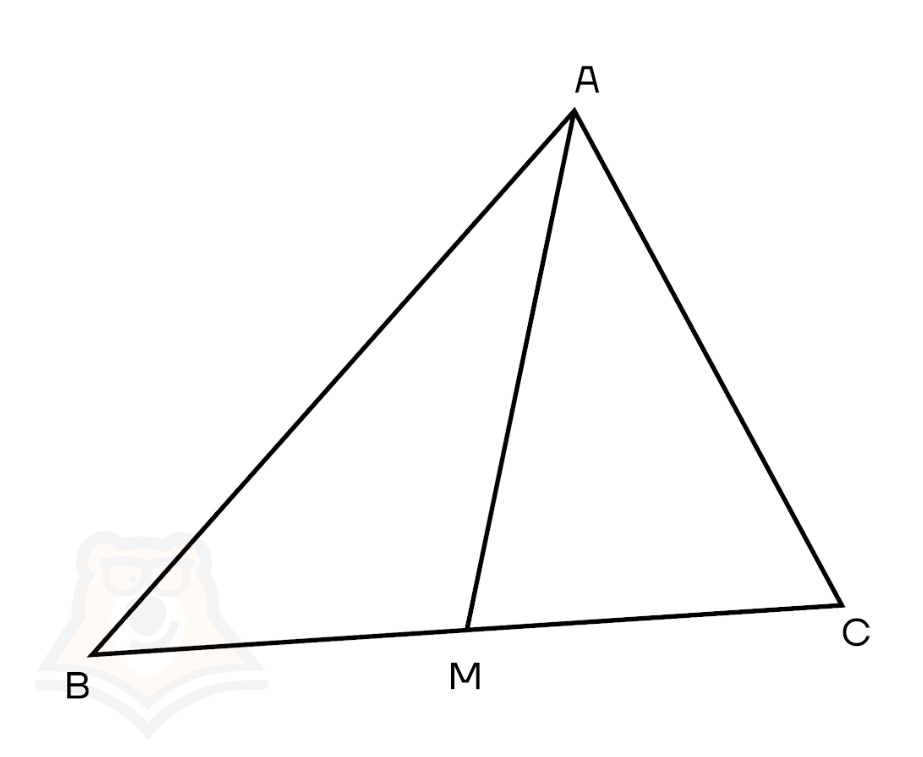
Медиана — это отрезок, который соединяет вершину треугольника с серединой противоположной стороны.
На рисунке медианой будет отрезок АМ.
| Фокус с пилой и ящиком: что может «распилить» сторону треугольника пополам? Математики иногда любят пошалить. И фокусы тоже любят. Например, знаменитый трюк с распиливанием человека можно повторить на треугольнике. Для этого даже есть специальная пила — медиана. |

Медиана обладает важными свойствами, которые могут пригодиться для решения задач.
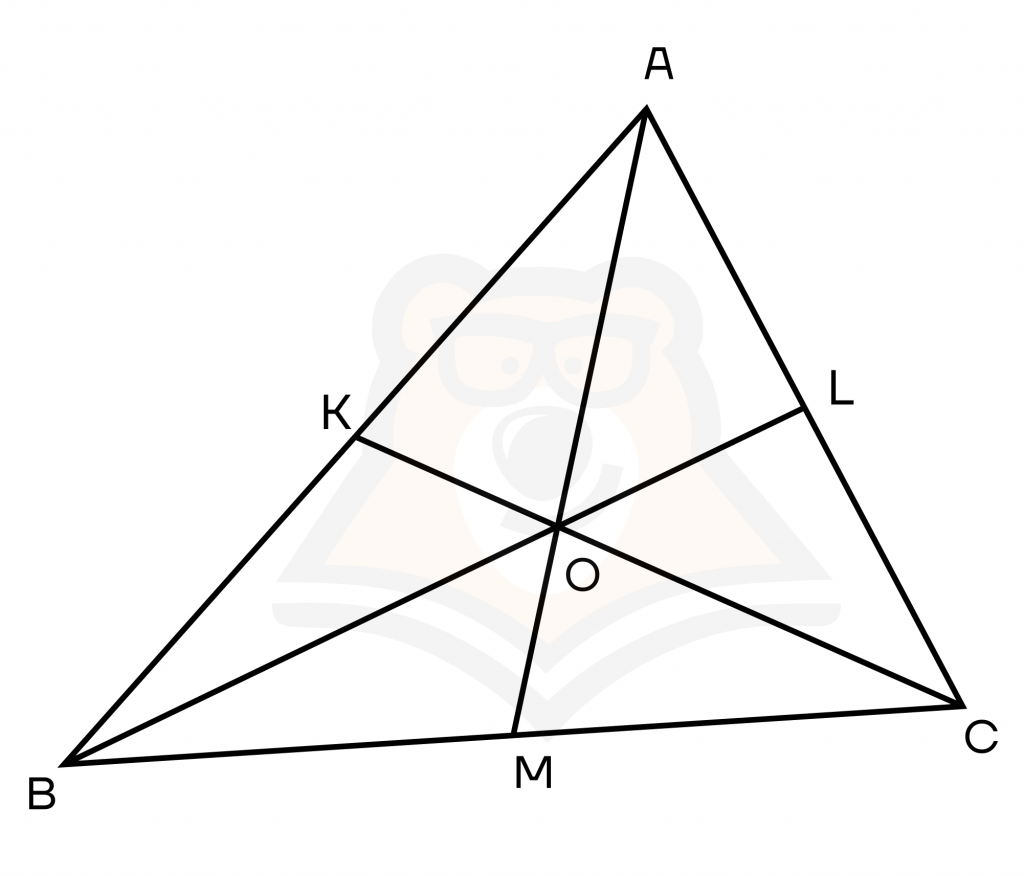
Свойство 1. Если в треугольнике провести три медианы, то они пересекутся в одной точке. На рисунке это точка О (рисунок к свойству 2).
Свойство 2. Точкой пересечения медианы делятся в отношении 2:1, считая от вершины.
Следовательно, выполняется равенство AO : OM = BO : OL = CO : OK = 2 : 1.
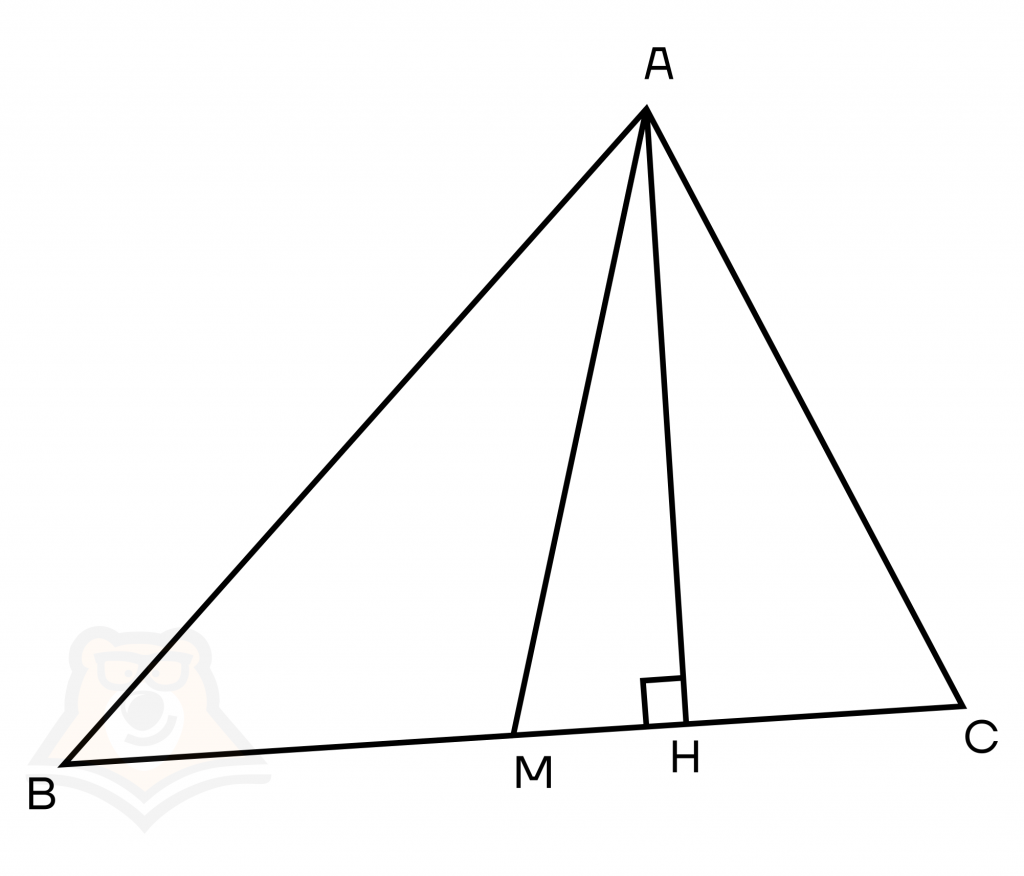
Свойство 3. Медиана делит треугольник на два равных по площади треугольника.
Докажем это. Проведем медиану АМ и высоту АН. Поскольку медиана делит сторону пополам, то ВМ = МС.
Забегая вперед, скажем, что площадь треугольника равняется \(\frac{1}{2}ah\), где а — основание, h — высота, проведенная к основанию. Найдем площади треугольников ВАМ и МАС:
\(S_{BAM} = \frac{1}{2} * BM * AH\)
\(S_{MAC} = \frac{1}{2} * MC * AH\)
Поскольку ВМ = МС, то SBAM = SMAC.
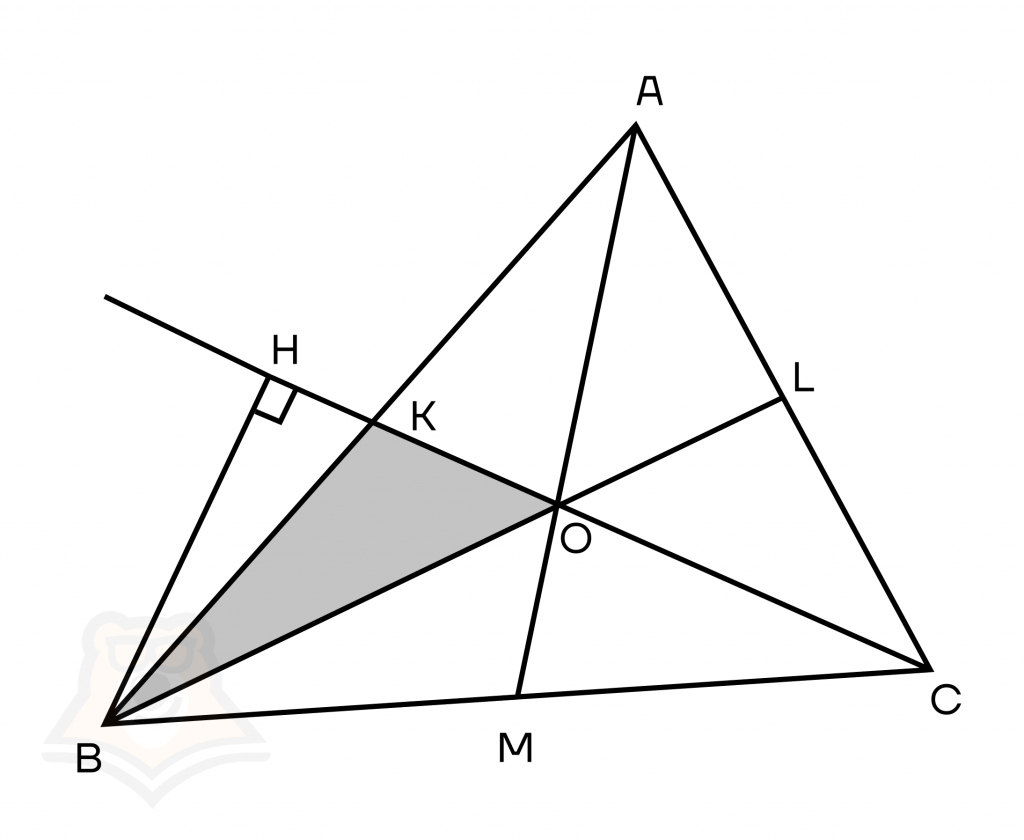
Свойство 4. Если в треугольнике проведены все три медианы, то они делят треугольник на шесть равновеликих треугольников.
Равновеликие треугольники — это треугольники, площадь которых равна.
Докажем это. Найдем площадь \(S_{BOK} = \frac{1}{2} * OK * BH\). Вспомним, что медианы точкой пересечения делятся в отношении 2:1, следовательно, СО:ОК = 2:1, откуда получаем, что \(OK = \frac{CK}{3}\).
Подставим полученное значение в формулу площади: \(S_{BOK} = \frac{1}{2} * \frac{1}{3} * CK * BH
Рассмотрим площадь треугольника ВКС: \(S_{BKC} = \frac{1}{2} * KC * BH\). Следовательно, мы можем представить площадь треугольника ВОК как \(S_{BOK} = \frac{1}{3}S_{BKC}\).
Теперь нужно вспомнить предыдущее свойство, что медиана разбивает треугольник на два равновеликих треугольника, следовательно, \(S_{BKC} = \frac{S_{BAC}}{2}\). Тогда \(S_{BOK} = \frac{S_{BKC}}{6}\).
Аналогично можно найти площадь остальных пяти треугольников.
Чтобы найти длину медианы, можно воспользоваться следующей формулой.
\(m_c = \frac{\sqrt{2a^2 + 2b^2 — c^2}}{2}\)
Очень важно следить за тем, как подставлять длины сторон в формулу. Запись mc означает, что медиана проведена к стороне треугольника с.
Найдем по формуле длину медианы АМ:
\(AM = \frac{\sqrt{2AB^2+ 2AC^2 — BC^2}}{2}\)
Биссектриса треугольника
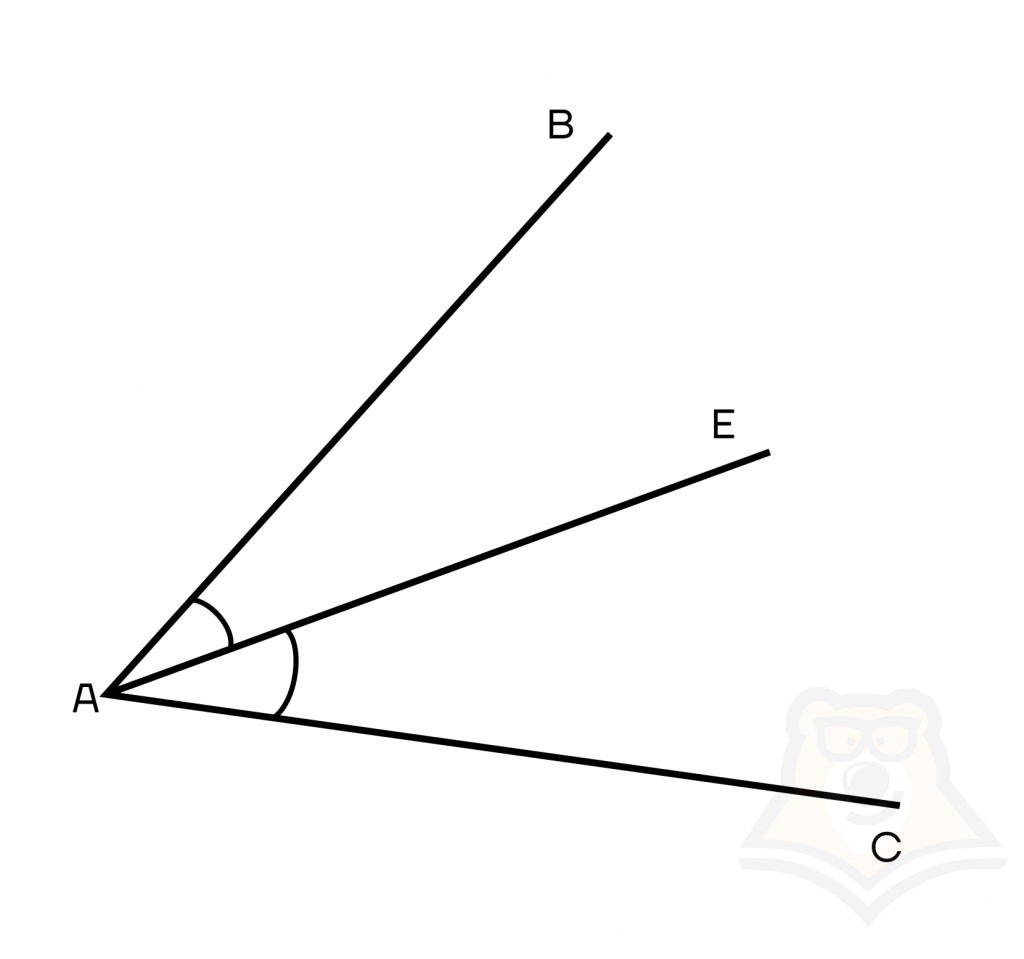
Биссектриса угла — это луч, который делит угол пополам.
На рисунке проведена биссектриса угла АЕ, тогда ∠BAE = ∠CAE.
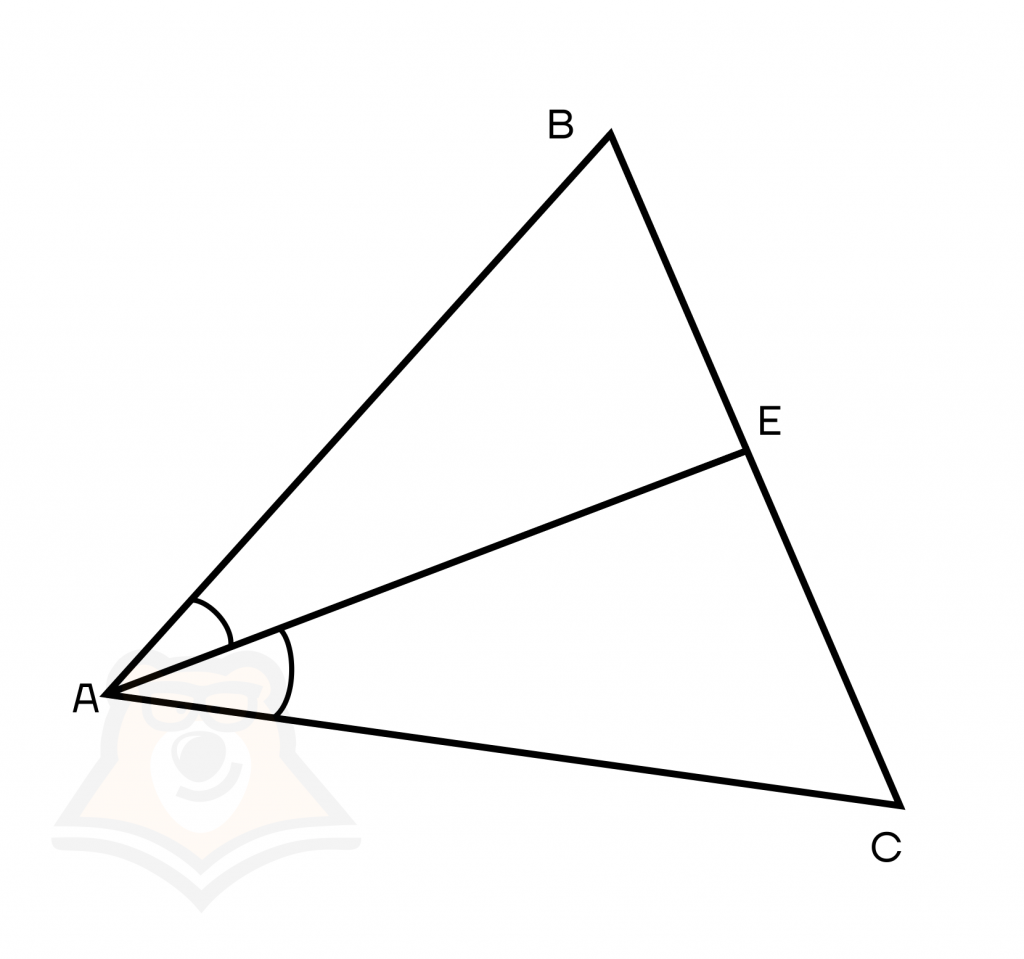
Биссектриса треугольника — это отрезок, который соединяет вершину треугольника с точкой на противолежащей стороне и который делит угол треугольника пополам.
| Слышите писк? Где-то бегает крыса! Что она делает? «Биссектриса — это крыса, которая бегает по углам и делит угол пополам». Этот забавный стишок поможет запомнить свойство биссектрисы. |

На рисунке АЕ — биссектриса.
Рассмотрим свойства биссектрисы.
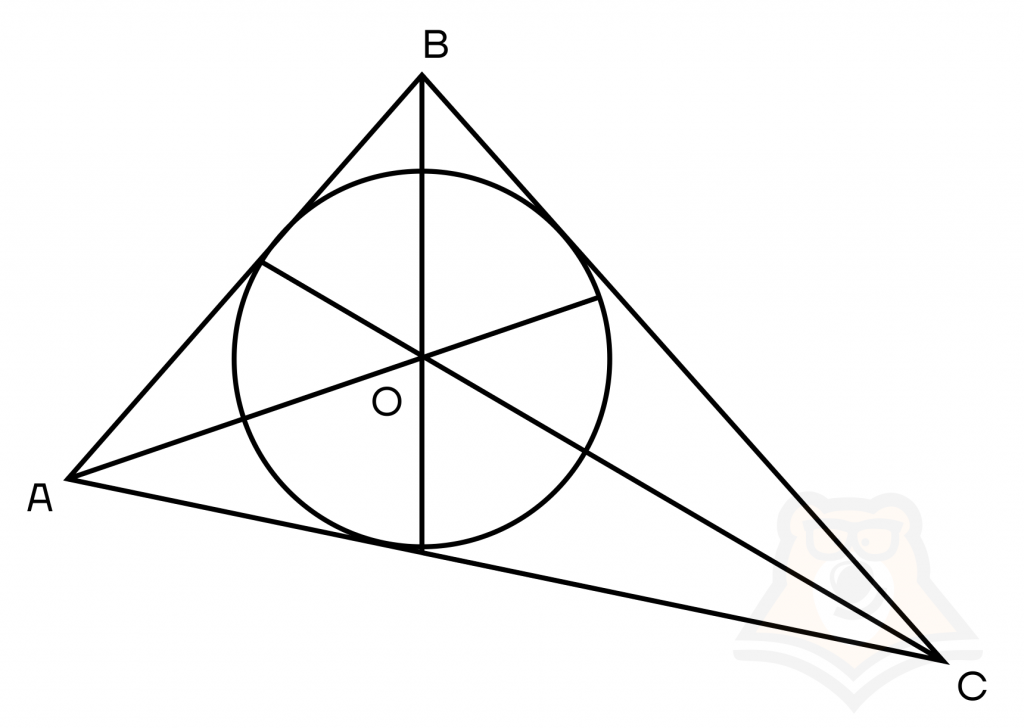
Свойство 1. Если в треугольнике провести три биссектрисы, то они пересекутся в одной точке. На рисунке это точка О (рисунок к свойству 2).
Свойство 2. Точка пересечения биссектрис треугольника — это центр вписанной в треугольник окружности.
Свойство 3. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
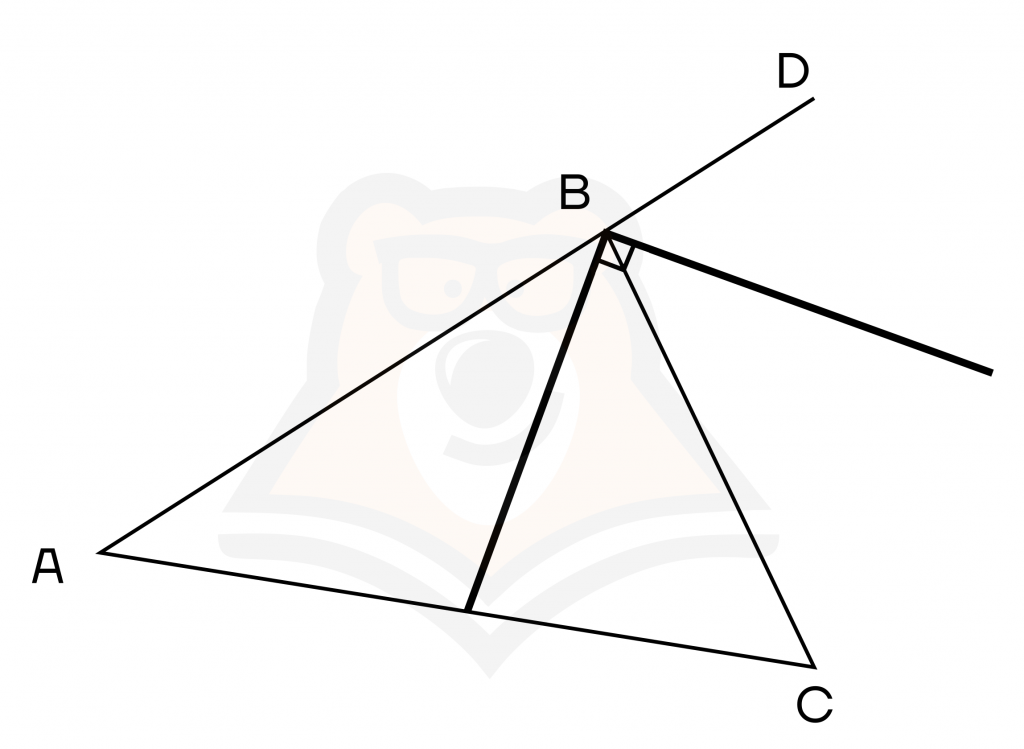
Вспомним, что сумма смежных углов равна 180° . Пусть угол АВС равен 2x, а угол CBD равен 2y. Биссектрисы делят их на два угла величиной х и у.
Тогда угол, образованный биссектрисами, будет равен х + у. Найдем, чему будет равняться это выражение.
2х + 2у = 180°
2(х + у) = 180°
х + у = 90°
Следовательно, утверждение выполняется.
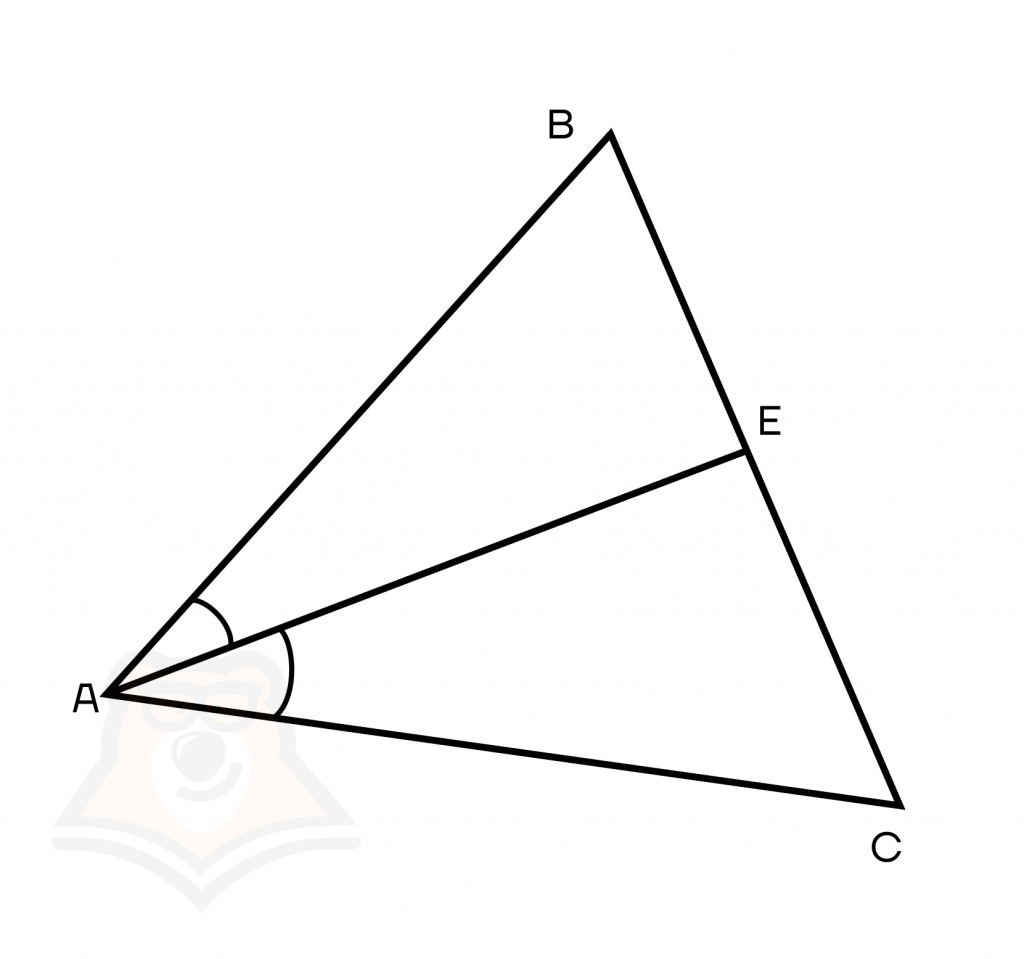
4 свойство. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.
Пусть АЕ — биссектриса, тогда можно составить уравнение \(\frac{BE}{EC} = \frac{AB}{AC}\).
Высота треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины на сторону треугольника.
Перпендикуляры встречаются очень часто в нашей жизни. Достаточно посмотреть на пол и стены в комнате: они будут перпендикулярны друг другу.
А чтобы было чуть легче запомнить, что такое высота, представь, что в чуме достроили вертикальную стену. Тогда эта стена будет перпендикулярна земле.

Пусть АН — высота, тогда ∠АНВ = ∠АНС = 90°.
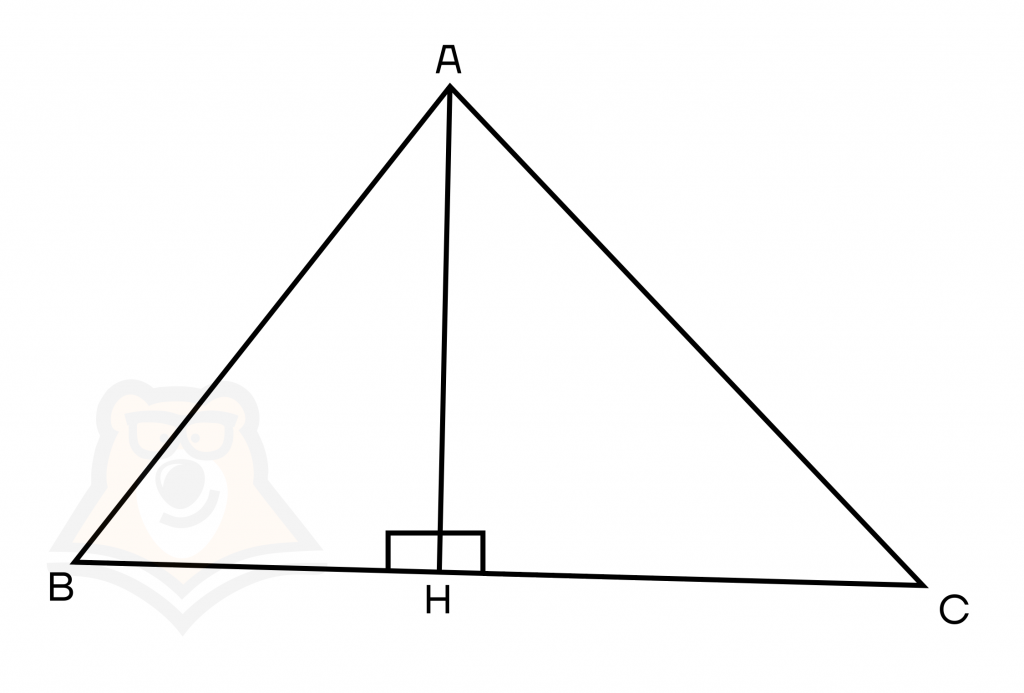
Перпендикуляры не всегда могут упасть на сторону треугольника, бывает, что высота падает на продолжение стороны. Поэтому важно знать, куда падает высота в разных треугольниках.
- В остроугольном треугольнике все высоты будут падать на стороны треугольника. То есть все высоты будут лежать «внутри» треугольника.
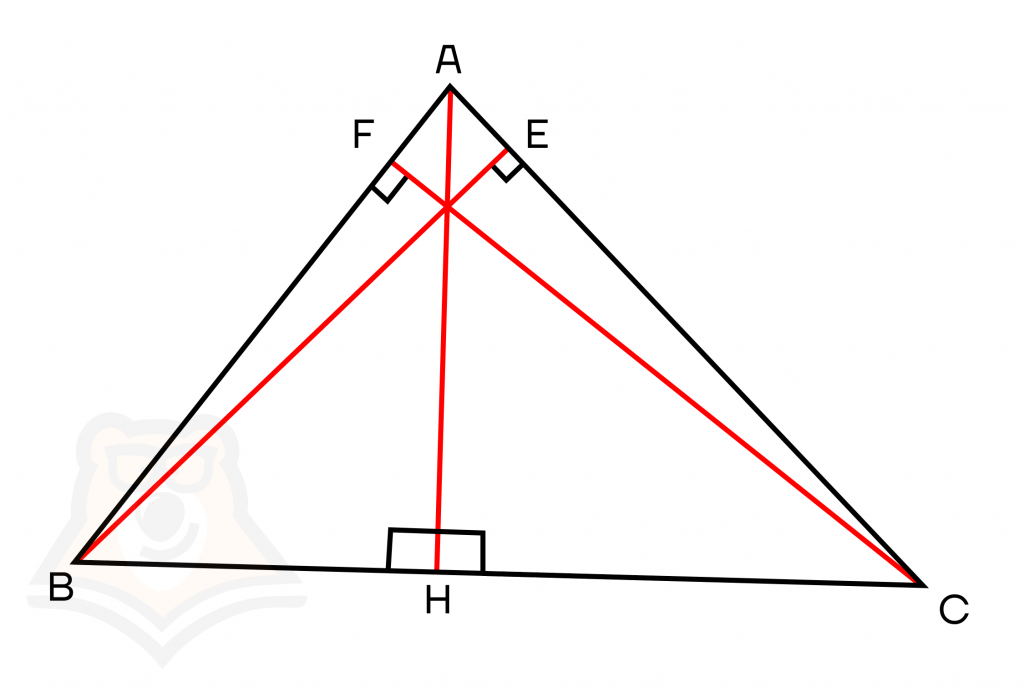
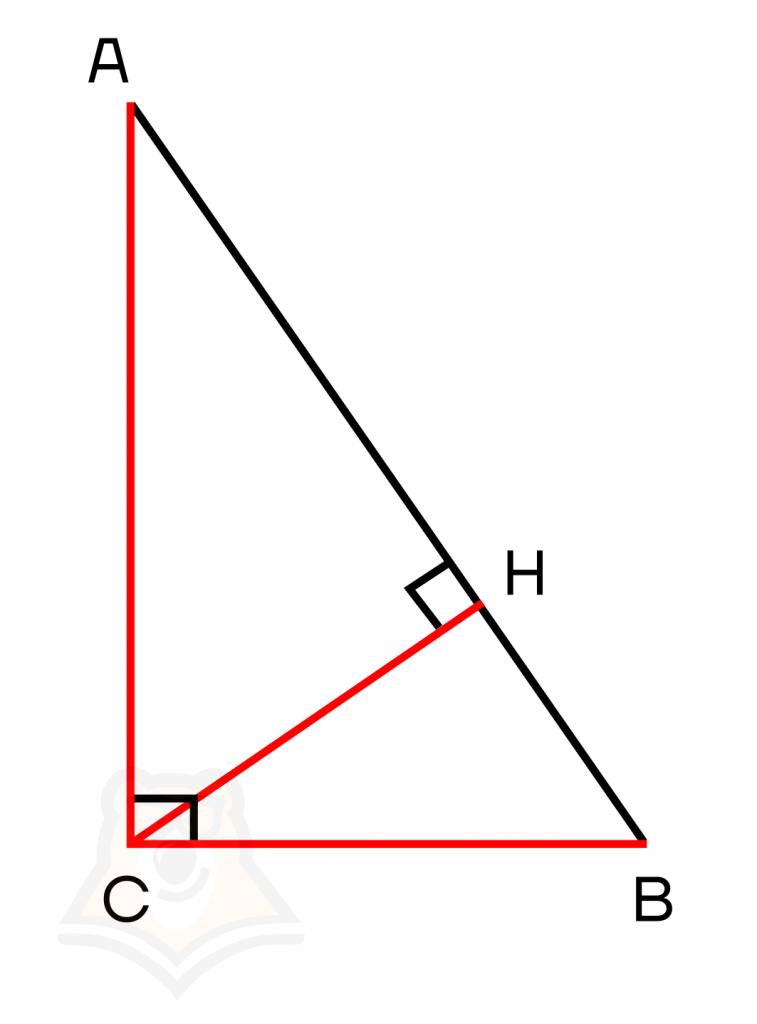
- В прямоугольном треугольнике две высоты будут совпадать со сторонами (и тем самым образуют прямой угол). Третья высота будет лежать «внутри» треугольника.
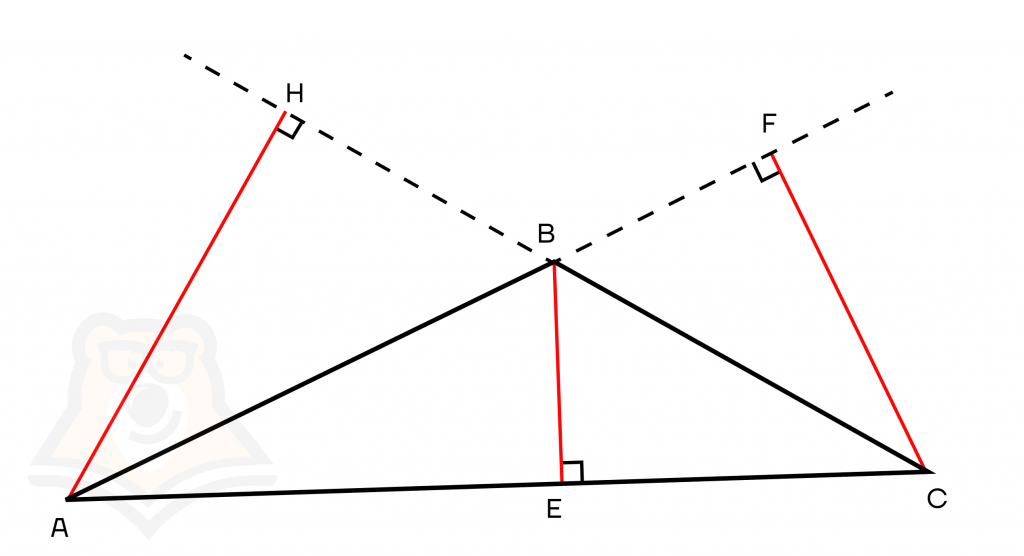
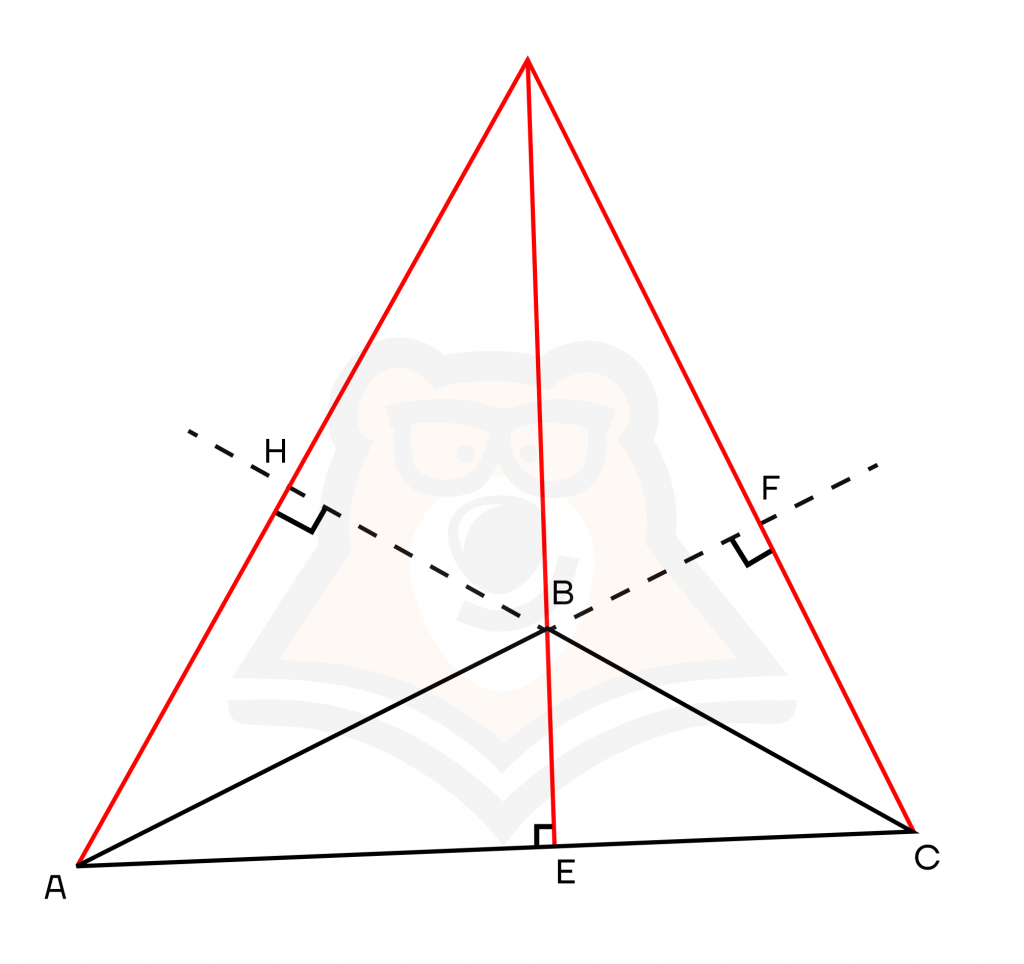
- В тупоугольном треугольнике две высоты (проведенные из вершин острых углов) будут лежать за пределами треугольника, а высота, проведенная из тупого угла, будет лежать «внутри» треугольника.
| «Ортоцентр» — это что-то из медицины? Мы часто слышим такие специальности врачей как ортопед и ортодонт, иногда даже посещаем их. Может показаться, что ортоцентр — это какой-то особенный медицинский центр. На самом деле, приставка орто- означает «правильный» или «прямой». У треугольника есть «правильный» центр (точка), где пересекаются высоты треугольника. Такая точка и будет называться ортоцентром треугольника. Важно помнить, что: — В остроугольном треугольнике ортоцентр будет лежать «внутри» треугольника. — В прямоугольном треугольнике ортоцентр будет совпадать с вершиной прямого угла треугольника. — В тупоугольном треугольнике ортоцентр будет лежать «снаружи» треугольника. |
Средняя линия треугольника
В теме треугольник нельзя не упомянуть про среднюю линию треугольника.
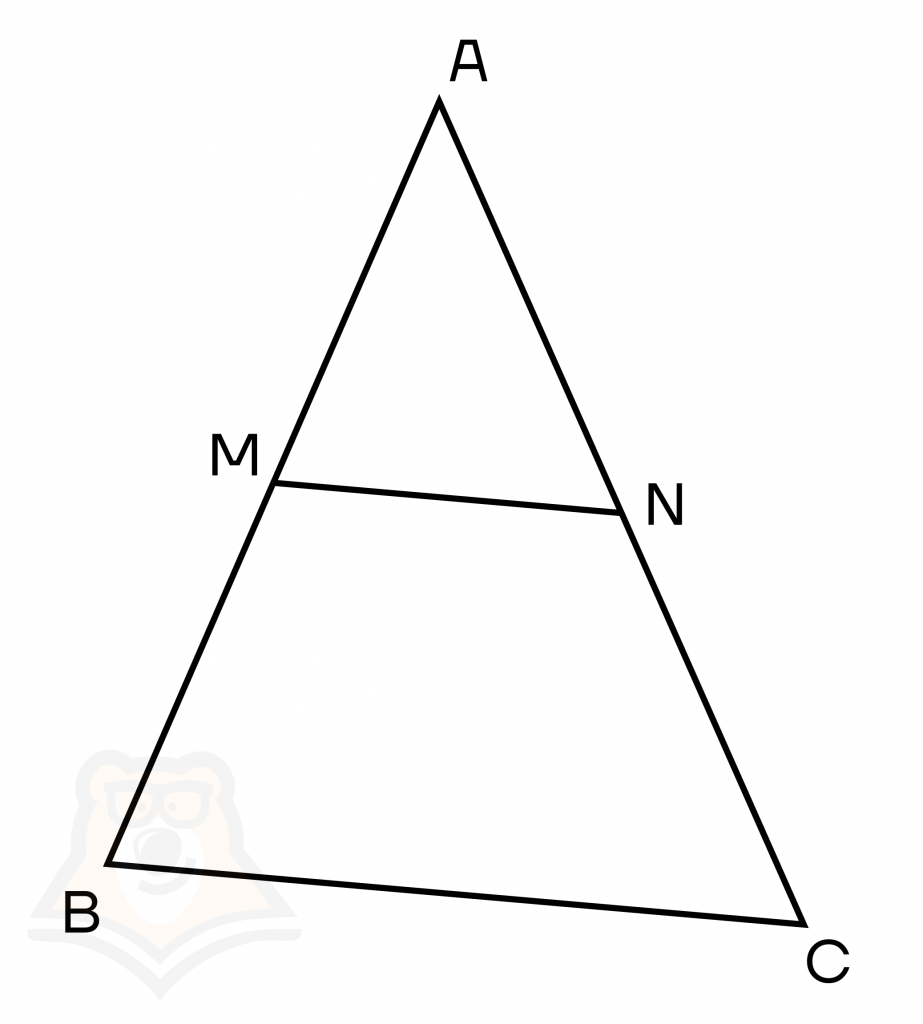
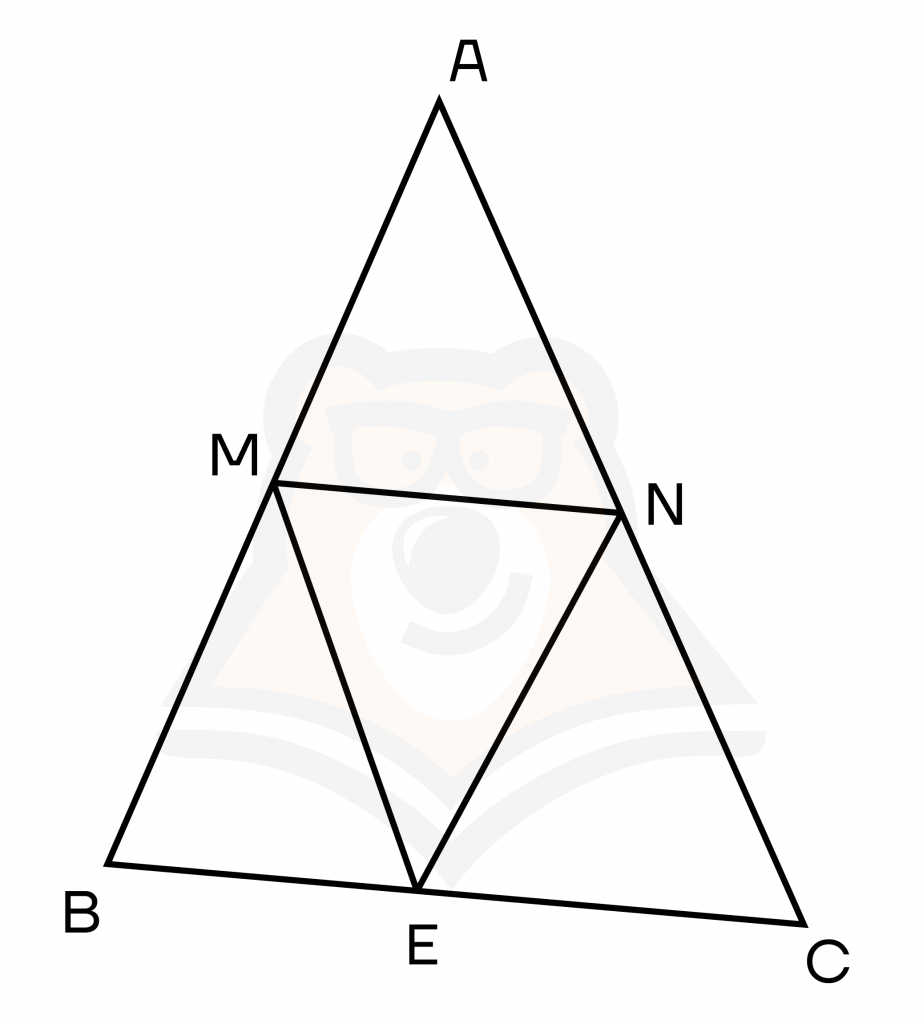
Средняя линия — это отрезок, соединяющий середины двух сторон.
Пусть M, N — середины сторон АВ и АС, тогда MN — средняя линия.
Средняя линия обладает важными свойствами.
1 свойство. Средняя линия параллельна стороне, которую она не пересекает и равна ее половине.
2 свойство. Средняя линия образует подобный треугольник, который в два раза меньше исходного. Получаем, что ABC ~ AMN.
Доказать подобие можно по двум углам: угол А — общий, углы В и М, а также С и N равны как соответственные углы при параллельных прямых (см. предыдущий рисунок).
3 свойство. Если провести в треугольнике три средних линии, то они образуют 4 равных треугольника, которые подобны исходному и в два раза меньше его.
Тогда получаем, что △AMN = △BME = △EMN = △ENC, при этом △ABC ~ △AMN.
Четыре замечательные точки треугольника
Для треугольника существует понятие «замечательной точки». Такими точками называют те, в которых пересекаются элементы треугольника. Всего их четыре:
- точка пересечения медиан;
- точка пересечения биссектрис;
- точка пересечения высот;
- точка пересечения серединных перпендикуляров.
Три из них мы уже рассмотрели, осталась лишь точка пересечения серединных перпендикуляров.
Серединный перпендикуляр – это прямая, перпендикулярная стороне треугольника и проходящая через ее середину.
Серединные перпендикуляры, а также точка, образованная их пересечением, очень тесно связаны с окружностью. Подробнее про них можно узнать в статье «Вписанная и описанная окружности».
Фактчек
- Медиана треугольника — это отрезок, который соединяет вершину треугольника и середину противоположной стороны. Все медианы треугольника пересекаются в одной точке и делятся ей в отношении 2:1, считая от вершины.
- Биссектриса треугольника — это отрезок, который соединяет вершину треугольника с точкой на противоположной стороне и делит угол треугольника пополам. Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
- Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его сторону. Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Средняя линия треугольника — это отрезок, соединяющий середины двух сторон. Средняя линия параллельна третьей стороне и равна ее половине.
Проверь себя
Задание 1.
В треугольнике начертили три медианы. Длина отрезка одной из них от вершины до точки пересечения медиан равняется 8. Чему равна эта медиана?
- 4
- 8
- 12
- 16
Задание 2.
Проведены биссектрисы внутреннего и внешнего углов треугольника. Биссектриса внутреннего угла делит его на два угла по 30 градусов. Чему равен внешний угол треугольника?
- 90°
- 60°
- 120°
- 180°
Задание 3.
Где будет лежать ортоцентр тупоугольного треугольника?
- «Внутри» треугольника.
- «Снаружи» треугольника.
- Ортоцентр будет совпадать с одной из вершин.
- В тупоугольном треугольнике нет ортоцентра.
Задание 4.
Средняя линия делит стороны треугольника a и b пополам и равняется 15. Чему равна сторона c?
- 15
- 30
- 7,5
- 225
Задание 5.
Средняя линия отсекает треугольник, площадь которого равна 6. Чему равна площадь всего треугольника, в котором проведена средняя линия?
- 24
- 12
- 6
- 3
Ответы: 1. — 3; 2. — 3; 3. — 2; 4. — 2; 5. — 1.


 к списку статей
к списку статей





