Тела вращения

На этой странице вы узнаете

• Как с помощью прямоугольника и скульптурного станка создать цилиндр?
• Причем тут тор и почему он без Локи?

Математика такая интересная наука, что голова идет кругом. А если я скажу, что в этом случае голова образует новую фигуру? Как это возможно — узнаем в статье.

Тела вращения

Мы прекрасно знаем, что такое вращение. Балерина, офисный стул, барабан стиральной машинки, планета Земля вращаются вокруг своей оси, как и много-много других примеров. 

Проведем эксперимент. 

Как с помощью прямоугольника и скульптурного станка создать цилиндр? Вырежем из бумаги прямоугольник и зафиксируем его на скульптурном станке. Скульптурный станок встречался нам во многих фильмах: обычно на нем лепят посуду и другие предметы из глины. Но главное, что нам нужно в станке, это его вращающаяся столешница. Раскрутим наш прямоугольник с очень-очень высокой скоростью.  Теперь прямоугольник будет казаться не плоской бумагой, а объемным цилиндром, в основании которого лежит  круг с радиусом, равным длине этого прямоугольника.

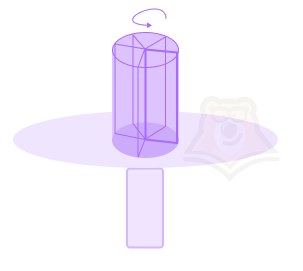
Похожий оптический эффект можно заметить, если посмотреть на двигатель самолета или винт вертолета: в статичном положении мы видим лопасти, а при работе они превращаются в круги. 

Таким же образом образуются любые тела вращения совершенно различных форм.

Наш эксперимент описывает тела вращения. 

Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 

Вращать можно любую фигуру и вокруг любой оси, тогда у нас будут получаться разные тела. 

Поверхность и ось вращения

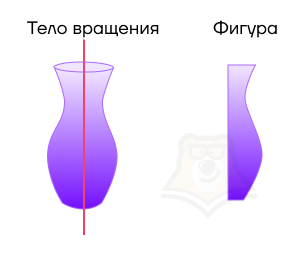
На примере выше мы видим вазу. Она состоит только из “оболочки” и полая внутри. В математике существует название и для этой оболочки. Называется она поверхностью вращения. 

Поверхность вращения — граница тела вращения. 

Иными словами, поверхность вращения является внешней оболочкой тела вращения и ограничивает его в пространстве. Как кожа у человека. 

Ось, вокруг которой мы вращаем фигуру, называется осью вращения. 

Ось вращения может по-разному располагаться относительно фигуры. 

• Ось совпадает с одной из ее сторон. 

Выше мы уже рассмотрели пример цилиндра и вазы. В их случае ось вращения лежит на одной из сторон фигуры, которую мы вращаем. 

• Ось лежит внутри фигуры. 

Например, ось может проходить через центр фигуры. Попробуем прокрутить  овал вокруг его горизонтальной оси, проходящей через центр.

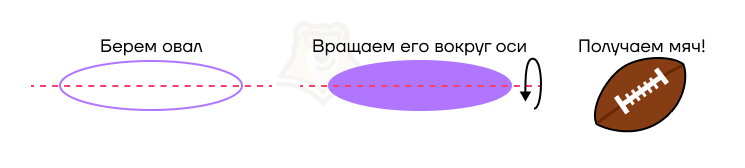
Мы получим эллипсоид. Эта фигура очень похожа на мяч для американского футбола.

• Ось лежит вне фигуры. 

Например, если мы будем вращать круг относительно оси, лежащей за его пределами, то получим “кольцо”.

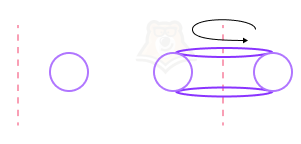
Такая фигура в математике называется тором. 

Причем тут тор и почему он без Локи? Разумеется, когда в математике упоминается тор, имеет в виду не скандинавский бог.  Тор — тело вращения, которое получается при вращении круга вокруг оси, лежащей за его пределами.

Среди тел вращения в математике наиболее часто встречаются цилиндр, конус, шар, эллипсоид и тор. Подробнее про некоторые из них можно прочесть в статьях «Цилиндр», «Конус», «Шар». 

Фактчек

• Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 
• Поверхность вращения — граница тела вращения. Ось вращения — ось, вокруг которой мы вращаем фигуру. 
• Ось, вокруг которой вращается фигура, может совпадать с одной из ее сторон, лежать внутри фигуры или за ее пределами. В каждом из этих случаев получаются различные тела вращения.
• В математике среди тел вращения наиболее часто встречаются цилиндр, конус, шар, эллипсоид и тор. 

Проверь себя

Задание 1. 
Что такое поверхность вращения?

1. Все тело вращения.
2. Граница тела вращения.
3. Ось вращения.
4. Основания тела вращения. 

Задание 2.
Что такое ось вращения?

1. Ось, вокруг которой вращается фигура, в результате чего получается тело вращения.
2. Центральная ось любой фигуры.
3. Ось, пересекающая плоскость фигуры перпендикулярно ей.
4. Любая прямая, расположенная любым способом в пространстве относительно фигуры. 

Задание 3. 
Из каких фигур можно получить тело вращения?

1. Только квадрат, прямоугольник и трапеция.
2. Только круг или овал.
3. Только параллелограмм.
4. Из любой.

Задание 4. 
Где может лежать ось вращения?

1. Принадлежать стороне фигуры.
2. Лежать “внутри” фигуры.
3. Лежать за пределами фигуры.
4. Все вышеперечисленное. 

Ответ: 1. – 2 2. – 1 3. – 4 4. – 4