Исследование функции с помощью производной

На этой странице вы узнаете

• Кто всегда протянет руку помощи в определении производной?
• Что такое сложная функция и зачем тут матрешка?
• Как никогда не ошибаться при решении задач с производными?

Теория теорией, а дифференцировать хочется всегда. Эта статья посвящена практике нахождения производных.

Производные основных функций

Должно быть, вы уже слышали о производной и даже пробовали взять её мозговым штурмом. При отрицательном ответе вам обязательно нужно прокатиться на американских горках в нашей статье «Производная». В ней рассмотрели основные понятия производной.

Главный вопрос этой статьи: как ее находить? Для этого существуют свои формулы и правила, которых необходимо придерживаться для правильного решения заданий. 

Ниже приведена таблица с формулами для нахождения производных основных функций. Применяя эти формулы, можно найти производную почти любой функции. 

Не пугайтесь, если вам покажется, что их много: это основные формулы, с помощью которых можно решить большинство задач.

1	C’ = 0, C = const
2	\((x^n)’ = n * x^{n — 1}, x > 0\)
3	\((a^x)’ = a^x * ln(a), a > 0, a \neq 1\)
4	\((e^x)’ = e^x\)
5	\((log_{a}x)’ = \frac{1}{x * ln(a)}, x > 0, a > 0, a \neq 1\)
6	\((ln(x))’ = \frac{1}{x}, x > 0\)
7	\((\sqrt{x})’ = \frac{1}{2\sqrt{x}}, x > 0\)
8	(sin(x))’ = cos(x)
9	(cos(x))’ = -sin(x)
10	\((tg(x))’ = \frac{1}{cos^{2}x}, x \neq \frac{\pi}{2} + \pi n, n \in Z\)
11	\((ctg(x))’ = -\frac{1}{sin^{2}x}, x \neq \pi n, n \in Z\)

Смотреть на формулы и учить их — это круто, прямо ощущаем себя великими учеными. Что может быть круче этого? Только применять их на практике. Рассмотрим несколько примеров нахождения производной. 

Пример 1. Найдите производную функции f(x) = 5. 

Решение: 5 — это число, то есть константа. Тогда, пользуясь первой формулой в таблице, получаем:

f'(x) = 5′ = 0. 

Ответ: 0

Пример 2. Найдите производную функции \(f(x) = x^4\)

Решение: В этом случае необходимо воспользоваться второй формулой из таблицы. 

\(f'(x) = (x^4)’ = 4 * x^{4-1} = 4 * x^3\)

Ответ: \(4x^3\)

Пример 3. Найдите производную функции \(f(x) = e^x\)

Решение: В этом случае необходимо воспользоваться четвертой формулой из таблицы. 

\(f'(x) = (e^x)’ = e^x\)

Ответ: \(e^x\)

Правила дифференцирования

С полной уверенностью можем сказать, что вам  встречались сложные функции. Даже намного сложнее, чем те, которые приведены в таблицах. Там и сумма, и произведение, и формула в формуле. Одним словом: ужас! Как брать производную, если перед функцией стоит коэффициент, или в функцию включено несколько разных выражений? На этот случай существуют правила дифференцирования. 

Кто всегда протянет руку помощи в определении производной? В сложных функциях невозможно пользоваться только формулами для нахождения производной. Если функция — усложнена коэффициентом,  — представлена в виде суммы, произведения или частного  — или является сложной функцией,  то для выбора правильной производной необходимо воспользоваться правилами дифференцирования. Они играют роль супергероев от мира производных. Рассмотрим их внимательнее.

1. Коэффициент можно вынести за знак производной. 

(k * f(x))’ = k * (f(x))’

Например, необходимо взять производную у функции f(x) = 6sin(x). Тогда, пользуясь правилом дифференцирования и таблицей, получаем ответ 6cos(x). 

2. Производная суммы (разности) равняется сумме (разности) производных. 

\((f(x) \pm g(x))’ = f'(x) \pm g'(x)\)

Найдем производную \(f(x) = 4x^5 — \sqrt{x} + cos(x)\).

\(f'(x) = (4x^5 — \sqrt{x} + cos(x))’ = (4x^5)’ — (\sqrt{x})’ + (cos(x))’ = 4 * 5 * x^{5 — 1} — \frac{1}{2\sqrt{x}} — sin(x)\)
\(f'(x) = 20x^4 — \frac{1}{2\sqrt{x}} — sin(x). \)

3. Производная произведения. 

(f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x)

Для примера возьмем производную функции f(x) = x² * ln(x)

f'(x) = (x² * ln(x))’ = (x²)’ * ln(x) + x² * (ln(x))’
\(f'(x) = 2x * ln(x) + x^2 * \frac{1}{x} = 2x * ln(x) + x\)

4. Производная частного. 

\((\frac{f(x)}{g(x)})’ = \frac{f'(x) * g(x) — f(x) * g'(x)}{g^{2}(x)}\)

Возьмем производную функции \(f(x) = \frac{e^x}{3x}\)

\(f'(x) = \frac{(e^x)’ * 3x — ex * (3x)’}{(3x)^2} = \frac{e^x * 3x — e^x * 3}{9x^2} = \frac{3e^x * (x-1)}{9x^2} = \frac{e^x * (x-1)}{3x^2}\)

5. Производная сложной функции. 

Сложная функция — это функция, внутри которой есть другая функция. 

Что такое сложная функция и зачем тут матрешка? Давайте представим матрешку: в одну большую куклу складывается куколка поменьше, а в нее еще меньше и так далее. Точно так же и с функцией: “внутри” одной функции может лежать другая функция.  Например, у нас есть две функции: \(\sqrt{x}\) и cos(x). А теперь попробуем поместить корень в функцию с косинусом, и получим \(cos(\sqrt{x})\). Это и будет сложная функция.

Чтобы найти производную сложной функции, необходимо найти производную “внутренней” функции и умножить ее на производную “внешней” функции. 

(f(g(x))’ = g'(x) * f'(g(x))

Найдем производную уже рассмотренной функции \(f(x) = cos(\sqrt{x})\). 

\(f'(x) = (cos(\sqrt{x}))’ = (\sqrt{x})’ * (cos(\sqrt{x}))’ = \frac{1}{2\sqrt{x}} * (-sin(\sqrt{x})) = -\frac{sin(\sqrt{x})}{2\sqrt{x}}\)

Исследование функции с помощью производной 

В задании нам может быть дана только функция без ее графика. Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене. 

В этом случае мы можем проанализировать поведение функции с помощью производной. 

Исследуем функцию f(x) = (x — 4)²(x + 11) + 4. 

Cначала возьмем производную от этой функции: 

f'(x) = ((x — 4)²(x + 11))‘ + 4′ = ((x — 4)²(x + 11))’ = ((x — 4)²)'(x + 11) + (x — 4)²(x + 11)’
f'(x) = 2(x — 4)(x + 11) + (x — 4)² * 1 = (x — 4)(2(x + 11) + (x — 4)) = (x — 4)(3x + 18)

Любое исследование функции с помощью производной начинается именно с дифференцирования функции. 

Теперь рассмотрим алгоритм нахождения точек минимума и максимума:

1 шаг. Нужно найти производную функции. 2 шаг. Найденную производную необходимо приравнять к 0 и решить полученное уравнение.  3 шаг. Расставить корни полученного уравнения на числовой прямой.  4 шаг. Определяем знаки производной на промежутках. Для этого необходимо подставить любое значение с выбранного промежутка в производную функции.  5 шаг. Определить, какие точки будут точками минимума (в них знак меняется с минуса на плюс), а какие — точками максимума (знак меняется с плюса на минус).

Найдем точки минимума и максимума в нашей функции. Поскольку производную мы уже взяли, можно сразу перейти ко второму шагу: 

(x — 4)(3x + 18) = 0
x = 4, x = -6.

Полученные значения х расставляем на числовой прямой: 

Теперь определим знаки на промежутках слева направо.

1. Возьмем точку -10 и подставим ее в производную функции: 
(-10 — 4)(3 * (-10) + 18) = (-14) * (-12) = 168. Производная на этом промежутке будет положительной. 

2. Возьмем точку 0 и подставим ее в производную функции: 
(0 — 4)(3 * 0 + 18) = (-4) * 18 = -72. Производная на этом промежутке будет отрицательной. 

3. Возьмем точку 5 и подставим ее в производную функции: 
(5 — 4)(3 * 5 + 18) = 33. Производная на этом промежутке будет положительной. 

Расставим полученные знаки на прямой: 

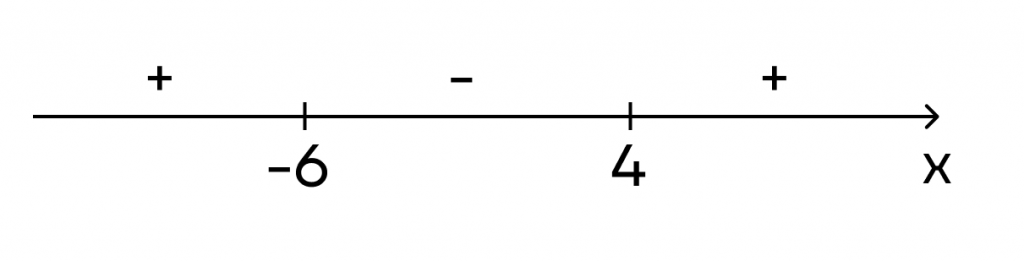
Остался последний пятый шаг. В точке -6 производная меняет знак с плюса на минус, значит, это точка максимума. В точке 4 производная меняет знак с минуса на плюс, значит, это точка минимума. 

Важно! Если в задании встречается формулировка “Найдите точку минимума (максимума) функции”, то необходимо пользоваться именно этим алгоритмом.

Но это не все выводы, которые уже можно сделать о функции. Вспомним, что функция возрастает, когда производная положительна, а убывает, когда производная отрицательна. Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать. 

Однако могут встретиться задания, в которых необходимо найти наибольшее или наименьшее значение функции на определенном интервале. 

Для выполнения таких заданий существует следующий алгоритм нахождения наибольшего и наименьшего значения функции.

Шаг 1. Найти производную функции.  Шаг 2. Найти точки минимума и максимума функции. Шаг 3. Определить, какие из точек минимума и максимума принадлежат заданному интервалу.  Шаг 4. Найти значение функции в отобранных в предыдущем шаге точках, а также в точках, которые являются границами заданного интервала. Для этого необходимо подставить точки в функцию (не в производную от функции).

Для примера найдем наибольшее значение функции f(x) = (x — 4)²(x + 11) + 4 на отрезке [-10; 0]. 

Первые два шага мы уже выполнили, когда рассматривали алгоритм нахождения точек минимума и максимума. Из них отрезку [-10; 0] принадлежит х = -6 — точка максимума. 

Теперь определим значение функции в трех точках: 

f(-10) = (-10 — 4)²(-10 + 11) + 4 = 196 + 4 = 200
f(-6) = (-6 — 4)²(-6 + 11) + 4 = 500 + 4 = 504
f(0) = (0 — 4)²(0 + 11) + 4 = 176 + 4 = 180

Наибольшее из полученных значений — это 504. Это и будет ответ. 

Как никогда не ошибаться при решении задач с производными? Может возникнуть вопрос, почему важно проверять значение функции и на границах отрезка? В заданиях ЕГЭ очень часто встречаются случаи, когда нужно найти наибольшее значение, и в интервале лежит точка максимума, или когда нужно найти наименьшее значение функции и в интервале лежит точка минимума. Логично будет проверить только экстремумы, поскольку в них, скорее всего, достигается наибольшее или наименьшее значение.  Однако стоит вспомнить, что мы не видим график функции и не можем с точностью определить, что в экстремуме достигается нужное нам значение. С помощью экстремумов мы можем описать поведение функции: где она возрастает, а где убывает. Но можно столкнуться с графиком, на котором граничная точка будет лежать выше или ниже точки экстремума. Тогда наибольшее или наименьшее значение будет достигаться именно в ней. Пример на картинке (красными линиями обозначены границы отрезка).

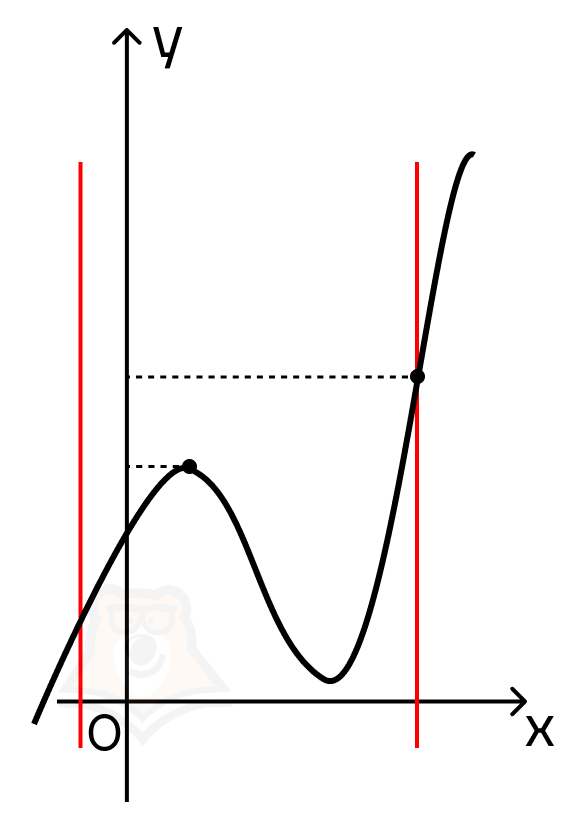
Подведем итог.
Как можно исследовать функцию с помощью производной?
С помощью производной можно с точностью сказать, на каких участках функция будет возрастать и убывать, сколько точек максимума и минимума у нее есть, какое наибольшее или наименьшее значение принимает функция на заданном участке. 

Фактчек

• Для нахождения производной необходимо пользоваться специальными формулами для производной. С их помощью можно найти производную любой из основных функций.
• Если функция усложнена коэффициентом, является сложной или представлена в виде суммы, произведения или частного, то необходимо пользоваться правилами дифференцирования. Они помогут правильно найти производную.
• Сложная функция — это функция, внутри которой есть другая функция. 
• С помощью производной можно исследовать функцию, а именно найти точки минимума и максимума, определить, на каких участках функция возрастает и убывает, найти наибольшее и наименьшее значение функции на заданном отрезке. 

Проверь себя

Задание 1.
Чему будет равна производная f(x) = 3?

1. 3;
2. 1;
3. 0;
4. Производную этой функции невозможно найти.

Задание 2. 
Чему будет равна производная f(x) = 5x²?

1. 10x;
2. 10x²;
3. 5x²;
4. 2x.

Задание 3.
Чему будет равна производная f(x) = 13x + 5 + x³?

1. 18 + 3x²;
2. 13 + 3x²;
3. 18;
4. 3x².

Задание 4.
Чему будет равна производная f(x) = ln(x)?

1. x
2. \(\frac{1}{x}\)
3. \(\frac{1}{2\sqrt{x}}\)
4. e^x

Задание 5.
Чему будет равна производная f(x) = tg(x)?

1. \(\frac{1}{cos^{2}(x)}\)
2. \(-\frac{1}{sin^{2}(x)}\)
3. \(-\frac{1}{cos^{2}(x)}\)
4. \(\frac{1}{sin^{2}(x)}\)

Ответы: 1. — 3 2. — 1 3. — 2 4. — 2 5. — 1