Числовые последовательности

На этой странице вы узнаете

• Как мы привыкаем к последовательностям на протяжении нашей жизни?
• Что такое золотое сечение?
• Что общего у числовых последовательностей, нейронных сетей и коллекционирования?

Что значит «действовать последовательно»? Мы делаем что-то по определенным принципам, не нарушаем правила. Все наши действия будут иметь логику, которую мы сможем отследить. В математике также можно составлять числа в строгом порядке. Называться такие ряды будут последовательностями. 

Понятие последовательности 

Посмотрим на несколько рядов чисел и порассуждаем.

По какому принципу составлен ряд чисел 1, 2, 3, 4, 5 и т.д.? Все просто: к каждому новому числу прибавляют единицу.
А какой принцип в ряде чисел 2, 4, 6, 8 и т.д.? Здесь к каждому новому числу прибавляют 2.
Что можно сказать про ряд 2, 4, 8, 16, 32 и т.д.? Каждое новое число умножают на 2. 

Все приведенные выше ряды чисел будут называться последовательностью. Как описать ее одним термином?

Ненадолго отвлечемся и вспомним функции чисел. Разберем функцию f(x)=x+1.
Если x=0, то f(x)=1.
Если x=1, то f(x)=2.
Если x=2, то f(x)=3.
Если x=3, то f(x)=4.
Внимательно посмотрим на значения функции: это и будет наша первая последовательность 1, 2, 3, 4, 5. Мы можем сделать вывод, что последовательность можно задать с помощью функции. 

На самом деле, любая последовательность и есть функция. Теперь дадим определение. 

• Последовательность — функция, заданная на множестве натуральных чисел или его части. 

То есть подставлять в такую функцию можно только натуральные числа. 

Подробнее про функцию, ее значение, область определения и другие свойства можно прочесть в статье «Определение и график функции». 

Аргумент будет обозначать порядковый номер числа в последовательности. Первое число в последовательности будет задаваться х = 1, второе число х = 2, n число как х = n. 

Числа, которые образуют последовательность, — это члены последовательности. И у каждого члена последовательности есть свой порядковый номер. 

Как же обозначаются члены последовательности? Не будем же мы каждый раз писать «двадцатый член последовательности» или что-то подобное?
Для членов последовательности существует свое обозначение: \(a_n\), где индекс после буквы а обозначает порядковый номер члена последовательности. 

Например, 

• а₁ — первый член последовательности, 
• а₂₀ — двадцатый член последовательности, 
• а₁₀₀ — сотый член последовательности и так далее. 

Таким образом можно обозначить любой член последовательности. 

Как мы привыкаем к последовательностям на протяжении нашей жизни? Вспомним считалочки, которые мы использовали в играх в детстве: «Раз, два, три, четыре, пять, вышел зайчик погулять».  Первая строчка многих подобных считалочек — это последовательность натуральных чисел 1, 2, 3, 4, 5. Дальше в школе на уроках физкультуры нас распределяют по командам, присваивая каждому свой номер. И это тоже последовательность. Потом мы поступаем в вуз и попадаем в списки абитуриентов, тоже — в еще одну последовательность.

Мы узнали, что такое числовая последовательность и как обозначить ее члены, но какими способами можно задать последовательность. 

Способы задания числовой последовательности

Первый способ — это указать все члены последовательности. Однако он не всегда удобен, поскольку в последовательности может быть бесконечное количество членов. 

Второй способ мы уже использовали — это задать общую формулу. Тогда можно будет найти любой член последовательности. В этом случае нужно будет подставить порядковый номер члена последовательности в формулу. 

Допустим, дана последовательность \(a_n=3n+40\), и нам нужно найти третий член последовательности. Тогда нужно подставить \(n = 3\) в формулу:
\(a_3=3*3+40=9+40=49\). 

Аналогичным способом можно будет найти любой член в данной последовательности. 

Рассмотрим еще пример. Что мы можем сказать про последовательность чисел 2, 4, 12, 32, 88 и так далее? Определенный закон здесь вывести достаточно сложно. Все потому, что следующий член последовательности зависит от предыдущего. 

Обратим внимание на третий член последовательности: \(12=2*6=2(2+4)\). А если посмотреть на четвертый член последовательности? \(32=2*16=2(4+12)\). 

И так с каждым членом последовательности: он равен удвоенной сумме двух предыдущих членов. 

Это еще один способ задания последовательности, когда используется рекуррентная формула. Ее особенность в том, что каждый член последовательности выражен с помощью предыдущих членов последовательности. 

Одним из примеров такой последовательности будут числа Фибоначчи. Это последовательность, в которой первые два члена равны 1, а все следующие являются суммой двух предшествующих им. 

Числа Фибоначчи выглядят так: 1, 1, 2, 3, 5, 8, 13, 21 и так далее.

Как задать их с помощью рекуррентной формулы? Допустим, мы хотим найти член an в этой последовательности. Мы знаем, что для этого нужно сложить два предыдущих члена, то есть \(a_{n-1}\) и \(a_{n-2}\). Вот мы и получили формулу.
\(a_n=a_{n-1}+a_{n-2}\). 

Что такое золотое сечение? Золотое сечение — это пропорциональное деление отрезка на неравные части. При этом весь отрезок относится к большей части, как меньшая часть этого отрезка относится к большей его части. Золотое сечение можно представить в виде «завитка», который вписан в прямоугольник. Прямоугольник будет делиться на квадраты, стороны которых равны числам Фибоначчи.

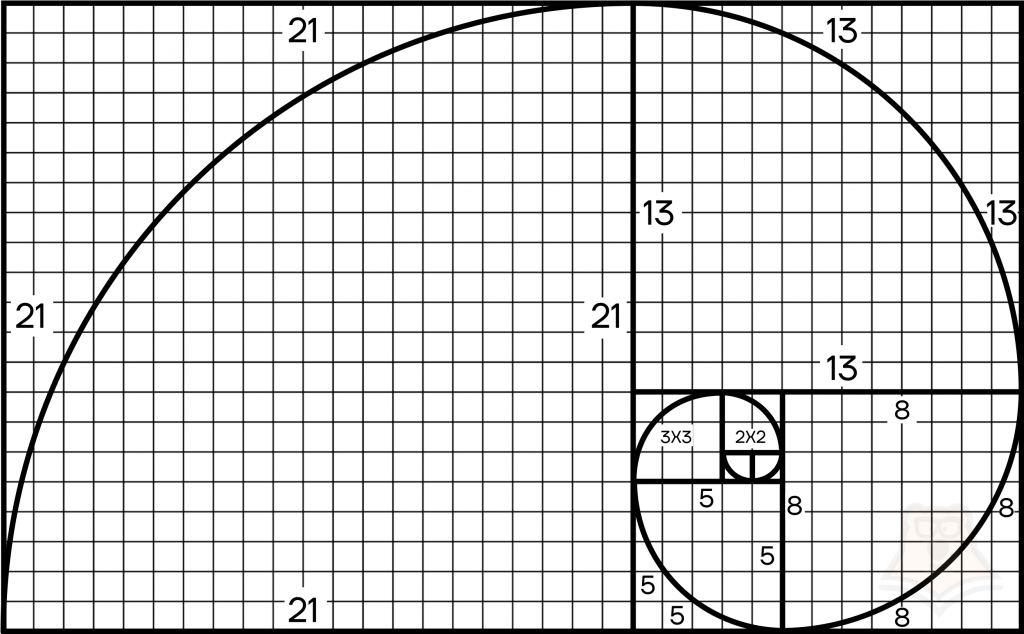
Принцип золотого сечения позволяет построить гармоничную композицию, а значит, применяется в архитектуре и искусстве. Более того, его можно встретить в природе. Форма ракушек, завитки ростков, семена подсолнуха, шишки, даже ураган (если посмотреть на него сверху) имеют форму золотого сечения или приближенную к нему.

Числовые последовательности можно разделить не только по способам задания, но и по виду. Рассмотрим, какие они могут быть.

Виды числовых последовательностей

Возьмем обычную последовательность натуральных чисел 1, 2, 3, 4, 5, …, a_n. Мы можем сказать, что каждый следующий член последовательности больше, чем предыдущий. Такие последовательности называются возрастающими. 

Даже без знания специальных формул, просто понимая, что такое возрастающая последовательность, можно решить задачи из экзамена. Для примера разберем задание №14 из ОГЭ:

Задание. В первом ряду театра 12 мест, в каждом следующем на 2 больше. Сколько мест в шестом ряду?

Решение. Раз в каждом следующем ряду на 2 места больше, мы решаем задачу на последовательность, выпишем ее: каждое следующее число на два больше предыдущего.

12, 14, 16, 18, 20, 22, 24, 26, 28, 30, …

Нам нужен 6 ряд, следовательно, берем 6 число в последовательности, это число 22.

Ответ: 22

Если перевернуть возрастающую последовательность и получить 5, 4, 3, 2, 1, …, a_n — эта последовательность будет называться убывающей. Для такой последовательности обязательно, чтобы каждый следующий член был меньше, чем предыдущий. 

Что, если мы просто будем менять знак числа? Например, −1, 1, −1, 1 и так далее? Тогда последовательность будет ни убывающей и ни возрастающей. 

Такую последовательность можно задать с помощью формулы \(a_n=(-1)^n\). 

Что общего у числовых последовательностей, нейронных сетей и коллекционирования? В 1964 году математик Нил Джеймс Александр Слоун писал диссертацию по нейронным сетям и наткнулся на числовую последовательность, вычислив среднее число шагов, которое должен пройти сигнал по сети из 1,2,3, … нейронов. Получилась последовательность: 0, 1, 8, 78, 944, 13800, 237432, … Слоун решил изучить научную литературу, чтобы найти в ней свойства получившейся последовательности, заодно, заинтересовавшись, он выписывал другие интересные попадавшиеся ему последовательности. Так Слоун начал коллекционировать последовательности, он даже получал письма с новыми экземплярами для своей коллекции. В 1973 году появился «Справочник целочисленных последовательностей», а в 1995 году вышла уже одноименная энциклопедия и в 1996 была создана онлайн-энциклопедия целочисленных последовательностей, OEIS.

Разумеется, не все последовательности бывают бесконечными. Ранее мы рассматривали только бесконечные последовательности: в них можно было подставить любое значение n. 

Возьмем последовательность простых однозначных чисел: 2, 3, 5, 7. Больше однозначных чисел нет — продолжить последовательность мы не можем. 

Последовательность, в которой ограничено количество членов, будет называться конечной последовательностью. Если же в последовательности не ограничено количество членов, и их можно задавать до бесконечности, то такая последовательность будет называться бесконечной последовательностью. 

Разберем еще одну задачу из экзамена, которую можно решить просто зная, что такое возрастающая и ограниченная последовательность. Задача №20 из ЕГЭ по базовой математике.

Задание. Вася начал занятия спортом с 15 минут ежедневно, и каждый день увеличивал время на 10 минут. Вася закончит занятия, когда время тренировки составит 1 часа 25 минут. На какой день это произойдет?

Решение. Так как время увеличивается и при этом по условию в какой-то момент Вася закончит свои тренировки, мы будем решать задачу на возрастающую и ограниченную числовую последовательность.

Нам нужно выписать эту последовательность и остановиться в тот момент, когда какой-то член последовательности станет равным 1 часу 25 минутам (85 минутам):

15, 25, 35, 45, 55, 65, 75, 85

Выписав последовательность, нужно понять на какой день это произошло, то есть на каком по счету месте стоит подходящее на время

Ответ: 8

Мы разобрали понятие числовых последовательностей и посмотрели задачи, которые можно решить, обладая только пониманием этого понятия. Но также есть задания, которые решаются более сложно с использованием специальных формул. Об этом вы сможете узнать в статье «Арифметическая прогрессия».

Термины

Аргумент –  переменная величина у функции, которая может менять свое значение. 

Значение функции – числовое значение, которое получается при подстановке в исходную функцию какого-то числа вместо независимой переменной х.

Натуральные числа – числа, употребляемые при счете.

Простые числа – числа, которые делятся только на себя и на единицу.

Фактчек

• Последовательность — функция, заданная на множестве натуральных чисел или его части. 
• Каждый член последовательности имеет свой номер, который отображается в индексе. Например, a1 — первый член последовательности, а a25 — двадцать пятый. 
• Последовательность можно задать несколькими способами. Во-первых, выписать все члены последовательности. Во-вторых, задать общую формулу. В-третьих, задать рекуррентную формулу. 
• Рекуррентная формула — это формула, в которой каждый следующий член последовательности зависит от предыдущих. То есть чтобы получить новый член последовательности, мы обязательно должны знать предыдущие. Ярким примером такой последовательности являются числа Фибоначчи, где каждое число является суммой двух предыдущих. 
• Последовательности бывают возрастающими и убывающими. В возрастающих последовательностях каждый следующий член больше предыдущего, а в убывающей каждый следующий член последовательности меньше предыдущего. В бесконечных последовательностях не ограничено количество членов. А в конечных последовательностях количество членов ограничено. 

Проверь себя

Задание 1.
Какая из представленных последовательностей конечна?

1. Числа Фибоначчи.
2. Четные положительные числа.
3. Нечетные трехзначные числа.
4. Нечетные отрицательные числа. 

Задание 2.
Какая последовательность является убывающей?

1. 10, 9, 8, 7, 6, 5, …, a_n
2. Числа Фибоначчи
3. 1, 2, 3, 4, 5, …, a_n
4. 1, 3, 5, 7, 9, …, a_n 

Задание 3.
Какая последовательность является возрастающей?. 

1. 100, 90, 80, …, a_n
2. 12, 13, 14, …, a_n
3. Числа Фибоначчи
4. −1, −2, -3, …, a_n

Задание 4.
Какая последовательность соответствует последовательности Фибоначчи? 

1. 1, 2, 3, 4, 5, …
2. 1, 1, 2, 3, 5, 8, …
3. 1, 4, 9, 16, 25, …
4. 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), …

Ответы: 1. — 3; 2. — 1; 3. — 3; 4. — 2.