Дроби

На этой странице вы узнаете

• Получится ли разделить два яблока поровну на троих человек?
• Как связаны дроби и музыка?
• Почему десятичные дроби так важны на спортивных соревнованиях?

Как продать часть стада овец или купить пол-литра молока? Выполняя такие, казалось бы, простые действия, человек впервые столкнулся с дробями. И сейчас, приходя в магазин, кафе или покупая билеты в музей, мы постоянно сталкиваемся с частями чего-то целого: детский билет составляет какую-то часть от взрослого, а сезон сериала – часть от него. 

Таким образом, говоря о дробях, мы имеем в виду не все число, а какую-то его часть – долю, например, четверть – это \(\frac{1}{4}\), половина – это \(\frac{1}{2}\) и так далее: количество частей, которые мы берем, называют числителем дроби и пишут выше черты; количество частей, на которое мы делим целое число, называют знаменателем дроби и пишут под чертой. 

Важно заметить, что, говоря о делении на части, мы подразумеваем равные части какой-либо величины. 

Но как можно взять лишь часть от числа? Дробь можно понимать как деление, где числитель – делимое, а знаменатель – делитель. 

Обыкновенная дробь – запись вида \(\frac{m}{n}\), где m,n любые натуральные числа, а дробная черта – знак деления.

Возьмем, например, дробь \(\frac{4}{7}\). В данном случае мы делим, например, тортик на семь частей и потом берем только четыре из них. Аналогично с дробью \(\frac{5}{12}\): делим тортик на двенадцать кусочков и берем пять из них. 

Мы разобрались, что такое дроби, теперь посмотрим, как с ними работать. 

Правила работы с обыкновенными дробями

Можно ли как-то изменять числитель и знаменатель, при этом не меняя значение самой дроби? 

Мы можем умножать числитель и знаменатель на любое число (целое или дробное), важно только, что умножать надо на одно и то же число, тогда числитель и знаменатель будут другими, но сама дробь не изменится. 

Например, мы купили пирог среднего размера и разрезали его на какое-то количество равных частей. Если же мы возьмем пирог побольше, то чтобы получить кусочки такого же веса и размера, мы должны также увеличить количество частей, на которые мы его разрежем. 

Рассмотрим дробь \(\frac{3}{5}\).

• Попробуем умножить числитель и знаменатель на 2, получим дробь \(\frac{3*2}{5*2}=\frac{6}{10}\), при этом значение дроби не изменится.
• Аналогично умножим исходную дробь на 4, получим \(\frac{3*4}{5*4}=\frac{12}{20}\). 

Это правило называется основным свойством дроби: 

Если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же число, неравное нулю, то значение дроби не изменится.

Остановимся подробнее на делении числителя и знаменателя дроби на одинаковые числа. 

Как мы уже говорили, дробь \(\frac{15}{20}\) может быть равна как \(\frac{3}{4}\), так и \(\frac{30}{40}\). Но с какой из этих дробей удобнее работать? Конечно, удобнее когда числа как можно меньше, то есть самая лучшая запись этой дроби \(\frac{3}{4}\). 

На самом деле, это справедливо и в жизни: если мы, например, хотим отрезать \(\frac{15}{20}\) или \(\frac{3}{4}\) от всего куска ткани, гораздо удобнее будет разделить ее на четыре части и использовать три из них, чем делить на двадцать частей и использовать пятнадцать.

В этой записи числитель и знаменатель взаимно простые числа, то есть у них больше нет общих делителей. Чтобы получить такую дробь, мы сократили исходную \(\frac{15}{20}\). 

Сокращение дроби – деление ее числителя и знаменателя на их наибольший общий делитель.

Наибольший общий делитель – максимальный делитель двух чисел.

Подробнее о наибольшем общем делителе можно прочитать в статье «Действия с натуральными числами».

Например, в дроби \(\frac{32}{64}\) мы можем разделить числитель и знаменатель и на 2, и на 4, и на 8, и на 16. Но для получения взаимно простых чисел в числителе и знаменателе мы должны разделить их на 32, что является наибольшим общим делителем 32 и 64. Сократив дробь на 32, мы получаем \(\frac{1}{2}\). 

Получится ли разделить два яблока поровну на троих человек? Мы знаем, что просто поделить два яблока на три части никак не получится, но как тогда быть? Можно поделить каждое яблоко на шесть равных частей и каждому дать по четыре части, или можно каждое яблоко разделить на три, девять или двенадцать частей и каждому дать по две, шесть или восемь долек. То есть надо просто разрезать яблоко на такое количество кусков, чтобы оно делилось на три. Таким образом, каждый получит нецелое яблоко, но зато их порции будут равны.

До сих пор мы работали только с дробями, у которых числитель меньше знаменателя, такие дроби называются правильными. Их значение меньше 1, поскольку мы делим меньшее число на большее. Но может ли дробь быть больше единицы? 

Далее мы поговорим о том, как работать с неправильными дробями, то есть с теми, у которых числитель больше знаменателя. 

Неправильные дроби 

Неправильная дробь – это дробь, значение которой больше или равно единице.

В неправильных дробях числитель больше (или равен) знаменателя. Тогда, разделив большее число на меньшее, мы обязательно получим значение больше единицы. 

При этом значение дроби может быть и больше 2, 3, 10 и так далее, в зависимости от чисел в числителе и знаменателе. 

Например, дробь \(\frac{2}{4}=2\), а вот \(\frac{100}{5}=20\). 

Исходя из определения, в неправильной дроби всегда есть целая часть, то есть ее можно представить как целое число и плюс еще какая-то правильная дробь, которая обязательно меньше единицы. Такая форма записи называется смешанным числом.

Как же превратить неправильную дробь в смешанное число?

1. Разделить с остатком числитель на знаменатель.
2. Частное от этого деления будет целой частью, остаток пойдет в числитель дробной части, а знаменатель же не меняется.

Подробнее про деление с остатком можно узнать в статье «Действия с натуральными числами».

Например, рассмотрим дробь \(\frac{21}{16}\). 

Разделим числитель на знаменатель с остатком: \(21:16 = 1\) (ост. 5) 

Запишем смешанной число. Сначала пишем частное, то есть результат деления, – целая часть, далее дробь, где остаток – числитель дробной части, знаменатель не меняется: \(\frac{21}{16} = 1\frac{5}{16}\).

Мы разобрались, как переводить из неправильной дроби в смешанное число, но что делать, если необходимо выполнить обратное действие: перевести смешанное число в неправильную дробь? Здесь все еще проще! 

Рассмотрим дробь \(2\frac{3}{7}\).

Вернемся к нашему примеру на деление с остатком: в данном случае мы уже знаем и делитель (знаменатель дробной части), и частное (целая часть), и остаток (числитель дробной части), но чтобы перевести смешанное число в неправильную дробь, нам надо знать числитель этой дроби, то есть делимое. 

Запишем это в математическом виде: \(x:7 = 2\) (ост. 3)
Надо найти x: \(x = 7* 2 + 3 = 17\)
Значит \(2\frac{3}{7}=\frac{17}{7}\)

Чтобы перевести смешанное число в неправильную дробь, необходимо:

1. Умножить знаменатель дробной части на целую часть.
2. Прибавить к этому произведению числитель дробной части.
3. Внести получившееся значение в числитель неправильной дроби.
4. Знаменатель неправильной дроби равен знаменателю дробной части, он переписывается без изменений.

Мы разобрались, как работать с неправильными дробями, дальше посмотрим, какие арифметические операции можно производить с дробями и как это правильно делать. 

Арифметические операции с дробями 

Дроби так же как и целые числа можно складывать между собой, вычитать, делить и умножать. Давайте разберемся, как действовать в различных случаях. 

Сложение и вычитание дробей с одинаковыми знаменателями 

При сложении (вычитании) дробей с одинаковыми знаменателями мы складываем (вычитаем) только их числители, не меняя знаменатель. 

Например:

1. \(\frac{4}{11}+\frac{5}{11}=\frac{4+5}{11}=\frac{9}{11}\)
2. \(\frac{11}{17}+\frac{22}{17}=\frac{11+22}{17}=\frac{33}{17}\)
   Переведем получившуюся дробь в смешанное число:
   \(33:17 = 1\) (ост. 16)
   \(\frac{33}{17}=1\frac{16}{17}\)
3. \(\frac{11}{12}-\frac{5}{12}=\frac{6}{12}=\frac{1}{2}\)
   Здесь мы сократили дробь, разделив числитель и знаменатель на 6.

Сложение и вычитание дробей с разными знаменателями 

Дроби с разными знаменятелями складывать нельзя.

Но как тогда действовать, если надо сложить, например, \(\frac{5}{6}\) и \(\frac{3}{10}\)?

Первое, что мы делаем, приводим дроби к общему знаменателю, то есть, пользуясь основным свойством дроби, домножаем числитель и знаменатель каждой дроби на какое-то число так, чтобы в итоге в знаменателях получилось одно и то же значение.

Общий знаменатель – наименьшее положительное число, кратное знаменателям данных дробей.

Первым делом мы должны найти наименьшее общее кратное (НОК). 

Наименьшее общее кратное – минимальное число, которое делится на данные числа.

Лучше разобраться в том, что такое наименьшее общее кратное, и как его искать, вам может помочь наша статья «Действия с натуральными числами».

Вернемся к примеру: \(\frac{5}{6}+\frac{3}{10}\). Наименьшим общим кратным 6 и 10 является 30.

Значит, мы нашли общий знаменатель, он равен 30.

Получив 30 в знаменателе, мы домножили знаменатель первой дроби на \(5: 5* 6 = 30\); а знаменатель второй дроби умножили на \(3: 10* 3 = 30\).

Если мы домножили знаменатели, значит, по основному свойству дроби, должны домножить и числители на те же самые числа: \(\frac{5*5}{30}+\frac{3*3}{30}=\frac{25}{30}+\frac{9}{30}\).

Но как называются числа, на которые мы только что умножали числители и знаменатели дроби?

Дополнительный множитель – это натуральное число, на которое нужно умножить числитель и знаменатель дроби, чтобы привести ее к другому знаменателю. 

В данном случае 5 и 3 – дополнительные множители. 

Получив общий знаменатель, мы можем сложить дроби по правилу сложения дробей с общим знаменателем: \(\frac{25}{30}+\frac{9}{30}=\frac{25+9}{30}=\frac{34}{30}=1\frac{4}{30}\)

Таким образом, мы получили алгоритм сложения и вычитания дробей с разными знаменателями:

1. Найти общий знаменатель складываемых дробей.
2. Найти дополнительный множитель каждой дроби.
3. Домножить числитель и знаменатель каждой дроби на ее дополнительный множитель, таким образом приводя дроби к одному знаменателю.
4. Сложить/вычесть получившиеся дроби.

Сложение и вычитание смешанных чисел 

При сложении (вычитании) смешанных чисел удобно каждое из них сначала перевести в неправильную дробь, а затем сложить (вычесть) получившиеся дроби. 

Например, \(2\frac{1}{4}+3\frac{2}{5}\). 

Сначала переведем каждое смешанное число в неправильную дробь: 

\(2\frac{1}{4}=\frac{2*4+1}{4}=\frac{9}{4}\)
\(3\frac{2}{5}=\frac{3*5+2}{5}=\frac{17}{5}\)

Сложим получившиеся дроби: 

1. Найдем общий знаменатель: НОК(4,5) = 20
2. Найдем дополнительные множители: для первой дроби – \(20:4 = 5\); для второй – \(20:5 = 4\).
3. Домножим числитель и знаменатель каждой дроби на ее дополнительный множитель: \(\frac{9*5}{4*5}+\frac{17*4}{5*4}\)
4. Сложим получившиеся дроби: \(\frac{45}{20}+\frac{68}{20}=\frac{113}{20}=5\frac{13}{20}\).

Сложение и вычитание обыкновенной дроби и смешанного числа

В данном случае мы переводим смешанное число в неправильную дробь и затем складываем (вычитаем) получившиеся дроби.

Например, \(1\frac{5}{9}+\frac{1}{3}\).

\(1\frac{5}{9}=\frac{1*9+5}{9}=\frac{14}{9}\)

Сложим получившиеся дроби: 

1. Найдем общий знаменатель: НОК(3,9) = 9
2. Найдем дополнительные множитель: для первой дроби – \(9:9= 1\); для второй – \(9:3= 3\).
3. Домножим числитель/ и знаменатель каждой дроби на ее дополнительный множитель: \(\frac{14*1}{9*1}+ \frac{1*3}{3*3}\)
4. Сложим получившиеся дроби: \(\frac{14}{9}+\frac{3}{9}=\frac{17}{9}=1\frac{8}{9}\).

Сложение и вычитание обыкновенной дроби и целого числа

Чтобы сложить/вычесть целое число и дробь, нужно целое число представить в виде дроби. 

Как это сделать? При делении на единицу любое число остается неизменным, следовательно, целое число можно представить в виде дроби, где в числители стоит это число, а в знаменателе – единица. Например, \(2=\frac{2}{1}; 5=\frac{5}{1}\).

Представив таким образом целое число, мы приходим к сложению (вычитанию) двух дробей с разными знаменателями.

Рассмотрим пример \(6+\frac{12}{5}=\frac{6}{1}+\frac{12}{5}\).

Сложим получившиеся дроби: 

1. Найдем общий знаменатель: НОК(1,5) = 5
2. Найдем дополнительные множитель: для первой дроби – \(5:1= 5\); для второй – \(5:5= 1\).
3. Домножим числитель и знаменатель каждой дроби на ее дополнительный множитель: \(\frac{6*5}{1*5}+ \frac{12*1}{5*1}\)
4. Сложим получившиеся дроби: \(\frac{30}{5}+\frac{12}{5}=\frac{42}{5}=8\frac{2}{5}\).

Сложение и вычитание целого числа и смешанного числа

При сложении (вычитании) смешанного числа и целого числа мы не меняем дробную часть смешанного числа, складываем (вычитаем) только целые части.

Например, \(3\frac{1}{6}-2=(3-2)\frac{1}{6}=1\frac{1}{6}\).

Мы разобрались, как складывать и вычитать дроби, теперь посмотрим на операции умножения и деления. 

Умножение обыкновенных дробей

При умножении обыкновенных дробей мы должны умножить числитель первой дроби на числитель второй; знаменатель первой дроби – на знаменатель второй. Затем при необходимости сократить дробь.

Например, \(\frac{9}{14}*\frac{2}{3}=\frac{9*2}{3*14}=\frac{18}{42}=\frac{3}{7}\).

На самом деле, производить сокращение дроби можно было еще на втором шаге, например, 2 и 14 разделить на 2, а 9 и 3 на 3. 

\(\frac{9}{14}*\frac{2}{3}=\frac{9*2}{3*14}=\frac{9*1}{3*7}=\frac{3*1}{1*7}=\frac{3}{7}\).

Умножение обыкновенной дроби на смешанное число

При умножении обыкновенной дроби на смешанное число действуем по правилу умножения дробей, но перед выполнением умножения необходимо перевести смешанное число в неправильную дробь. 

Рассмотрим пример, \(2\frac{4}{11}*\frac{1}{2}\).

\(2\frac{4}{11}+\frac{4}{11}=\frac{26}{11}\).

\(\frac{26}{11}*\frac{1}{2}=\frac{26*1}{11*2}=\frac{26}{22}=\frac{13}{11}\).

Умножение обыкновенной дроби на целое число

При умножении обыкновенной дроби на целое число сначала представим целое число в виде дроби, а затем умножим дробь на дробь.

Например, \(2*\frac{3}{5}=\frac{2}{1}*\frac{3}{5}=\frac{3*2}{5*1}=\frac{6}{5}=1\frac{1}{5}\).

Умножение смешанных чисел

В данном случае начинаем с того, что переводим смешанные числа в неправильные дроби, а затем получившиеся дроби умножаем. 

Например, \(1\frac{1}{6}*2\frac{2}{7}\):

\(1\frac{1}{6}=\frac{1*6+1}{6}=\frac{7}{6}\)
\(2\frac{2}{7}=\frac{2*7+2}{7}=\frac{16}{7}\)
\(\frac{7}{6}*\frac{16}{7}=\frac{7*16}{6*7}=\frac{16}{6}=\frac{8}{3}=2\frac{2}{3}\)

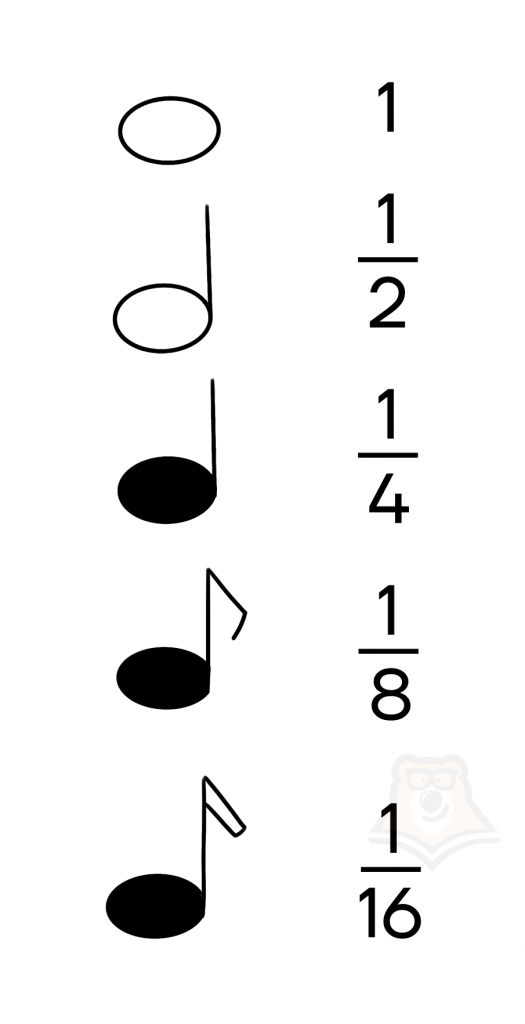
Как связаны дроби и музыка? Ноты в музыке отличаются по длительности звучания. Есть целая нота, половинная (\(\frac{1}{2}\)), четвертная (\(\frac{1}{4}\)), восьмая (\(\frac{1}{8}\)) и шестнадцатая (\(\frac{1}{16}\)).

Деление обыкновенных дробей

При делении одной обыкновенной дроби на другую необходимо перевернуть местами числитель и знаменатель делителя и затем умножить исходное делимое на получившийся делитель (это все равно, что умножить первую дробь на перевернутую вторую). 

Например, \(\frac{7}{8}:\frac{3}{12}=\frac{7}{8}*\frac{12}{3}=\frac{7*12}{8*3}=\frac{84}{24}=\frac{7}{2}\).

Деление обыкновенной дроби и целого числа

При делении обыкновенной дроби и целого числа нужно целое число представить в виде дроби и далее произвести деление по правилу деления обыкновенных дробей. 

Рассмотри пример, \(\frac{2}{9}:2=\frac{2}{9}:\frac{2}{1}=\frac{2}{9}*\frac{1}{2}=\frac{2*1}{9*2}=\frac{1}{9}\).

Деление обыкновенной дроби и смешанного числа

Переводим смешанное число в неправильную дробь. Затем делим обыкновенные дроби. 

Например, \(3\frac{4}{2}:\frac{7}{8}\):

\(2\frac{7}{8}=\frac{2*8+7}{8}=\frac{23}{8}\)
\(\frac{3}{4}:\frac{23}{8}=\frac{3}{4}*\frac{8}{23}=\frac{3*8}{4*23}=\frac{3*2}{1*23}=\frac{6}{23}\)

Деление смешанных чисел

Сначала переводим смешанные числа в обыкновенные дроби, и затем производим деление.

Например, \(2\frac{4}{11}:1\frac{1}{8}\):

\(2\frac{4}{11}=\frac{2*11+4}{11}=\frac{26}{11}\)
\(1\frac{1}{8}=\frac{1*8+1}{8}=\frac{9}{8}\)
\(\frac{26}{11}:\frac{9}{8}=\frac{26}{11}*\frac{8}{9}=\frac{26*8}{11*9}=\frac{192}{99}=1\frac{93}{99}\)

В ЕГЭ по базовой математике в задании №14 может встретиться пример на выполнение арифметических операций с обыкновенными дробями. 

Задание. Найдите значение выражения: \(1\frac{9}{14}: (\frac{5}{4}-\frac{3}{7})\).

Решение. Сначала выполним действие в скобках: \(\frac{5}{4}-\frac{3}{7}\)
1. Найдем общий знаменатель: НОК\((4,7) = 28\)
2. Найдем дополнительные множители: для первой дроби – \(28:4= 7\); для второй – \(28:7= 4\).
3. Домножим числитель и знаменатель каждой дроби на ее дополнительный множитель: \(\frac{5*7}{4*7}- \frac{3*4}{7*4}\)
4. Вычтем получившиеся дроби: \(\frac{35}{28}-\frac{12}{28}=\frac{23}{28}\).

Выполним второе действие: \(1\frac{9}{14}:\frac{23}{28}=\frac{1*14+9}{14}*\frac{28}{23}=\frac{23}{14}*\frac{28}{23}=\frac{28}{14}=2\)

Ответ: 2

Сравнение дробей

Бывает, что необходимо сравнить между собой несколько дробей. С этим легко справиться после изучения арифметических операций над дробями.

Сравнение дробей с одинаковыми знаменателями

Если у двух дробей одинаковые знаменатели, то больше из них будет та, у которой больше числитель.

Рассмотрим пример. Необходимо сравнить \(\frac{5}{7}\) и \(\frac{2}{7}\) . Мы знаем, что \(5>2\), значит, \(\frac{5}{7}>\frac{2}{7}\) .

Сравнение дробей с разными знаменателями

Если у дробей разные знаменатели, то сначала их надо привести к общему знаменателю, как мы делали при сложении дробей с разными знаменателями, а потом сравнить. Больше из них будет так, у которой больше числитель.

Рассмотрим пример. Необходимо сравнить \(\frac{1}{8}\) и \(\frac{2}{5}\). НОК \(8\) и \(5\) равен \(40\), это и будет общий знаменатель. Значит, нам необходимо домножить числитель первой дроби на \(5\), а числитель второй дроби на \(8\). Тогда мы получим \(\frac{5}{40}\) и \(\frac{2*8}{40}=\frac{16}{40}\). Мы знаем, что \(16>5\), поэтому \(\frac{5}{40}<\frac{16}{40}\) и, следовательно, \(\frac{1}{8}<\frac{2}{5}\).

Таким образом, мы получили алгоритм сравнения дробей с разными знаменателями.

1. Найти общий знаменатель.
2. Привести обе дроби к общему знаменателю.
3. Сравнить между собой числители полученных дробей.
4. Сделать вывод о том, какая дробь больше.

Обыкновенные дроби хотя и довольно просты при счете, но их не всегда удобно использовать. Например, при счете на калькуляторе или при использовании весов. В таких случаях переходят к десятичным дробям. 

Десятичные дроби

Десятичная дробь – дробь, имеющая в знаменателе \(10, 100, 1000\) и т.д. Такие дроби записываются в строчку, целая часть отделяется от дробной запятой. 

Десятичными дробями, так же как и обыкновенными, обозначают часть чего-то целого; три четверти – \(0,75\), пятая часть – \(0,2\), половина – \(0,5\). 

Положение цифр в дробной части называется разрядом. Мы можем округлять десятичные дроби до нужного нам разряда, подробнее об этом можно прочитать в статье «Действия с числами». 

Десятичные дроби бывают трех видов: 

• Конечные: такие дроби имеют конечное число цифр после запятой. Например, 4,2 или 5,125.
• Бесконечные: данные дроби имеют бесконечное число цифр после запятой. Например, число π = 3,141592… или экспонента e = 2,71828… .
• Бесконечные периодические: у таких дробей бесконечная последовательность цифр после запятой, начиная с какого-то момента, представляет собой повторяющуюся комбинацию цифр. Например, 3,122222… или 0,0056565656… . Период также записывает в скобках, то есть 3,122222… = 3,1(2), а 0,0056565656… = 0,00(56). 

С десятичными дробями мы сталкиваемся ежедневно. Когда проходим определенное расстояние, например, 1,8 километров. Или когда покупаем маленькую бутылочку воды: 0,5 литра. Даже когда смотрим прогноз погоды: скорость ветра указывается десятичной дробью, например, 5,6 км/ч. 

Мы разобрались, что такое десятичные дроби и какими они бывают. Теперь разберемся, как перейти от десятичной дроби к обыкновенной и наоборот.

Связь десятичных и обыкновенных дробей 

Представим, что нам дан пример на сложение десятичной и обыкновенной дробей. Решая его, нам придется определиться, в каких дробях производить вычисления. В разных задачах удобно использовать разные виды дробей. Поэтому давайте разберемся, как переводить дроби.

Перевод из десятичной дроби в обыкновенную дробь: 

1. Если целая часть равна нулю, то мы получим обыкновенную дробь в пунктах 3–5.
2. Если целая часть не равна нулю, то мы получим смешанное число, у которого целая часть будет совпадать с целой частью десятичной дроби, а дробную часть мы получим в пунктах 3–5.
3. В числитель дробной части заносим дробную часть десятичной дроби.
4. В знаменатель дробной части вносим десятку в такой степени, сколько цифр после запятой в исходной десятичной дроби.
5. Сокращаем получившуюся дробь при необходимости.

Например, \(0,08=\frac{8}{10^2}=\frac{8}{100}=\frac{2}{25}\). 

Перевод из обыкновенной дроби или смешанного числа в десятичную дробь: 

1. Разделим числитель обыкновенной дроби на ее знаменатель.
2. Если нам нужно перевести смешанное число в десятичную дробь, то сначала мы должны перевести смешанное число в неправильную дробь и потом производить деление числителя на знаменатель. 

Переведем \(\frac{16}{5}\) в десятичную дробь:

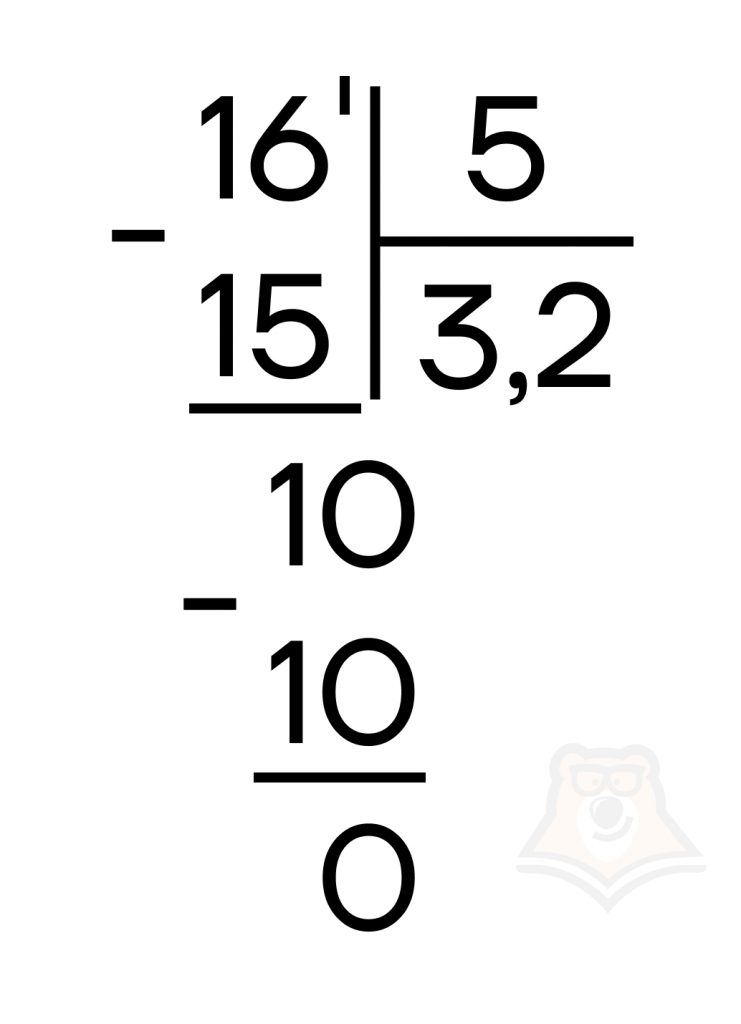
Приведем пример задания №6 из ЕГЭ по профильной математике, где встречаются разные виды дробей вместе.

Задание. Найдите значение выражения: \((\frac{18}{7}-1,2)* 5\frac{5}{6}\).

Решение. \(1,2 = 1\frac{2}{10}=1\frac{1}{5}=\frac{6}{5}\).

Теперь выполним действие в скобках: \(\frac{18}{7}-\frac{6}{5}\):
1. Найдем общий знаменатель: НОК\((7,5) = 35\)
2. Найдем дополнительные множители: для первой дроби – \(35:7= 5\); для второй – \(35:5= 7\).
3. Домножим числитель и знаменатель каждой дроби на ее дополнительный множитель: \(\frac{18*5}{7*5}+\frac{6*7}{5*7}\)
4. Вычтем получившиеся дроби: \(\frac{90}{35}+\frac{42}{35}=\frac{48}{35}\).

Выполним умножение: \(\frac{48}{35}*5\frac{5}{6}=\frac{48}{35}*\frac{6*5+5}{6}=\frac{48}{35}*\frac{35}{6}=\frac{48}{6}=8\)

Ответ: 8

Мы разобрались, как переходить от одного вида дробей к другому, далее посмотрим, как сравнивать между собой десятичные дроби. 

Сравнение десятичных дробей 

Чтобы сравнить десятичные дроби между собой, необходимо привести их к одинаковому количеству цифр после запятой. 

Важно, что к любой конечной дроби можно добавить справа сколько угодно нулей, значение дроби от этого не изменится. То есть \(0,67=0,67000\).

После того как мы сравняли количество цифр после запятой, нужно в первую очередь сравнить целую часть дробей. 

Если у одной дроби целая часть больше, то эта дробь и будет большей и неважно, что стоит в дробной части каждой дроби. Если же целая часть дробей равна, мы должны сравнить дробную часть, у какой дроби она меньше, та дробь и будет меньше. 

Рассмотрим пример: необходимо сравнить дроби \(0,67\) и \(0,125\).

Допишем к первой дроби слева 0, чтобы уравнять количество знаков после запятой, теперь мы сравниваем дроби \(0,670\) и \(0,125\). Целая часть у этих дробей одинаковая: 0. Сравним дробные части: \(670>125\), следовательно, \(0,67>0,125\).

Почему десятичные дроби так важны на спортивных соревнованиях? В современном мире никакое крупное состязание по плаванию или легкой атлетике не обходится без очень точного секундомера и фотофиниша. Сейчас спортсменов от призовых мест отделяют сотые доли секунд. Например, на Чемпионате мира по легкой атлетике в 2022 году судьбу золотой медали на дистанции 60 метров среди женщин решили 0,03 секунды, именно такая разница во времени разделила первое и второе место.

Арифметические действия с десятичными дробями

Десятичные дроби можно не только сравнивать: также, как и обычные дроби, с ними можно выполнять различные действия. Давайте разберемся, как их складывать, вычитать, умножать и делить. 

Сложение и вычитание десятичных дробей

При сложении (вычитании) десятичных дробей необходимо изначально уравнять количество знаков после запятой, дописав к одной из дробей нули справа при необходимости. 

Далее записываем одну дробь под другую так, чтобы запятые дробей оказались на одном уровне. Затем, не обращая внимания на запятые, выполняется сложение (вычитание), так же как и с обычными числами. Последнее действие – поставить запятую в получившемся числе так, чтобы она оказалась на одном уровне с запятыми исходных дробей. 

Вычислим: \(0,45+0,567 = 0,450 + 0,567\).

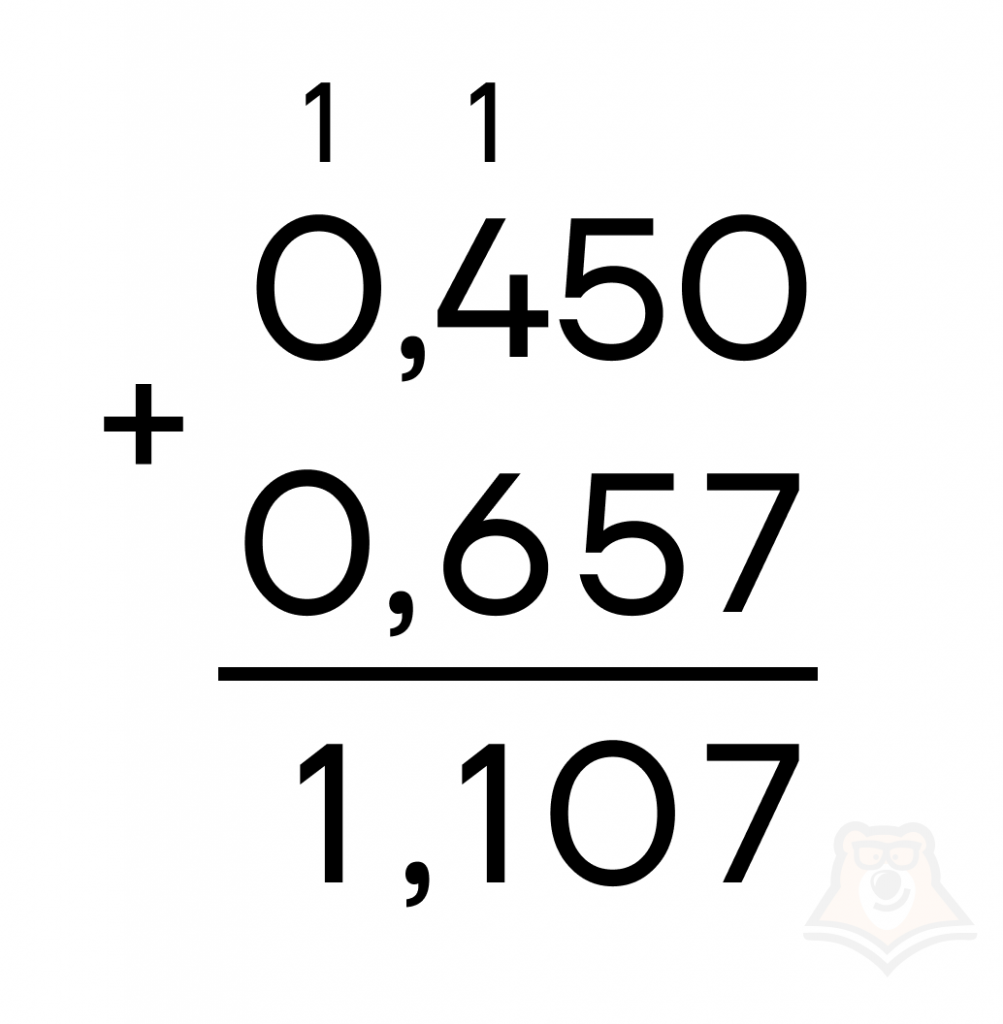
Умножение и деление десятичной дроби на 10, 100, 1000 и так далее

Когда мы умножаем десятичную дробь на десять в какой-то степени, мы переносим запятую вправо на количество цифр, равное степени десяти. 

То есть, умножая \(0,1673\) на \(100\) мы получим \(16,73\).

Аналогично с делением, разница только в том, что запятая перемещается влево. 

Разделим \(0,045\) на \(1000\) и получим \(0,000045\).

Умножение десятичных дробей

При умножении десятичных дробей мы должны действовать так же как и при умножении натуральных чисел. Записываем одну дробь под другой и умножаем в столбик, не обращая внимания на запятые. Затем в полученном после умножения числе отделяем запятой справа столько цифр, сколько суммарно цифр после запятой в исходных дробях. 

Умножим \(0,56\) на \(0,7\). В ответе мы должны отделить справа три цифры запятой, так как в первой дроби после запятой две цифры, во второй – одна, а два плюс один равно три. 

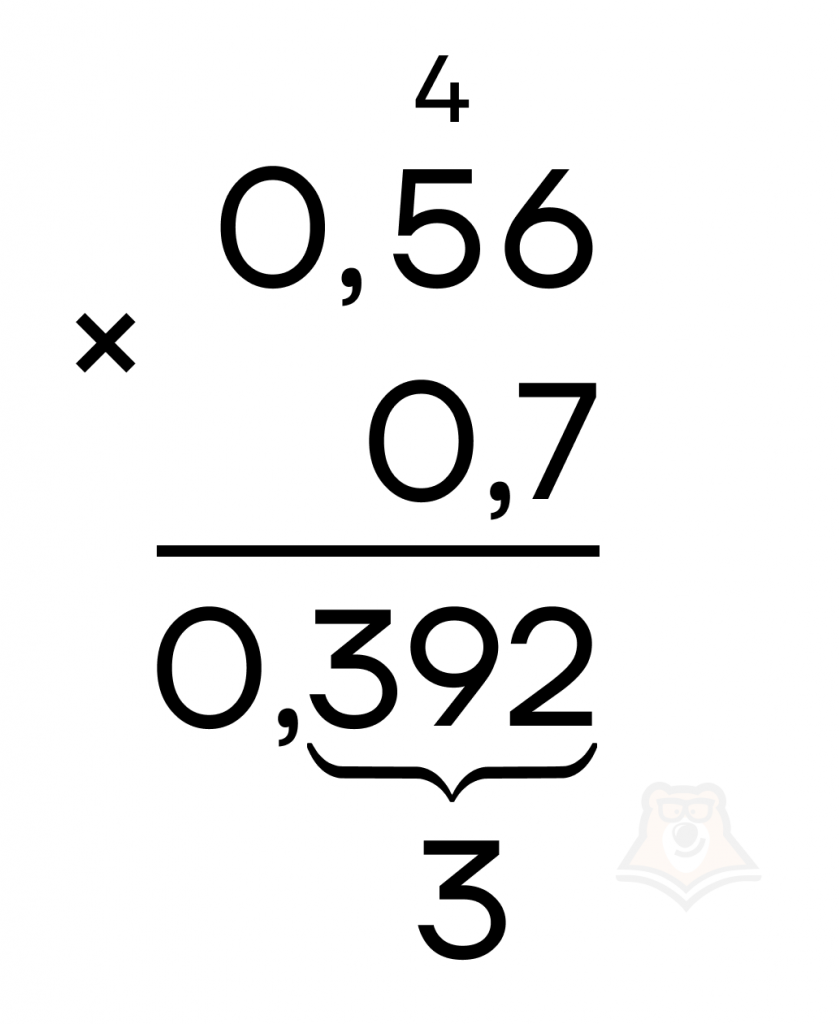
Деление десятичной дроби на целое число 

При делении десятичной дроби на целое число мы совершаем деление в столбик также как делали бы и с целыми числами. Единственное отличие в том, что когда заканчивается деление целой части, мы должны поставить запятую в частном. То есть, перед тем как сносить первую цифру из дробной части, в получившемся ответе надо поставить запятую. 

Например, \(5,32:4\)

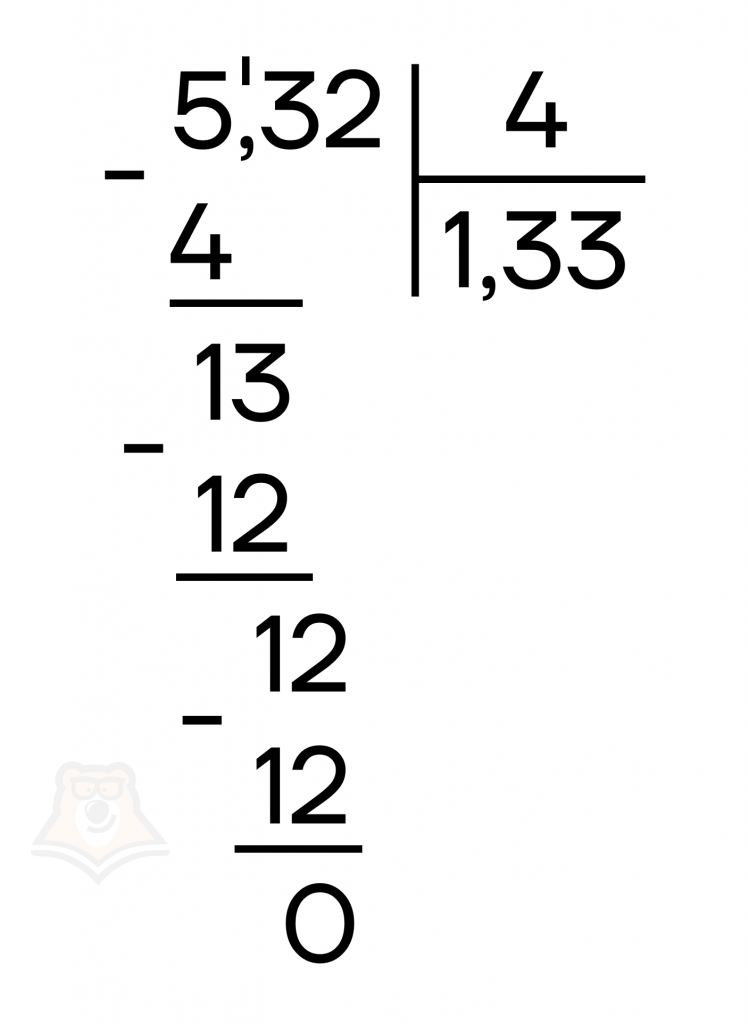
Деление десятичных дробей

Важно запомнить, что делить на десятичную дробь нельзя! Но как тогда производить деление? 

Поскольку мы не можем разделить число на дробь, то нужно дробь преобразовать в целое число! Как это сделать? Мы уже разбирали, что если умножить десятичную дробь на \(10, 100, 1000\) и так далее, то мы переносим запятую вправо, то есть увеличиваем число. Например, \(0,167*1000=167\). Следовательно, мы можем преобразовать делитель, если перенесем запятую вправо на нужное количество знаков.

Но тогда мы обязательно должны умножить и делимое, чтобы значение выражения не поменялось. 

Представим, что нам нужно разделить \(200\) на \(2\), но мы решили умножить делитель на 10. Тогда получим: \(\frac{200}{2*10}=\frac{200}{20}=10\), хотя должны были получить \(100\). Но если бы мы умножили и \(200\) на \(10\), то ответ бы не поменялся: \(\frac{200*10}{2*10}=100\). 

На самом деле, мы тут используем основное свойство дроби, которое применимо и для десятичных дробей. То есть мы умножаем оба числа на одну и ту же величину, благодаря чему не меняется результат деления. 

После этого мы уже можем делить либо дробь на целое число, либо два целых числа друг на друга.

Рассмотрим пример: \(0,186:0,12=18,6:12\)

Умножили делимое и делитель на 100, чтобы делитель стал целым числом. Теперь воспользуемся предыдущим пунктом и произведем деление.

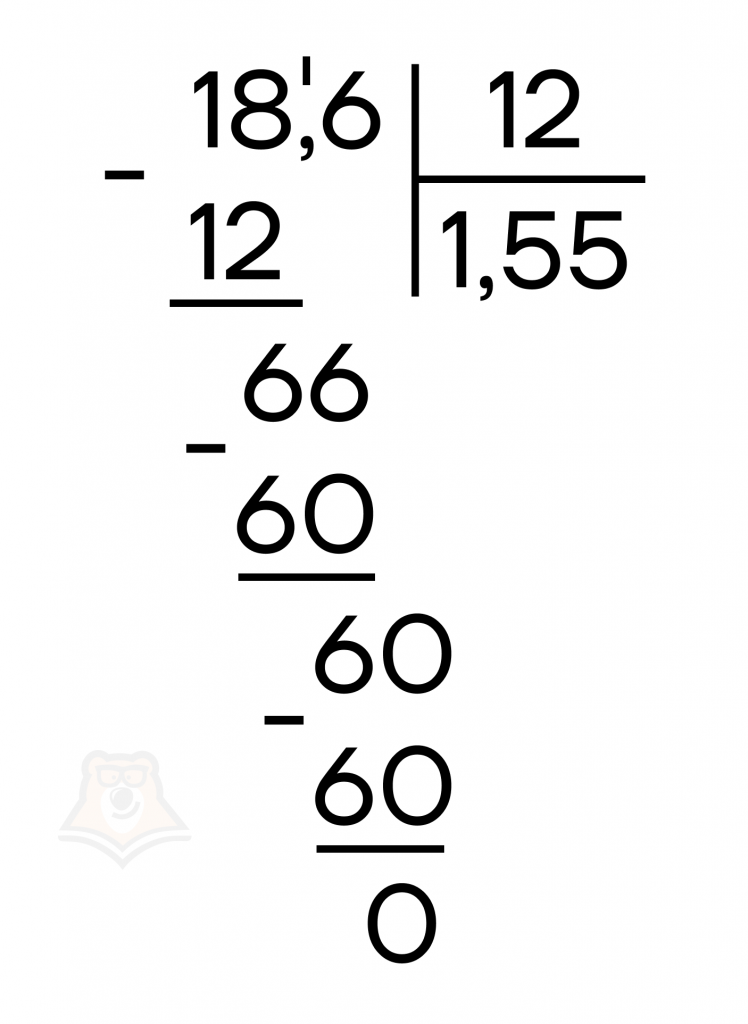
При делении дроби на дробь или на целое число мы можем получить бесконечную дробь, тогда нужно просто остановить деление, дойдя до нужного числа после запятой.

Десятичные дроби могут встретиться в ОГЭ по математике в задании № 6.

Задание. Найдите значение выражения: \(\frac{4,8*0,4}{0,6}\).

Решение. Для решения воспользуемся счетом в столбик. Сначала найдем значение выражения в числителе, а после разделим числитель на знаменатель.

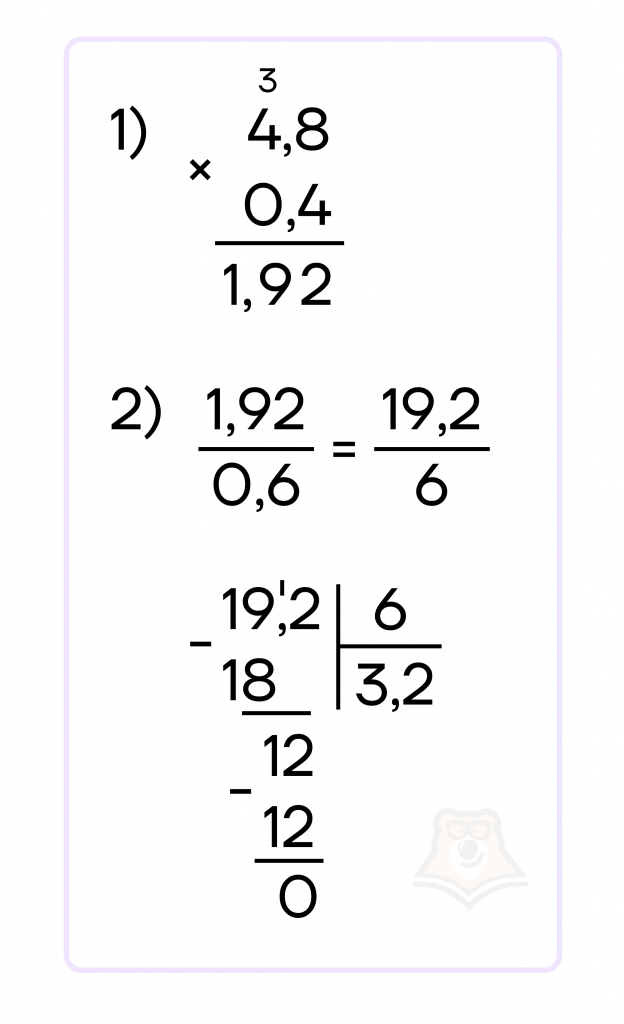
Ответ: 3,2

В данной статье мы познакомились с различными дробями, научились решать примеры с ними, а также узнали, как сравнивать десятичные дроби между собой. А для продолжения изучения такой прекрасной науки, как математика, мы предлагаем вам ознакомиться с нашей следующей статьей «Одночлены и действия с ними». 

Термины

Натуральные числа – числа, возникающие естественным образом при счете (1, 2, 3, 4, 5, 6, 7 и так далее).

Фактчек

• Дроби бывают двух видов: обыкновенные (записываются с помощью дробной черты) и десятичные ( записываются в строчку, целая часть от дробной отделяется запятой). 
• Основное свойство дроби: при одновременном умножении числителя и знаменателя дроби на число, неравное нулю, значение самой дроби не изменится.
• Для того чтобы сложить или вычесть обыкновенные дроби, необходимо сначала привести их к общему знаменателю, если изначально их знаменатели разные. 
• Если мы складываем смешанные числа, их нужно предварительно перевести в неправильную дробь.
• При умножении обыкновенных дробей мы должны перемножить числители и знаменатели и затем сократить получившуюся дробь, если это необходимо.
• При сложении, вычитании и умножении десятичных дробей мы действуем так же как и с целыми числами, и только в конце дописываем запятую. 

Проверь себя

Задание 1.
Чему равна сумма двух дробей \(\frac{4}{5}+\frac{7}{10}\)?

1. \(\frac{11}{15}\)
2. \(\frac{14}{25}\)
3. \(1\frac{1}{2}\)
4. \(1\frac{1}{5}\)

Задание 2.
Чему равно произведение двух дробей \(\frac{3}{7}*\frac{4}{9}\)?

1. \(\frac{4}{21}\)
2. \(\frac{7}{16}\)
3. \(\frac{55}{63}\)
4. \(1\frac{4}{5}\)

Задание 3.
Какой знак нужно поставить при сравнении двух дробей \(0,034\) и \(0,5\)?

1. \(>\)
2. \(<\)
3. \(=\)
4. Эти дроби нельзя сравнивать, так как они имеют разное количество знаков после запятой. 

Задание 4.
Чему равно произведение двух десятичных дробей \(0,45* 0,3\)?

1. \(0,0135\)
2. \(1,35\)
3. \(13,5\)
4. \(0,135\)

Задание 5.
Чему равно частное двух дробей \(2,48*1,6\)?

1. \(1,55\)
2. \(1,2\)
3. \(3,45\)
4. \(0,56\)

Ответы: 1. — 3 2. — 1 3. — 2 4. — 4 5.— 1