Неравенства с параметрами

На этой странице вы узнаете

• Должен ли ответ быть красивым числом?
• Когда появились примеры с параметрами?
• Парабола: как она поможет вам на ЕГЭ?

Предпоследнее задание в ЕГЭ по профильной математике. Возможно, самое сложное. Но так ли оно пугающе, как о нем говорят? Узнаем об этом в этой статье!

Линейные неравенства и неравенства, приводимые к линейным с параметром

Итак, будем изучать эту тему сразу же на примерах, потому что теории тут не так много. Успешное решение параметров зависит от количества разобранных примеров: чем больше, тем лучше! Поскольку в параметрах невозможно выделить алгоритм, который будет подходить ко всем условиям, то тут все зависит от логических рассуждений. Именно поэтому чем больше решено примеров, тем лучше, хотя бы потому, что решать знакомые задачи намного проще. 

Напомним, что решить неравенство с параметром — найти все значения x при определенных значениях параметра a.

Рассматриваем все случаи относительно коэффициентов при x.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №18. 

Задание. Решить неравенство \(\frac{x(a-2)}{a-1}-\frac{3a}{4}\leq 2x-a\) при \(а ≠ 1\). 

Решение. Проведем некоторые преобразования над неравенством. Перенесем \(2x\) в левую часть, а \(\frac{3a}{4}\) — в правую:

\(\frac{x(a-2)}{a-1}-2x\leq \frac{3a}{4}-a\)

Приведем к общему знаменателю:

\(\frac{ax-2x-2ax+2x}{a-1}\leq -\frac{a}{4}\)

Проведем подсчеты в левой части:

\(-\frac{ax}{a-1}\leq -\frac{a}{4}\)

Домножим на \(-1\). При этом знак неравенства меняется на противоположный:

\(\frac{a}{a-1}x\geq \frac{a}{4}\)

Оставим x в левой части, а все остальное перенесем в правую:

\(x\geq \frac{a(a-1)}{4a}\)
\(x\geq \frac{a-1}{4}\)

Рассмотрим все возможные случаи для a:

1) Если \(\frac{a}{a-1}>0\) или \(a\in (-\infty; 0)\cup (1;+\infty)\), тогда \(x\geq \frac{a-1}{4}\). Проверим это на примере. Допустим, \(a=2\), тогда:

\(\frac{2}{2-1}x\geq \frac{2}{4}\)
\(2x\geq \frac{1}{2}\)
\(2x\geq \frac{1}{2}\)
\(x\geq \frac{1}{4}\)

То же самое получим, если подставим \(a=2\) в \(x\geq \frac{a-1}{4}\):

\(x\geq \frac{2-1}{4}\)
\(x\geq \frac{1}{4}\)

Соответственно, неравенство выполняется. Аналогично можно проверить и остальные случаи.

2) Если \(\frac{a}{a-1}=0\) или \(a=0\), тогда x — любое действительное число.
3) Если \(\frac{a}{a-1}<0\) или \(a\in (0; 1)\), тогда \(x\leq \frac{a-1}{4}\). 

Ответ. \(x\in [\frac{a-1}{4}; +\infty]\) при \(a\in (-\infty; 0)\cup (1; +\infty); x\in R\) при \(a = 0; x\in [-\infty; \frac{a-1}{4}]\) при \(a\in (0; 1)\).

Как вы можете заметить, такие задачи решаются легко, но важно не забыть рассмотреть все возможные случаи! Посмотрим на неравенство с параметром, которое сводится к линейному.

Пример 1. Решить неравенство \((a-2)x > a^2-4\) для любого значения параметра a. 

Рассмотрим случай, когда \(a = 2\). В этом случае в левой части будет \(0 * x\), а в правой — 0, и получим:

\(0*x>0\)

При таком значении a у x нет решений.

Если же \(a > 2\), тогда оставим x в левой части, все остальное перенесем в правую и получим:

\(x >\frac{a^2-4}{a-2}\). Преобразуем с помощью формулы разности квадратов \(a^2-b^2=(a-b)(a+b)\): 

\(x >\frac{(a-2)(a+2)}{a-2}\)

И в числителе, и в знаменателе у нас есть \((a-2)\), значит, можем сократить:

\(x > a+2\)

При \(a < 2\) будет то же самое, но знак неравенства меняется, так как мы делим на отрицательную величину:

\(x <\frac{a^2-4}{a-2}\) или \(x < a+2\).

Ответ: \(x\notin R\) при \(a=2; x > a+2\) при \(a > 2; x < a+2\) при \(a < 2\).

С линейными неравенствами разобрались, здесь все очень легко. Переходим к квадратичным неравенствам.

Квадратичные неравенства с параметром

Они практически не отличаются от линейных, только теперь мы будем использовать дискриминант и параболу для анализа. Давайте разберемся, как это делать.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №18. 

Задание. Решить неравенство \(ax^2-8x-16>0\) при всех значениях параметра а.

Решение. Заметим, что при \(a = 0\) наше неравенство превращается в линейное:

\(-8x-16>0\)
\(x< -2\)

Если же \(a\neq 0\), то неравенство становится квадратным. Посчитаем дискриминант:

\(D = 64+64a=64(1+a)\)

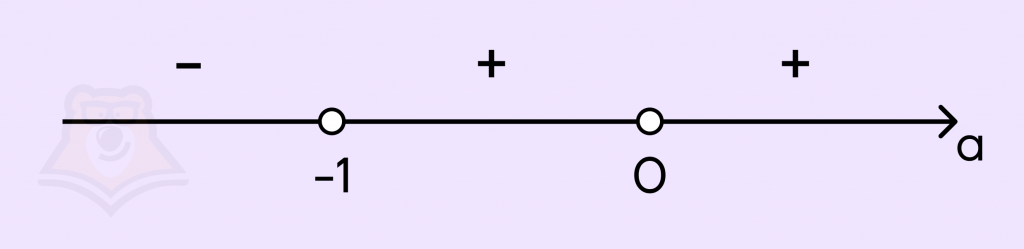
Имеем: при \(a<-1\) дискриминант \(D<0; D=0\) при \(a=-1\); при \(a>-1\) дискриминант \(D>0\).

Найдем корни:
\(x_1=\frac{8+\sqrt{64(1+a)}}{2a}\)
\(x_2=\frac{4+\sqrt{64(1-a)}}{2a}\)

\(x_1=\frac{8+8\sqrt{1+a}}{2a}\)
\(x_2=\frac{8+8\sqrt{64(1-a)}}{2a}\)

\(x_1=\frac{4+4\sqrt{1+a}}{a}\)
\(x_2=\frac{4+4\sqrt{64(1-a)}}{a}\)

Рассмотрим все случаи:

1) \(a < -1; D < 0\).

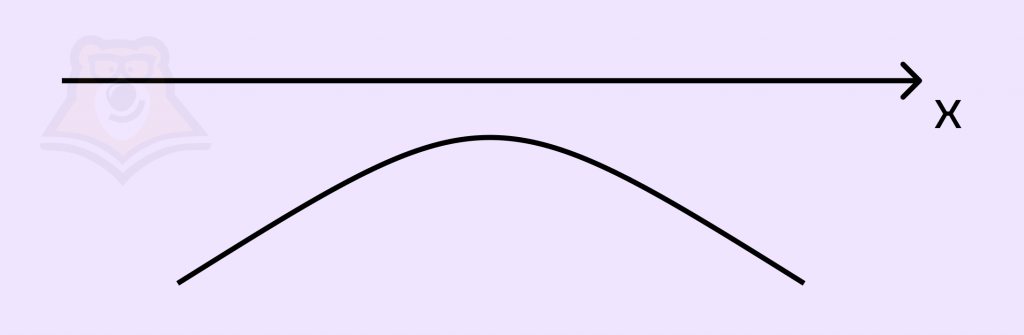
Парабола не пересекает ось x, и это значит, что решений нет. Подробнее про параболу и влиянии коэффициентов на ее вид можете узнать в статье «Основные элементарные функции».

2) \(a = -1; D = 0\).

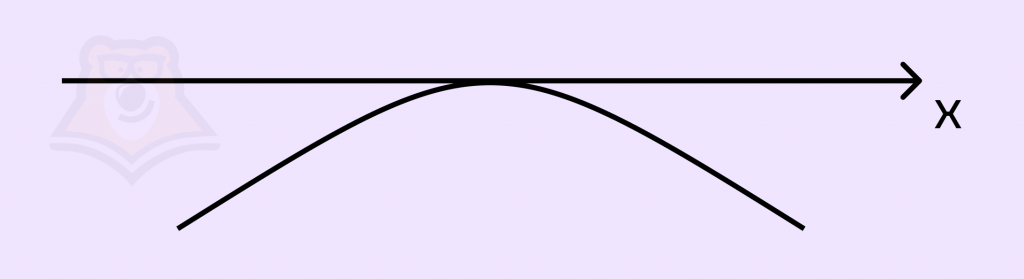
Только вершина касается оси \(x\), но по условию задачи равенство \(0\) не подходит.

3) \(-1 < a < 0, D > 0\). В этом случае ветви параболы направлены вниз, значит:

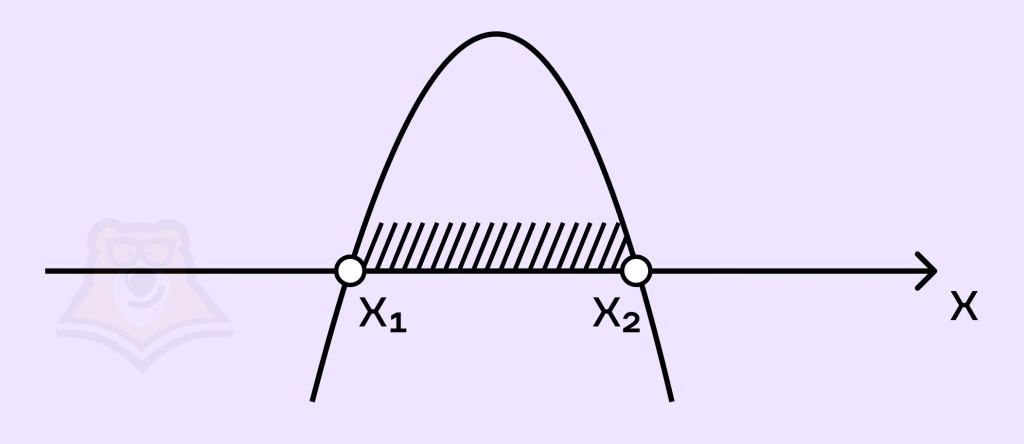
Многочлен положителен при:

\(x\in (\frac{4+4\sqrt{1+a}}{a}; \frac{4-4\sqrt{1+a}}{a})\)

Здесь важно отметить, что \(\frac{4+4\sqrt{1+a}}{a}\) меньше, так как a отрицательно, поэтому его и написали первым.

4) \(a > 0; D > 0\).В этом случае ветви параболы направлены вверх. Найдем корни:

\(x_{1,2}=\frac{8\pm 8\sqrt{1+a}}{2a}=\frac{4\pm 4\sqrt{1+a}}{a}\)

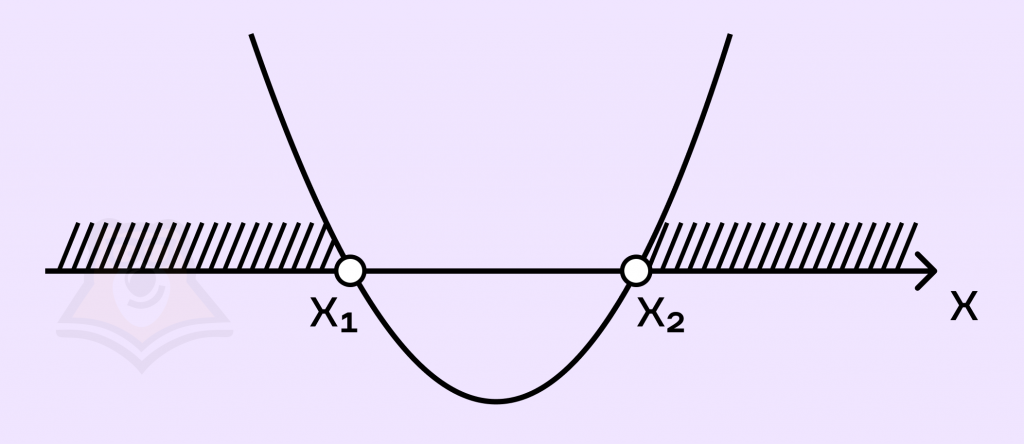
Соответственно, многочлен будет положительный при таком условии:

\(x\in (-\infty; \frac{4-4\sqrt{1+a}}{a})\cup (\frac{4+4\sqrt{1+a}}{a};+\infty)\)

Мы рассмотрели все возможные случаи и можем написать ответ.

Ответ: \(x< -1\) при \(a = 0; x\notin R\) при \(a\leq -1; x\in (\frac{4+4\sqrt{1+a}}{a}; \frac{4-4\sqrt{1+a}}{a})\) при \(-1 < a < 0; x\in (-\infty; \frac{4-4\sqrt{1+a}}{a})\cup (\frac{4+4\sqrt{1+a}}{a};+\infty)\) при \(a > 0\).

Должен ли быть ответ быть красивым числом? Как вы могли заметить, решения с корнями и другими страшными математическими вещами в таких задачах вполне возможны, поэтому не удивляйтесь на экзамене, если посчитаете что-то подобное. Главное перепроверяйте, чтобы все точно было решено верно.

Ну а мы идем дальше, к иррациональным неравенствам с параметром!

Иррациональные неравенства с параметром

Сейчас мы заметим, что практически ничего нового эти неравенства нам не дают. Рассмотрим на примере.

Пример 2. Решите неравенство \(5(2a+x)+9a\sqrt{2a+x}>-2a^2\) для любого значения a.

Решение. Сначала перенесем все в левую часть: 

\(5(2a+x)+9a\sqrt{2a+x}-2a^2>0\)

Что мы можем увидеть в левой части неравенства? Правильно, квадратный трехчлен относительно \(\sqrt{2a+x}\). Заменим \(\sqrt{2a+x}\) на \(t\), тогда:

\(5t^2+9at-2a^2>0\)
\(D = 81a^2+40a^2\)
\(t_{1,2}=\frac{-9a\pm \sqrt{81a^2+40a^2}}{10}=\frac{-9a\pm 11a}{10}\)
\(t_1=\frac{-9a+11a}{10}\)
\(t_2=\frac{-9a-11a}{10}\)
\(t_1=\frac{2a}{10}\)
\(t_2=\frac{-20a}{10}\)
\(t_1=\frac{a}{5}\)
\(t_2=-2a\)

Разложим левую часть с помощью формулы разложения квадратного трехчлена на множители:

\(5(\sqrt{x+2a}+2a)(\sqrt{x+2a}-\frac{a}{5})>0\)

Рассмотрим случай, когда \(a = 0\):

\(5\sqrt{x}*\sqrt{x}>0\)
\(x>0\)

Помимо этого, при \(a < 0\) значение во второй скобке \((\sqrt{x+2a}-a5)\) больше нуля. Значит можно неравенство в таком случае переписать следующим образом:

\(\sqrt{x+2a}+2a > 0\)
\(\sqrt{x+2a} > -2a\)
\(x+2a > 4a^2\)
\(x>4a^2-2a\)

При \(а > 0\) в первой скобке \((\sqrt{x+2a}+2a)\) значение будет положительным, значит перепишем неравенство так:

\(\sqrt{x+2a}-\frac{a}{5}>0\)
\(\sqrt{x+2a}>\frac{a}{5}\)
\(x+2a>\frac{a^2}{25}\)
\(x>\frac{a^2}{25}-2a\)

Это практически все задание, осталось только последнее: \(a = 0\) входит в последний случай, соответственно знаем ответ.

Ответ: при \(a\geq 0\), то \(x>\frac{a^2}{25}-2a\); при \(a < 0\), то \(x>4a^2-2a\). 

Когда появились примеры с параметрами? Задачи на уравнения с параметром встречались уже в астрономическом трактате«Ариабхаттиам», который был составлен в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта, в 7 веке изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме с параметром: \(ax^2+bx=c , a>0\).

Супер, корни прошли, теперь на подходе логарифмы!

Уравнения и неравенства с параметрами, содержащие логарифмы

Сначала решим такое уравнение: \(log_4(16^x+a)=x\). Нужно найти все значения параметра a, при котором это уравнение будет иметь одно или два решения.

Вспомним, что логарифм, если простыми словами, — это показатель степени. Подробнее о логарифмах вы можете прочесть в статье «Логарифмические уравнения и неравенства». То есть мы можем преобразовать наше уравнение с помощью определения логарифма в другое, попроще:

\(16^x+a=4^x\)
\(16^x-4^x+a=0\)
\(4^{2x}-4^x+a=0\)

Пусть \(t=4^x, t > 0\), тогда:

\(t^2-t+a=0\)

Это квадратное уравнение. Чтобы оно имело один или два корня, нужно, чтобы дискриминант был больше или равен \(0\):

\(D = 1-4a\geq 0\)
\(a\leq \frac{1}{4}\)

Ответ: \(a\leq \frac{1}{4}\)

Неравенства решаются примерно так же. 

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №18. 

Задание. Найти все значения параметра \(b\), при которых \(x=14\) является решением неравенства \((x-14)(x-26)\sqrt{b^2-24blog_{13}(x-13)-25}\geq 0\), а число \(x=26\) не является.

Решение. Неравенство равносильно системе:

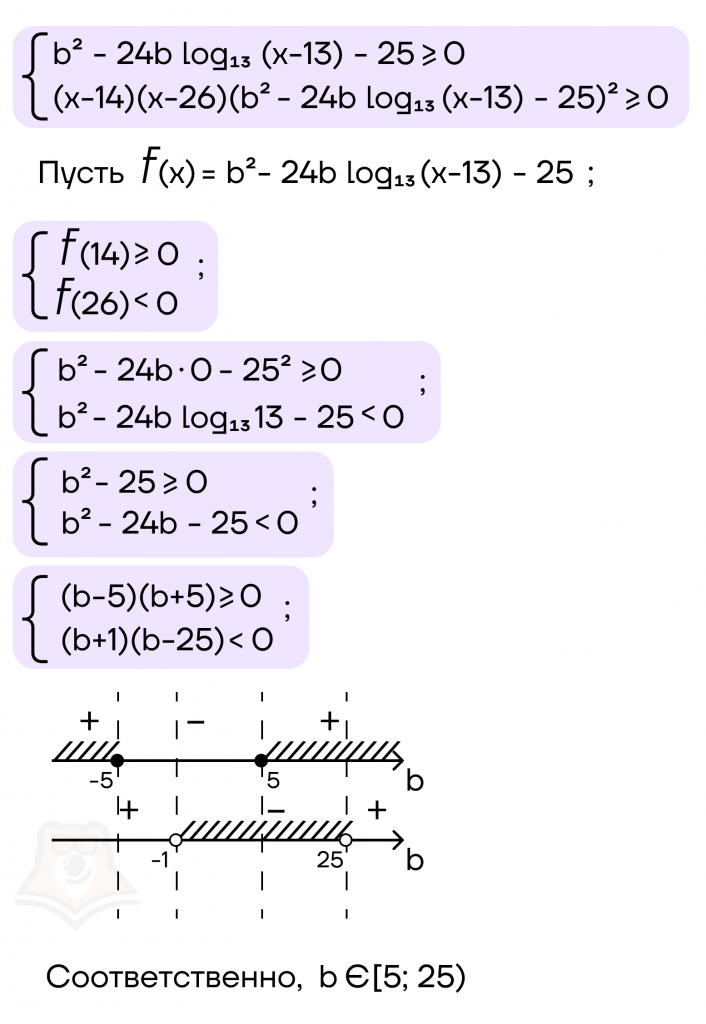
Ответ. \(b\in [5;25)\)

Идем дальше, к задачам с требованием выполнения или невыполнения неравенства для всех значений параметра.

Задачи с требованием выполнения (или невыполнения) неравенства для всех значений параметра

Подобные задачи мы сегодня уже решали. Например, в разделе про логарифмы. Сразу рассмотрим две последние задачи на сегодня и разберемся, как решать такие неравенства.

Пример 3. Решите неравенство \(4ax+5cos(\frac{\pi}{3})\geq 0\) при всех значениях параметра a.

В условии значение косинуса табличное, а значит он равен \(\frac{1}{2}\). Перенесем все числа в правую часть:

\(ax\geq -\frac{5}{8}\)

Теперь рассмотрим три потенциальных случая:

1. \(a = 0\), в таком случае неравенство будет выглядеть так:

\(0\geq -\frac{5}{8}\)

Это выполняется при любых значениях x.

2. \(a < 0\), тогда при делении обеих частей неравенства на a знак \(\geq\) изменится на \(\leq\). Получим:

\(x\leq -\frac{5}{8a}\)

3. \(a > 0\). Поделим обе части неравенства на а и получим:

\(x\geq -\frac{5}{8a}\)

Ответ: \(x\in R\) при \(a = 0; x\leq -\frac{5}{8a}\) при \(a < 0; x\geq -\frac{5}{8a}\) при \(a > 0\).

Да, это была правда легкая задачка. Теперь решим что-нибудь посложнее.

Пример 4. Решите неравенство \(b(x^2-6)\geq (2-3b^2)x\) при всех значениях параметра b. 

Сначала преобразуем неравенство вот так:

\(bx^2-6b-(2-3b^2)x\geq 0\)
\(bx^2+(3b^2-2)x-6b\geq 0\)

Что-то подобное мы сегодня уже решали. Сначала рассмотрим случай, когда \(b\neq 0\):

\(-2x\geq 0\)
\(x\leq 0\)

Теперь остановимся на случае, когда \(b0\). В таком случае неравенство станет квадратичным. Дискриминант:

\(D = 9b^4-12b^2+24b^2=(3b^2+2)^2\)

Дискриминант больше нуля, так как он в квадрате. Значит, что уравнение \(bx^2+(3b^2-2)x-6b=0\) всегда имеет два корня:

\(x_1=-3b\)
\(x_2=\frac{2}{b}\)

Расписать квадратичное неравенство найденными корнями можно так:

\(a(x-x_1)(x-x_2)\)

Тогда получаем:

\((bx-2)(x+3b)\geq 0\)

Если b меньше нуля, то есть \(b < 0\), тогда \(x_1>x_2\) и ветви у параболы \(y=(bx-2)(x+3b)\geq 0\) направлены вниз:

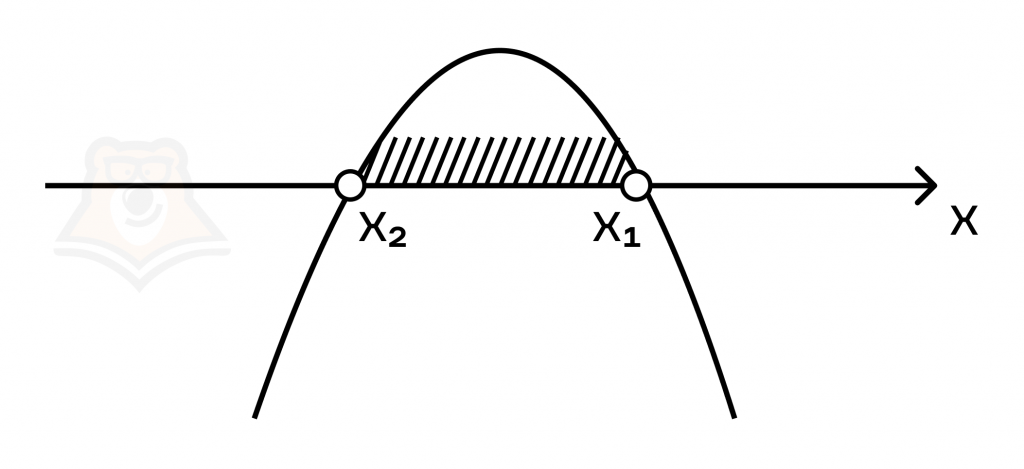
Следовательно, решением будет \(x\in [\frac{2}{b};-3b]\)

Если же \(b > 0\), тогда \(x_1<x_2\) и ветви у параболы \(y=(bx-2)(x+3b)\geq 0\) направлены вверх:

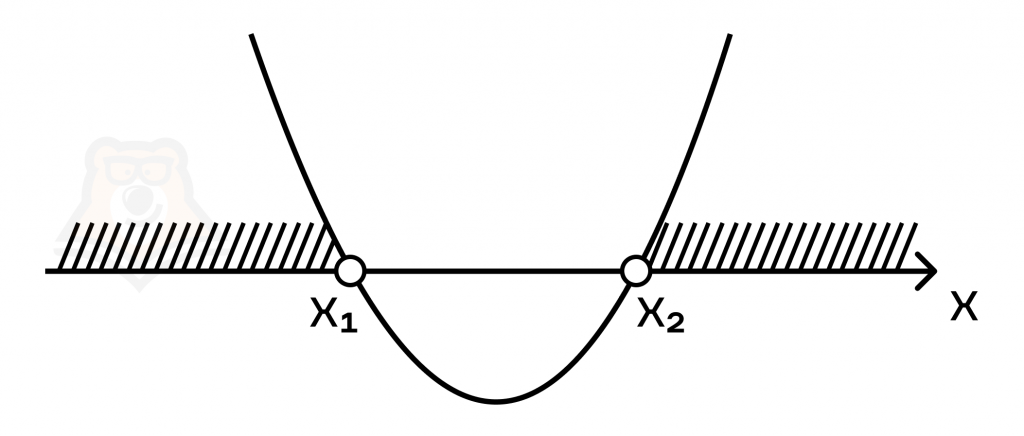
А это значит, что решение: \(x\in (-\infty; -3b]\cup [\frac{2}{b};+\infty)\). 

Ответ: \(x\leq 0\) при \(b=0; x\in (-\infty; -3b]\cup [\frac{2}{b};+\infty)\) при \(b>0; x\in [\frac{2}{b};-3a]\) при \(b<0\).

Парабола: как она поможет вам на ЕГЭ? Сегодня мы видели два неравенства с параметрами, в решении которых нам очень помогла парабола. У нее есть такие свойства, которые помогают решать квадратичные уравнения и неравенства с параметрами.

На этом наше изучение неравенств с параметрами окончено. Теперь вы знаете, как решать их, чтобы получить за них максимальный балл на ЕГЭ по профильной математике! А чтобы получать максимальный балл за другие задания, можете прочитать статью «Текстовые задачи».

Термины

Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле \(D=b^2-4ac\), где а, b и с берутся из уравнения.

Парабола — это незамкнутая линия, точки на которой равноудалены от оси симметрии.

Фактчек

• В неравенствах с параметром важно рассмотреть все возможные значения параметра a.
• В квадратичных неравенствах с параметром для анализа используем параболу.
• Ответы с корнями — нормальное явление для этого задания.

Проверь себя

Задание 1.
Что значит «Решить неравенство с параметром»?

1. Найти ОДЗ параметра а.
2. Определить, при каких x существует параметр a.
3. Найти все значения параметра a при определенных значениях x.
4. Найти все значения x при определенных значениях параметра a.

Задание 2.
При каких значениях параметра а ветви параболы будут направлены вниз у неравенства \(ax^2-4x-20>0\)?

1. \(a > 0\)
2. \(a = 1\)
3. \(a < 0\)
4. \(a = 0\)

Задание 3.
Как решить данное неравенство: \(10(4a-x)+15a\sqrt{4a-x}-5a>0\)?

1. Как линейное неравенство.
2. С помощью замены \(t = 4a\).
3. Как квадратный трехчлен.
4. Рассмотреть все случаи, когда корень отрицателен.

Задание 4.

Какие значения принимает x при \(a = 0\) в данном неравенстве: \(ax < -1\)?

1. \(x\notin R\).
2. \(x\in R\).
3. \(x > 0\).
4. \(x = 0\).

Ответы: 1. — 4; 2. — 3; 3. — 3; 4. — 1.