Подобные фигуры и тела

На этой странице вы узнаете

• Где мы можем встретить темы по геометрии в реальном мире?
• Почему в геометрии не используют слово «похожи»?
• Как быстро запомнить отношения подобных тел?

Подобные тела встречаются в жизни намного чаще, чем кажется на первый взгляд. Давайте систематизируем знания на данную тему и научимся применять их при решении задач на практике. 

Подобные фигуры

В математике концепция подобных тел и фигур играет важную роль в изучении геометрии и пропорций.

Представьте, что у вас есть картинка на телефоне. Когда вы увеличиваете размер этой картинки в своем экране, скажем, в два раза, длина каждой стороны этого изображения также увеличится вдвое, при этом сохранится форма и пропорции начальной картинки. Это пример масштабирования, при котором сама форма изображения остается неизменной, меняется только его размер.  

Для того, чтобы перейти к рассмотрению подобных тел в пространстве, вспомним ранее приобретенные знания.

Масштабирование картинки на телефоне – яркий пример подобия фигур на плоскости. Какие знания при работе с геометрическими фигурами пригодятся нам в этой теме? Давайте поэтапно разбираться с поставленными вопросами. 

Для это нужно вспоминать теорию, ведь без нее нам не разобраться в теме.

• Две фигуры называются равными, если их можно совместить наложением.
• Два тела называются подобными, если одно из них может быть получено путем увеличения или уменьшения всех его линейных размеров в одном и том же отношении.
• Линейные размеры это: длина, ширина, высота, величина диаметра, радиуса, дуги.

Останавливаться на всех фигурах мы не будем, но для примера решим задачу на подобие треугольников Узнать подробнее про него вы можете в статье «Равенство и подобие треугольников». 

Задачи на подобие треугольников встречаются в номере 1 в ЕГЭ по профильной математике.

Задание. Углы А  и В треугольника АВС равны углам А₁ и В₁  треугольника А₁В₁С₁ соответственно. Известно, что \(AB=9, BC=10, AC=11, P_{A1B1C1}=10\). Найдите наименьшую по длине сторону треугольника А₁В₁С₁.

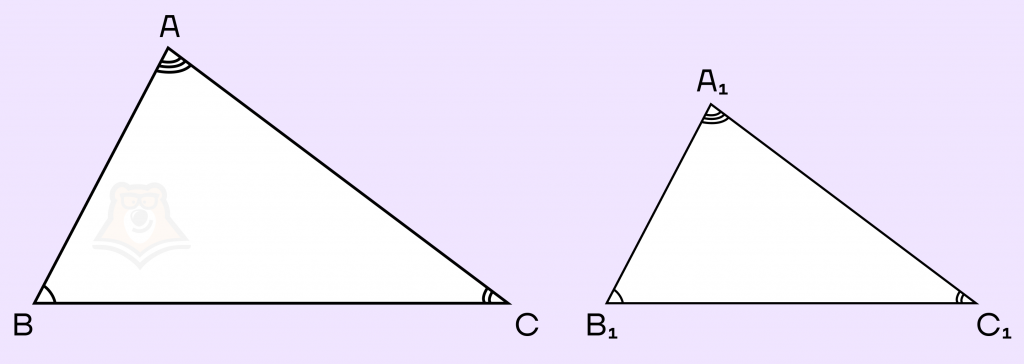
Решение. Вспомним свойства подобия треугольников. Из них следует, что треугольники подобны по двум углам, тогда можем воспользоваться формулой: 

\(\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}=\frac{Р_{АВС}}{Р{А_1В_1С_1}}\)

Из этой формулы следует: \(\frac{10+9+11}{10}=3=k\)

\(k=3\) нам говорит о том, что все стороны относятся как 1 к 3.

Давайте найдем стороны:

\(\frac{1}{3}AB=A_1B_1=\frac{9}{3}=3\)
\(\frac{1}{3}CB=C_1B_1=\frac{10}{3}\)
\(\frac{1}{3}AC=A_1C_1=\frac{11}{3}\)

Тогда наименьшая по длине сторона треугольника А₁В₁С₁, будет сторона А₁В₁ равная 3.

Ответ: 3

Где мы можем встретить темы по геометрии в реальном мире? Темы геометрии применяются в реальном мире в различных областях. Например, в архитектуре геометрия используется для проектирования и строительства зданий, мостов и других сооружений. Также геометрические принципы применяются в дизайне, искусстве, в инженерии и технологиях. Примеры подобных тел в жизни: — чайная ложка и столовая ложка; — машина и игрушечная модель машины; — матрешки Каждый из них демонстрирует концепцию подобия фигур. Например, чайная ложка и столовая ложка имеют схожую форму, но отличаются размером в соответствии с определенным коэффициентом подобия (о нем мы поговорим далее). Аналогично, машина и игрушечная модель машины представляют подобные тела с измененными масштабами.  Рассмотрение подобных тел в реальной жизни помогает увидеть практическое применение геометрии и визуализировать подобие! Что мы сейчас и сделали.

Когда мы рассмотрели основные вопросы, касающиеся подобных фигур на плоскости, то можем перейти к более детальному погружению в тему.

Отношение объемов подобных тел

Главная величина геометрических тел – это их объем. Объем геометрических тел – это величина, которая описывает занимающую этим телом часть пространства или это  положительная величина той части пространства, которую занимает геометрическое тело. 

Если мы имеем дело с равными телами, то можно сделать вывод, что объемы равных тел равны.

Однако с подобием все обстоит несколько иначе. Условно подобность тел можно разделить на две темы: подобность многогранников и подобность цилиндров с конусами. Рассмотрим каждую тему отдельно!

Подобность многогранников

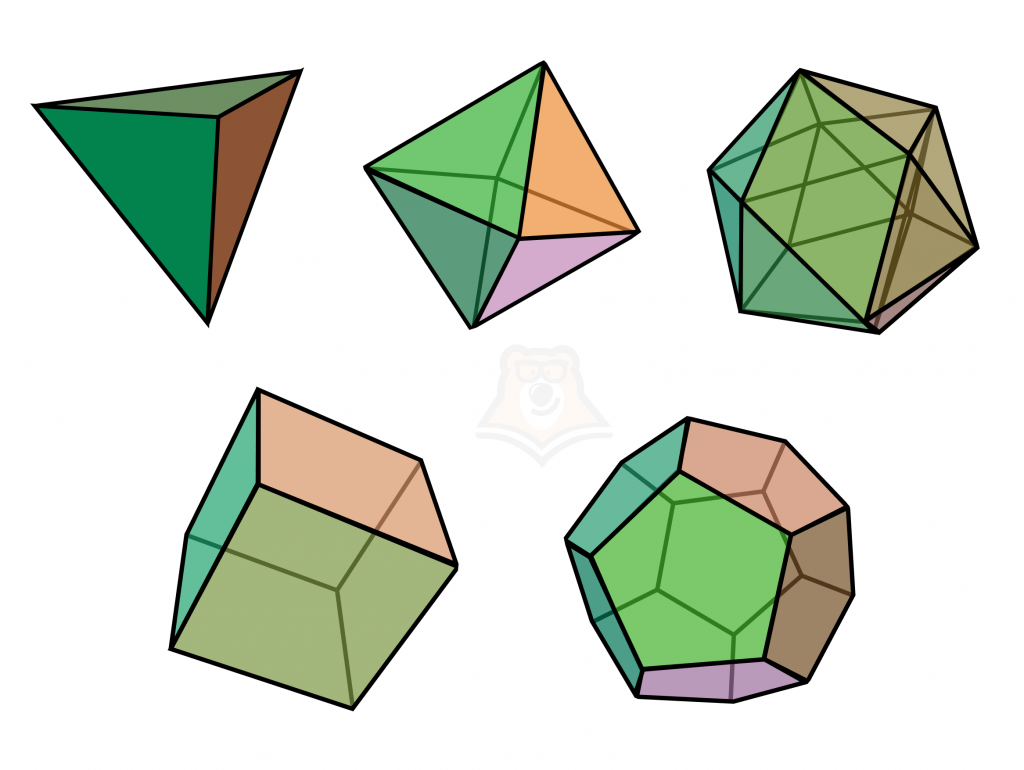
Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками – гранями.

К многогранникам относятся: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

Почему в геометрии не используют слово «похожи»? Представим, у нас есть два геометрических тела. На основании уже изученного материала мы сделали вывод, что они не равны, но очень похожи. Но в геометрии нет понятия «похожи» и «я же так сказал», мы не можем использовать аргумент «я так вижу», поэтому придется выучить определение подобных многогранников!

Два многогранника называются подобными, если они имеют соответственно равные многогранные углы и соответственно подобные грани.

Много непонятных терминов в одном предложении? Давайте разберем слова, которые могли вызвать трудности! 

Многогранный угол является пространственным аналогом многоугольника на плоскости. 

Напомним, что многоугольниками на плоскости называется фигура, образованная простой замкнутой ломаной этой плоскости и ограниченной ею внутренней областью.

Вы в детстве пытались какой-то предмет разобрать на составляющие? Думаем, да, если взять хотя бы детскую пирамидку. А как разобрать многогранник на элементы? Это очень даже возможно, но давайте начнем с простого. С того, как они называются и относятся друг к другу. 

Соответственные элементы подобных многогранников называются сходственными. 

У подобных многогранников двугранные углы равны и одинаково расположены; сходственные ребра пропорциональны.

Какие основные свойства нам нужны при решении задач с подобными телами?

• Если в пирамиде проведем секущую плоскость параллельно основанию, то она отсечет от нее другую пирамиду, подобную данной.
• Площади поверхностей подобных фигур связаны пропорционально квадрату коэффициента подобия (об этом мы поговорим подробнее чуть далее).
• Объемы подобных тел связаны пропорционально кубу коэффициента подобия.

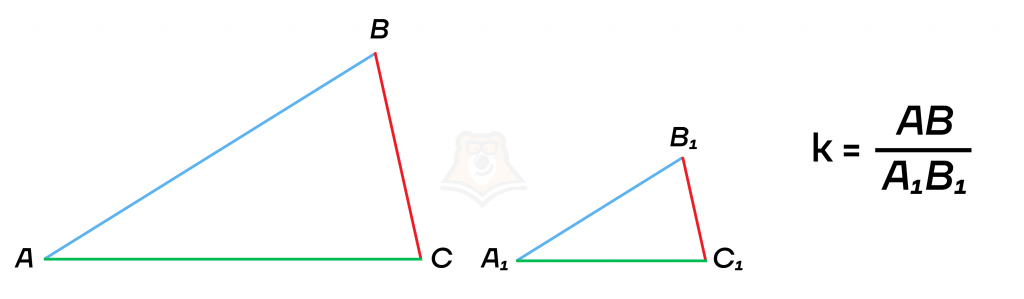
Что такое коэффициент подобия? 

Коэффициентом подобия называют число, равное отношению сходственных сторон подобных фигур.

Объем подобной фигуры можно найти, умножив объем исходной фигуры на куб коэффициента подобия.

С уже изученной информацией мы можем решать задачи на подобие. Сейчас этим и займемся!

Задача 1. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?

Решение:

Объемы подобных тел относятся как куб коэффициента подобия. Поэтому если все ребра увеличить в 3 раза, объем увеличится в 27 раз.

Ответ: 27 

Выглядит все довольно просто, поэтому давайте решим еще одну!

Задача 2. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 4 раза? 

Решение: 

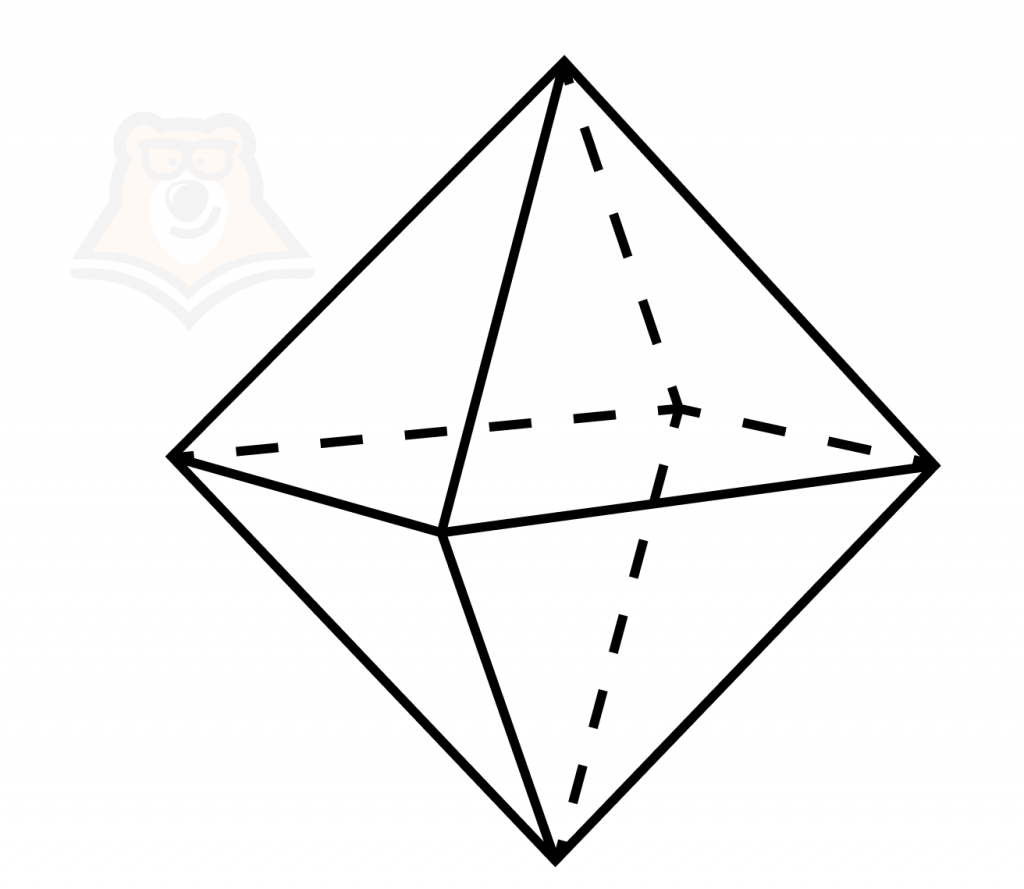
При увеличении ребер в 4 раза площади треугольников, образующих грани октаэдра, увеличатся в 16 раз, поэтому суммарная площадь поверхности также увеличится в 16 раз.

Ответ: 16

Условия подобных многогранников мы рассмотрели, теперь очередь цилиндров и конусов! 

Подобные цилиндры и конусы

Два цилиндра, конуса или усеченного конуса называются подобными, если подобны их осевые сечения.

Как обстоят «дела» с объемами подобных цилиндров и конусов? «Дела» у них отлично, но чтобы у нас «дела» были аналогичны, надо вспомнить, а может и изучить объемы!

Ранее мы рассмотрели основные свойства, связанные с коэффициентом подобия. Что же еще важно отметить?

• Объемы подобных цилиндров, конусов и усеченных конусов относятся, как кубы отношений их соответствующих линейных элементов (радиусов оснований, высот, образующих).
• Объемы шаров относятся, как кубы отношений их радиусов или диаметров.

Давайте запомним все вышесказанное с помощью применения знаний на практике.

Задача 3. Объем конуса равен 24. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение:

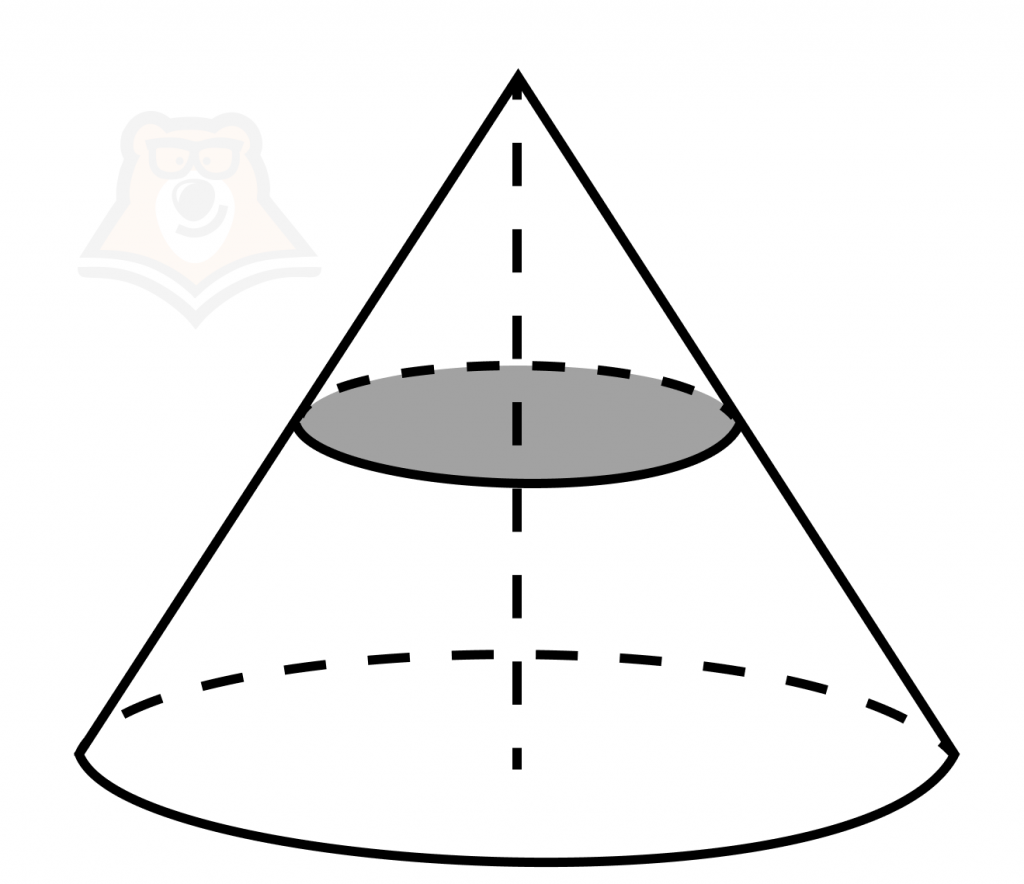
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса соотносится с объемом большего конуса как \(0,5^3=0,125\). Из этого следует, что объем маленького конуса будет равен 3.

Ответ: 3

Когда рассматривается объем подобных фигур, нельзя забывать про площади поверхностей подобных фигур. Давайте разберемся и с этой не сложной темой!  

Отношение площадей поверхностей подобных тел 

Прежде чем разбираться в теме, давайте вспомним, что такое площадь поверхности.

Площадь поверхности – это сумма площадей всех граней внешней оболочки тела.

Теперь мы готовы изучить формулу отношения площадей поверхностей подобных тел:

\(\frac{S_1}{s_2}=(\frac{a_1}{a_2})^2=k^2\)

где \(S_1, S_2\) — площади двух подобных поверхностей, а \(a_1, a_2\) — длины соответственных сторон 

Как быстро запомнить отношения подобных тел? Для удобства сделаем табличку со всеми отношениями: Для лучшего запоминания можно использовать эту табличку. Либо же есть знаменитая теорема, применяемая, когда речь идет об отношениях и коэффициенте подобия: Отношение площадей подобных фигур – это квадрат коэффициента подобия Отношение объемов подобных фигур – это куб коэффициента подобия

Чтобы использовать отношение коэффициентов и не путаться, надо лишь вспомнить единицу измерения того, что нам требуется. У объемов всегда тройка в степени у единиц измерения, у отрезков в степени единица, а у площади – квадрат. Связано это с измерениями: объемы у трехмерных фигур, площади – двухмерных.

Любую информацию надо закреплять на практике. Так давайте сделаем это и решим задачи, которые могут встретиться в ЕГЭ по профильной математике в номере 3.

Задание. Даны две правильные четырехугольные пирамиды. Объем первой пирамиды равен 9. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объем второй пирамиды.

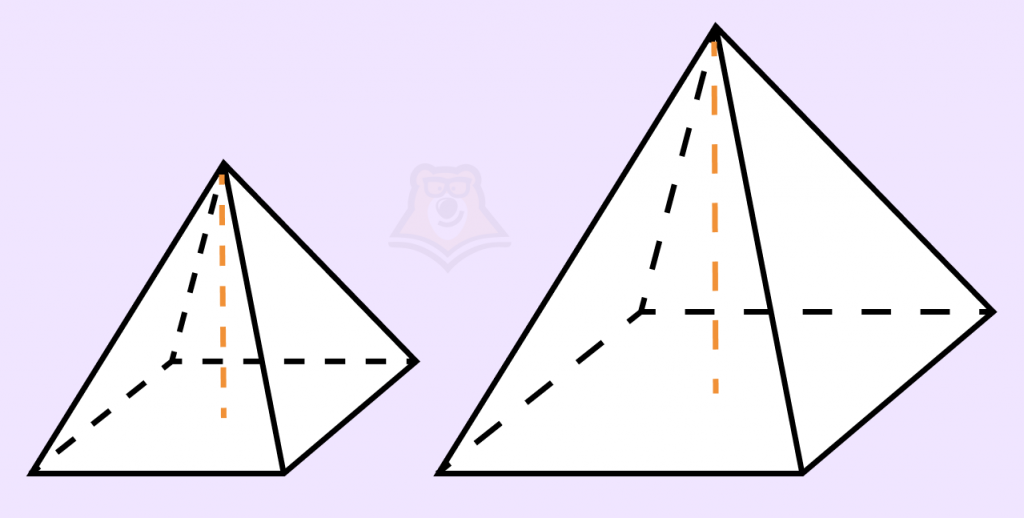
Решение:
Объем пирамиды вычисляется по формуле \(V=\frac{1}{3}Sh\).  Следовательно, отношение объемов пирамид: \(\frac{V_2}{V_1}=\frac{S_2H_2}{S_1V_1}=\frac{(1,5а_1)^2 2h_1}{a^2h_1}=4,5\)

Из этого следует, что объем пирамиды равен: \(9*4,5 = 40,5\)

Ответ: \(40,5\)

В этой статье мы разобрали, что такое подобие на примере плоскости и пространства. Изучили основные свойства, а также закрепили навыки на практике, решив множество задач. В следующей статье мы узнаем, что такое симметрия.

Фактчек

• Подобные фигуры и тела – это те геометрические объекты, которые имеют одинаковые пропорции, но разные размеры. Одну подобную фигуру можно получить из другой путем масштабирования (увеличения или уменьшения без изменения формы).
• Объем геометрических тел – это величина, которая описывает занимающую этим телом часть пространства или – это  положительная величина той части пространства, которую занимает геометрическое тело.
• Два многогранника называются подобными, если они имеют соответственно равные многогранные углы и соответственно подобные грани.
• Два цилиндра, конуса или усеченного конуса называются подобными, если подобны их осевые сечения.
• Отношение объемов подобных тел будет равно кубу отношения длин их соответствующих сторон. 
• Отношение площадей поверхностей подобных тел будет равно квадрату отношения длин их соответствующих сторон. 

Проверь себя

Задание 1.
Что из перечисленного не относится к многогранникам? 

1. Тетраэдр
2. Куб
3. Цилиндр
4. Октаэдр

Задание 2.
Как соотносятся объемы равных тел?

1. Они подобны
2. Они равны
3. О похожи
4. Они сходственны

Задание 3.
Как относятся объемы шаров?

1. Как кубы их радиусов или диаметров
2. Как квадраты их радиусов или диаметров
3. Как кубы площадей сечения
4. Как квадраты площадей сечения

Задание 4.
Закончить фразу. Площадь поверхности – это сумма площадей…

1. двух смежных граней;
2. любых трех граней;
3. противоположных граней;
4. всех граней их внешней оболочки.

Ответы: 1. — 3; 2. — 2; 3. —1; 4. — 4.