Интересные теоремы планиметрии
На этой странице вы узнаете
- Как бабочка связана с геометрией?
- Как без ошибок записать теоремы Менелая, Чевы и Ван-Обеля?
- Как трезубец мог оказаться в одной из теорем планиметрии, и как он связан с куриной лапкой?
В математике есть теоремы с необычными, интригующими названиями. Их трудно найти, легко недооценить, но невозможно хоть раз не применить.
Для решения простых планиметрических задач достаточно знать основные свойства и формулы фигур. Однако могут встретиться более сложные задачи, решение которых значительно упростится при применении некоторых редких теорем. Звучит немного пугающе, хотя ничего страшного в них нет. Напротив, многие из них очень увлекательные. Например, есть теоремы, связанные с бабочкой и трезубцем. Интересно? Давайте разбираться.
Теоремы для отрезков
Начнем изучать теоремы с отрезков.
Теорема Фалеса
Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, которые пересекут вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Разберемся в теореме чуть подробнее. Возьмем любые две прямые а и b и отложим на прямой а несколько точек А, B, C, D. Из этих точек проведем параллельные прямые, которые пересекут b в точках А1, В1, С1, D1 соответственно.
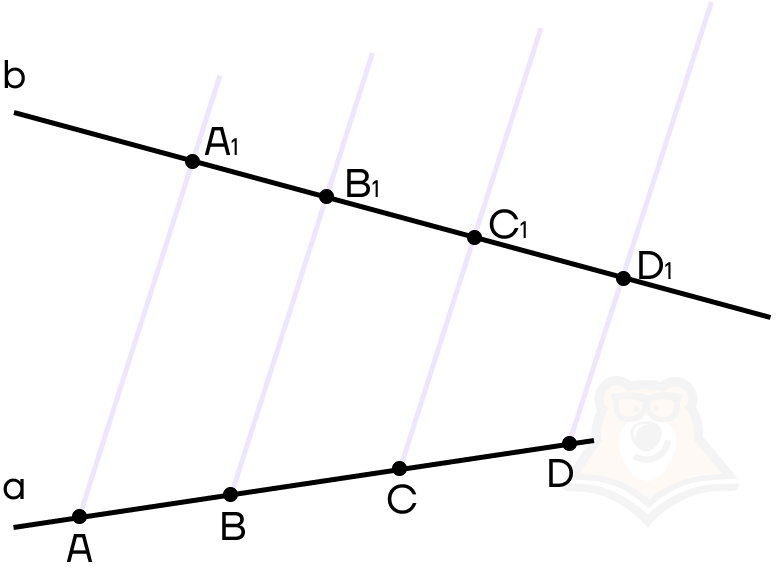
Поскольку по теореме Фалеса параллельные прямые отсекают пропорциональные отрезки, то будет выполняться следующее равенство:
\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{CD}{C_1D_1}Для чего можно применить теорему Фалеса:
- Если на одной из прямых отложить равные отрезки, то на второй прямой параллельные прямые также отсекут равные прямые.
Если мы вернемся к нашему рисунку и предположим, что AB = BC = CD, то также будет выполняться равенство A1B1 = B1C1 = C1D1.
- Если мы в решении задачи увидим, что прямые отсекают равные или пропорциональные отрезки, то можем смело писать, что такие прямые параллельны.
Теорема Фалеса достаточно простая и нередко может пригодиться в задачах, поэтому ее знание значительно облегчит решение.
Теперь разберем еще одну интересную теорему, однако она будет уже связана с отрезками в окружности, а именно с хордами.
Перед тем как привести определение теоремы, построим рисунок. Проведем в окружности хорду АВ с серединой в точке С. Через точку С построим еще две любые хорды DE и FG. Осталось только соединить точки Е и F, D и G. Также отметим точки пересечения DG и FE с АВ как Р и М соответственно, и наш рисунок готов.
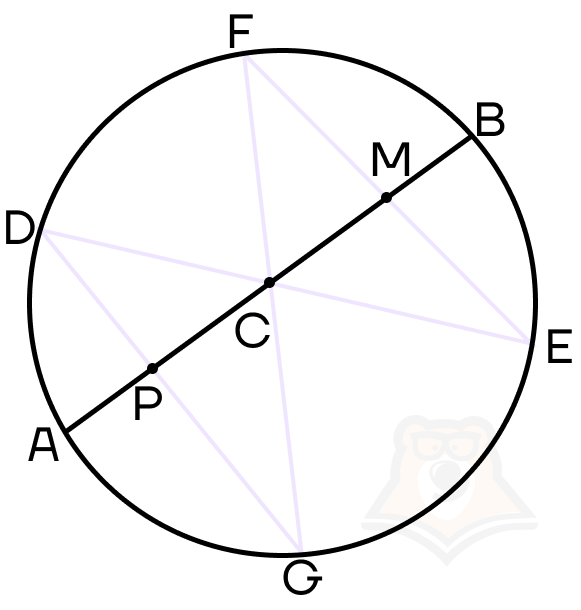
Теорема о бабочке
Если через середину С хорды АВ провести две произвольные хорды DE и GF, а прямые DG и FE пересекают АВ в точках Р и М соответственно, то выполняется равенство СР = СМ.
Разумеется, в построении могут быть использованы любые буквы и обозначения, однако смысл теоремы от этого не поменяется.
| Как бабочка связана с геометрией? Если посмотреть на рисунок для этой теоремы, то действительно похоже, будто бабочка сидит в окружности. |

А теперь разберем доказательство этой теоремы. На самом деле, для нее существует огромное количество доказательств, но остановимся мы только на одном из них. Для этого будем использовать те же обозначения и тот же рисунок, которые использовали для ее составления.
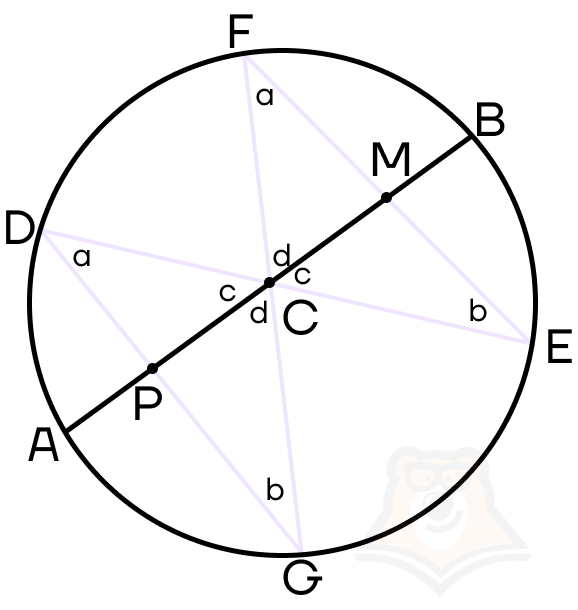
Рассмотрим рисунок и заметим равенство нескольких пар углов.
∠GDE = ∠GFE = a, ∠DGF = ∠DEF = b, как вписанные углы, опирающиеся на одну дугу.
∠DCP = ∠MCE = c, ∠FCM = ∠PCG = d, как вертикальные углы.
Также введем обозначение AC = CB = e (из условия), CP = x, CM = y.
1. Рассмотрим треугольник CPD и составим для него теорему синусов:
\frac{DP}{\sin c}=\frac{x}{\sin a} => DP=\frac{x*\sin c}{\sin a}Аналогично в треугольнике CPG:
\frac{GP}{\sin d}=\frac{x}{\sin b} => GP=\frac{x*\sin d}{\sin b}2. Рассмотрим хорды АВ и DG. Поскольку они пересекаются, выполняется равенство АР * РВ = DP * PG. Поскольку АР = АС — РС = е — х, PB = PC + CB = x + e, получаем:
(e-x)(e+x)=e^2-x^2=DP*PG=\frac{x*\sin c}{\sin a}*\frac{x*\sin d}{\sin b}=\frac{x^2*\sin c*\sin d}{\sin a*\sin b}3. Немного преобразуем уравнение
e^2-x^2=\frac{x^2*\sin c*\sin d}{\sin a*\sin b}e^2=x^2+x^2*\frac{\sin c*\sin d}{\sin a*\sin b}e^2=x^2(1+\frac{\sin c*\sin d}{\sin a*\sin b})x^2=\frac{e^2}{1+\frac{\sin c*\sin d}{\sin a*\sin b}}x=\frac{e} {\sqrt {1+\frac{\sin c*\sin d}{\sin a*\sin b}}}4. Если мы проведем такие же рассуждения с треугольниками FCM и СМЕ, то получим, что x = y, значит, теорема доказана.
Доказательство может выглядеть слишком объемным и пугающим, но оно все построено на алгебраических преобразованиях и теоремах геометрии.
Чтобы полностью разобраться в доказательстве, про вертикальные углы можно прочитать в статье «Точка, прямая, луч, отрезок и угол», про вписанные углы и свойства хорд можно прочитать в статье «Окружность и круг», а про теорему синусов в статье «Вписанная и описанная окружности. Основные формулы треугольника».
Теоремы для треугольника
Треугольники — наиболее часто встречающиеся фигуры в решении задач, и, конечно, для них существуют свои теоремы, которые очень удобно применять.
Начнем разбор этих теорем с теоремы Менелая. Для начала построим рисунок. Пусть треугольник АВС пересекает прямая ЕТ, причем Е — точка пересечения этой прямой и продолжения стороны ВС, Т — точка пересечения прямой и стороны АВ, М — точка пересечения этой прямой и стороны АС.
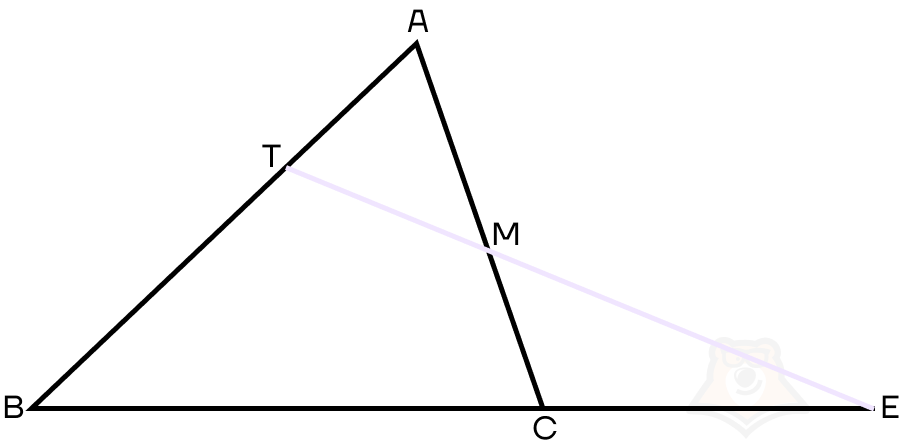
Теорема Менелая
Если прямая ЕТ пересекает стороны АВ, АС и ВС треугольника АВС в точках Т, М и Е соответственно, то выполняется равенство:
\(\frac{BT}{TA}*\frac{AM}{MC}*\frac{CE}{BE}=1\)
В теореме Менелая очень важен порядок, в котором составляется отношение. Если этот порядок нарушить, то теорема не будет выполняться.
Чтобы запомнить порядок, достаточно всегда следовать алгоритму. Оказывается, для составления теоремы достаточно обойти треугольник по периметру вот в таком порядке:
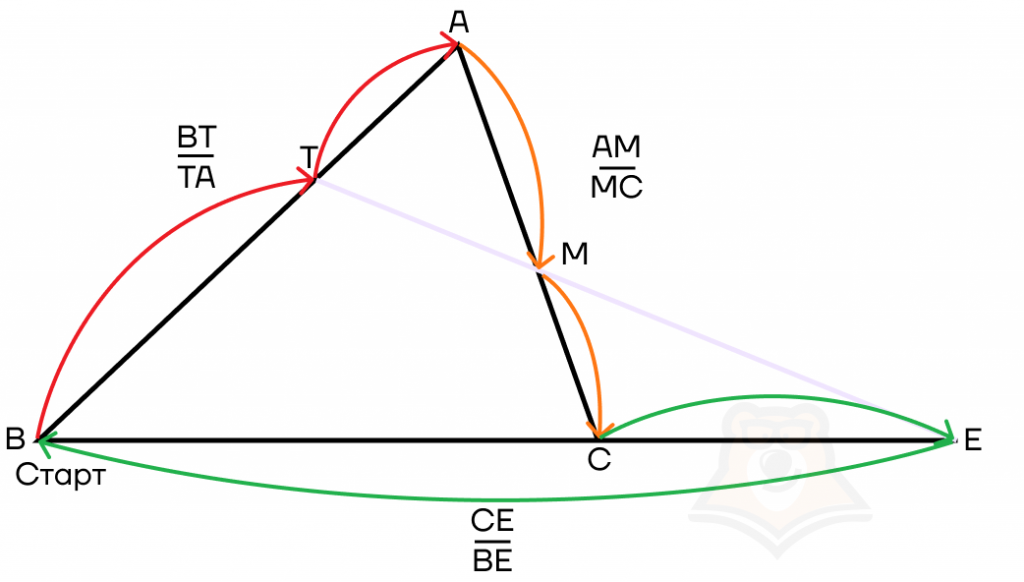
Теорема Менелая встречается в задачах намного чаще, чем может показаться на первый взгляд. А также удобно, что ее можно применять без доказательства.
Для треугольника существуют еще несколько теорем, две из которых опираются на понятие чевианы.
Чевиана — это отрезок, соединяющий вершину треугольника с точкой на противоположной ей стороне.
Начертим треугольник АВС с чевианами AD, ВЕ и СТ. Пусть чевианы пересекаются в точке О.
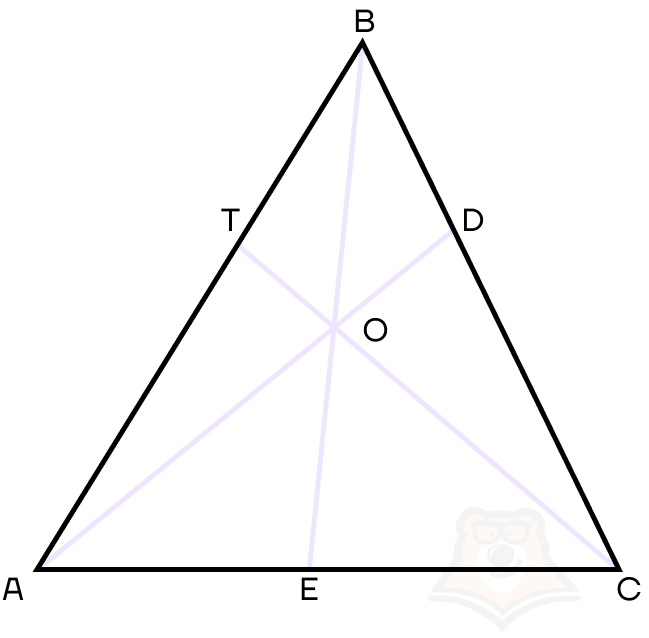
Теорема Чевы
Пусть АD, ВЕ, СТ — чевианы, которые пересекаются в точке О. Тогда выполняется следующее равенство:
\(\frac{AT}{TB}=\frac{BD}{DC}=\frac{CE}{EA}=1\)
Порядок отрезков в записи теоремы Чевы, как и в теореме Менелая, имеет особое значение. Чтобы не запутаться в их порядке, можно пользоваться следующей схемой:
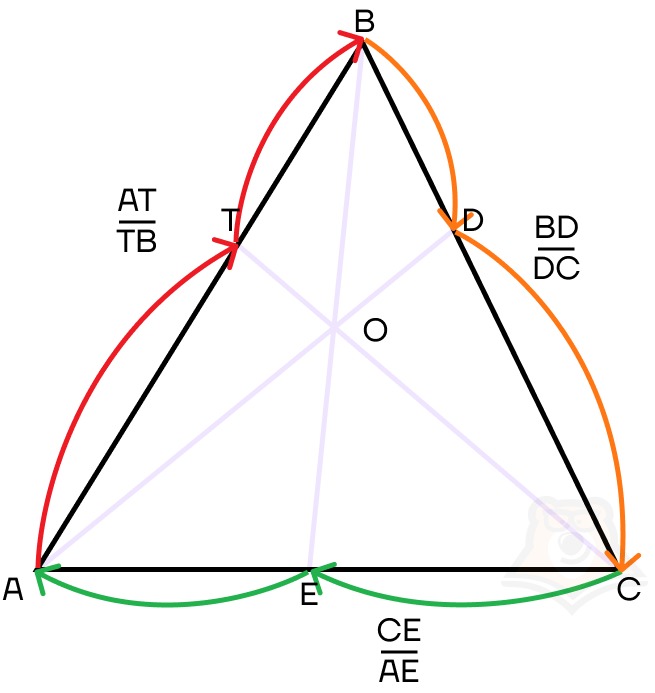
Докажем теорему Чевы.
1. Через вершину В треугольника АВС проведем прямую, параллельную АС. Продолжим чевианы СТ и AD до пересечения с этой прямой в точках М и Р соответственно.
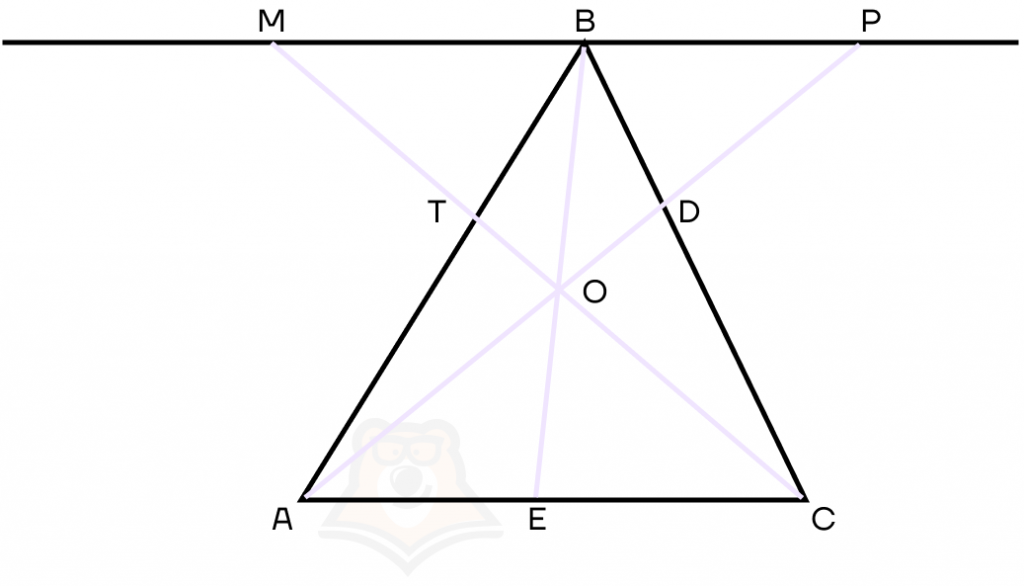
2. Заметим, что треугольники АТС и МВТ подобны по двум углам: ∠MBT = ∠TAC, как углы при параллельных прямых, ∠MTB = ∠ATC, как вертикальные углы.
Аналогично подобны треугольники BPD и ADC.
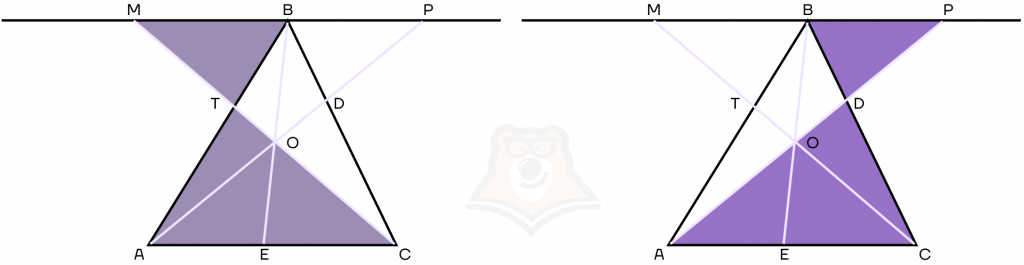
Составим отношения для подобных треугольников:
\frac{AT}{TB}=\frac{AC}{MB} и \frac{DB}{CD}=\frac{BP}{AC}3. Также выведем подобие треугольников ЕОС и ОВМ (подобны по двум углам ∠MBO = ∠OEC, ∠MOB = ∠EOC) и треугольников АОЕ и ОВР.

Из подобия этих треугольников получаем отношения:
\frac{EC}{MB}=\frac{EO}{OB} и \frac{AE}{BP}=\frac{EO}{OB}Следовательно,
\frac{EC}{MB}=\frac{AE}{BP} =>\frac{EC}{AE}=\frac{MB}{BP}4. Если мы перемножим полученные уравнения, то как раз получим теорему Чевы:
\frac{AT}{TB}=\frac{BD}{DC}=\frac{CE}{EA}=1Рассмотрим еще одну теорему, связанную с чевианами, а именно теорему Ван-Обеля.
Теорема Ван-Обеля
Пусть AD, ВЕ и СТ — чевианы, пересекающиеся в точке О. Тогда выполняется следующее равенство:
\(\frac{BO}{OE}=\frac{BD}{DC}+\frac{BT}{TA}\)
В теореме Ван-Обеля также важно расположение отрезков в уравнении. Запомнить их можно по этой схеме:
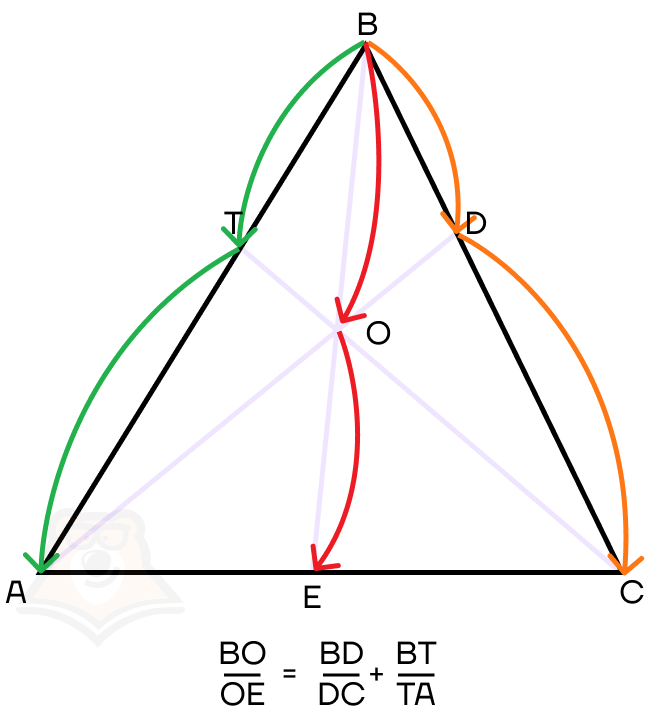
| Как без ошибок записать теоремы Менелая, Чевы и Ван-Обеля? Поскольку в этих теоремах отношения отрезков должны быть записаны в строгом порядке (иначе теоремы просто не будут выполняться), необходимом пользоваться алгоритмом записи. Схемы, как правильно составить теоремы, приведены в тексте выше. Важно заметить, что треугольники могут быть повернуты или отзеркалены, однако вне зависимости от их положения порядок отрезков в теоремах меняться не может. Следовательно, схемы их составления могут также менять свое положение, но последовательность должна остаться прежней. |
Так же как и теорема Чевы, теорема Ван-Обеля доказывается с помощью подобных треугольников.
1. Через вершину В треугольника АВС проведем прямую, параллельную АС. Продолжим чевианы СТ и AD до пересечения с этой прямой в точках М и Р соответственно.
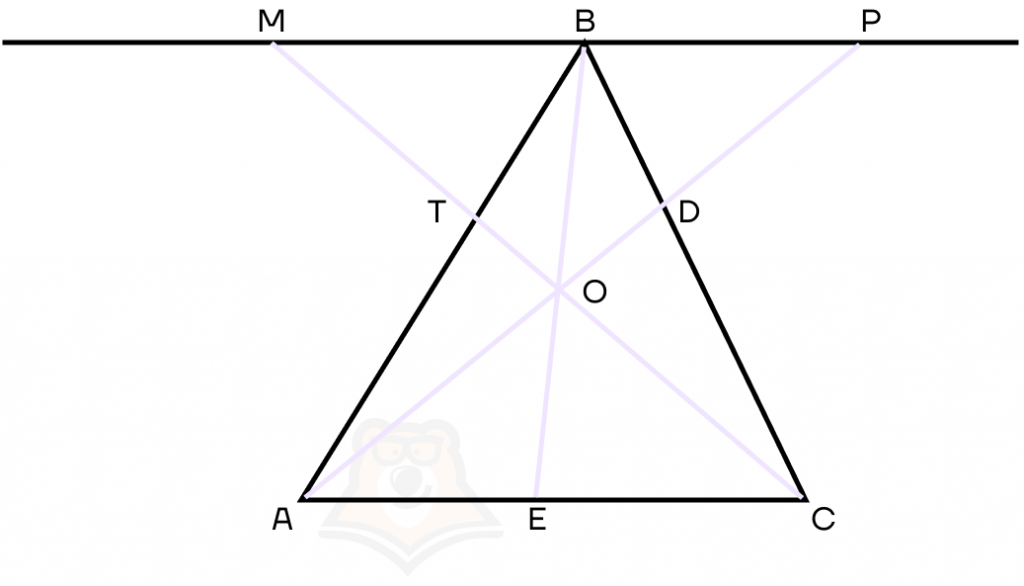
2. Треугольник АОС подобен треугольнику ОРМ по двум углам: ∠AOC = ∠MOP — вертикальные, ∠PMO = ∠OCA — углы при параллельных прямых.
Следовательно, для этих треугольников выполняется отношение
\frac{OP}{AO}=\frac{MP}{AC}Треугольники АОЕ и ОВР подобны по двум углам: ∠BOP = ∠AOE — вертикальные, ∠OBP = ∠OEA — углы при параллельных прямых.
Из подобия этих треугольников выполняется отношение
\frac{BO}{OE}=\frac{OP}{AO}Таким образом, получаем уравнение
\frac{BO}{OE}=\frac{MP}{AC}=\frac{MB+BP}{AC}=\frac{MB}{AC}+\frac{BP}{AC}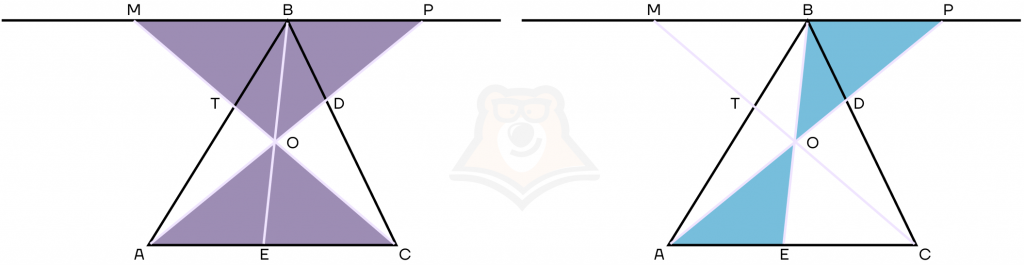
3. Треугольники ADC и DBP подобны по двум углам, тогда мы получаем равенство
\frac{BD}{DC}=\frac{BP}{AC}Треугольники МТВ и АТС подобны по двум углам — получаем равенство
\frac{TB}{AT}=\frac{MB}{AC}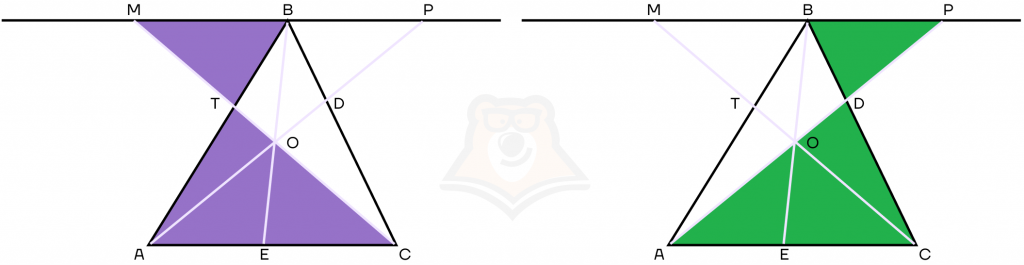
Следовательно, получаем уравнение:
\frac{BO}{OE}=\frac{MB}{AC}+\frac{BP}{AC}=\frac{TB}{AT}+\frac{BD}{DC}Теорема Ван-Обеля доказана.
В доказательствах теорем Чевы и Ван-Обеля активно используется подобие треугольников. Чуть подробнее про это можно прочитать в статье «Равенство и подобие треугольников».
Завершим рассказ о теоремах в треугольнике Леммой о трезубце.
Для начала выполним рисунок.
Построим треугольник АВС. Впишем в него окружность с центром в точке О, а также опишем вокруг него окружность с центром в точке Е. Достроим вневписанную окружность, которая касается стороны АС и продолжения сторон ВА и ВС. Центр вневписанной окружности будет лежать в точке М.
Вневписанная окружность — это окружность, которая касается стороны треугольника и продолжения двух других его сторон.
Иными словами, она очень похожа на вписанную окружность, но лежит за пределами треугольника.
Построим биссектрису угла В. Вспомним, что центр вписанной в треугольник окружности лежит в точке пересечения биссектрис, следовательно, биссектриса пройдет через точку О. Продлим биссектрису до пересечения с описанной окружностью в точке Т.
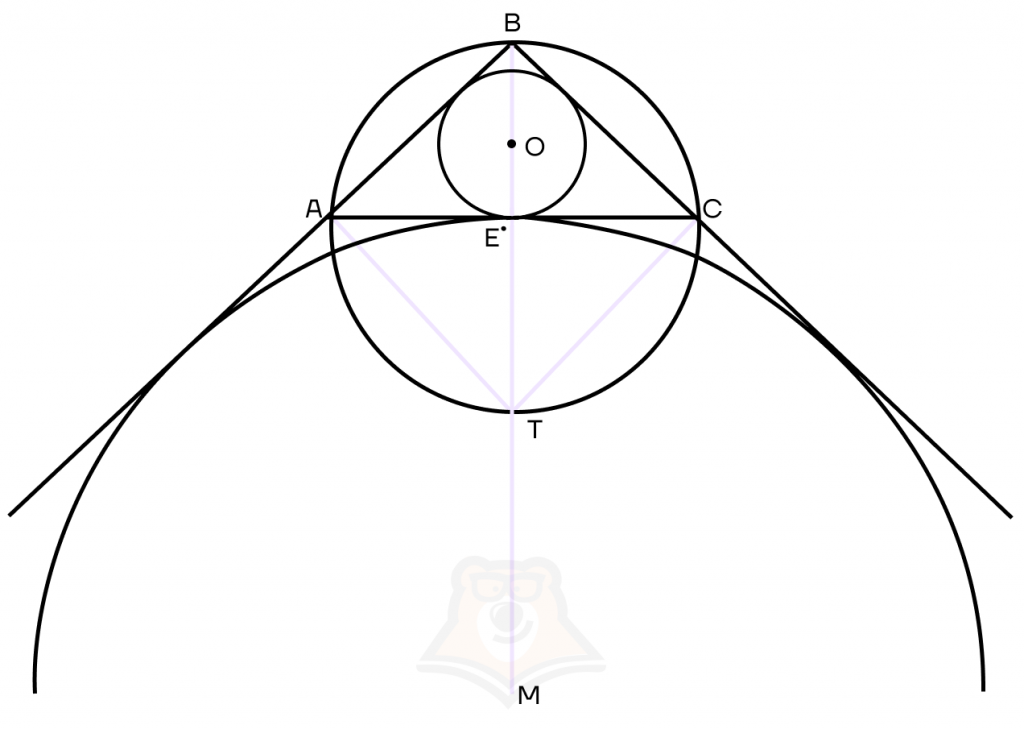
Лемма о трезубце
Пусть О — центр вписанной окружности, М — центр вневписанной окружности, ВТ — биссектриса угла В, которая пересекает описанную окружность в точке Т. Тогда точка Т будет равноудалена от точек М, А, О, С, то есть будет выполняться равенство МТ = ТА = ТО = ТС.
| Как трезубец мог оказаться в одной из теорем планиметрии, и как он связан с куриной лапкой? Может появиться вопрос к названию теоремы, причем здесь трезубец? Однако если внимательно присмотреться к чертежу, то можно заметить, что построение похоже на трезубец. Иногда эту же лемму называют леммой о трилистнике и даже леммой о куриной лапке. |
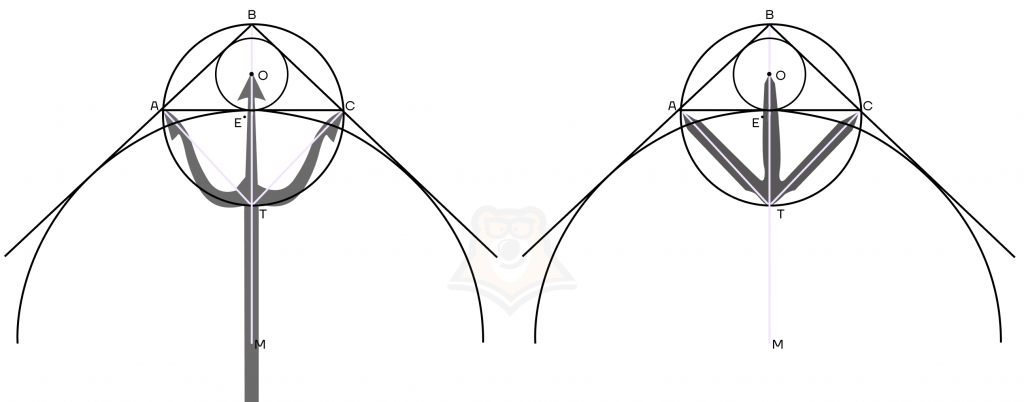
Разберем доказательство леммы о трезубце. Для этого начнем с доказательства, что AT = TO.
1. Достроим треугольник АТО. Обозначим в треугольнике АВС углы ∠ABO = ∠OBC = b, поскольку ВО — биссектриса. Достроим прямую АО — также биссектрису, и обозначим углы ∠BAO = ∠OAC = a.
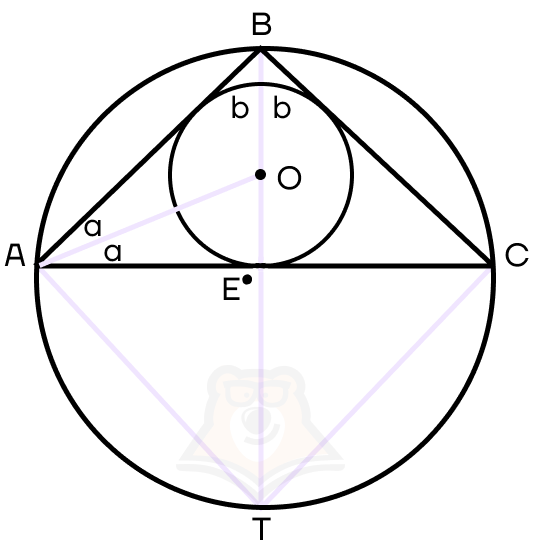
Заметим, что ∠CAT = ∠CBT = b, как вписанные углы, опирающиеся на одну дугу. Следовательно, ∠CAT = b, ∠OAT = a + b.
Рассмотрим треугольник АОВ, в котором угол АОВ равен 180 — a — b.
Углы ∠АОВ и ∠АОТ — смежные, следовательно, ∠АОТ = 180 — (180 — a — b) = a + b.
Получаем, что ∠АОТ = ∠ОАТ, значит, треугольник АОТ — равнобедренный, тогда AT = TO.
В треугольнике ОСТ подобным образом можно доказать равенство OT = TC.
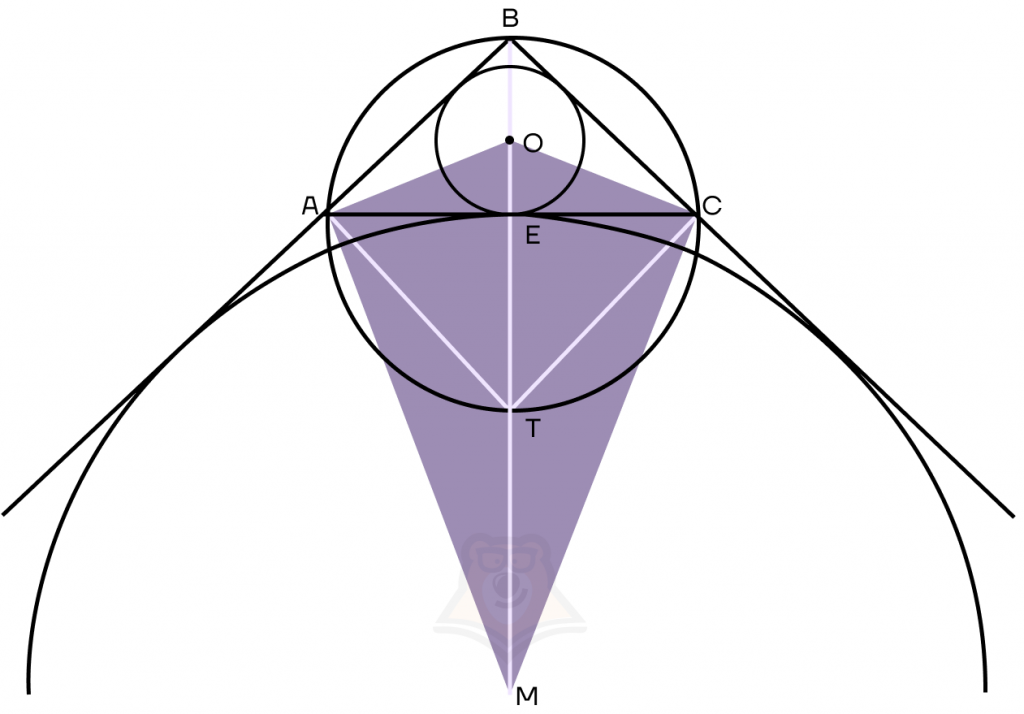
2. Осталось доказать, что TM = TO.
Заметим, что АО и АМ — биссектрисы углов ВАС и САМ. Следовательно, угол ОАМ равен 90°, поскольку является углом между биссектрисами двух смежных углов. Аналогично получаем, что угол ОСМ — прямой.
Поскольку сумма углов ∠ОАМ + ∠ОСМ = 180°, то четырехугольник можно вписать в окружность с диаметром ОМ.
Поскольку AT = TC = TO из предыдущего пункта доказательства, и точки А, О, С лежат на окружности, то AT = TC = TO = R. Из этого вытекает, что ОТ — половина диаметра ОМ, откуда OT = TM.
Лемма о трезубце доказана.
Теоремы в четырехугольнике
Завершим рассказ об интересных теоремах планиметрии теоремами в четырехугольнике. Одна из них, а именно теорема Птолемея, уже была рассмотрена в статье «Вписанная и описанная окружность».
В этой статье разберем теорему Вариньона.
Теорема Вариньона
Середины сторон произвольного выпуклого четырехугольника являются вершинами параллелограмма.
Начертим произвольный четырехугольник ABCD и отметим середины его сторон АВ, ВС, СD, AD точками М, Е, Т, К соответственно. Тогда по теореме Вариньона МЕТК — параллелограмм. Докажем это.
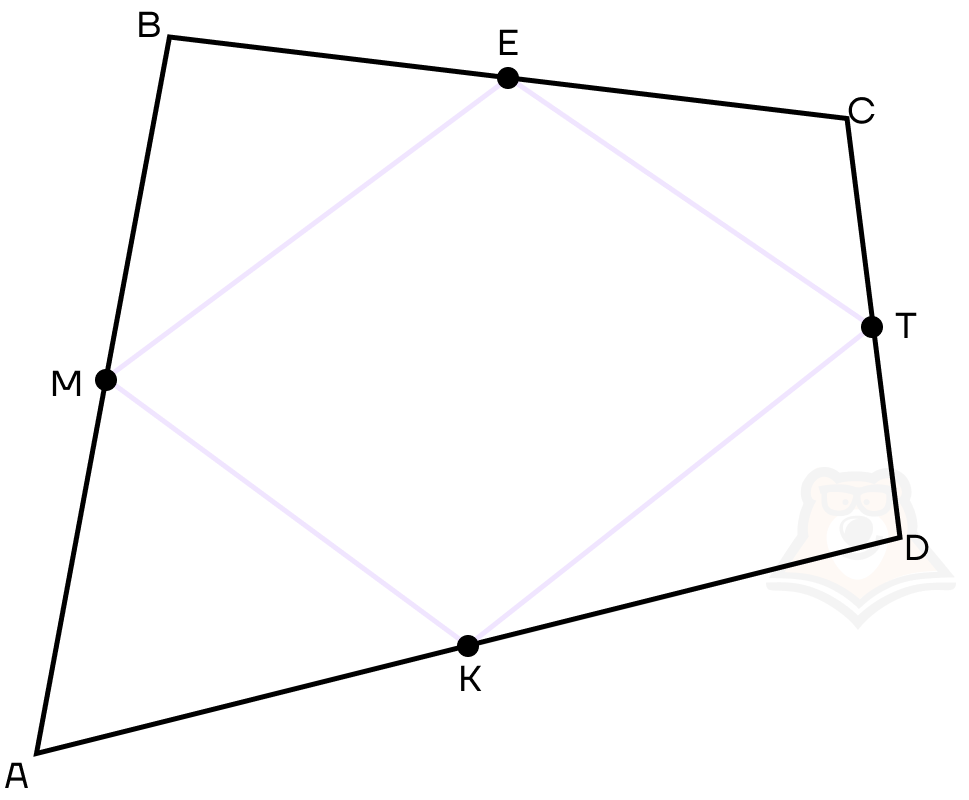
1. Проведем диагонали АС и BD в четырехугольнике ABCD.
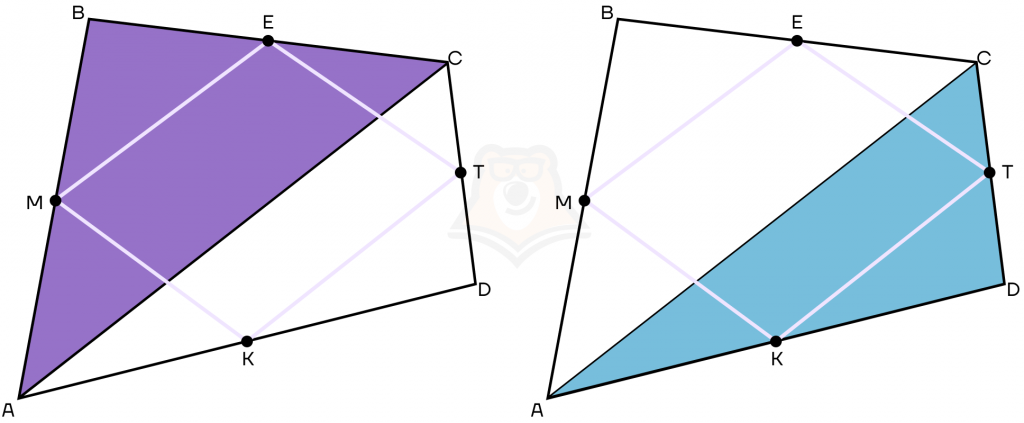
Рассмотрим треугольник АВС, в котором МЕ — средняя линия. Следовательно, получаем равенства AM = MB, CE = BE, AC = 2ME. Также МЕ || АС.
2. Рассмотрим треугольник ACD, в котором ТК — средняя линия. Следовательно, получаем равенства AK = KD, DT = TC, AC = 2KT. Также КТ || АС.
3. Из этих двух треугольников получаем: 2ME = 2KT, тогда ME = KT и МЕ || КТ. По признаку параллелограмма получаем, что МКЕТ — параллелограмм.
Мы рассмотрели несколько теорем, знание которых может значительно облегчить решение сложных планиметрических задач. Каждая из них совсем несложная, но именно их знание могут дать преимущества.
Фактчек
- В планиметрии существует множество интересных, но редких теорем, использование которых может значительно упростить решение задач.
- Для отрезков среди этих теорем можно выделить теорему Фалеса и теорему о бабочке. С помощью теоремы Фалеса можно доказать параллельность прямых или найти отрезки, которые эти параллельные прямые отсекают.
- Для треугольников можно выделить теоремы Менелая, Чевы, Ван-Обеля и лемму о трезубце. В теоремах Чевы и Ван-Обеля используются чевианы — отрезки, которые соединяют вершину треугольника и его противоположную сторону.
- В четырехугольниках можно выделить теоремы Птолемея и Вариньона. Теорема Вариньона гласит, что середины сторон произвольного выпуклого четырехугольника являются вершинами параллелограмма.
Проверь себя
Задание 1.
Известно, что некоторые прямые отсекают на двух сторонах многоугольника пропорциональные отрезки. Какими являются эти прямые?
- параллельные
- перпендикулярные
- произвольными
- невозможно сказать, какими будут прямые
Задание 2.
В какой из теорем используются чевианы?
- Теорема Менелая
- Теорема Ван-Обеля
- Теорема Вариньона
- Теорема о бабочке
Задание 3.
Что такое вневписанная окружность?
- Это другое название описанной окружности.
- Это другое название вписанной окружности.
- Это окружность, которая касается одной из сторон треугольника и продолжения двух других его сторон.
- Это окружность, которая не имеет с треугольником общих точек.
Задание 4.
Вершинами какой фигуры являются середины произвольного выпуклого четырехугольника?
- параллелограмма
- трапеции
- произвольного четырехугольника
- невозможно определить фигуру, не зная данные четырехугольника
Ответы: 1. — 1; 2. — 2; 3. — 3; 4. — 1.


 к списку статей
к списку статей