Однородные уравнения

На этой странице вы узнаете

• Как математики смогли «заменить» Нобелевскую премию?
• В чем парадокс деления на ноль?
• Где еще, кроме школы, можно встретиться с однородными уравнениями?

Почему математикам не дают Нобелевскую премию? Есть две версии: первая – Нобель очень не любил шведского математика и из-за него не стал включать математику в список наук, за которые дается премия, а вторая – математика является теоретической наукой, вспомогательной для более прикладных областей знаний: физика, химия, экономика.

Как математики смогли «заменить» Нобелевскую премию? Хотя математикам не дают Нобелевскую премию, ученые, занимающиеся ей, также могут получить престижную награду. Например, математики до 40 лет могут удостоиться Филдсовской премии, которую вручают раз в четыре года, а математики любого возраста могут получить Абелевскую премию, которая присуждается ежегодно.

Точного ответа на вопрос, почему математики не получают Нобелевскую премию, мы узнать, к сожалению, не сможем. Но версия про теоретическую науку кажется более правдоподобной, поэтому сегодня мы рассмотрим уравнения, которые действительно очень помогают в описании физических процессов. Эти уравнения называются однородными.  

Однородное уравнение – уравнение, все слагаемые которого имеют одинаковую степень и не имеющие свободных членов. 

В таких уравнениях в левой части все одночлены имеют одинаковую степень, справа 0, либо уравнение можно привести к такому виду. 

В этой статье мы разберем, чем этот тип уравнений отличается от других и как их решать.

Однородные уравнения

Однородное уравнение – уравнения вида
\(a_0f^n+a_1f^{n-1}g+a_2f^{n-2}g^2+ … +a_{n-1}fg^{n-1}+a_ng^n=0\) с двумя неизвестными функциями. 

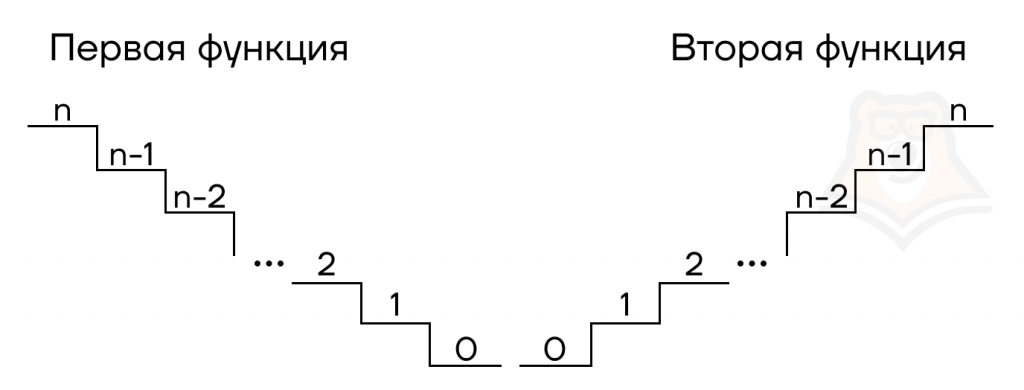
Это очень похоже на лестницу, в случае одной функции мы спускаемся по ней, идем с \(n\)-ой ступени к нулевой: \(n, n-1, n-2, …, 1, 0\). С другой же функцией мы по лестнице поднимаемся: \(0, 1, …, n-2, n-1, n\). Здесь \(n\) — любое натуральное число, от его величины зависит только «длина» нашей лестницы.

Рассмотрим примеры таких уравнений:

• \(2x^2+3xy+y^2=0\)
• \(2sinx+9cosx=0\)
• \(4*9^x+6*4^x*3^x+18*16^x=0\). Преобразуем уравнение и получим:
  \(4*3^{2x}+6*4^x*3^x+18*4^{2x}=0\)

Если в каждом из этих уравнений сложить степени каждого слагаемого, эти суммы будут одинаковыми. Например, в первом уравнений сумма степеней первого слагаемого равна 2, второго – также 2 (1+1), и степень третьего слагаемого также 2. 

Однородные уравнения обладают важным свойством: мы можем умножить функции, которые являются решениями на одну и ту же константу, и эти функции все равно будут решениями исходного уравнения. 

Это чем-то похоже на подобные треугольники: меняя размер треугольника, мы никак не изменяем его пропорции. По сути, это тот же треугольник только больших или меньших размеров. 

Например, пусть пара (\(x,y\)) решение уравнения \(2x^2+3xy+20y^2=0\), тогда пара (\(tx, ty\)) также решение. Проверим это: \(2(tx)^2+3tx*ty+20(ty)^2=0\), можем разделить обе части уравнения на \(t^2\) и тогда получим исходное уравнение, значит (\(tx, ty\)) действительно решение. 

Разобравшись с терминологией, самое время перейти к практике!

Решение однородных уравнений

Любые однородные уравнения решаются делением обеих частей на одну из функции в большей степени с учетом того, что она не равна нулю. Далее необходимо совершить замену переменной и решить получившееся линейное или квадратное уравнение.

Подробнее о решении квадратных и линейных уравнений можно прочитать в статье «Линейные, квадратные и кубические уравнения».

Алгоритм решения однородного уравнения:

1 шаг: Разделить обе части уравнения на одну из функций в большей степени, с учетом того, что эта функция не равна нулю.
Уравнение \(a_0f^n+a_1f^{n-1}g+a_2f^{n-2}g^2+ … +a_{n-1}fg^{n-1}+a_ng^n=0\) необходимо разделить или на \(f^n\), или на \(g^n\).

2 шаг: Сделать замену переменных.

3 шаг: Решить получившееся уравнение.

4 шаг: Сделать обратную замену.

Рассмотрим, как решать основные типы однородных уравнений: однородные тригонометрические и показательные уравнения. 

Однородные тригонометрические уравнения

Однородные тригонометрические уравнения бывают двух типов:
1. однородное тригонометрическое уравнение первой степени – \(acos{x}+bsin{x}=0\)
2. однородное тригонометрическое уравнение второй степени – \(acos^2x+bcos{x}sin{x}+csin^2x=0\)

Разберем алгоритм решения на примере тригонометрического однородного уравнения: \(3sinx+2cosx=0\).

Наибольшая степень функций – единица, разделим обе части уравнения на \(cosx ≠ 0\). Это действительно верно, потому что если \(cosx = 0\), то \(sinx = 1\) или \(-1\), тогда \(-3=0\) или \(3=0\), что невозможно.

В чем парадокс деления на ноль? Деление на ноль невозможно, так как умножение любого числа на ноль дает в итоге ноль. Тогда, разделив любое число, отличное от нуля, на ноль, мы, получая любую константу, нарушим это правило. Например, попробуем разделить натуральное число на ноль: \(\frac{7}{0}=x\). Тогда \(0*x=7\), но это невозможно, какое бы число вместо x мы ни взяли.

\(3\frac{sinx}{cosx}+2\frac{cosx}{cosx}=0\)

Преобразуем выражение по формуле \(\frac{sin x}{cos x}=tg x\): 

\(3tgx+2=0\)
Пусть \(t =tgx\)
\(3t+2=0\)
\(3t=-2\)
\(t=-\frac{2}{3}\)

Произведем обратную замену:

\(tgx=-\frac{2}{3}\)

Решим простейшее тригонометрическое уравнение:

\(x = arctg(-\frac{2}{3})+πn, n ∊ Z\)
\(x =-arctg(\frac{2}{3})+πn, n ∊ Z\)

Тригонометрические однородные уравнения встречаются в задании №12 ЕГЭ (№13 в ЕГЭ 2024 года) по профильной математике.

Задание. а) Решите уравнение \(2sin2x+4cos^2x=-2cos2x\)
б) Укажите корни этого уравнения, принадлежащие отрезку \([π; \frac{3π}{2}]\)

Решение. a) Перенесем все слагаемые в левую сторону: 

\(2sin2x + 4cos^2x+2cos2x=0\)

Раскроем тригонометрические формулы:

\(sin2x = 2sinxcosx\)
\(cos2x=cos^2x-sin^2x\)

Тогда \(4sinxcosx+4cos^2x+2(cos^2x-sin^2x)=0\)
\(4sinxcosx+4cos^2x+2cos^2x-2sin^2x=0\)
\(4sinxcosx+6cos^2x-2sin^2x=0\)
\(6cos^2x+4sinxcosx-2sin^2x=0 | :2\)

Поскольку мы решаем однородное уравнение, нам необходимо его разделить на функцию в большей степени, то есть на квадрат косинуса или квадрат синуса. Разделим на косинус: 

\(3cos^2x + 2sinxcosx-sin^2x=0 | : cos^2x ≠ 0\)

\(cos^2x ≠ 0\), так как если \(cosx=0\), то \(sinx=1\) или \(-1\), тогда \(-1=0\), что невозможно.

\(3+2\frac{sinx}{cosx}-(\frac{sinx}{cosx})^2=0\)

Поскольку \(\frac{sinx}{cosx}=tgx\), то:

\(-tg^2x+2tgx+3=0\)
Пусть \(t = tgx\)
\(-t^2+2t+3=0\)

Решим квадратное уравнение:

\(D =b^2-4ac = 2^2-4*3*(-1)=4+12=16\)
\(t_1=\frac{-b-\sqrt{D}}2a=\frac{-2-4}{-2}=3\)
\(t_2=\frac{-b+\sqrt{D}}2a=\frac{-2+4}{-2}=-1\)

Обратная замена:

\(tgx = 3\) или \(tgx=-1\)
\(x = arctg(3)+πn, n ∊ Z\) или \(x = arctg(-1)+πn =-\frac{π}{4}+πn, n ∊ Z\)

б) Отберем корни с помощью тригонометрической окружности

Ответ: а) \(arctg(3)+πn, -\frac{π}{4}+πn, n ∊ Z\)
б) \(arctg(3)+π\)

Однородные уравнения также могут быть показательными.

Однородные показательные уравнения

Однородные показательные уравнения бывают двух типов:
1. однородное показательное уравнение первой степени – \(af^x+bg^x=0\)
2. однородное показательное уравнение второй степени – \(af^{2x}+bf^xg^x+cg^{2x}=0\)

В случае показательных однородных уравнений мы действуем так же, как и в тригонометрических однородных уравнениях, то есть делим на член со старшей степенью.

Рассмотрим, как действовать на примере однородного показательного уравнения первой степени:

\(4^x=\frac{3}{4}*3^x\)

Разделим обе части уравнения \(3^x ≠ 0\), так как натуральное число в любой степени больше нуля. 

\((\frac{4}{3})^x=\frac{3}{4}\)
\((\frac{4}{3})^x=(\frac{4}{3})^{-1}\)
\(x=-1\)

Разберем показательное однородное уравнение, которое может встретиться в ЕГЭ по профильной математике в задании №13.

Задание. а) Решите уравнение \(9^x-7*6^x+12*4^x=0\)
б) Укажите корни этого уравнения, принадлежащего отрезку \([1; 3]\).

Решение. Преобразуем исходное уравнение: \(3^{2x}-7*3^x*2^x+12*2^{2x}=0\)

Разделим уравнение на \(2^{2x} ≠ 0\), так как положительное число всегда больше нуля.

\((\frac{3}{2})^{2x}-7*(\frac{3}{2})^x+12=0\)
Пусть \(t = (\frac{3}{2})^x\)
\(t^2-7t+12=0\)
\(D =b^2-4ac = (-7)^2-4*12=49+48=1\)
\(t_1=\frac{-b-\sqrt{D}}{2a}=\frac{7-1}{2}=3\)
\(t_2=\frac{-b+\sqrt{D}}{2a}=\frac{7+1}{2}=4\)

Обратная замена:

\((\frac{3}{2})^x=3\) или \((\frac{3}{2})^x=4\)
\(x = log_{\frac{3}{2}}3\) или \(x= log_{\frac{3}{2}}4\)

б) Отбор корней на отрезке:

\((\frac{3}{2})^x=3\)
\((\frac{3}{2})^1<3<(\frac{3}{2})^3\)
\((\frac{3}{2})^1<(\frac{3}{2})^x<(\frac{3}{2})^3\)
\(1<x<3\)

Следовательно, \(x = log_{\frac{3}{2}}3 ∊ [1; 3]\).

\((\frac{3}{2})^x=4\)
\((\frac{3}{2})^3<4\)
\((\frac{3}{2})^3<(\frac{3}{2})^x\)
\(x>3\)

Следовательно, \(x = log_{\frac{3}{2}}4 ∉ [1; 3]\).

Ответ: a) \(log_{\frac{3}{2}}3, log_{\frac{3}{2}}4\)
b) \(log_{\frac{3}{2}}3\)

Однородные уравнения – важнейший математический инструмент, который используется в различных сферах, без них сложно представить современную математику в том виде, в котором мы ее знаем сейчас. 

Где еще, кроме школы, можно встретиться с однородными уравнениями? При изучении высшей математики в университете появляется новый тип уравнений – дифференциальные уравнения, то есть те, в которых участвует не только функция, но и ее производная. Один из видов дифференциальных уравнений – однородные дифференциальные уравнения, которые также обладают свойством «обычных» однородных уравнений: если (x, y) – решение исходного однородного дифференциального уравнения, то (tx, ty) также решение.

Чтобы уже сейчас начать готовиться к учебе в  университете, читайте нашу следующую статью «Производная».

Термины

Константа – величина, значение которой не меняется. 

Замена переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Фактчек

• Однородное уравнение – это уравнение с двумя переменными без свободного коэффициента, а в каждом из слагаемых наблюдается одинаковая сумма степеней.
• Свойство однородного уравнения: если пара (x, y) – решение однородного уравнения, пара (tx, ty) также решение.
• При решении однородных уравнений мы должны разделить обе части этого уравнения на одну из функций уравнения в большей степени с учетом того, что эта функция не равна нулю.

Проверь себя

Задание 1.
Какое уравнение является однородным?

1. \(3x+y^2=0\)
2. \(3sin^3x-cos^2x=0\)
3. \(5^x+5^x*7^x=0\)
4. \(5x^3-4x^2y+6xy^2+3y^3=0\)

Задание 2.
Если пара чисел (3,2) является решением однородного уравнения, какая пара чисел также будет решением?

1. (6, 6)
2. (5, 4)
3. (9, 6)
4. (4, 3)

Задание 3.
Что является решением однородного уравнения \(2x^2-xy-y^2=0\)?

1. \(x=2, y=2\)
2. \(x=1, y=3\)
3. \(x=2, y=-2\)
4. \(x=-2, y=2\)

Задание 4.
Что является решением уравнения \(5^x=6^x\)?

1. \(0,5\)
2. \(0\)
3. \(1\)
4. \(2\)

Задание 5.
Что является решением уравнения \(cos^2x+2*cosx*sinx-5sin^2x=0\)?

1. \(x = arcctg(-1-\sqrt{6})+πn;arcctg(1+\sqrt{6})+πn, n ∊ Z\)
2. \(x = arcctg(-1-\sqrt{6})+πn, n ∊ Z\)
3. \(arcctg(1+\sqrt{6})+πn, n ∊ Z\)
4. \(x = arcctg(-1-\sqrt{6})+πn;arcctg(-1+\sqrt{6})+πn, n ∊ Z\)

Ответы: 1. — 4; 2. — 3; 3. — 1; 4. — 2; 5.— 4.