Основные элементарные функции. Часть 1

На этой странице вы узнаете

• Какой формулой задается вертикальная прямая?
• Сколько точек нужно, чтобы построить прямую?
• Как из прямых сделать гиперболу?

Любой процесс в этой жизни можно нарисовать. Это могут быть картины великих художников, которые запечатлели исторические события, или научные иллюстрации, чертежи, диаграммы и многое-многое другое. Даже сердечный ритм человека можно визуально изобразить с помощью кардиограммы. 

Математика не стала исключением. Любую математическую модель можно нарисовать, но для этого необходимо воспользоваться специальным инструментом – графиком функции. Разумеется, каждая модель будет выглядеть по-своему, но существует несколько функций, которые задают очень похожие фигуры. Их мы и рассмотрим в этой статье. 

Пара слов о функциях

При работе с функциями необходимо помнить про их основные свойства: область определения, область значений, нули функций, ее возрастание и убывание и многое-многое другое. Так что, если все эти нужные понятия ускользнули от вашего внимания, советуем сначала прочитать статью «Определение и график функции», а уже затем вернуться сюда. 

Также вспомним, что функция – это зависимость одной переменной от другой, а график функции – это представление данной зависимости на координатной плоскости. 

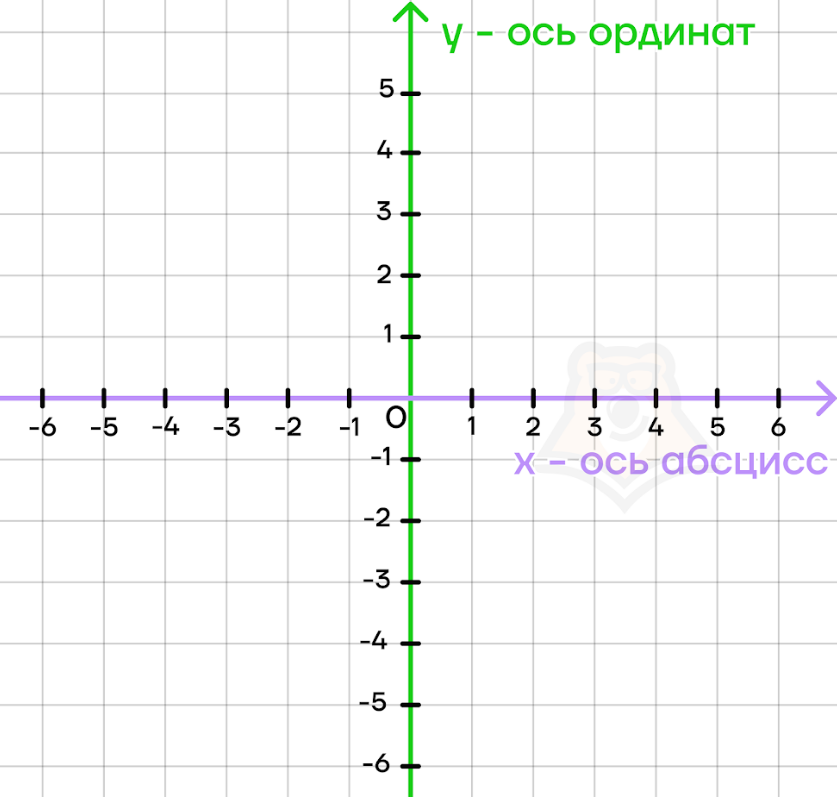
Чаще всего под координатной плоскостью подразумевают прямоугольную систему координат. 

Прямоугольная (декартова) система координат – система координат, состоящая из перпендикулярных осей, имеющих направление, начало отсчета и единичные отрезки. 

Оси можно назвать как угодно, но чаще это х – горизонтальная ось, и у – вертикальная ось. Также их называют ось абсцисс и ось ординат соответственно. 

А теперь перейдем к рассмотрению основных элементарных функций.

Элементарная функция – это функция вида y=f(x) , где f(x) – это формула, содержащая конечное число арифметических операций. 

Существует несколько основных элементарных функций. Чтобы начать рассматривать их, ответим на вопрос: что можно сделать с числом? Сложить, вычесть, умножить, разделить, возвести в степень, извлечь корень и другие операции. Но начнем с самого простого: мы не будем делать с числом ничего. 

Постоянная функция

Постоянная функция задается следующей формулой:

y=C

Здесь С – некоторое число. Вместо С можно подставить абсолютно любое число. 

Разберем функцию на примере y=3. Попробуем отметить несколько таких точек: 

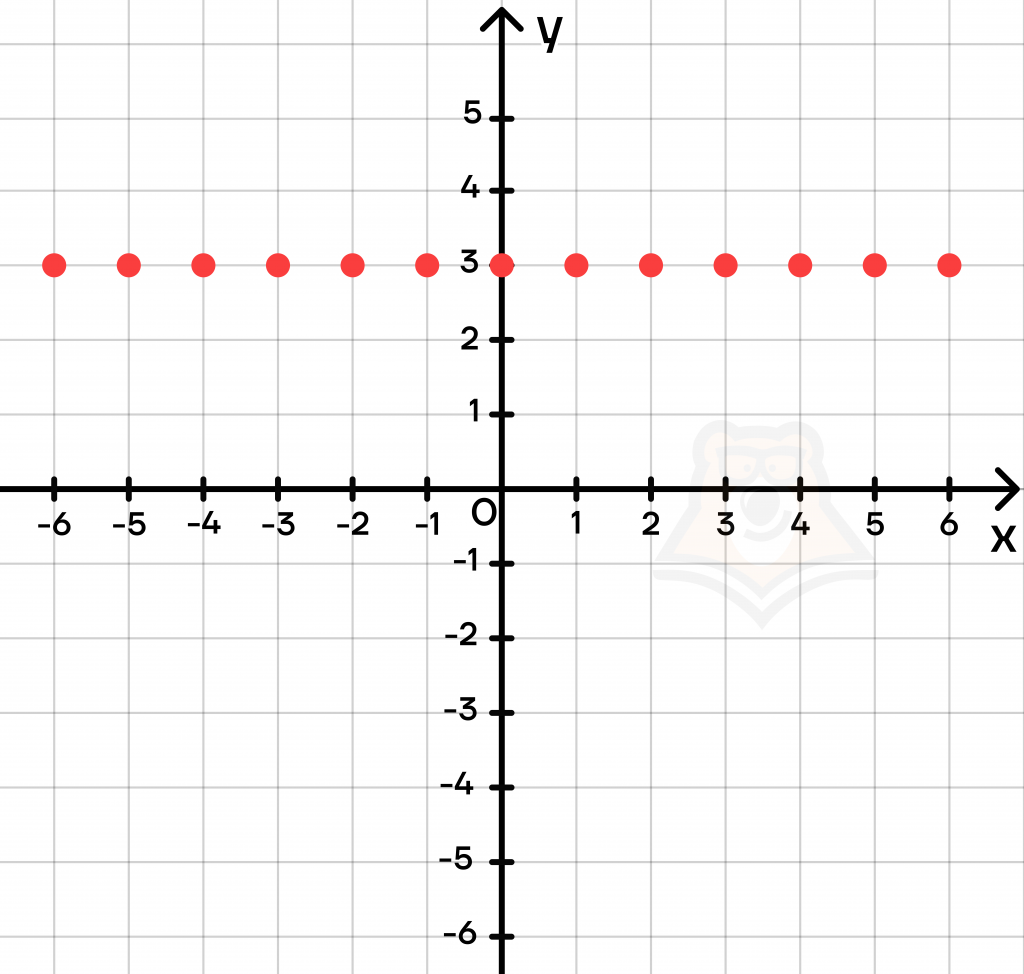
Между отмеченными нами точками все равно остаются точки, в которых у равен 3. Если мы попробуем отметить все-все такие точки, то получим горизонтальную прямую: 

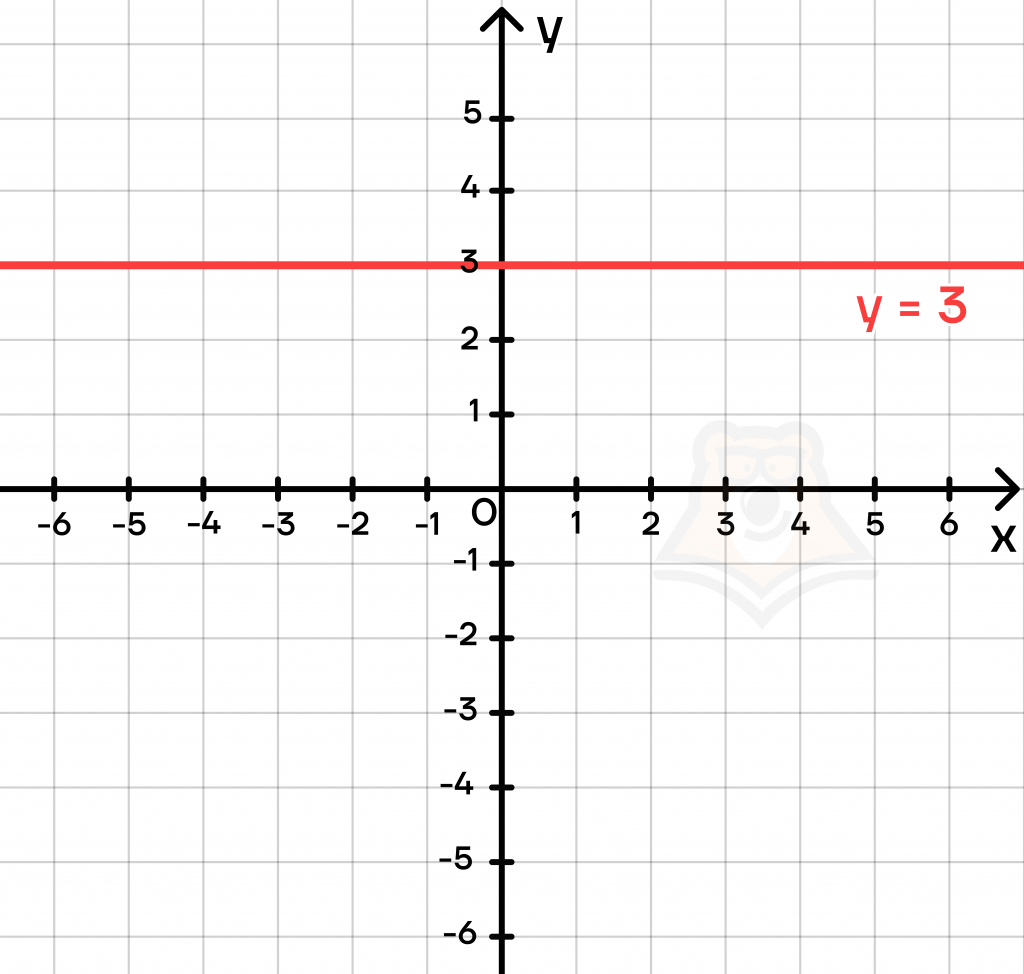
Она и будет графиком функции y=3. 

Если мы поменяем значение С, то линия просто сдвинется вверх или вниз. Важное условие: линия строго параллельна оси абсцисс, то есть оси х.

Разберем свойства такой функции. 

Свойства постоянной функции:

1. Область определения: \(D(y)=(-\infty;+\infty)\).
2. Область значений функции: E(y)={C}, то есть, то самое число, которое дано в условии функции.
3. Функция не возрастает и не убывает.
4. Функция непериодическая.

Какой формулой задается вертикальная прямая? Вертикальная прямая строится аналогично функции y=C, однако в этот раз мы должны учесть все значения х. Следовательно, нам понадобится функция x=C, где С – некоторое число. Например, графиком уравнения x=5 будет вертикальная прямая, проходящая через эту точку. Стоит заметить, что такие графики всегда будут строго параллельны оси ординат.

Заметим, что координатные оси тоже задаются функциями y=0 и x=0. 

Что же произойдет, если мы начнем как-то менять число? Попробуем произвести над некоторым числом обычные арифметические операции: сложение, умножение, вычитание и деление. В этом случае мы получим линейную функцию.

Линейная функция

Если до этого в функции ничего не менялось, то сейчас нам предстоит столкнуться с понятием переменная. 

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.

Как мы уже говорили, функция – это зависимость одной переменной (y) от другой (x). Чтобы отследить изменения зависимой переменной, необходимо менять значения у переменной х. Следовательно, когда мы будем производить операции над х, то будем подразумевать, что вместо него можно подставить любое число. 

Вернемся к линейной функции. 

Линейная функция – это функция вида y=kx+b, где k и b – известные числа, графиком которой является прямая.

y=kx+b, где k – коэффициент; b – свободный член; x – переменная.

Может показаться, что это очень оторванная от реальности математическая модель, однако это не так. Например, с линейной функцией мы встречаемся, когда оплачиваем проезд в общественном транспорте.

Коэффициент и переменная определяют стоимость билета в зависимости от дальности поездки. Свободным членом может выступать доплата за комфортное место или за поезд-экспресс.

Пусть х – километры, которые нам нужно проехать. 

Дальность маршрута	Менее 200 км	200—300 км	Более 300 км
Цена поездки в обычном вагоне за 1 км (k)	15 руб.	10 руб.	5 руб.
Доплата за вагон «Люкс» (b)	750 руб.	1000 руб.	1250 руб.

Так, если мы хотим проехать 233 километра в вагоне Люкс, нам придется заплатить:
y=kx+b=10*233+1000=3330 рублей. 

Но вернемся к математике. Рассмотрим пример линейной функции и ее график:

y=2x+3

Составим таблицу значений. Для этого нужно подставить любой х и найти значение у. Например, если x=-3, то y=2*(-3)+3=-6+3=-3. 

x	-3	-2	-1	0	1
y	-3	-1	1	3	5

Сколько точек нужно, чтобы построить прямую? Для построения прямой, на самом деле, достаточно всего две точки. Это говорится в одной из аксиом геометрии: через любые две точки проходит единственная прямая. Подробнее про эту и другие аксиомы геометрии можно узнать в статье «Основы планиметрии».

Мы же нашли пять точек и проделали лишнюю работу. Возьмем точки (-1;1) и (0;3) и построим график функции:

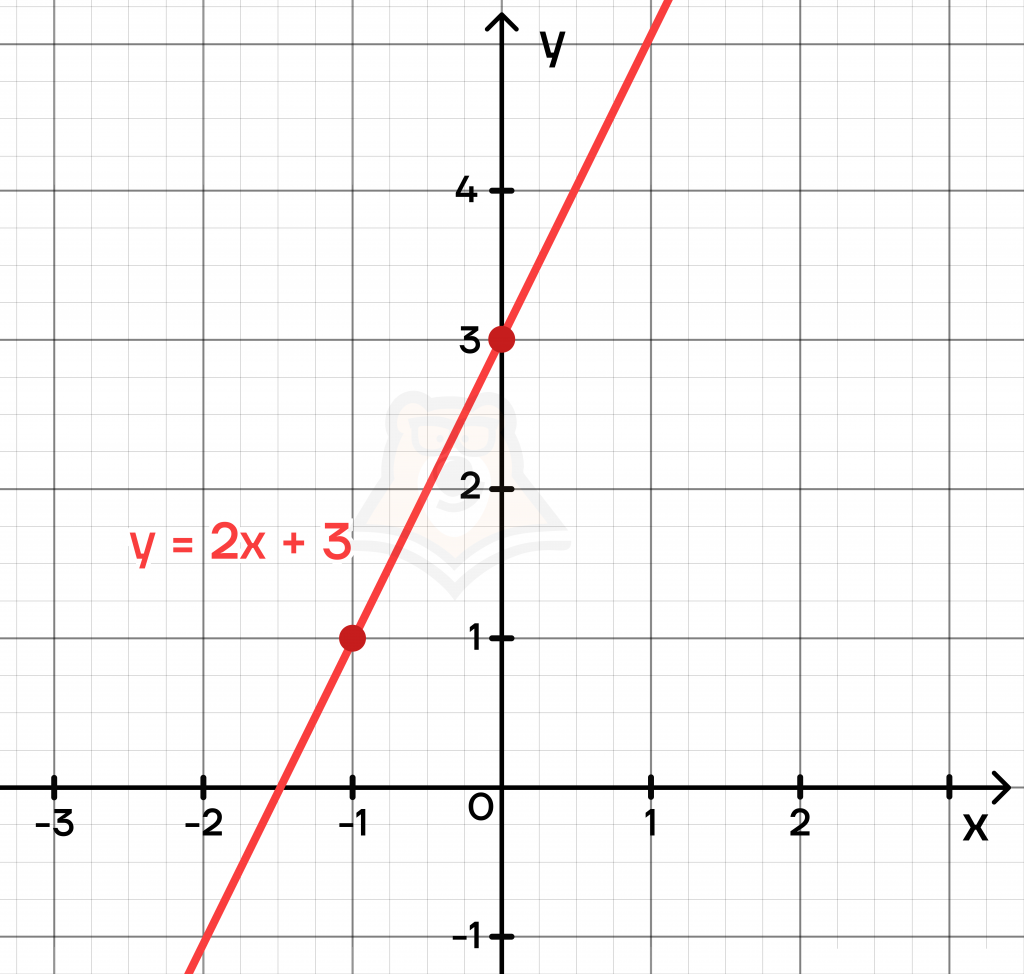
Полученный нами график является графиком линейной функции.

Также можно составить уравнение линейной функции самостоятельно при наличии графика. Рассмотрим решение такой задачи. 

Такое задание может встретиться в ЕГЭ по профильной математике в №10. 

На рисунке изображен график функции f(x)=kx+b. Найдите f(-10). 

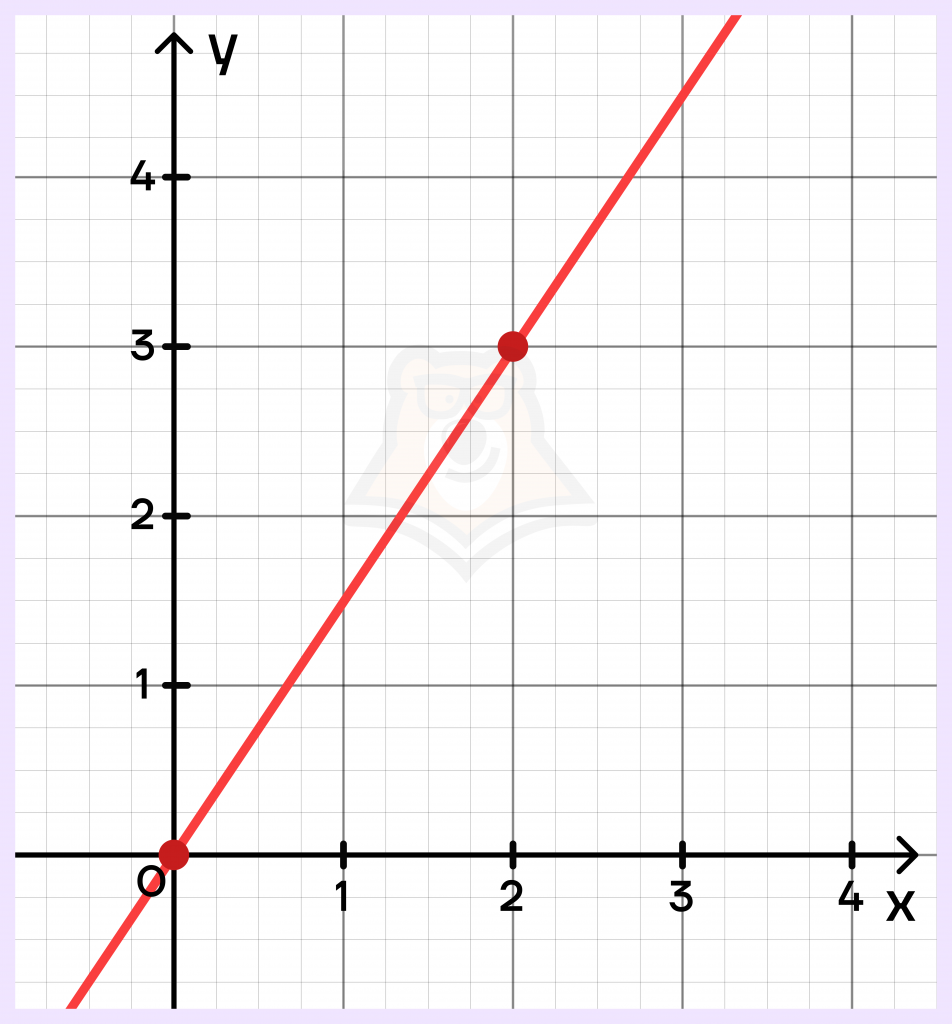
Решение.
Заметим, что записи f(x)=kx+b и y=kx+b – одно и то же. Поэтому вместо f(x) мы можем смело использовать y. 

Подпишем на графике отмеченные точки: 

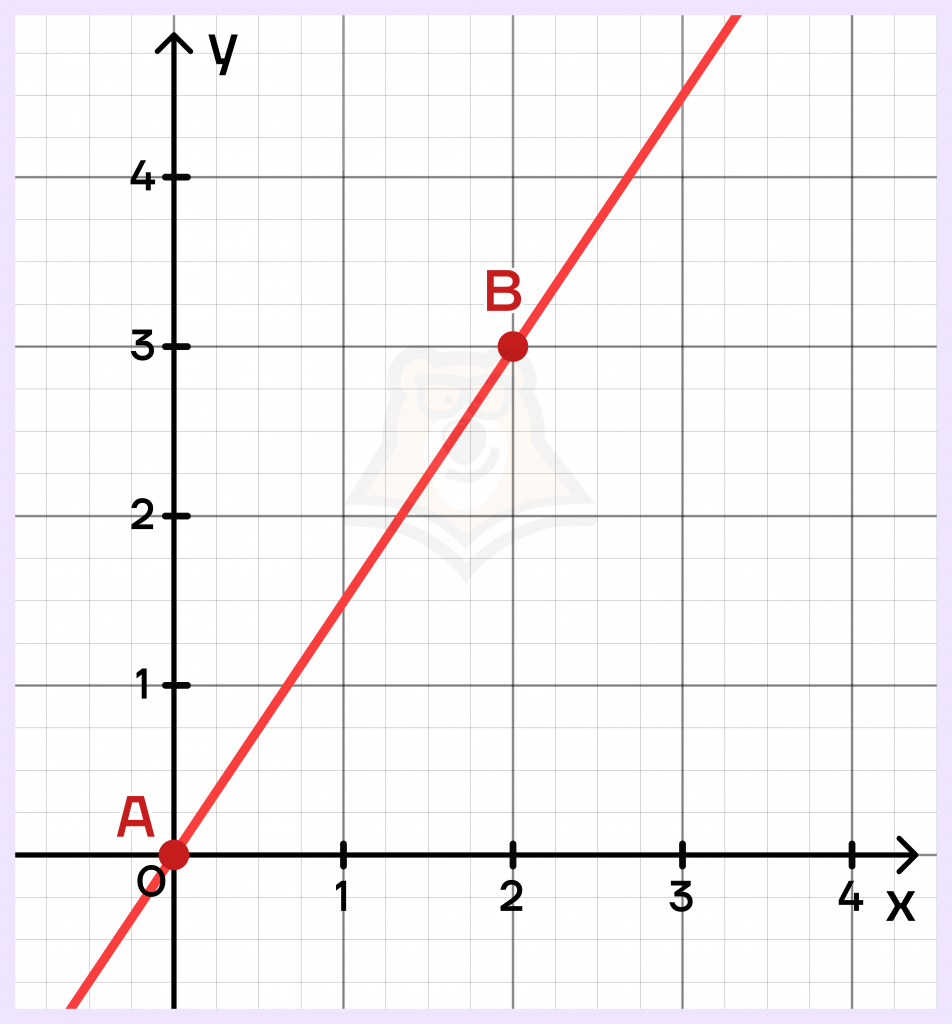
Получаем точки A(0;0) и B(2;3). Подставим точку А в уравнение прямой:
y=kx+b
0=k*0+b
b=0

Теперь, зная коэффициент b, мы можем найти k с помощью точки В:
y=kx+0
3=k*2
\(k=\frac{3}{2}=1,5\)

Таким образом, мы получили функцию y=1,5x. 

Осталось найти f(-10), то есть значение функции при x=-10. Подставляем:

y=1,5*(-10)=-15

Ответ: – 15

Если посмотреть на две предыдущие функции, то можно заметить, что в зависимости от коэффициентов меняется и график функции. За что же отвечают коэффициенты k и b?

Коэффициенты линейной функции 

Начнем с коэффициента b. Для этого построим три графика:

1. y=x
2. y=x+1
3. y=x-1

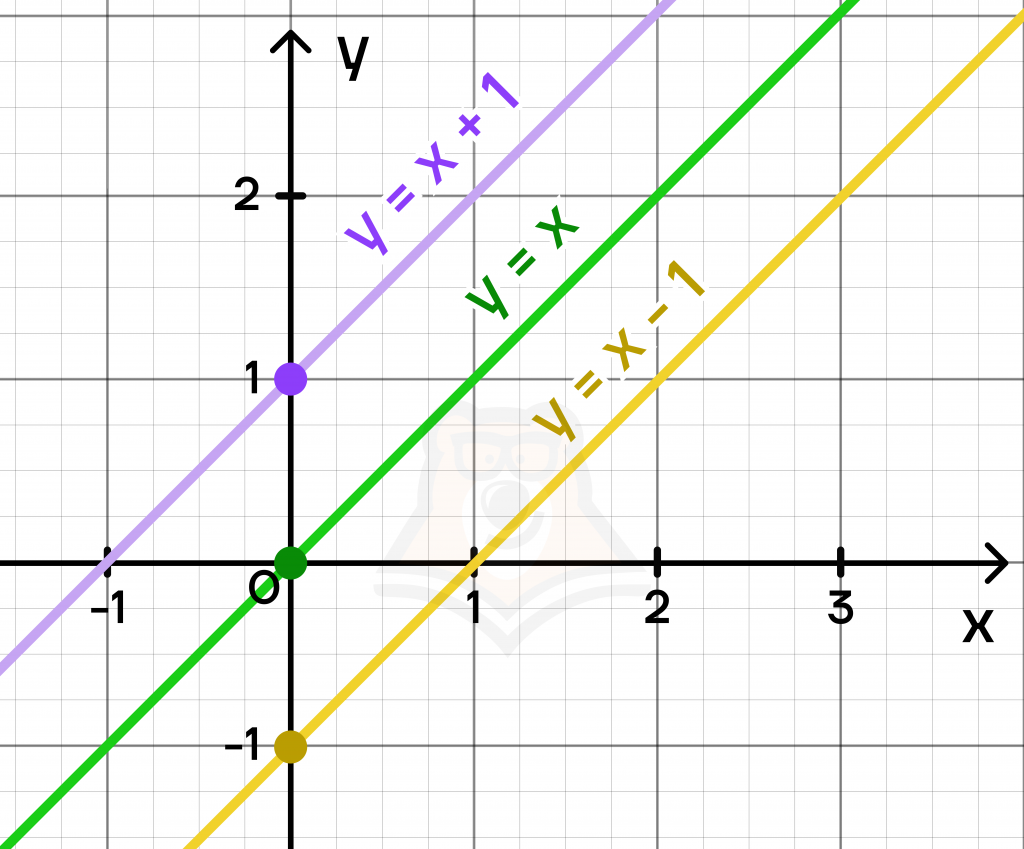
Заметим, что наклон у графиков не меняется. Единственное их отличие: они двигаются вдоль оси y. Это можно сравнить с передвижением ползунка вверх-вниз. 

Обратим внимание на точки пересечения графиков с осью ординат. Они соответствуют коэффициенту b. Например, для функции y=x+1 точка пересечения с осью у равен 1, как и коэффициент b=1. 

В случае с функцией y=x коэффициента b нет, а значит, b=0. Точка пересечения с осью ординат тоже равна 0. Сделаем вывод. 

Коэффициент b – это длина отрезка по оси OY, на который происходит сдвиг от начала координат. Коэффициент может быть отрицательным, если график пересекается с осью Y в точке с отрицательным значением.

Итак, коэффициент b отвечает за движение графика вдоль оси ординат. За что отвечает коэффициент k? 

Коэффициент k – это тангенс угла наклона прямой к оси х, который равен отношению \(\frac{\Delta y}{\Delta x}\) двух произвольных точек. 

Важно заметить: угол наклона всегда определяется между графиком прямой и положительным направлением оси х.

И снова тригонометрия! Вспомним, что тангенс – это отношение противолежащего катета к прилежащему. Подробнее про тригонометрические функции вы можете прочесть в статье «Тригонометрическая окружность. Часть 1». 

Рассмотрим график функции y=x. Отметим точки A(0;0) и B(1;1), а также построим через них прямоугольный треугольник. 

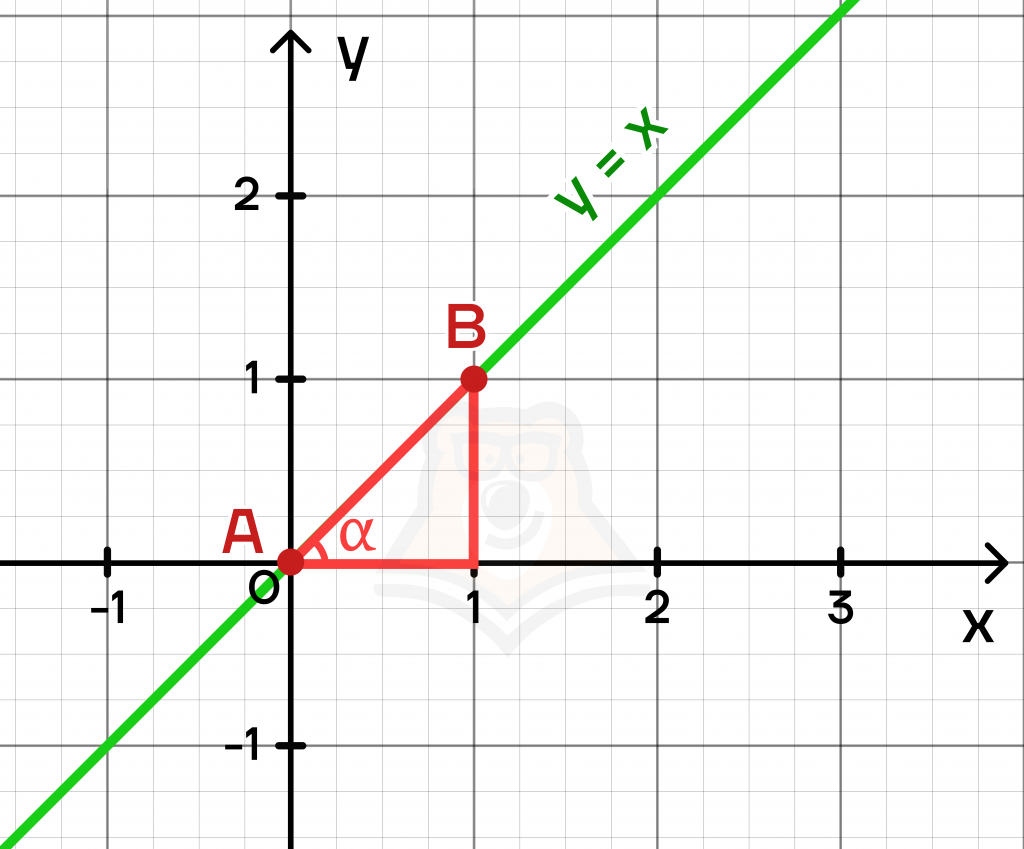
Выразим координаты точек через переменные: \(A(x_1;y_1), B(x_2;y_2)\). По определению переменной найдем значение k: 

\(k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}=\frac{1-0}{1-0}=1\)

Следовательно, \(tg\alpha =1\), а сам угол будет равен 45°. Перевод из тангенсов в углы можно совершать с помощью таблицы, о которой вы можете узнать в статье «Формулы тригонометрии и простейшие уравнения». 

Попробуем увеличить угол на графике и найти значение k. В этом случае A(0;0) и B(1;3).

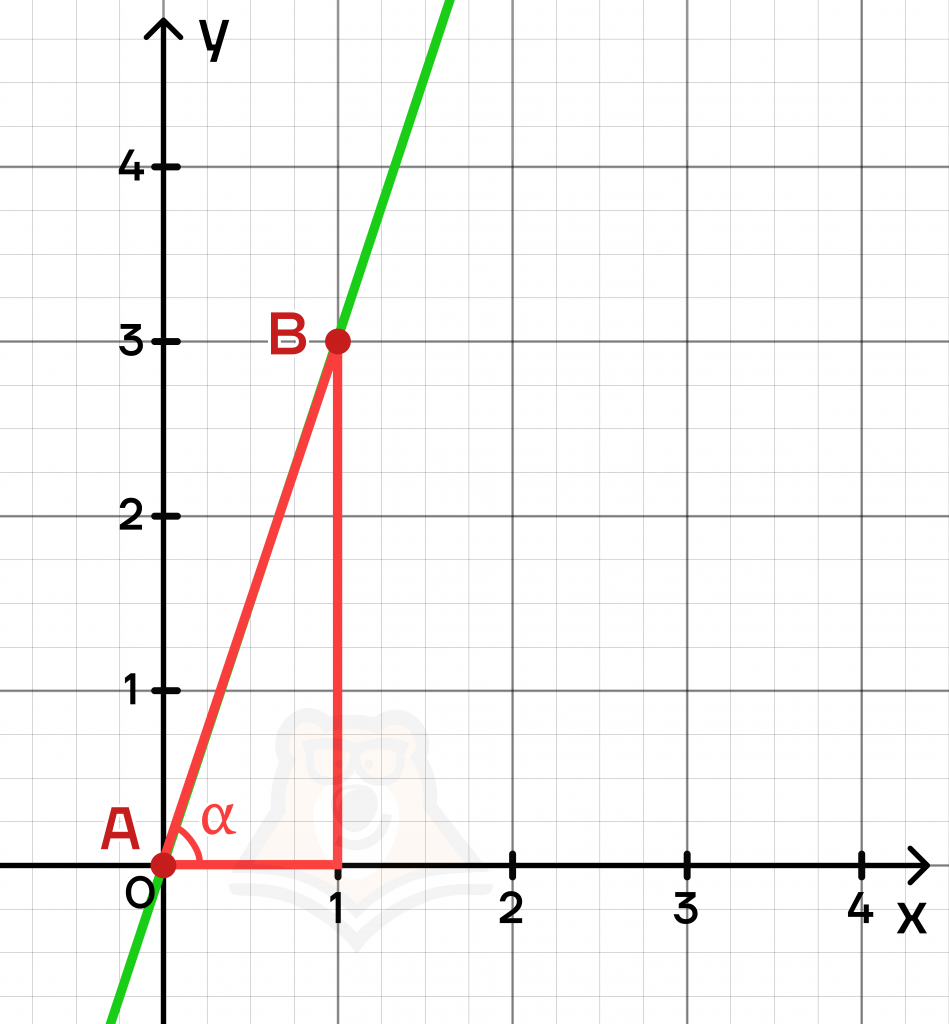
Получаем: 

\(k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}=\frac{3-0}{1-0}=3\)

Следовательно, перед нами график \(y=3x\). 

А вот если мы уменьшим коэффициент k, то угол на графике наоборот уменьшится. Например, так выглядит график \(y=0,5x\):

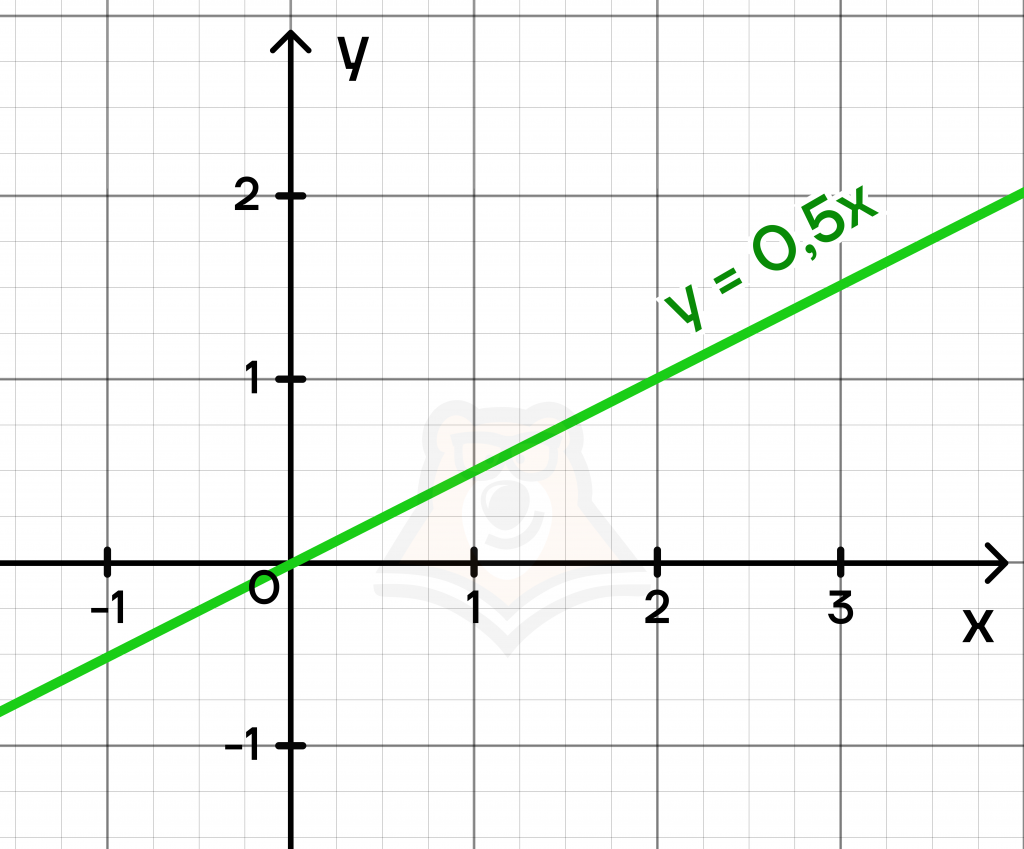
Если мы наложим три графика на одну координатную плоскость, то заметим закономерность: чем больше коэффициент k, тем больше угол наклона графика относительно оси x. 

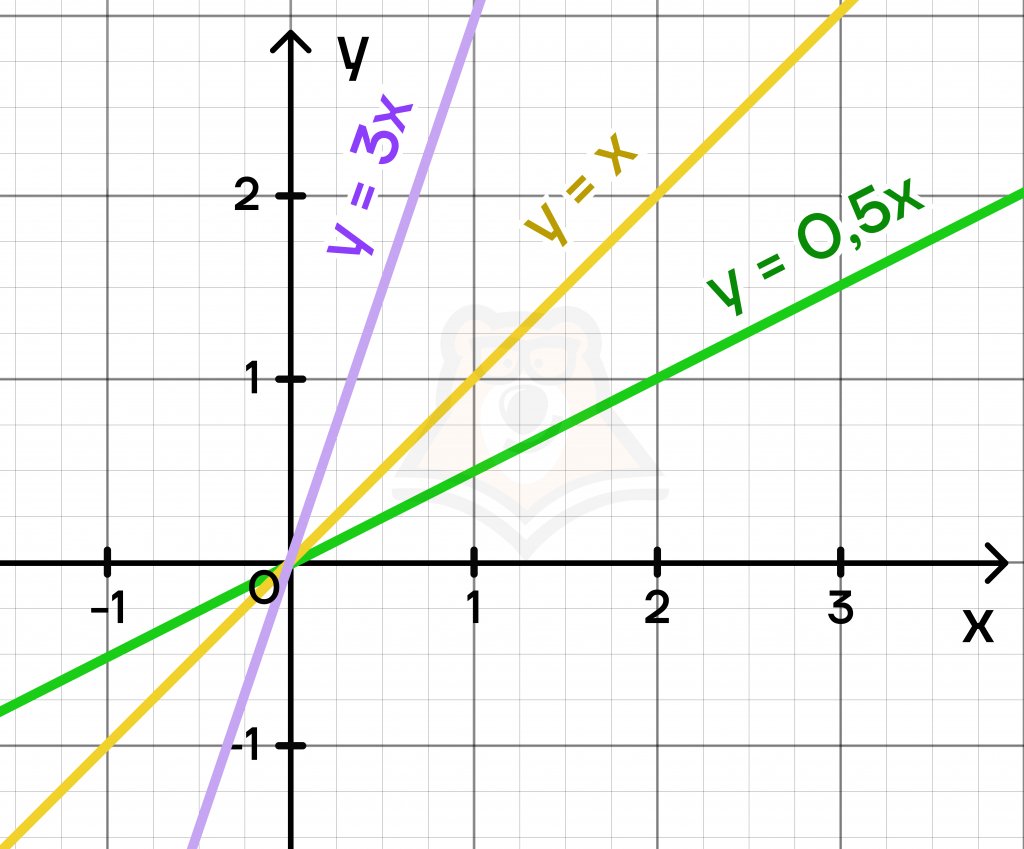
Если сравнивать с горками (теми самыми, с которых можно кататься на санках или сноуборде), то чем больше коэффициент, тем «круче» горка. 

До этого мы рассматривали только возрастающие функции. А что делать с убывающими?

Допустим, мы знаем, что угол наклона функции 135 градусов. Тогда смежный ей угол будет равен: \(180-135=45\) градусов. Так будет выглядеть ее график: 

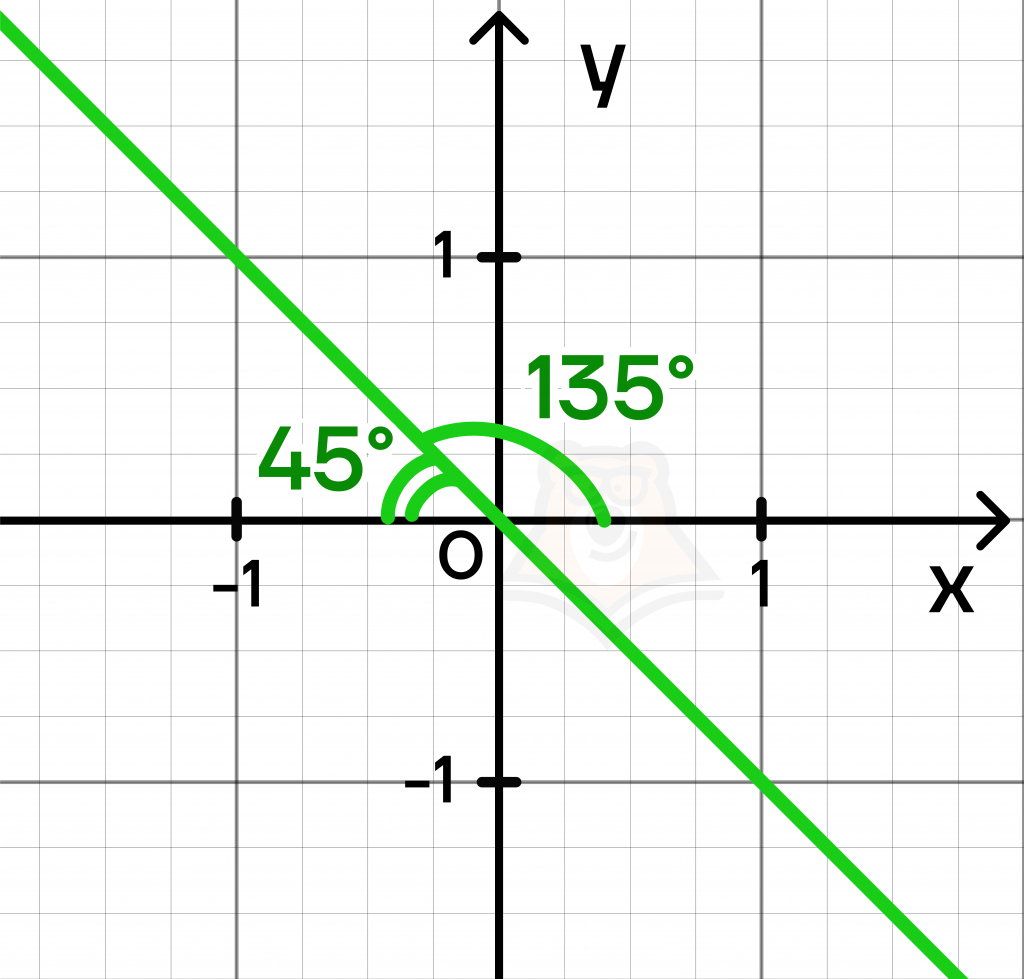
Мы уже знаем, что для угла 45° k=1. Воспользуемся формулой приведения: 

\(tg 135=tg(180-45)=-tg 45=-1\)

Следовательно, для данного графика \(k=-1\), а функция имеет вид \(y=-x\). 

Все убывающие функции имеют отрицательный коэффициент k. 

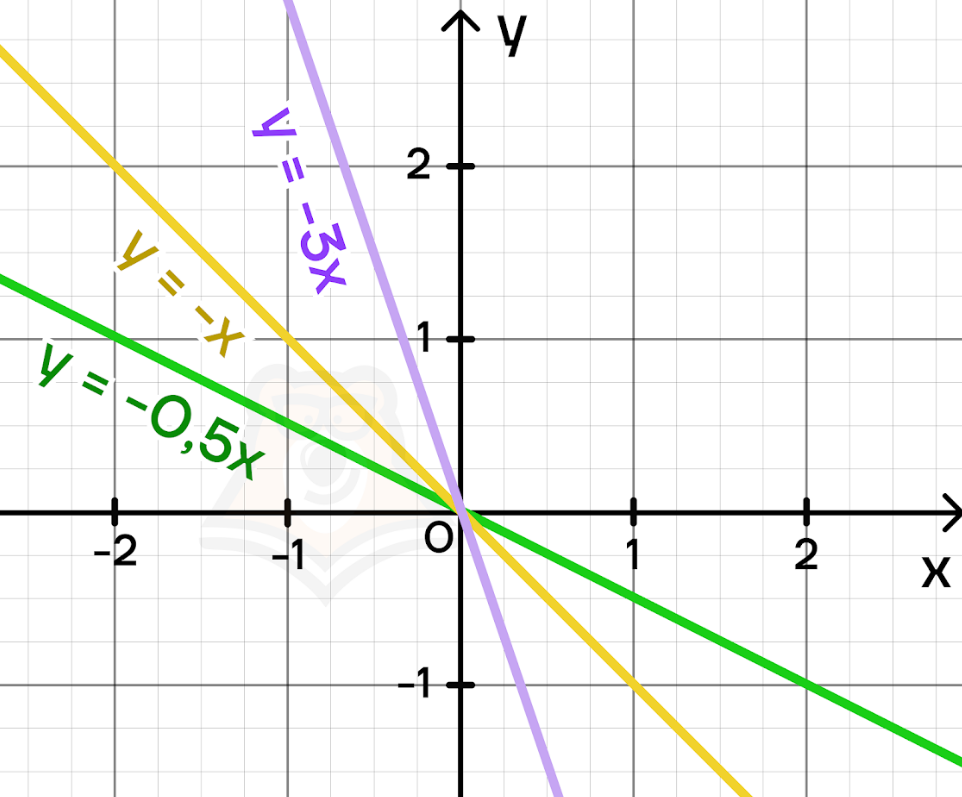
Если мы сравним графики с горками, то заметим, что чем меньше коэффициент, тем «круче» горка. 

Подведем итог и определим основные свойства линейной функции. 

Свойства линейной функции:

1. Область определения: \(D(y)=(-∞;+∞)\).
2. Область значений функции: \(E(y)=(-∞;+∞)\).
3. Наименьшего и наибольшего значения не существует.
4. Непериодическая.
5. Возрастает при \(k>0\), убывает при \(k<0\).

Есть еще одно арифметическое действие, которое важно рассмотреть: деление. Однако делить мы будем не на коэффициент, а на переменную. Какой график получится в этом случае? 

Функция обратной пропорциональности

Функция обратной пропорциональности – это функция вида \(y=\frac{k}{x}\), где k – известное число и \(k≠0\), графиком которой является гипербола.

\(y=\frac{k}{x}\), где  \(k\) – известное число, \(k≠0\); \(x\) – переменная.

Почему k не может быть равно 0? Все просто: тогда мы перейдем к постоянной функции \(y=0\) (если ноль разделить на любое число, кроме нуля, то получится 0). 

Важно заметить, что переменная должна быть в знаменателе, иначе перед нами будет не функция обратной пропорциональности. Например, функция \(y=\frac{x}{2}\) – линейная функция, которую можно записать в виде \(y=\frac{1}{2}*x\). А вот функция \(y=\frac{2}{x}\) – это функция обратной пропорциональности. 

Рассмотрим пример такой функции \(y=\frac{2}{x}\). В этом случае нам понадобится больше, чем 2 точки, поскольку сам график уже будет представлять не прямую. 

Составим таблицу, отметим точки на графике и соединим их плавной линией.

x	1	2	4	-1	-2	-4
y	2	1	\(\frac{1}{2}\)	-2	-1	\(-\frac{1}{2}\)

 У нас получится две «дуги». Такая фигура называется гиперболой. 

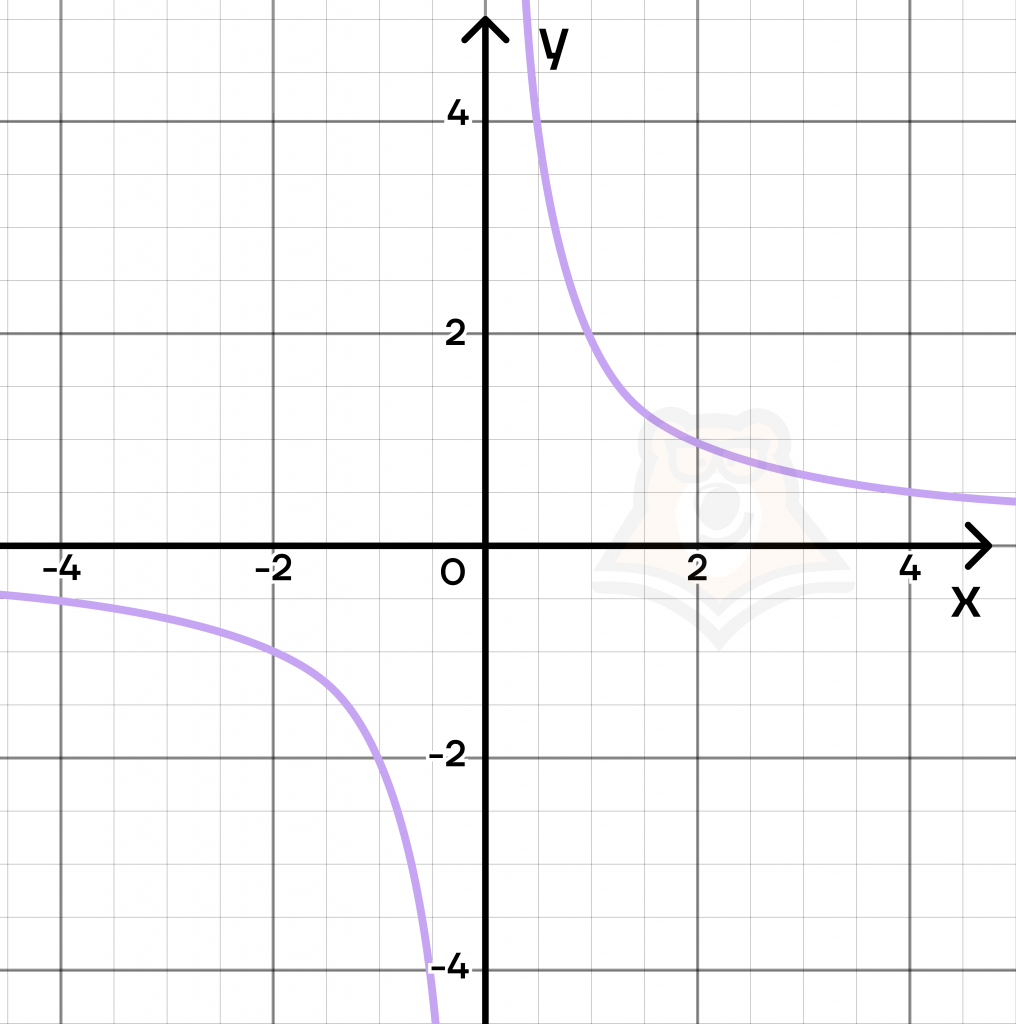
Что мы можем сказать про гиперболу? Она всегда будет стремиться к осям абсцисс и ординат, но никогда не пересечет их, поскольку оси являются асимптотами. 

Асимптота – прямая, к которой неограниченно близко приближается график функции, но никогда ее не пересекает. 

Асимптоты появляются из-за ограничений. Вспомним, что ограничения – это те значения, при которых существует выражение. Иногда их называют ОДЗ. 

Для гиперболы будут следующие ограничения: \(x\neq 0, y\neq 0\). 

Почему \(y\neq 0\) мы уже разобрали – функция превратится в постоянную. А вот \(x\neq 0\), поскольку стоит в знаменателе, а на 0 делить нельзя. Так и получаем ограничения, или асимптоты: \(x\neq 0, y\neq 0\). 

У гиперболы тоже появляется коэффициент k. Как он влияет на расположение гиперболы?

Для начала немного отвлечемся на четверти координатной плоскости. Если координатная плоскость – прямоугольник, то оси делят ее на 4 прямоугольника меньше. Каждый такой прямоугольник имеет свой номер и называется четверть. Отсчет идет с верхнего правого прямоугольника против часовой стрелки: 

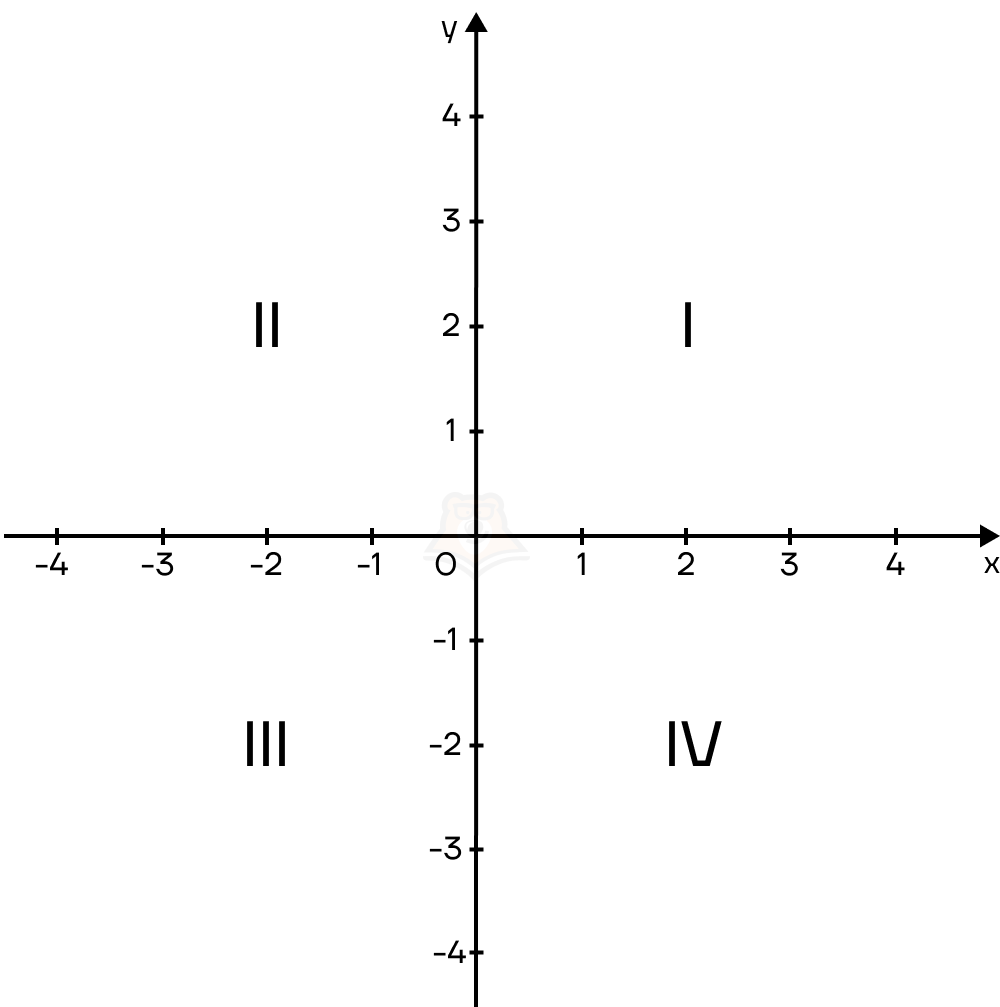
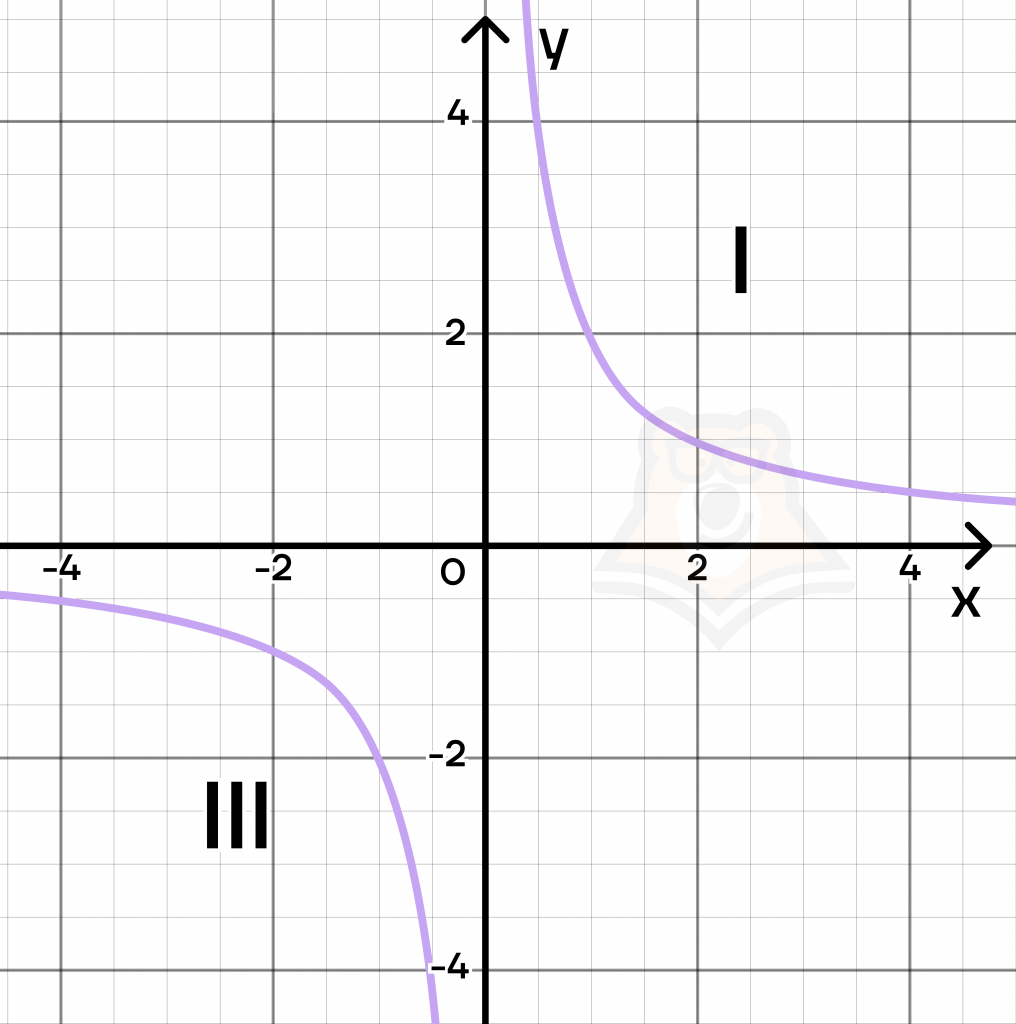
Итак, коэффициент k может принимать либо положительные, либо отрицательные значения. В случае положительных значений, ветви гиперболы будут лежать в первой и третьей четвертях (то есть в четвертях, где обе координаты либо положительны, либо отрицательны). 

Это легко выводится: если мы разделим положительное число на положительное, то получим положительное. Следовательно, \(x>0, y>0\) – I четверть. 

Пусть нам будет дана функция \(y=\frac{2}{x}\), тогда подставив \(x=1\) получаем: \(y=\frac{2}{1}=2\). 

А вот если разделим положительное число на отрицательное, то получим уже отрицательное число. Следовательно, \(x<0, y<0\) – III четверть. 

Теперь подставим в данную нам функцию \(x=-1\), получаем: \(y=\frac{2}{-1}=-2\). 

Таким образом, мы получаем следующее. Гипербола при \(k >0\) лежит в первой и третьей четвертях.

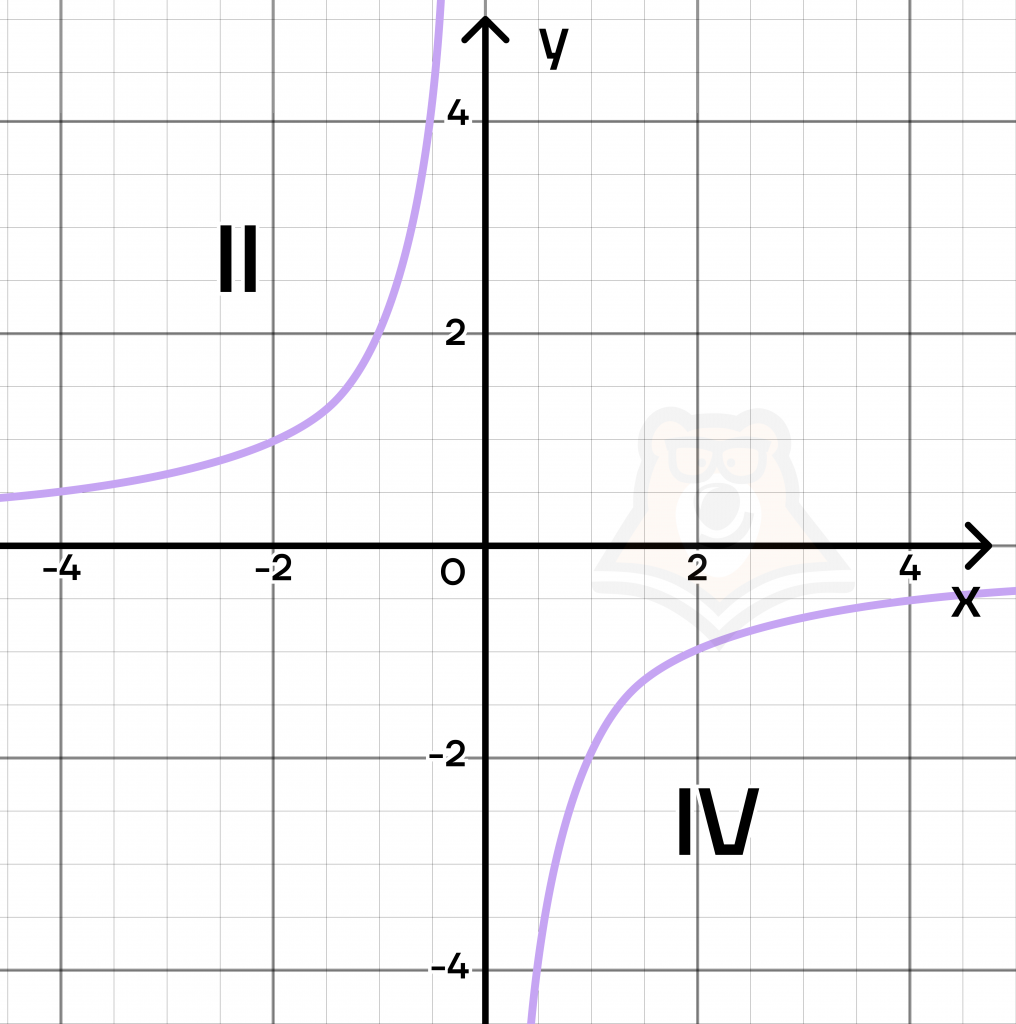
Аналогичными рассуждениями можно проверить случай, когда \(k<0\). Пусть в этот раз нам будет дана функция \(y=\frac{-2}{x}\). 

• Если разделим отрицательное число на положительное, то получим отрицательное число. Следовательно, \(x>0, y<0\) – IV четверть. 
  Например, \(x=1 =>y=\frac{-2}{1}=-2\).

• Если разделим отрицательное число на отрицательное число, то получим положительное число. Следовательно, \(x<0, y>0\) – II четверть.
  Например, \(x=-1 => y=\frac{-2}{-1}=2\). 

А вот если \(k< 0\), то гипербола лежит во второй и четвертой четвертях.

В линейной функции был коэффициент, отвечающий за сдвиг прямой вдоль оси у. Может ли также двигаться гипербола? Да! Более того, она может двигаться вдоль двух осей: гипербола может также двигаться и по оси х, и по оси у.

Движение графика по оси Y

Чтобы сдвинуть гиперболу, нам нужно немного поменять ее асимптоту: она теперь не должна будет совпадать с осью х. Для этого необходимо поднять или опустить все ее точки на одинаковое расстояние, то есть прибавить к ним коэффициент n. 

\(y=\frac{k}{x}+n\)

При \(n < 0\), сдвиг вниз. 

При \(n > 0\), сдвиг вверх.

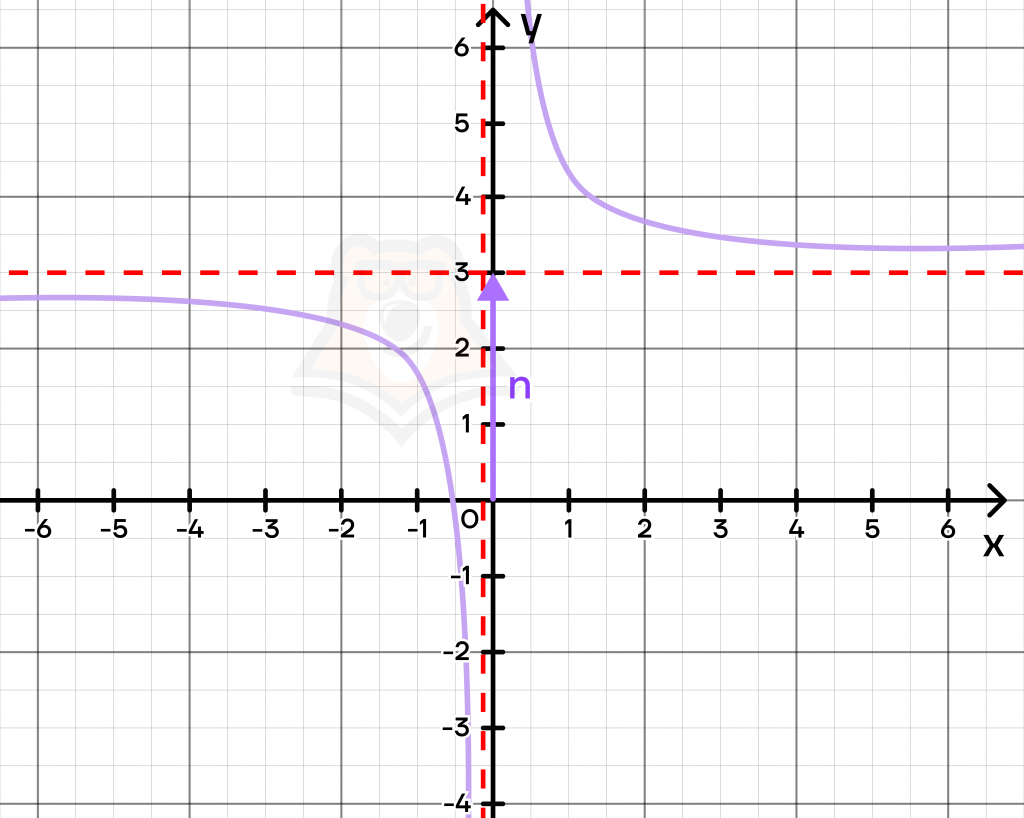
По графику выше можно сделать вывод, что \(n = 3\), поскольку асимптота сдвинута на 3 единицы вверх. 

С движением вдоль оси х все несколько сложнее. 

Движение графика по оси X

Чтобы сдвинуть асимптоту вправо или влево, нужно изменить значения абсциссы. Для этого мы уже прибавляем/вычитаем значения не ко всей точке, а только к х. Тогда функция принимает вид: 

\(y=\frac{k}{x + c}\) 

При \(c < 0\), сдвиг вправо. 

При \(c > 0\), сдвиг влево. 

Следовательно, если мы прибавляем число, гипербола двигается в отрицательное направление. И наоборот, если мы вычитаем число, то гипербола двигается в положительном направлении. 

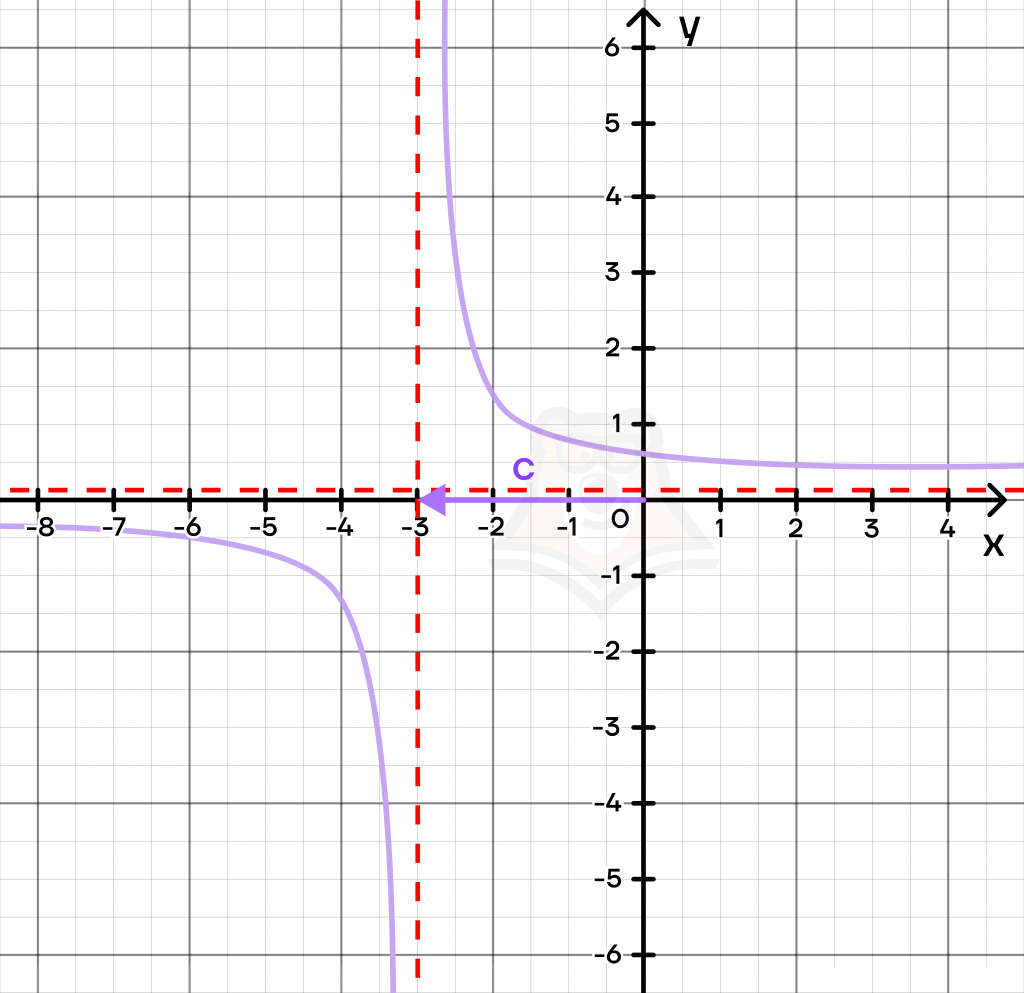
По графику выше можно сделать вывод, что \(c = 3\).

Итак, какие свойства мы можем выделить у гиперболы?

Свойства функции обратной пропорциональности:

1. Область определения: \(D(y)=(-∞;0)\cup (0;+∞)\)
2. Область значений функции: \(E(y)=(-∞;0)\cup(0;+∞)\)
3. Наименьшего и наибольшего значений не существует.
4. Непериодическая.
5. При \(k > 0\) убывает на промежутке \((-∞;0)\) и \((0;+∞)\).
   При \(k < 0\) возрастает на промежутке \((-∞;0)\) и \((0;+∞)\).
6. Нулей нет.
7. Нечетная.

Как из прямых сделать гиперболу? Математика и архитектура неразрывно связаны. Так, в архитектуре существует целый ряд построек, выполненных из прямых стержней, но при этом имеющих форму гиперболы. Такие конструкции образовываются с помощью пересекающихся прямых, причем каждая прямая принадлежит плоскости. В результате получается изогнутая поверхность, которая называется гиперболоидом. Первым гиперболоидную форму конструкций ввел в архитектуру В.Г. Шухов. Примером гиперболоида может быть Сиднейская телебашня.

Где в реальной жизни мы можем встретить эту функцию? Самый простой пример – движение автомобиля: чем выше его скорость, тем меньше времени потребуется, чтобы преодолеть одно и то же расстояние.

Однако примеры гиперболы могут встретиться и при других условиях. Рассмотрим такой пример из №3 ЕГЭ по базовой математике. 

Мощность обогрева в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая регулятор, установленный в салоне. При этом меняется сила тока в электрической цепи электродвигателя  — чем меньше сопротивление, тем больше сила тока. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в Омах), на оси ординат  — сила тока (в Амперах). На сколько изменится сила тока, если сопротивление уменьшится с 10 до 4 Ом?

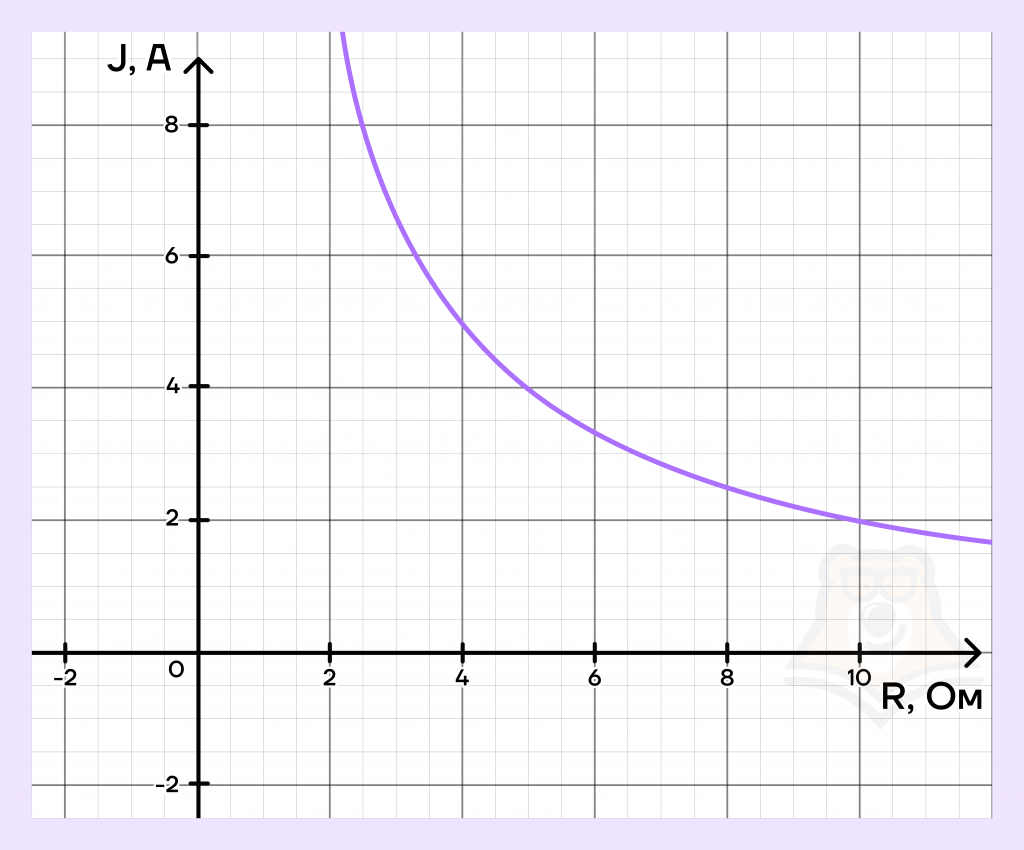
Решение. Найдем на графике значение силы тока при сопротивлении 10 и 4 Ом. 

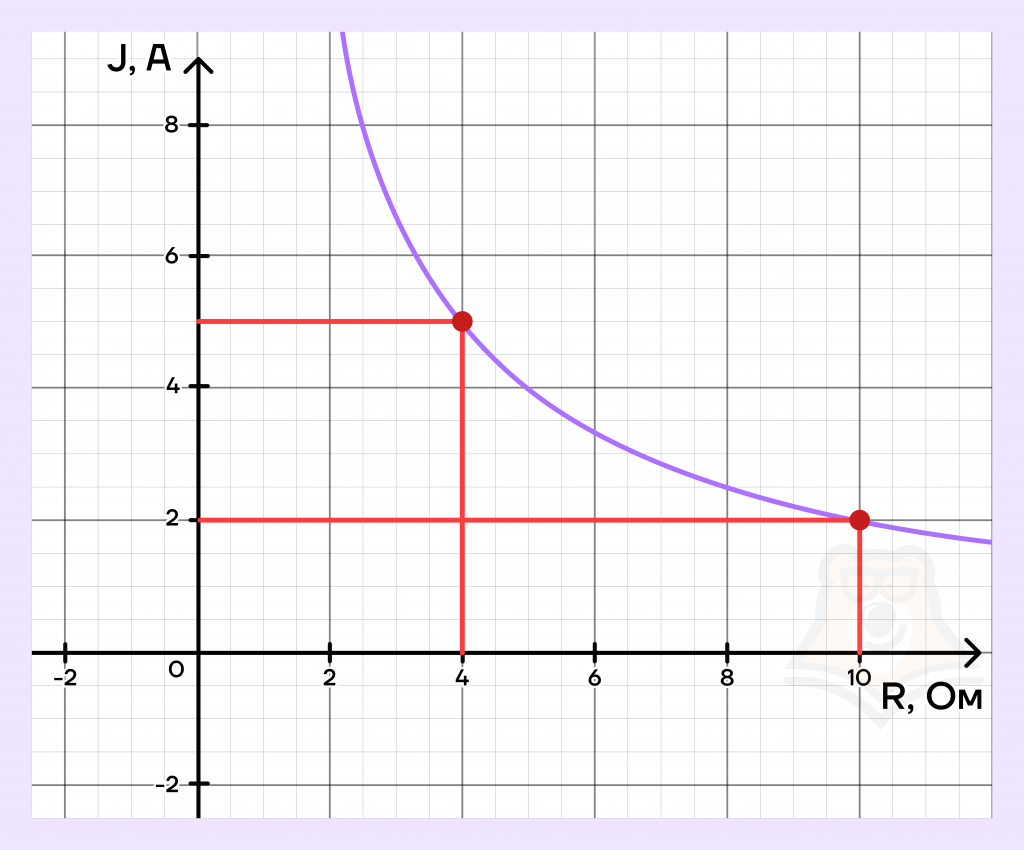
Тогда для R=10 получаем I=2, а для R=4 получаем I=5. Следовательно, сила тока изменилась на:

5-2=3 А

Ответ: 3

Мы начали разбор основных видов функций и уже узнали про три из них. Однако, на этом рано останавливаться, впереди нас ждет еще несколько более сложных и увлекательных функций, прочитать про которые вы можете в статье «Основные элементарные функции. Часть 2». 

Термины

Возрастающая функция — такая функция, для любой пары аргументов х₁ и х₂ (х₁ < х₂) которой выполняется неравенство f(x₁) < f(x₂). 

Нули функции — это значение аргумента х, при котором значение функции равно 0.

Область значений функции — это все значения, которые может принимать функция. Область значений обозначается как Е(у). 

Область определения функции — это все допустимые значения аргумента функции (то есть х), при которых функция будет определена. Область определения обозначается как D(y). 

Периодическая функция — это такая функция, для любого значения аргумента из области определения которой выполняется условие f(x)=f(x+T), где Т — период функции, отличный от 0. 

Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 180°. Подробнее про виды углов вы можете узнать в статье «Основы планиметрии». 

Убывающая функция — такая функция, для любой пары аргументов х₁ и х₂ (х₁ < х₂) которой выполняется неравенство f(x₂) < f(x₁). 

Четной функцией называется такая функция, график которой симметричен относительно оси Оу.

Фактчек

• Любую функцию можно изобразить графически и определить ее основные свойства. Однако существует несколько видов функций, графики и свойства которых очень похожи. 
• Для построения графиков пользуются прямоугольной системой координат. Прямоугольная (декартова) система координат – система координат, состоящая из перпендикулярных осей, имеющих направление, начала отсчета и единичные отрезки. 
• Постоянная функция задается формулой \(y=C\) и является горизонтальной прямой. Такая функция имеет следующие свойства: область определения \(D(y)=(-\infty;+\infty)\), область значений функции E(y)={C}, функция не возрастает и не убывает, функция непериодическая.
• Линейная функция – это функция вида \(y=kx+b\), где k и b – известные числа, графиком которой является наклонная прямая. Коэффициент k отвечает за угол наклона прямой, коэффициент b за ее сдвиг вдоль оси у. Свойства линейной функции: область определения \(D(y)=-∞;+∞\), область значений функции \(E(y)=-∞;+∞\), наименьшего и наибольшего значения не существует, непериодическая, возрастает при \(k>0\), убывает при \(k<0\).
• Функция обратной пропорциональности – это функция вида \(y=\frac{k}{x}\), где k – известное число и \(k\neq 0\), графиком которой является гипербола. Функция имеет асимптоты \(x\neq 0, y\neq 0\). Ее свойства: область определения \(D(y)=(-∞;0)\cup(0;+∞)\), область значений функции \(E(y)=(-∞;0)\cup(0;+∞)\), наименьшего и наибольшего значений не существует, непериодическая, при \(k > 0\) убывает на \((-∞;0)\) и \((0;+∞)\), при \(k < 0\) возрастает на \((-∞;0)\) и \((0;+∞)\), нулей нет, нечетная.

Проверь себя

Задание 1.
Определите, какая из функций является линейной:

1. \(y=2x^2+\frac{1}{2}\)
2. \(y=\sqrt{x+2}\)
3. \(y=\frac{1}{2}x+3\)
4. \(y=\frac{1}{x-2}\)

Задание 2.
Выберите верное утверждение для функции \(y=x+3\):

1. График функции сдвинут влево на 3 единицы.
2. График функции сдвинут вниз на 3 единицы.
3. График функции сдвинут вправо на 3 единицы.
4. График функции сдвинут вверх на 3 единицы. 

Задание 3.
Определите какая функция является обратной пропорциональностью:

1. \(y=\frac{x}{2}+5\)
2. \(y=\frac{1}{x+2}\)
3. \(y=\sqrt{x+1}\)
4. \(y=x^2\)

Задание 4.
Выберите верное утверждение для функции \(y=\frac{3}{x-5}\):

1. График функции сдвинут вправо на 3 единицы.
2. График функции сдвинут вправо на 5 единиц.
3. График функции сдвинут влево на 3 единицы.
4. График функции сдвинут влево на 5 единиц. 

Задание 5.
Выберите верное утверждение для функции \(y=6\): 

1. Графиком является вертикальная прямая.
2. Графиком является горизонтальная прямая.
3. Область определения \(D(y)=6\).
4. Функция нечетная. 

Ответы:1. – 3; 2. – 4; 3. – 2; 4. – 2; 5. – 2.