Производная в задачах с параметром

На этой странице вы узнаете

• Как функция отражается в зеркале?
• Как не запутаться в точках минимума и максимума при расстановке знаков на прямой?
• Может ли касательная к функции пересекать ее в другой точке?

Что может рассказать о себе функция и как раскрыть ее секреты? Как узнать поведение функции, не видя ее график? Подробнее об этом в статье. 

Производная в задачах с параметром

С помощью производной можно многое сказать о функции: где она возрастает или убывает, какие точки экстремума у нее есть, можно даже найти касательную к функции. Поэтому перед прочтением статьи рекомендуем ознакомиться с понятиями «Производная» и «Исследование функции с помощью производной». 

Вспомним несколько важных фактов, которые относятся к производной:

• производная положительна на участках возрастания функции;
• производная отрицательна на участках убывания функции;
• производная равна 0 в точках экстремума. 

Представим, что мы решили покататься на велосипеде по городу. Участки, на которых мы будем ехать в гору — это участки возрастания функции. Производная в них будет положительна: мы тратим много сил, чтобы подняться по склону вверх.

Остановимся на вершине, чтобы полюбоваться красивой панорамой. Это самая высокая точка горы— точка максимума, которая является экстремумом. 

Теперь спустимся с горы. Будем ли мы прикладывать силы? Нет, велосипед все сделает за нас. То есть производная отрицательна.

Скатившись с горы, мы попадем в самую низкую точку на рельефе, то есть в точку минимума. 

Чуть подробнее про точки минимума и максимума: 

• В точке минимума производная функции меняет знак с минуса на плюс. 
• В точке максимума производная функции меняет знак с плюса на минус. 

Рассмотрим, как эти знания могут пригодиться в решении задач с параметром. 

Как функция отражается в зеркале? Отражением функции в зеркале будет ни что иное, как производная. Именно она с точностью описывает поведение функции, ее характер и внешность.  Поскольку графики функции и производной несколько отличаются друг от друга, то это будет скорее отражение в кривом зеркале, чем в обычном.

Производная функции может пригодиться вам при решении различных заданий из ЕГЭ по профильной математике. Например, частым гостем производная является в номерах 7 и 11. Помимо этого, она может помочь еще и при решении задания второй части №15 на оптимизацию.

Сейчас мы потренируемся решать примеры с помощью производной.

Пример 1. При каких значениях параметра а наименьшее значение функции f(x) = x³ — 48x — a равно -133 на отрезке [-5; -2]?

Решение. 

Шаг 1. Для начала найдем производную функции. 

f'(x) = 3x² — 48 = 3(x² — 16) = 3(x — 4)(x + 4)

Тогда точки экстремума будут равны x = 4 и x = -4. В этих точках производная функции будет менять знак на противоположный.

Шаг 2. Определим, какая из получившихся точек будет точкой максимума, а какая точкой минимума. 

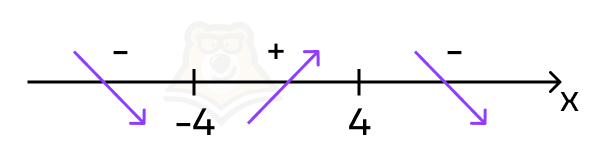
Как не запутаться в точках минимума и максимума при расстановке знаков на прямой? Можно показать стрелочками направление функции: на промежутках с минусом стрелочки смотрят вниз, а на положительных промежутках— вверх. Так мы условно показываем график функции, а значит, можем увидеть точки минимума и максимума визуально.

В точке «4» производная функции меняет знак с минуса на плюс, а значит, это точка минимума. 

В точке «-4» функция меняет знак с плюса на минус — это точка максимума.

Нас интересует значение функции на определенном отрезке, а именно от -2 до -5. Если мы отметим этот участок на прямой, то в него войдет только точка минимума.

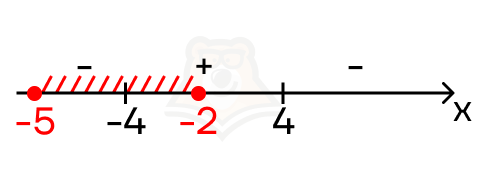
На минутку вспомним нашу поездку на велосипеде. 

Допустим, мы едем по получившейся числовой прямой, включив в точке —2  фитнес-браслет для контроля пульса. От точки —2 до точки 4 будет спуск с горы, а  от точки 4 до 5 будет подъем в гору. 

Браслет был слабо заряжен, и в точке 5 он сел. Мы не успели подняться до вершины горы с включенным браслетом.

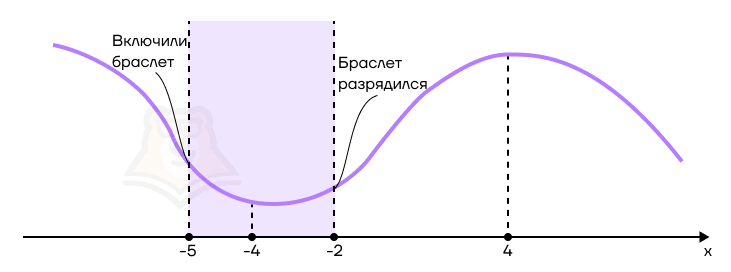
Вопрос: через какую самую низкую точку на маршруте мы проехали, пока работал фитнес-браслет? Через точку минимума, то есть 4. 

Рассмотрим эти же рассуждения на языке математики: до точки -4 функция возрастает, а от -4 до 4 убывает, после точки 4 снова возрастает. Если рассмотреть отрезок от -2 до 5, то от -2 до 4 функция убывает, от 4 до 5 функция возрастает. То есть в точке минимума функция точно будет принимать наименьшее значение. 

Шаг 3. Следовательно, \(f_наим=f(4)=4^3-48*4-a=64-192-a= -128-a\).

Шаг 4. По условию наименьшее значение функции должно быть –133, откуда 

-128-a= -133
a=5

Ответ: 5

Касательная к графику

Касательная к графику — это прямая, которая имеет с графиком только одну общую точку.

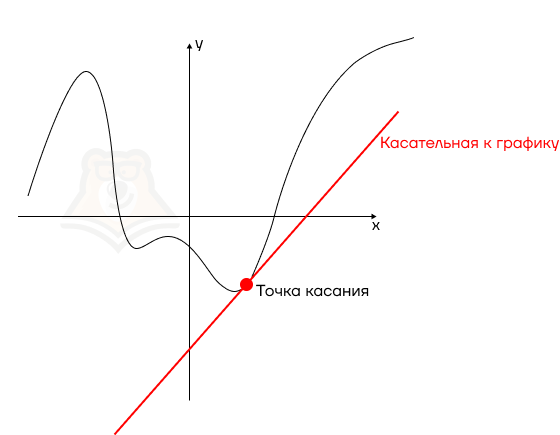
Могут возникнуть вопросы: как задать касательную к графику с помощью уравнения? Как найти координаты точки касания? Как она связана с самой функцией? И на все эти вопросы дает ответ производная функции. 

Геометрический смысл производной: если провести касательную к функции в некоторой точке, то производная функции в этой точке будет равна тангенсу угла ее наклона. 

То есть если мы найдем производную в точке касания, то найдем и угол наклона касательной. 

Рассмотрим некоторую функцию и касательную к ней. Пусть их общая точка будет в х₀, также возьмем произвольную точку в х. 

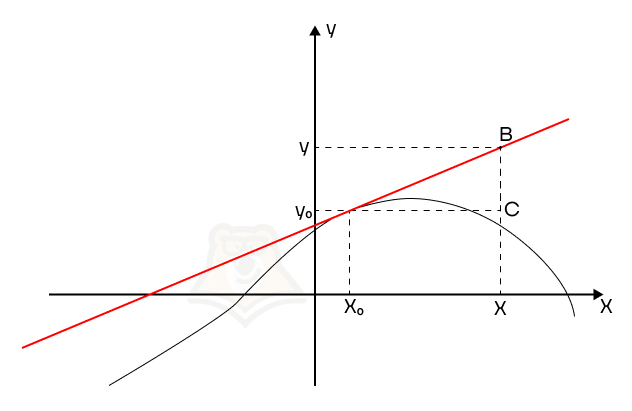
Заметим, что касательная к графику задана уравнением y = kx + b, где k — коэффициент наклона прямой, а следовательно, k = tg(∠BAC)

Найдем тангенс угла наклона:

\(tg(\angle{BAC})=\frac{BC}{AC}=\frac{y — y_0}{x — x_0}\). 

Пусть функция, к которой проведена касательная — это f(x). По геометрическому смыслу производной получаем:

\(f'(x_0) = \frac{y — y_0}{x — x_0}\)

Мы взяли точку х₀, поскольку по геометрическому смыслу производной нам нужна именно точка касания, а не произвольная точка. 

Выразим у:

f'(x₀) * (x — x₀) = y — y₀
y = y₀ + f'(x₀) * (x — x₀)

Немного поменяем обозначения. Поскольку \(y_0\) и \(f(x_0)\) — это одно и то же, то получаем:

y = f(x₀) + f'(x₀) * (x — x₀).

Мы получили уравнение касательной:

y = f(x₀) + f'(x₀) * (x — x₀)

Допустим, нам дана произвольная прямая y = kx + b. Как понять, при каких коэффициентах она будет касательной к графику функции?

Для этого достаточно выполнение одной из двух систем:

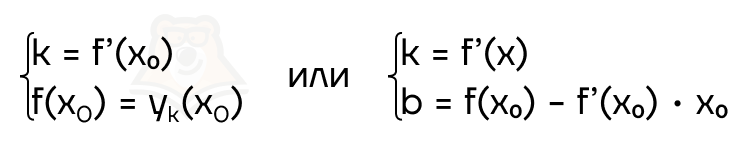
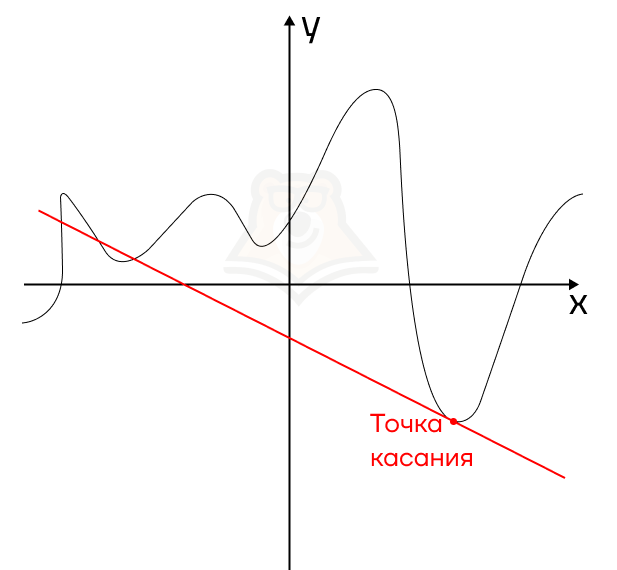
Может ли касательная к функции пересекать ее в другой точке?  Ранее мы встречались с касательной к «Окружности». У них много общего с касательной к графику, но есть одно отличие. Касательная к окружности не может пересечь ее в другой точке, а вот касательная к функции может.  Мы не зря говорим про касательную в точке. Поскольку функция может иметь сложный график, касательная, проведенная к одной точке, может пересечь функцию в другом месте. Пример на изображении ниже.

В ЕГЭ по профильной математике можно встретить касательную функции в задании 7. Поэтому предлагаем вам рассмотреть пример, как применить касательную функции в задачах с параметром, чтобы на экзамене верно и без сомнений решить это задание.

Рассмотрим, где можно применить касательную к функции в задачах с параметром. 

Пример 2. Дана парабола y = x² + ax — 9, касательная к ней проходит через точку (0; -34). При каких значениях параметра а значение функции в точке касания равно 10 при положительных значениях х? 

Решение. 

Шаг 1. Заметим, что дана парабола, ветви которой направлены вверх. 

Шаг 2. Пусть парабола и прямая касаются в точке (x₀; y₀). В уравнении касательной также есть значения х и у. В условии нам дана точка, через которую проходит касательная. Следовательно, y = -34, x = 0. 

Шаг 3. Найдем производную для функции, задающей параболу: y’ = 2x + a, тогда f'(x₀) = 2x₀ + a. 

Шаг 4. Подставим найденные значения в уравнение касательной:
y = f(x₀) + f'(x₀) * (x — x₀)

\(-34 = x_0^2 + ax_0 — 9 + (2x_0 + a)(0 — x_0)\)
\(-34 = x_0^2 + ax_0 — 9 + 2x_0 * 0 — 2x_0^2 + a * 0 — ax_0\)
\(-34 = -x_0^2 — 9\)
\(x_0^2 — 25 = 0\)
(x₀ — 5)(x₀ + 5) = 0
x₀ = 5 и x₀ = -5

Поскольку по условию х₀ должно быть положительно, получаем x₀ = 5. 

Тогда абсцисса точки касания равна 5, откуда можем найти значение функции в точке касания:

y = x² + ax — 9
y = 25 + 5a — 9
y = 16 + 5a

По условию, значение функции в точке касания равно 10, отсюда:

10 = 16 + 5a
5a = -6
a = -1,2

Ответ:  — 1,2

Давайте подведем итог. Что узнали, чему научились?

В этой статье мы разобрали важную тему для экзамена по математике «Производная в задачах с параметром». Знания, которые вы получили после прочтения статьи, пригодятся в нескольких заданиях экзамена. 

Вы научились определять:
— минимум и максимум функции, благодаря чему можете понять, как ведет себя функция; 
— каким уравнением задается касательная, как ее применять в задачах с параметром.

Теперь вам будет проще решать задания 7 и 11 ЕГЭ по профильной математике, а также №15 на оптимизацию.

Термины

Точки экстремума — точка, в которой достигается максимальное или минимальное значение функции на отрезке.

Фактчек

• С помощью производной можно проанализировать функцию, а именно найти промежутки возрастания и убывания, точки экстремума, наибольшее или наименьшее значение функции. 
• Касательная к графику — прямая, которая имеет с графиком только одну общую точку. 
• Касательная задается уравнением y = f(x₀) + f'(x₀) * (x — x₀). 
• Чтобы найти значения коэффициентов в уравнении прямой, при которых она будет касательной к графику, достаточно выполнение одной из двух систем:

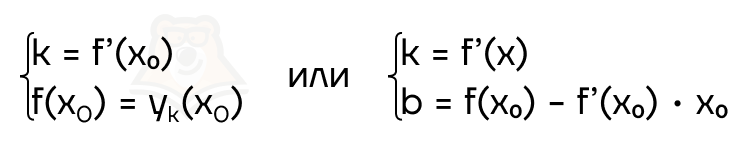
Проверь себя

Задание 1.
В каких точках производная равна 0?

1. В точках экстремума.
2. В точках, где функция возрастает.
3. В точках, где функция убывает.
4. Производная не может быть равна 0.

Задание 2. 
Чему равна производная функции?

1. Тангенсу касательной, проведенной к функции.
2. Котангенсу касательной, проведенной к функции.
3. Синусу касательной, проведенной к функции.
4. Косинусу касательно, проведенной к функции. 

Задание 3.
Как выглядит уравнение касательной?

1. y = f(x₀) — f'(x₀) * (x — x₀)
2. y = f(x) + f'(x₀) * (x — x₀)
3. y = f(x₀) + f'(x₀) * (x — x₀)
4. y = f(x₀) + f'(x₀) *(x₀ — x)

Задание 4.
Чему равен коэффициент наклона k в уравнении прямой y=kx+b?

1. Первообразной функции.
2. Производной функции.
3. Синусу угла наклона касательной.
4. Тангенсу угла наклона произвольной прямой. 

Ответы: 1.— 1 2.— 1 3.— 3 4.— 2