Неравенства и системы неравенств

На этой странице вы узнаете 

• Когда люди «пришли» к понятию неравенств?
• Почему неравенства так важны в жизни?
• Как погода связана с неравенствами?

Как правильно налить в кружку чай или налить тарелку супа? Мы не можем отмерить по линейке количество напитка, но хотим налить примерно полную чашку. Тогда у нас есть верхнее ограничение – верхняя граница кружки, а нижняя граница, на самом деле, у каждого своя, главное, чтобы все были сытыми. В этом просто действие мы сталкиваемся с неравенствами, то есть с выражениями, ответ для которых не конкретное число, а какой-то промежуток значений.

Неравенства – это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. 

В неравенствах левую и правую часть разделяют знаки \(<, >,\leq\) или \(\geq\).

Помимо обычных неравенств, мы можем встретиться с системами неравенств, то есть с выражениями, в которых присутствуют одновременно несколько неравенств. Решение системы – промежуток, значение из которого соответствуют каждому неравенству системы. 

Системы неравенств очень похожи на системы уравнений, только в системах уравнений ответ – число или несколько чисел, а в системе неравенств – промежуток или несколько промежутков чисел. 

Когда люди «пришли» к понятию неравенств? Понятия «больше» и «меньше», как и понятие равенства, возникли при счете предметов и их сравнении друг с другом. Например, понятно, что выгоднее купить больше коров за те же деньги, соответственно надо определить понятие «больше». В книгах понятия неравенства встречаются уже у древних греков, например, Архимед смог указать границы числа π с помощью двойного неравенства.

В этой статье мы узнаем больше про неравенства и системы неравенств, а также научимся их решать.

Линейные неравенства

Мы уже сталкивались с линейными уравнениями, с линейными неравенствами мы должны действовать аналогично. 

Линейные неравенства – неравенства, в которых неизвестное стоит только в первой степени. 

Например, \(5x-1<0\).

В отличие от линейных уравнений, в которых знак равно остается неизменным при решении, в неравенствах есть «ловушка». 

При решении линейных неравенств при делении обеих частей на отрицательное число, мы должны поменять знак неравенства на противоположный. Например, вместо знака получится знак.

Алгоритм решения линейных неравенств.

1 шаг: В правую часть из левой перенести все свободные члены со сменой знака, то есть обычные числа. В левой части должны остаться только слагаемые с x.

2 шаг: Разделить число в правой части на коэффициент при x в левой. Если коэффициент при x меньше нуля, меняем знак неравенства на противоположный. 

3 шаг: В ответ записать получившийся промежуток. Если знак нестрогий ( или ) значение, стоящее в правой части, включаем в ответ с помощью квадратной скобки, если же знак строгий (< или >) значение, стоящее в правой части, не включаем в ответ с помощью круглой скобки.

Разберем, как действовать по этому алгоритму на примере \(-5x+20>0\):

1. Перенесем 20 из левой части в правую, поменяв знак:

\(-5x>-20\)

2. Разделить правую часть на коэффициент при \(x\):

\(x<\frac{-20}{-5}\)
\(x<4\)

Знак поменялся, так как \(-5<0\).

3. Запишем ответ: \((-\infty; 4)\)

В неравенствах ответ записывает с помощью промежутков. Подробнее об этом можно почитать в статье «Метод интервалов».

Почему неравенства так важны в жизни? На самом деле, в жизни мы постоянно сталкиваемся с неравенствами. Например, вы приходите в магазин и хотите понять, какой сырок дороже, тогда надо сравнить две цены друг с другом: определить, какая цена больше, а какая меньше.  Еще один случай, когда мы встречаемся с неравенствами: необходимо заказать, например, мебель, но отдельно надо заплатить за доставку и за сборку, в разных магазинах на все разная цена. Надо определить лучшее предложение, то есть сравнить магазины между собой.

Заметим, что в любых неравенствах мы можем умножать или делить обе части на какое-то ненулевое число и при этом смысл неравенства не изменится.

Например, \(3x+9>12 \leftrightarrow x+3>4\)
Решим оба уравнения: 

• \(3x+9>12\)
  \(3x>3\)
  \(x>1\)

• \(x+3>4\)
  \(x>1\)

Мы разделили обе части исходного неравенства на три, при этом неравенство фактически не изменилось, ответ первого и второго неравенства совпадает.

Линейные неравенства могут встретиться в первой части ОГЭ по математике в задании №13. 

Задание. Укажите решение неравенства \(3(-x+1)-4<2(-x-2)+7\).

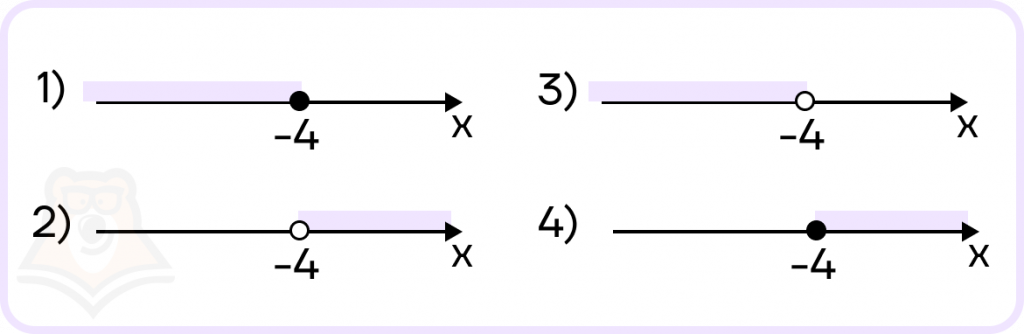
Решение. Решим неравенство, не обращая внимания на варианты ответа: 
\(-3x+3-4<-2x-4+7\)
\(-3x+2x<7-4+4-3\)
\(-x<4\)
\(x>-4\)

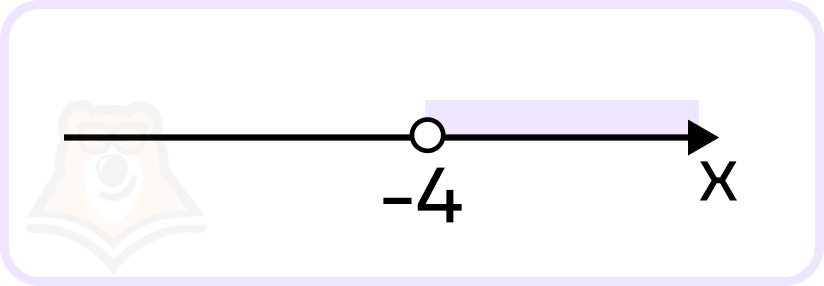
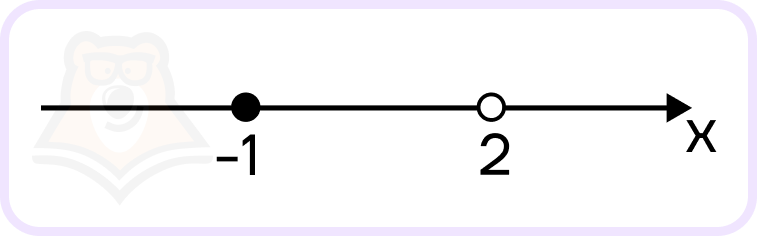
Из данных в условии числовых прямых нам подходит вторая. Она и будет ответом. 

Ответ: 2

Мы научились решать линейные неравенства, рассмотрим квадратные неравенства. 

Квадратные неравенства

Квадратные неравенства выглядят как квадратные уравнения, но со знаком сравнения вместо знака равно. 

Например, \(3x^2+5x-40\).

Как и при решении квадратных уравнений, квадратные неравенства мы решаем с помощью дискриминанта, так как в процессе решения нам необходимо найти корни левой части. 

Разберем, как действовать при решении квадратных неравенств.

Алгоритм решения квадратных неравенств.

1 шаг: Решить левую часть как уравнение, то есть найти корни квадратного выражения, стоящего в левой части. 

2 шаг: Нанести на координатную прямую, получившиеся корни. Если знак строгий (< или >), то числа на координатной оси будут выколотыми (пустыми), если знак нестрогий ( \(\leq\) или \(\geq\)), тогда числа будут закрашенными. 

3 шаг: Посчитать знаки на промежутках с помощью метода интервалов.

4 шаг: В ответ записать те промежутки, знак в которых совпадает со знаком неравенства. Закрашенные значения включаются в ответ с помощью квадратной скобки, пустые – не входят в ответ, скобка круглая. 

Разберем пример: \(x^2+x-2>0\).

1. Найдем корни левой части:

\(x^2+x-2=0\)
\(D=b^2-4ac=1^2-4*(-2)=1+8=9\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-1+\sqrt9}{2}=\frac{-1+3}{2}=\frac{2}{2}=1\)
\(x_2=\frac{-b-\sqrtD}{2a}=\frac{-1-\sqrt9}{2}=\frac{-1-3}{2}=\frac{-4}{2}=-2\)

2. Нанесем корни на координатную прямую:

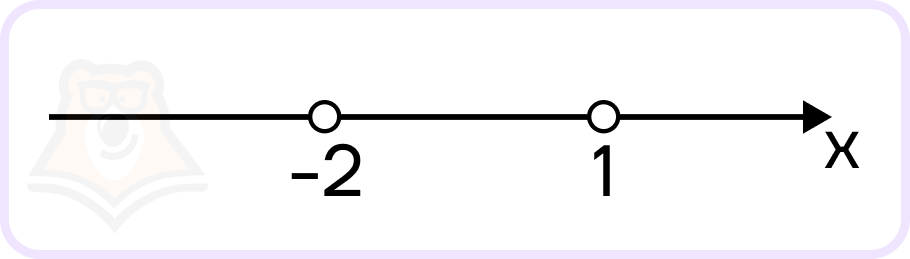
          Точки пустые, так как знак строгий: >.

3. Посчитаем знаки на промежутках:

• Самый правый промежуток (\(1; +\infty \)): возьмем точку, принадлежащую этому промежутку, например, \(x = 2\) и подставим в выражение, стоящее в левой части \(2^2+2-2=4>0\), следовательно, в этом промежутке ставим знак плюс.

• Центральный промежуток (\(-2; 1\)): возьмем точку, принадлежащую этому промежутку, например, \(x = 0\) и подставим в выражение, стоящее в левой части \(0^2+0-2=-2<0\), следовательно, в этом промежутке ставим знак минус.

• Самый левый промежуток (\(-\infty; -2\)): возьмем точку, принадлежащую этому промежутку, например, \(x = -3\) и подставим в выражение, стоящее в левой части \((-3)^2+(-3)-2=9-5=4>0\), следовательно, в этом промежутке ставим знак плюс.

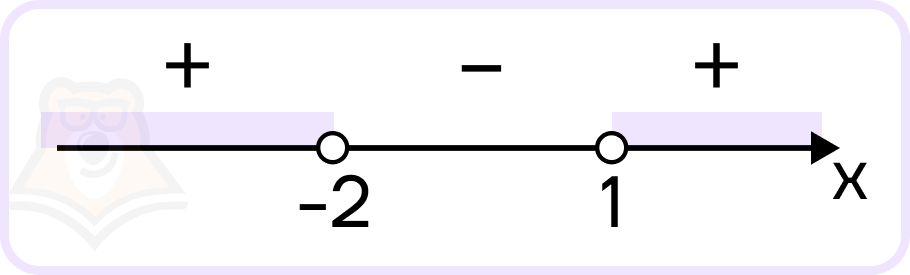
4. В ответ записываем те промежутки, в которых стоит знак, соответствующий знаку неравенства: знак неравенства больше, значит, нам подходят те промежутки, где стоит знак плюс.

Ответ: (-; -2)(1; +).

Квадратные неравенства могут встретиться в ОГЭ в задании № 20.

Задание. Решите неравенство \(4x^2-9x-9>0\).

Решение. Найдем корни левой части:

\(4x^2-9x-9=0\)
\(D=b^2-4ac=(-9)^2-4*4*(-9)=81+16*9=81+144=225\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{9+15}{8}=3\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{9-15}{8}=-\frac{6}{8}=-\frac{3}{4}=-0,75\)

Нанесем корни на координатную прямую:

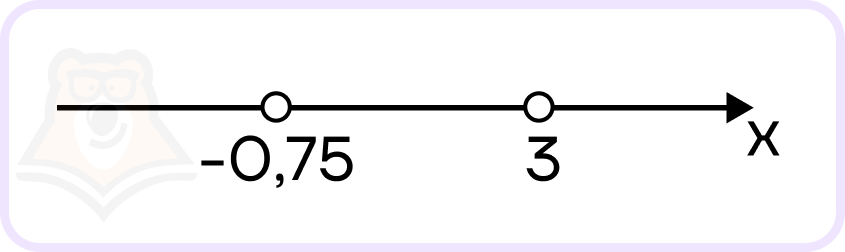
Точки незакрашенные, так как у неравенства знак строгий.

Посчитаем знаки на промежутках:

— (\(3; +\infty \)): возьмем точку \(x=5\), тогда
\(4*5^2-9*5-9=4*25-45-9=100-54=46>0\), в этом промежутке ставим знак плюс.

— (\(-0,75; 3\)): возьмем точку \(x=0\), тогда
\(4*0^2-9*0-9=-9<0\), в этом промежутке ставим знак минус.

— (\(-\infty; -0,75\)): возьмем точку \(x=-5\), тогда
\(4*(-5)^2-9*(-5)-9=4*25+45-9=145-9=146>0\), в этом промежутке ставим знак плюс.

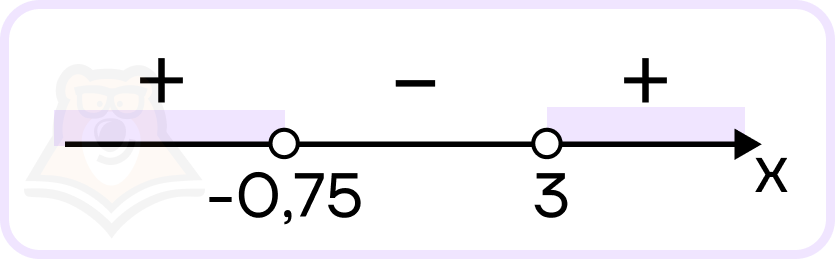
Знак неравенства больше, следовательно, в ответе промежутки со знаками плюс.
Ответ. \((-\infty; -0,75)\cup (3; +\infty )\)

Теперь разберем, как решать тот тип неравенств, который объединяет уже разобранные виды неравенств.   

Дробно-рациональные неравенства

В этом виде неравенств мы сталкиваемся с областью допустимых значений, в выражении, стоящем в левой части, находится дробь, а ее знаменатель не равен нулю, так как мы не можем делить на ноль. 

Дробно-рациональное неравенство – неравенство, в котором есть операции деления на выражение, содержащее переменную.

В числителе и знаменателе левой части могут стоять различные выражения: линейные или квадратные. 

Разберем алгоритм решения таких неравенств.

Алгоритм решения дробно-рациональных неравенств.

1 шаг: Решить как уравнение отдельно числитель и знаменатель левой части. 

2 шаг: Нанести на координатную прямую, получившиеся корни. Если знак строгий (\(<\) или \(>\)), то корни числителя на координатной оси будут выколотыми (пустыми), если знак нестрогий (\(\leq\) или \(\geq\)), тогда числа будут закрашенными. Корни знаменателя всегда выколотые, так мы показываем, что знаменатель всегда не равен нулю.

3 шаг: Посчитать знаки на промежутках с помощью метода интервалов.

4 шаг: В ответ записать те промежутки, знак в которых совпадает со знаком неравенства. Закрашенные значения включаются в ответ с помощью квадратной скобки, пустые – не входят в ответ, скобка круглая. 

Важно отметить, что в неравенствах нельзя сокращать на одинаковую скобку числитель и знаменатель, потому что мы в таком случае потеряем корень, следовательно, получим неправильные промежутки.

Также в ситуации, когда одна и та же скобка стоит и в числителе, и в знаменателе, знаменатель имеет приоритет в расставлении точек. То есть вне зависимости от того, какой знак у неравенства, точку, полученную от этой скобки, мы должны выколоть на числовой прямой. 

Разберем решение таких неравенств на примере \(\frac{(x+2)(x+1)}{(x-3)(x+2)}\leq 0\).

1. Решим уравнения в числителе и знаменателе левой части:

Числитель:
\((x+2)(x+1)=0\)
\(x+2=0\) или \(x+1=0\)
\(x=-2\) или \(x=-1\)

Знаменатель:
\((x-3)(x+2)\neq 0\)
\(x-3\neq 0\) или \(x+2\neq 0\)
\(x\neq 3\) или \(x\neq -2\)

2. Нанесем корни на координатную прямую:

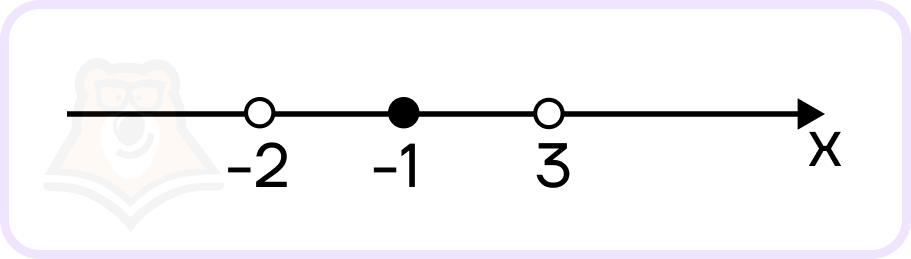
Точки \(-2\) и \(3\) выколоты, так как это корни знаменателя, точка \(1\) – закрашенная, так как это корень числителя и знак неравенства нестрогий. 

3. Посчитаем знаки на промежутках:

• Самый правый промежуток \((3; +\infty)\): возьмем точку, принадлежащую этому промежутку, например, \(x = 4\) и подставим в выражение, стоящее в левой части \(\frac{(4+2)(4+1)}{(4-3)(4+2)}=\frac{6*5}{1*6}=5>0\), следовательно, в этом промежутке ставим знак плюс.

• Второй промежуток \((-1; 3)\): возьмем точку, принадлежащую этому промежутку, например, \(x = 0\) и подставим в выражение, стоящее в левой части \(\frac{(0+2)(0+1)}{(0-3)(0+2)}=\frac{2*1}{-3*2}=-\frac{1}{3}<0\), следовательно, в этом промежутке ставим знак минус.

• Третий промежуток \((-2; -1)\): возьмем точку, принадлежащую этому промежутку, например, \(x = -1,5\) и подставим в выражение, стоящее в левой части \(\frac{(-1,5+2)(-1,5+1)}{(-1,5-3)(-1,5+2)}=\frac{0,5*(-0,5)}{-4,5*0,5}=\frac{0,5}{4,5}=\frac{1}{9}>0\), следовательно, в этом промежутке ставим знак плюс.

• Самый левый промежуток \((-\infty; -2)\): возьмем точку, принадлежащую этому промежутку, например, \(x = -3\) и подставим в выражение, стоящее в левой части \(\frac{(-3+2)(-3+1)}{(-3-3)(-3+2)}=\frac{-1*(-2)}{-6*(-1)}=\frac{2}{6}=\frac{1}{3}>0\), следовательно, в этом промежутке ставим знак плюс.

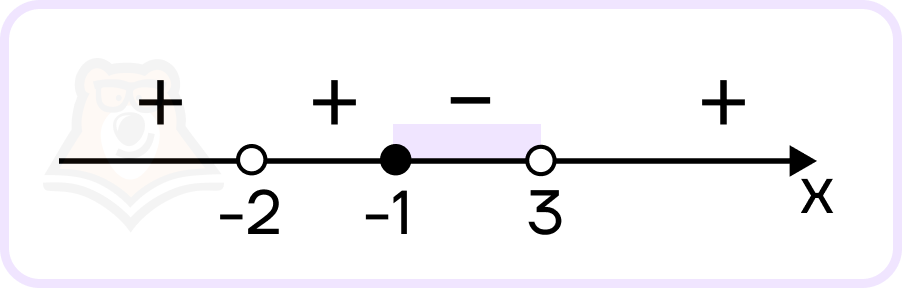
4. В ответ записываем те промежутки, в которых стоит знак, соответствующий знаку неравенства: знак неравенства меньше или равно, значит, нам подходят те промежутки, где стоит знак минус и точки, в которых левая часть обнуляется.

Ответ: [-1; 3).

Данный тип неравенств может встретиться в задании №20 в ОГЭ по математике.

Задание. Решите неравенство \(\frac{x+1}{x-2}\leq 0\).

Решение. Найдем корни числителя и знаменателя: 
\(x+1=0; x-2\neq 0\)
\(x=-1\)
\(x\neq 2\)

Нанесем точки на числовую ось:

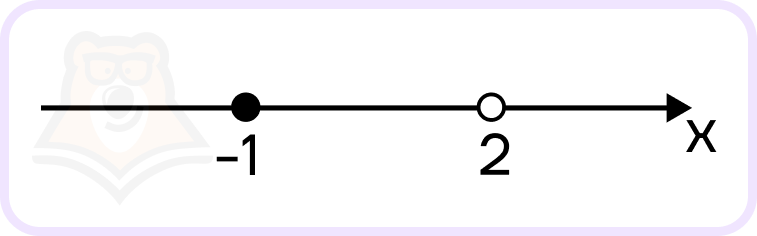
\(x=-1\) — закрашенная точка, так как знак неравенства нестрогий, \(x=2\) — пустая точка, так как знаменатель не равен нулю.

Посчитаем знаки на промежутках:

— (\(2; +\infty \)): возьмем точку \(x=3\), тогда \(\frac{3+1}{3-2}=4>0\), в этом промежутке ставим знак плюс.

— (\(-1; 2\)): возьмем точку \(x=0\), тогда \(\frac{0+1}{0-2}=-\frac{1}{2}<0\), в этом промежутке ставим знак минус.

— (\(-\infty; -1\)): возьмем точку \(x=-2\), тогда \(\frac{-2+1}{-2-2}=\frac{1}{4}>0\), в этом промежутке ставим знак плюс.

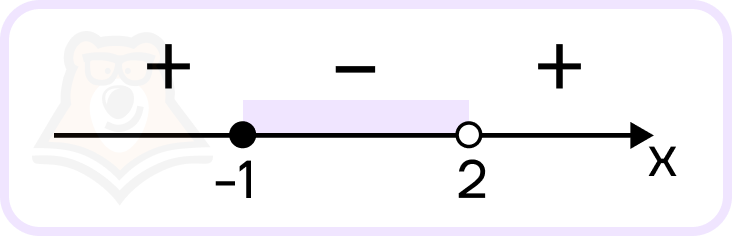
Знак неравенства «меньше», следовательно, нам подходит промежуток со знаком минус.
Ответ. \([-1; 2)\)

Далее рассмотрим, как решать системы неравенств.

Системы неравенств

В некоторых ситуациях нам может не хватить только одного неравенства: например, мы хотим приготовить торт или пирожки, но пока мы не знаем точно, что будем готовить.

Тогда, придя в магазин, нам нужно купить такое примерное количество муки, чтобы хватило и на торт, и на пирог. Эту ситуацию можно описать системой неравенств, в котором первое неравенство определяет нам количество муки, необходимой на торт, а второе – на пирожки. 

Решением такого неравенства будет количество муки, подходящее одновременно под два случая. 

Система неравенств – несколько неравенств,  для которых требуется найти множество всех решений, являющихся одновременно решениями каждого неравенства системы.

Если у двух неравенств в системе нет чисел, которые являются решениями и первого, и второго неравенства, то мы говорим, что у системы неравенств нет решения, хотя у каждого неравенства по отдельности решение есть.

Но если все-таки решение есть, как найти этот промежуток? 

Алгоритм решения систем неравенств

1 шаг: Решить отдельно каждое неравенство системы.

2 шаг: На координатной прямой обозначить промежутки – решение каждого неравенства. 

3 шаг: Найти пересечение закрашенный областей всех координатных прямых, это пересечение и есть решение системы.

Разберем алгоритм на примере: 

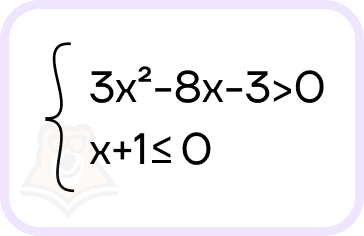
1. Решим сначала первое неравенство: \(3x^2-8x-3>0\)

Найдем корни левой части:

\(3×2-8x-3=0\)
\(D=b2-4ac=(-8)2-4*3*(-3)=64+36=100\)
\(x1=-b+D2a=8+1006=186=3\)
\(x2=-b-D2a=8-1006=-26-13\)

Нанесем корни на координатную прямую:

Точки выколоты, так как у неравенства знак строгий.

Посчитаем знаки на промежутках:

• \((3; +\infty)\): возьмем точку \(x=4\), тогда \(3*4^2-8*4-3=48-32-3=48 -35 = 13>0\), в этом промежутке ставим знак плюс.

• \((-\frac{1}{3}; 3)\): возьмем точку \(x=0\), тогда \(3*0^2-8*0-3=-3<0\), в этом промежутке ставим знак минус.

• \((-\infty; -\frac{1}{3})\): возьмем точку \(x=-1\), тогда \(3*(-1)^2-8*(-1)-3=3+8-3=8>0\), в этом промежутке ставим знак плюс.

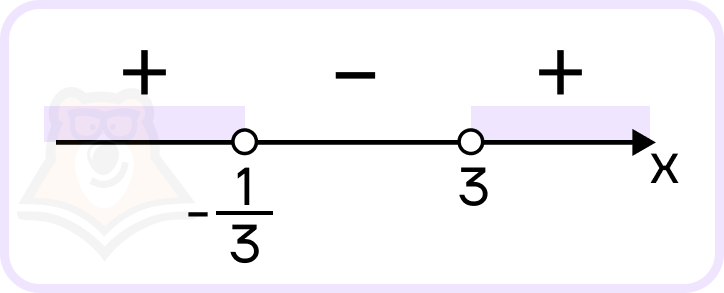
Знак неравенства «больше», следовательно, нам подходят промежутки со знаком плюс.

2. Решим второе неравенство: \(x+1\leq 0\)

\(x\leq -1\)

3. Найдем пересечение решений двух неравенств системы:

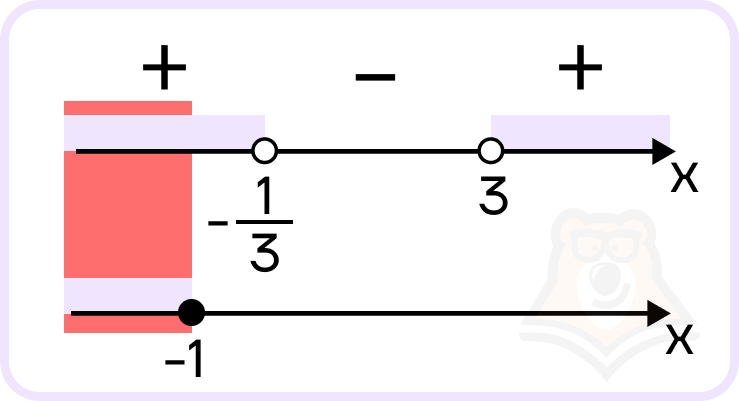
На самом деле, можно не рисовать две отдельные прямые для двух разных неравенств, другой вариант чертежа: нарисовать одну прямую и разной штриховкой или с двух разных сторон обозначить решение каждого неравенства. 

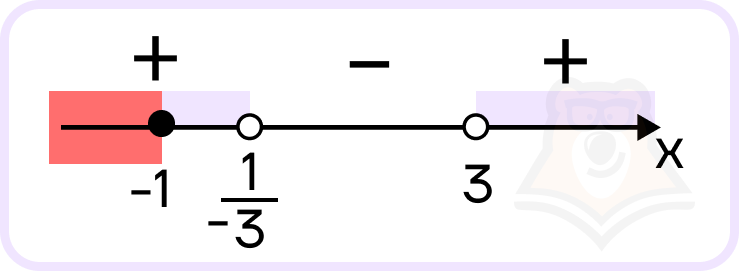
4. В ответ запишем промежуток пересечения решений двух неравенств.

Ответ: \((-\infty; 1]\)

Как погода связана с неравенствами? В прогнозе погоды нам говорят только наименьшую и наибольшую температуру: мы узнаем промежуток, в котором будет находиться температура в течении суток. То есть мы имеем двойное неравенство, описывающее погоду. Также иногда нам может прийти сообщение о том, что ветер в определенном регионе может достигать какого-то количества метров в секунду. И это опять неравенство, мы понимаем, что ветер будет либо меньше, либо равен указанной отметки.

В системе могут стоять любые неравенства: и линейные, и квадратные, и дробно-рациональные, и иррациональные. О последних поговорим далее. 

Иррациональные неравенства

Иррациональные неравенства – неравенства, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень.

Так как неизвестная находится под корнем, мы сталкиваемся с ОДЗ корня, таким образом, мы должны решить не только неравенство, но и учесть, что подкоренное выражение не должно быть меньше нуля. Вот тут и появляется система.

Алгоритм решения иррациональных неравенств

1 шаг: Составить систему неравенств, где первое неравенство – область допустимых значений подкоренного выражения ( подкоренное выражение не отрицательное), а второе неравенство – исходное выражение. 

2 шаг: Решить каждое неравенство отдельно. В случае решения иррационального неравенства мы должны обе части возвести в квадрат и затем решить получившееся линейное или квадратное неравенство. 

3 шаг: Найти пересечения решений первого и второго неравенства. Записать этот промежуток пересечения в ответ. 

Разберем пример: \(\sqrt{x+3}>2\)

1. Запишем систему неравенств:

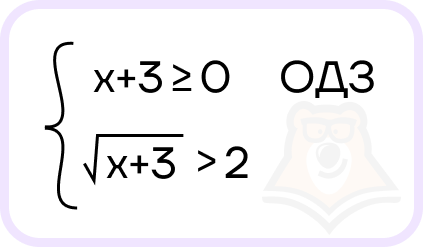
2. Решим каждое уравнение системы:

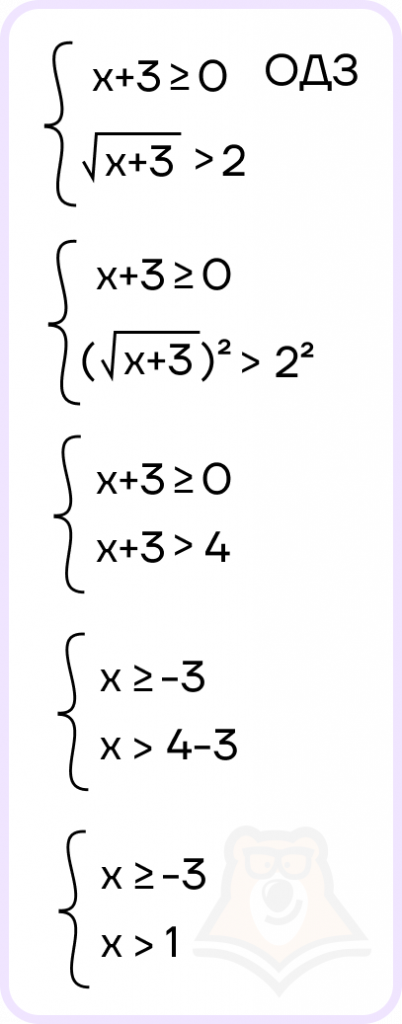
3. Нанесем решения каждого уравнения на две разные координатные прямые и найдем пересечения этих решений:

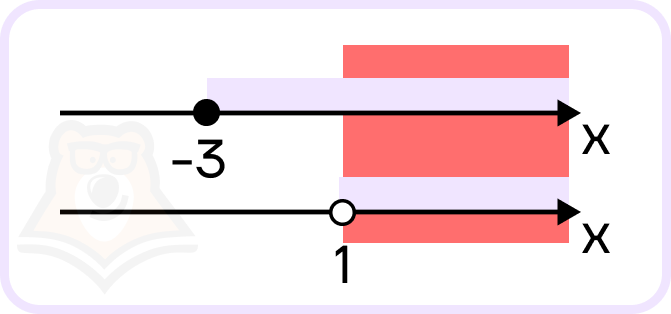
4. Запишем промежуток пересечения в ответ:

Ответ: \((1; +\infty)\)

Данный вид неравенств может встретить в задании №20 ОГЭ по профильной математике.

Задание. Решите неравенство \(\sqrt{2x+1}\leq 1\).

Решение. Составим систему:

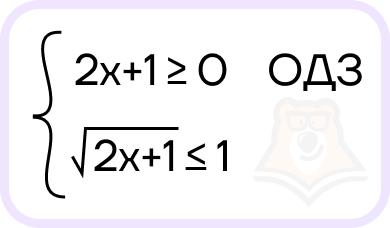
Решим каждое уравнение системы:

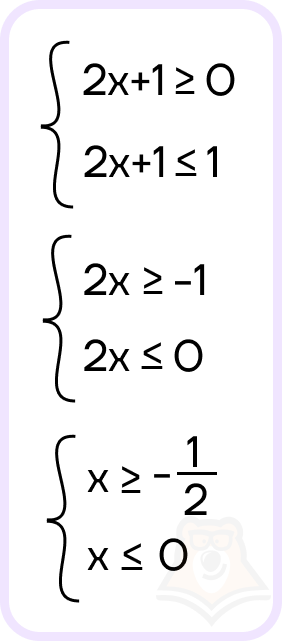
Нанесем решения на числовые прямые и найдем пересечение:

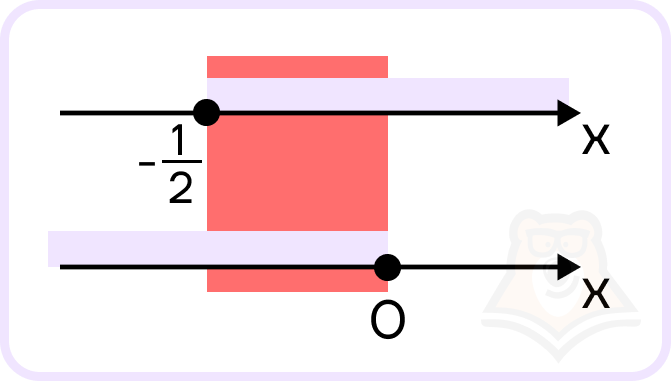
Запишем промежуток, полученный на пересечении в ответ.
Ответ. \([-12; 0]\)

Сегодня мы узнали, какие виды неравенств бывают и как решать каждый из них. А также разобрались с системами неравенств. Чтобы продолжить изучение математики, переходите к нашей следующей статье «Точка, прямая, луч, отрезок и угол».

Термины

Координатная прямая (числовая ось) – это прямая с указанным на ней началом отсчета, направлением отсчета, единичным отрезком.  

Фактчек

• Неравенство – выражения, где между левой и правой частью стоят знаки \(<, >,\leq\) или \(\geq\).
• Неравенства бывают линейными, квадратными, дробно-рациональными или иррациональными. В случае с дробно-рациональными и иррациональными мы должны учесть ОДЗ в выражениях с переменной. 
• Система неравенств – несколько неравенств, для которых требуется найти множество всех решений, являющихся одновременно решениями каждого неравенства системы.
• Решение системы неравенств – промежуток, удовлетворяющий всем неравенствам системы одновременно.

Проверь себя

Задание 1.
Какое выражение является неравенством?

1. \(3x^2+2y^2=0\)
2. \(3cos^2x=0\)
3. \(2x+3x^3>0\)
4. \(10x^3-4x^2y+6xy^2=0\)

Задание 2.
Что является решение квадратного неравенства \(2x^2+3x-2<0\)?

1. \((-2, -\frac{1}{2})\)
2. \((-2, -\frac{1}{2}]\)
3. \((-\infty, -2); (-\frac{1}{2};+\infty)\)
4. \([-2, -\frac{1}{2}]\)

Задание 3.
Что является решением дробно-рационального неравенства \(\frac{x+1}{2x^2-x+1}\leq0\)?

1. \((-\infty; -1]\)
2. \([-1;+\infty)\)
3. \((-1;+\infty)\)
4. \((-\infty; -1)\)

Задание 4.
Что является решением иррационального неравенства \(\sqrt{x+2}>x\)?

1. \([-2; 2]\)
2. \((-2; 2]\)
3. \((-2; 2)\)
4. \([-2; 2)\)

Задание 5.
Что является решением системы неравенств ?

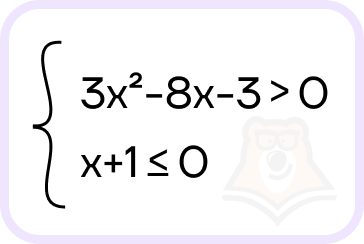
1. \((-\infty; -1]\)
2. \((-\infty; -1)\)
3. \([-1; +\infty)\)
4. \([-1; 1)\)

Ответы: 1. — 3 2. — 1 3. — 2 4. — 4 5.— 1