Дробно-рациональная функция

На этой странице вы узнаете 

• Как связана медицина и дробно-рациональная функция?
• Почему в дробно-рациональных неравенствах нельзя сокращать на одинаковую скобку?
• Как правильно находить ОДЗ на экзаменах?

Как успеть все запланированные дела? Техники тайм-менеджмента предлагают отбрасывать на самом деле ненужные дела, а в случае, если какое-то дело все-таки нужно выполнить, его необходимо разбить на более маленькие задачи.

На самом деле что-то подобное мы должны делать с дробно-рациональными функциями.

Дробно-рациональная функция – это функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются многочлены.

Если в числителе и знаменателе есть общая скобка, мы можем сократить на нее, предварительно вычислив область допустимых значений (ОДЗ). Если же одинаковой скобки нет, мы должны разделить числитель на знаменатель и, таким образом, разбить дробное выражение на сумму двух слагаемых.

В этой статье мы разберем подробнее, как действовать в каждом из этих случаев.

Как связана медицина и дробно-рациональная функция? В медицине активно используются дробно-рациональные функции для моделирования биологических процессов. Например, при описании динамики распространения заболеваний и при прогнозировании эффективности новых лекарств.

Работа с дробно-рациональными функциями

Рассмотрим, в каком случае мы понимаем, что данная нам функция дробно-рациональная. Как уже было сказано раньше, во-первых, функция должна представлять собой дробное выражение, во-вторых, в числителе и знаменателе этой дроби должны стоять многочлены. 

То есть функция \(y =\frac{ Q(x)}{P(x)}\), где \(Q(x)\) и \(P(x)\) – полиномы разных степеней. Например, \(y =\frac{ x+2}{x^2+2x+3}\) или \(y=\frac{x^3+2x}{x+1}\).

При взгляде на любую функцию сразу возникает желание построить функцию по точкам, то есть перебрать различные x и, соответственно, y. Но на самом деле это возможно только в элементарных функциях, в данном случае мы получим просто набор точек, закономерность расположения которых не сможем понять.

Значит, нам нужно найти другой способ построения данных функций.

При построении графика такой функции первым делом необходимо найти область допустимых значений аргумента этой функции.

Мы знаем, что на ноль делить нельзя. Значит, сначала мы должны обозначить, что знаменатель нашей функции не равен нулю. 

Почему в дробно-рациональных неравенствах нельзя сокращать на одинаковую скобку? В уравнениях и функциях после нахождения ОДЗ можно сократить одинаковую скобку в числителе и знаменателе без потери корней. Но если то же самое сделать с неравенством, мы потеряем один или несколько промежутков, которые будут являться решениями, поэтому это недопустимо.

Если в числителе и знаменателе есть общая скобка, мы можем сократить на нее, предварительно вычислив область допустимых значений (ОДЗ). Если же одинаковой скобки нет, мы должны разделить числитель на знаменатель и, таким образом, разбить дробное выражение на сумму двух слагаемых.

Рассмотрим пример: \(y =\frac{x^2+6x+8}{x+2}\)

Найдем ОДЗ этого выражения: 

\(x+2 ≠ 0\)
\(x ≠ -2\)

После нахождения ОДЗ мы должны проверить, нет ли в числителе и знаменателе одинаковой скобки.

Мы уже знаем, что в числителе и знаменателе дроби могут стоять не только линейные, но и выражения более высоких степеней. Следовательно, для выделения общей скобки мы должны преобразовать выражения, находящиеся в числителе и знаменателе дроби, то есть разложить на множители числитель и знаменатель. Для совершения преобразований мы можем: 

• использовать формулы сокращенного умножения; 
• выносить общие множители; 
• разложить на множители квадратное выражение;
• использовать метод группировки.

Затем после разложения на множители, нам нужно сократить одинаковую скобку в числителе и знаменателе дроби. Таким образом, мы упростили функцию и можем уже построить получившуюся функцию с учетом ОДЗ.

Разложим квадратное уравнение на множители по формуле: \(ax^2+bx+c=a(x-x_1)(x-x_2)\), где \(x_1, x_2\) — корни квадратного уравнения.

Найдем корни числителя 

\(x^2+6x+8=0\)
\(D=b^2-4ac=36-4*8=36-32=4\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-6+2}{2}=-2\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-6-2}{2}=-4\)

Тогда \(x^2+6x+8=(x+2)(x+4)\)

Перепишем дробь: 

\(y = \frac{x^2+6x+8}{x+2}=\frac{(x+2)(x+4)}{x+2}=x+4\)

Теперь мы можем построить график функции \(y=x+4\). При этом мы должны на графике выколоть точку \(-2\), так как мы нашли, что \(x ≠ -2\).

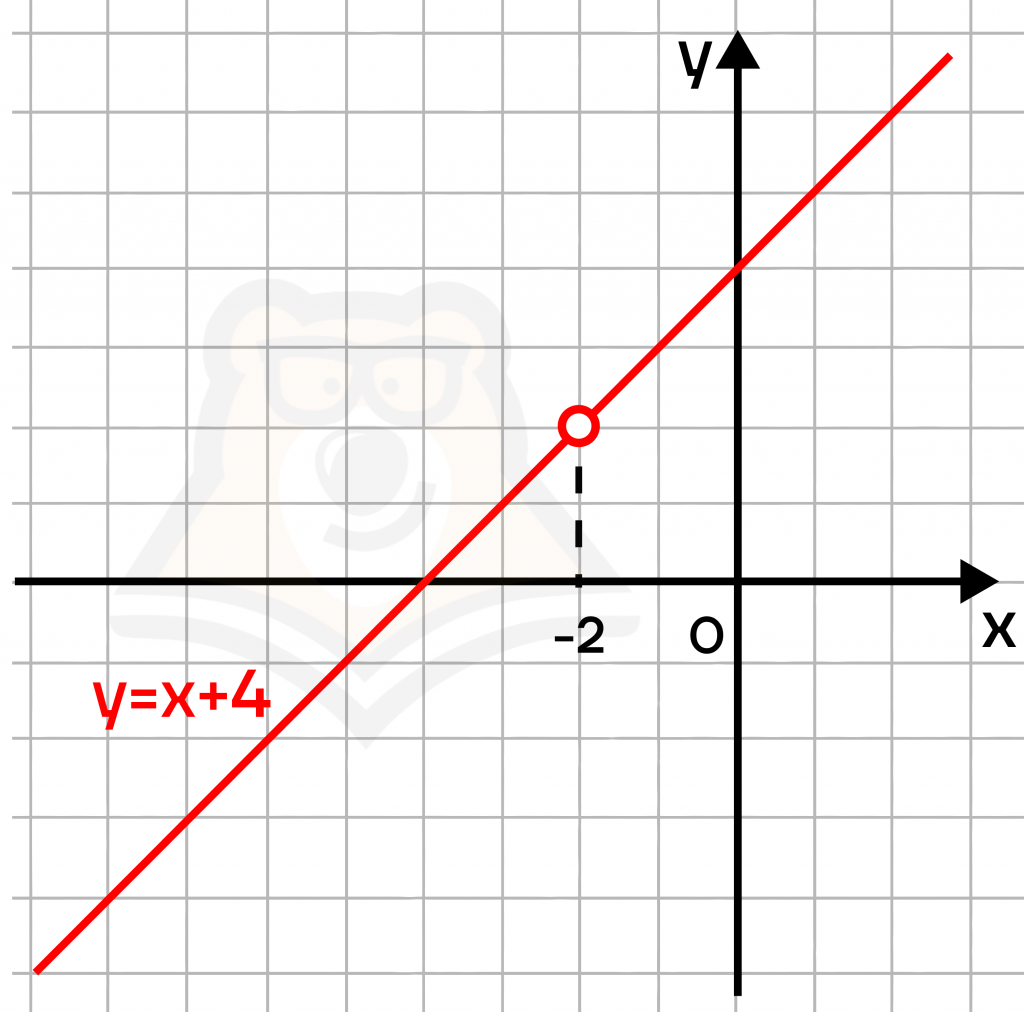
В ОГЭ по математике в задании №22 нам может встретиться дробно-рациональная функция, которую после преобразований мы можем превратить в одну из элементарных функции.

Задание. Постройте график функции \(y=\frac{x-5}{x^2-8x+15}\) и определите, при каких m прямая y=m не имеет точек пересечения с графиком.

Решение. Найдем ОДЗ:

\(x^2-8x+15 ≠ 0\)
\(D = 64-4*15=4\)
\(x_1 ≠ \frac{8+2}{2} ≠ 5\)
\(x_2 ≠ \frac{8-2}{2} ≠ 3\)

Разложим знаменатель на множители и перепишем дробь: 

\(y =\frac{ x-5}{(x-5)(x-3)}\)

Сократим на одинаковую скобку:

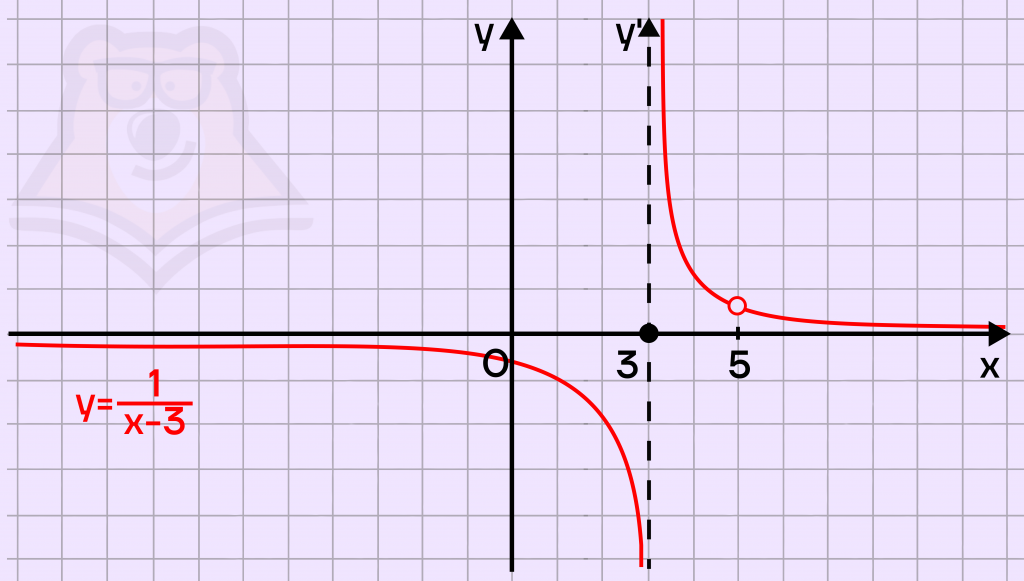
\(y =\frac{1}{x-3}\)

Данное уравнение – уравнение гиперболы, с центром в точке (\(3; 0\))

Построим данную функцию с учетом ОДЗ:

Будем как бы вести линейкой сверху вниз, находя те положения, в которых нет пересечений.

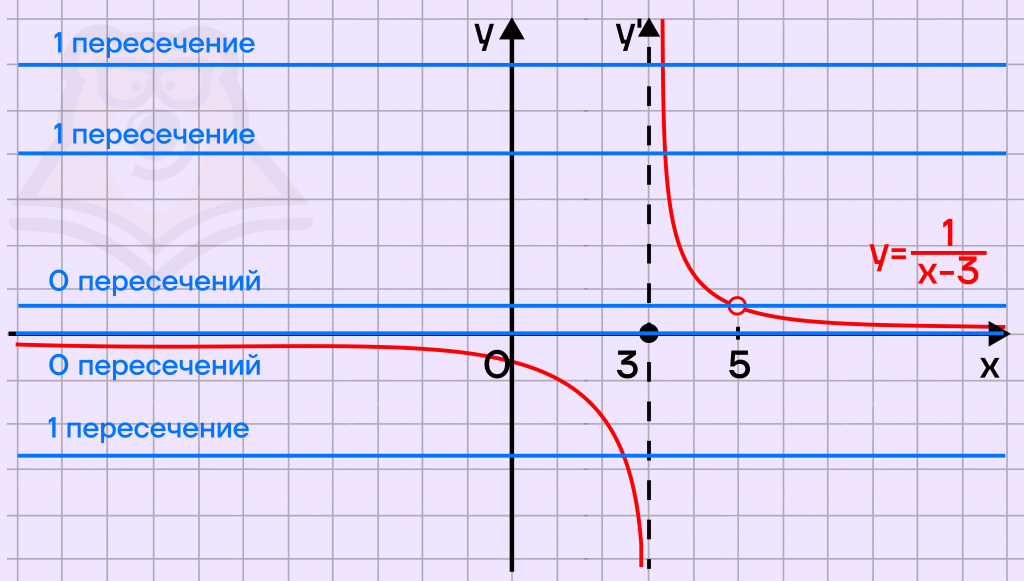
Пересечений нет, если \(y=0\), а также если прямая проходит через точку \(x=5\). При \(x=5\) можем найти \(y\), подставив \(y\) в уравнение гиперболы: \(y=\frac{1}{5-3}=\frac{1}{2}=0,5\).
Ответ. 0, 0,5

Итак, мы получили алгоритм, по которому мы работаем с дробно-рациональной функцией, если в числителе и знаменателе есть общая скобка:

Алгоритм работы с дробно-рациональной функцией

1 шаг: Найти ОДЗ функции: знаменатель дроби не равен нулю.

2 шаг: Разложить числитель и знаменатель на множители.

3 шаг: Сократить одинаковые скобки в числителе и знаменателе.

4 шаг: Построить получившуюся элементарную функцию.

5 шаг: Учесть ОДЗ, выколоть на графики точки, которые не входят в область допустимых значений.

Но что делать, если в числителе и знаменателе нет общей скобки? В таком случае мы не можем сделать функцию более «простой», значит, нужно действовать по-другому. 

Деление многочлена на многочлен

После того как мы нашли ОДЗ и увидели, что общей скобки в числителе и знаменателе нет, нам необходимо выделить целую часть, то есть представить график в виде \(y = n+\frac{k}{Q(x)}\), где \(n, k\) — какие-то числа, \(Q(x)\) — многочлен какой-то степени.

Каким же способом можно выделить целую часть дробно-рациональной функции?

Разберем два способа:

1 способ

1 шаг: Мы должны таким образом преобразовать числитель, чтобы выделить там скобку, которая была бы равна знаменателю дроби. Таким образом, мы должны представить дробь в виде \(y=\frac{kY+X}{Y}\), где \(k\)- какое-то число, \(Y\) — выражение из знаменателя, \(X\) — оставшиеся слагаемые числителя. 

2 шаг: Преобразуем функцию \(y=\frac{kY+X}{Y}=\frac{kY}{Y}+\frac{X}{Y}=k+\frac{X}{Y}\).

3 шаг: Построить получившуюся функцию.

Разберемся на примере: \(y=\frac{2x-6}{x-1}\)

Преобразуем выражение, стоящее в правой части:

\(y=\frac{2x-6}{x-1}=\frac{2x-2-4}{x-1}=\frac{2(x-1)-4}{x-1}=\frac{2(x-1)}{x-1}-\frac{4}{x-1}=2-\frac{4}{x-1}\).

Построим получившуюся функцию: это гипербола, центр которой перенесем в точку (\(1; 2\)). В новой системе координат строим функцию \(y=-\frac{4}{x}\).

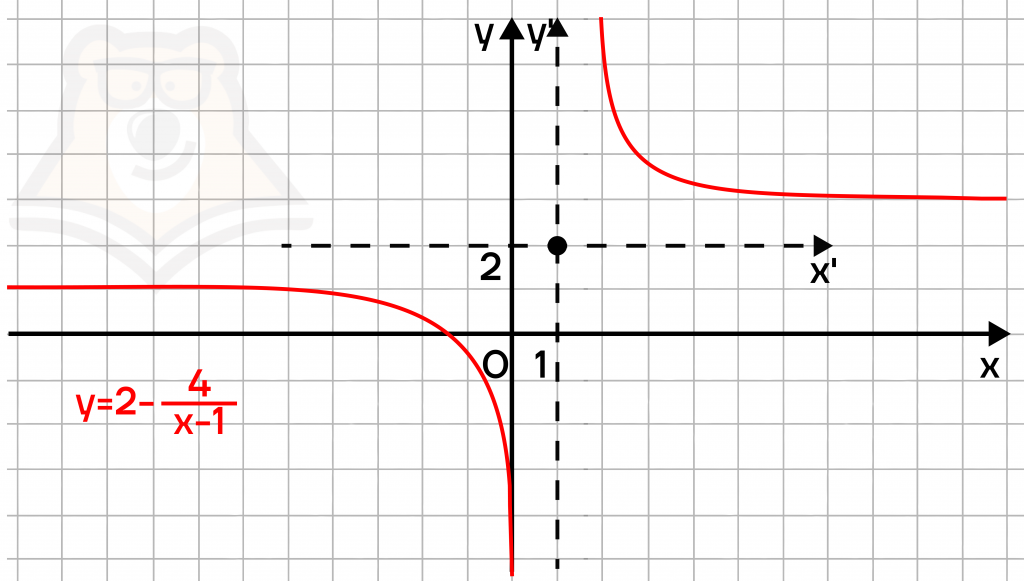
Разберем другой способ выделения целой части.

2 способ

1 шаг: Разделить в столбик числитель на знаменатель. При делении мы должны так подбирать частное, чтобы при каждом шаге уничтожать большую степень. 

На самом деле, деление многочлена на многочлен очень похоже на деление целых чисел, мы также подбираем частное, чтобы уничтожать большие разряды, а затем остаток от деления сносим.

2 шаг: Мы должны преобразовать функцию к виду \(y = n+\frac{k}{Q(x)}\), здесь \(n\) – частное, \(k\) – остаток от деления, \(Q(x)\) – знаменатель исходной дроби.

3 шаг: Построить получившуюся функцию.

В данном случае мы действуем по теореме Безу, о которой мы подробно говорили в статье «Преобразование алгебраических выражений. Часть 2». Отличие только в том, что при решении уравнения с помощью теоремы Безу мы ожидаем, что остаток при делении будет равен нулю, а в данном случае остаток чаще всего ненулевой.

Например, \(y=\frac{3x-2}{x-3}\)

Разделим числитель на знаменатель:

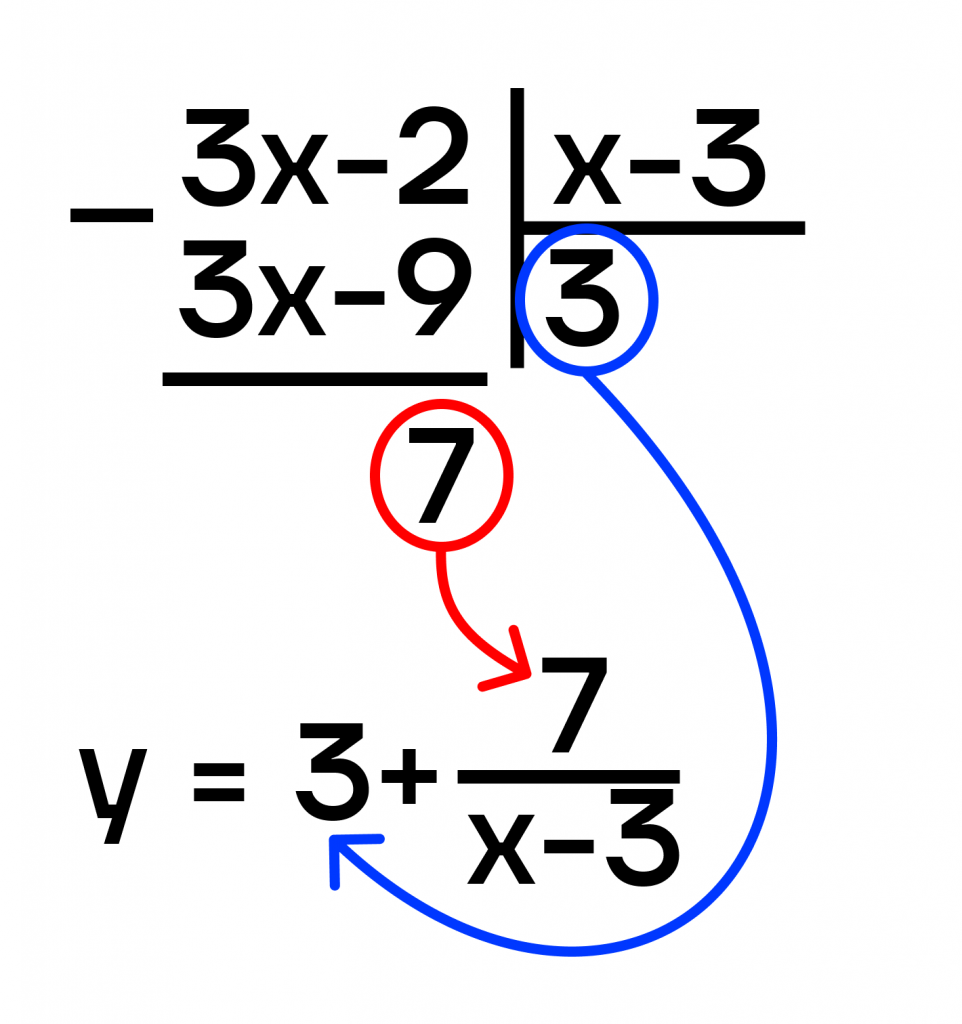
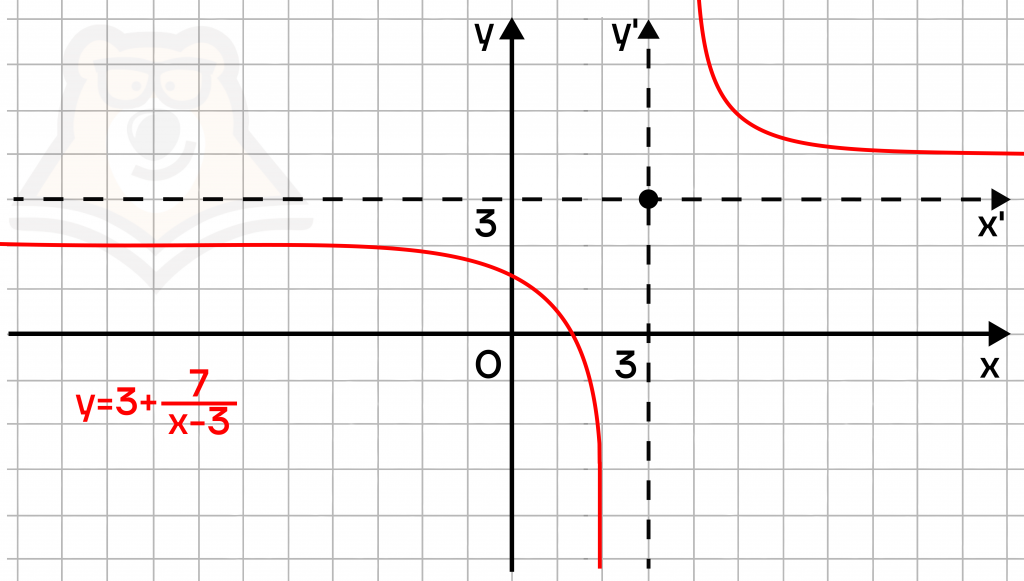
Построим график функции \(y=\frac{3x-2}{x-3}=3+\frac{7}{x-3}\).

Как правильно находить ОДЗ на экзаменах? Недавно поднялся вопрос о том, можно ли писать ОДЗ при решении уравнения или неравенства на ОГЭ и ЕГЭ. Эксперты ФИПИ дали ответ, что писать ОДЗ можно.  Но важно написать все ограничения, которые присутствуют в данном выражении. То есть если у нас в выражении есть и знаменатель, и, например, логарифм мы должны написать ограничения для каждого из этих элементов и взять их в систему. Тогда это будет правильно и вам зачтут такое решение.

Но как проверить, что мы все сделали правильно и действительно верно выделили целую часть? 

Мы должны сложить или вычесть получившееся целое число и дробь, подведя их под общий знаменатель и затем преобразовать числитель. Если после этих действий мы получили исходную дробь, значит, мы правильно выделили целую часть.

Например, представим, что мы уже выделили целую часть и получили функцию \(y =3- \frac{4}{x-5}\), найдем исходную функцию?

\(y=\frac{3(x-5)-4}{x-5}\) | подвели два слагаемых под общий знаменатель
\(y=\frac{3x-15-4}{x-5}=\frac{3x-19}{x-5}\)

Дробно-рациональная функция, в которой мы должны выделить целую часть, может встретиться в ОГЭ по математике в задании №22.

Задание. Постройте график функции
\(y=\frac{x^2-3x-4}{x+1}\) и определите, при каких m прямая \(y=m\) имеет одну точку пересечения.

Решение. Найдем ОДЗ:

\(x+1 ≠ 0\)
\(x ≠ -1\)

Разделим числитель на знаменатель:

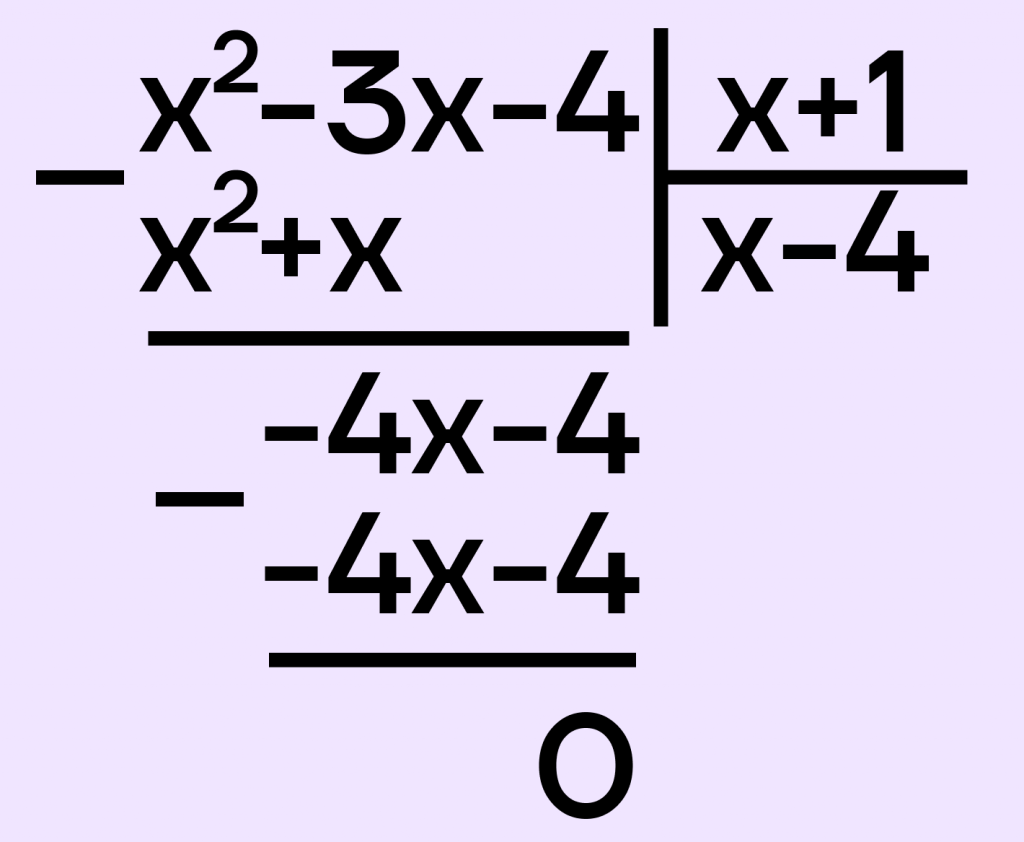
\(y = 0+x-4=x-4\)

Построим график этой функции с учетом ОДЗ:

x	0	1
y	-4	-3

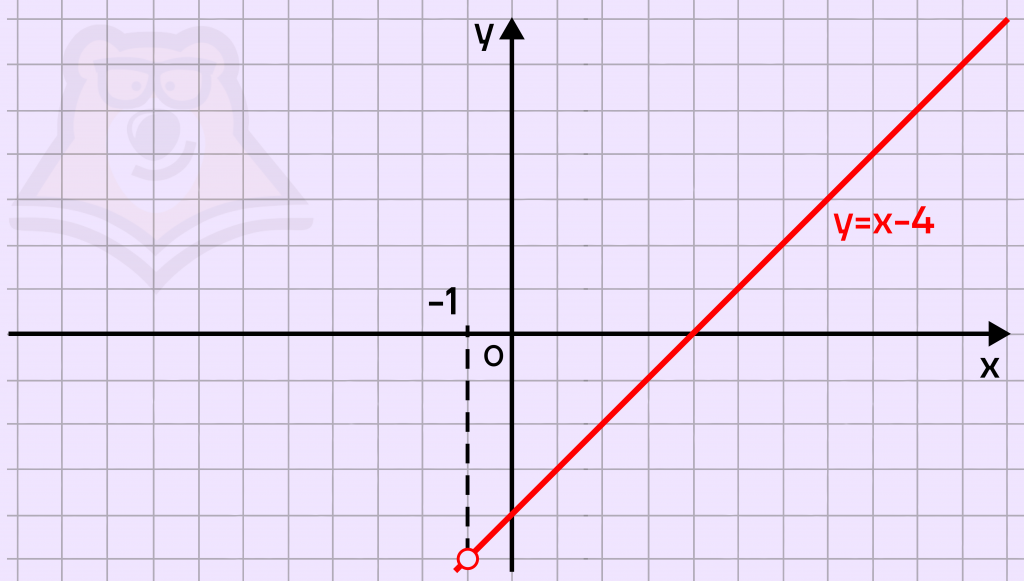
Найдем те m, при которых прямая \(y=m\) имеет одну точку пересечения с графиком \(y=m\).

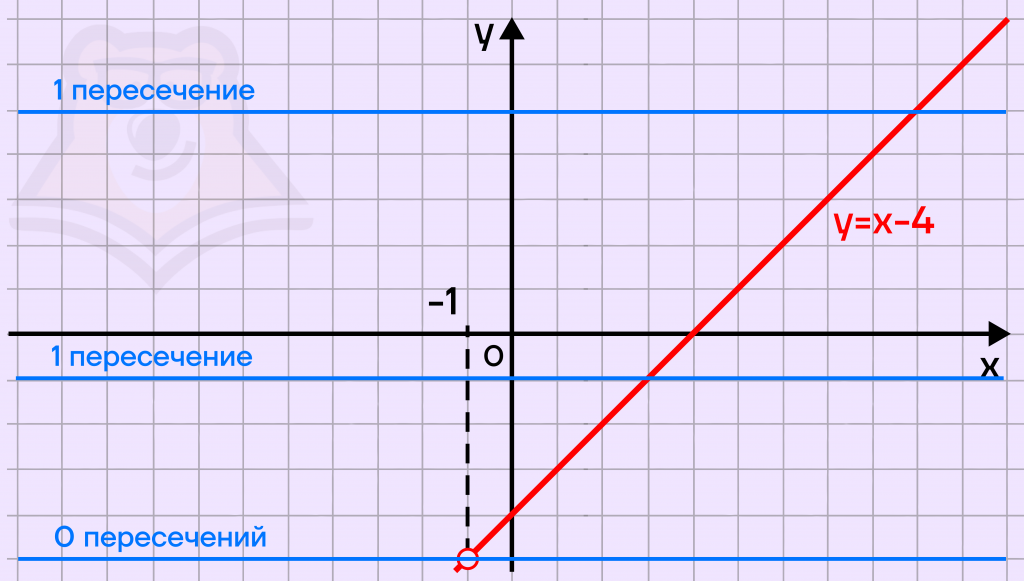
Прямая не имеет точек пересечения в точке \(x=-1\), найдем y в этой точке: \(y = -1-4=-5\). В остальных точках мы имеем одну точку пересечения.

Ответ. (\(-\infty; -5)(-5; +\infty\))

Дробно-рациональные функции используются в различных практических науках: физике, экономике, инженерии. В этой статье мы разобрались, как строить дробно-рациональные функции и где их можно встретить на экзаменах. Продолжайте дальше изучать математику вместе с нами, читайте нашу следующую статью «Финансовые задачи».

Термины

Многочлен (полином) – выражение, состоящее из неопределенных (также называемых переменными) и коэффициентов, которое включает в себя только операции сложения, вычитания, умножения и неотрицательного целочисленного возведения переменных в степень. 

Область допустимых значений (ОДЗ) – множество всех значений переменной, при которых выражение определено.

Разряды чисел – это место (позиция) цифры в записи данного числа. 

Фактчек

• Дробно-рациональная функция – функция вида \(y =\frac{f(x)}{g(x)}\), где \(f(x)\) и \(g(x)\) — некоторые функции.
• Для построения дробно-рациональной функции мы должны либо выделить целую часть, либо сократить общую скобку числителя и знаменателя.
• При выделении целой части мы можем действовать двумя способами. Первый вариант: преобразовать числитель и разбить дробь на два слагаемых, в одном из которых в числителе и знаменателе должна быть одинаковая скобка, сократив которую мы получим целое число. Второй – разделить числитель на знаменатель.

Проверь себя

Задание 1.
Чему равна область допустимых значений функции \(y =\frac{x^2-3x+2}{(x+3)(x-1)}\)?

1. \(x ≠ 1\)
2. \(x ≠ 1, -3\)
3. \(x ≠ 2, 1, -3\)
4. \(x ≠ 2, 1\)

Задание 2.
Чему равна общая скобка числителя и знаменателя функции \(y =\frac{x^2-x}{(x-1)(x-2)}\)?

1. \(x-2\)
2. \(x\)
3. \(x-1\)
4. \(x^2-x\)

Задание 3.
Чему равна функция \(y =\frac{3x-5}{x-2}\) при выделении целой части?

1. \(y =3+\frac{1}{x-2}\)
2. \(y =3+\frac{1}{3x-5}\)
3. \(y =1+\frac{3}{x-2}\)
4. \(y =\frac{1}{x-2}\)

Задание 4.
Чему равна функция \(y =\frac{2x-4}{x+1}\) при выделении целой части?

1. \(y =2+\frac{6}{x+1}\)
2. \(y =\frac{6}{x+1}\)
3. \(y =-6+ \frac{2}{x+1}\)
4. \(y =2-\frac{6}{x+1}\)

Задание 5.
Какая функция соответствует функции с выделенной целой частью \(y=1+\frac{2}{2x+8}\)?

1. \(y =\frac{2x+10}{2x+8}\)
2. \(y =\frac{2x+8}{2x+10}\)
3. \(y =2x+10\)
4. \(y =\frac{x+10}{x+8}\)

Ответы: 1. — 2 2. — 3 3. — 1 4. — 4 5.— 1