Математика в информатике: основы и практическое применение. Часть 1

На этой странице вы узнаете

• Почему числа есть во всем?
• Как задача первоклашек связана с миром информатики?
• Как орк Петя копил монетки с помощью арифметической прогрессии?

Математика играет важную роль в информатике и является неотъемлемой частью компьютерных наук. Она обеспечивает фундаментальные основы и инструменты для разработки программного обеспечения, анализа данных и решения сложных задач в области информационных технологий. Без надлежащего понимания математических принципов и методов, уровень эффективности и качества разработки искусственного интеллекта, алгоритмов и систем обработки информации может значительно снизиться.

Эта статья представляет собой уникальную возможность расширить знания и умения в области математики и информатики, чтобы оптимизировать работу с данными и принимать обоснованные решения в информатике. Приглашаем погрузиться в мир математических основ информатики!

Числа. Арифметические операции

До начала путешествия в мир математического волшебства и информационных технологий, важно обрести надежное понимание основных арифметических операций и их роли в информатике. В этой части статьи мы познакомим вас с этими знаниями и покажем, как применяются эти знания в практике.

Но для начала вспомним основные представления о числах. 

Числа являются абстрактными понятиями, представляющими количество или размер. 

С развитием науки стали использовать десятичную систему счисления, содержащую цифры от 0 до 9. Возникновение ее было связано с количеством пальцев на руке у человека. 

Числа в первую очередь подразделяются на отрицательные и положительные.

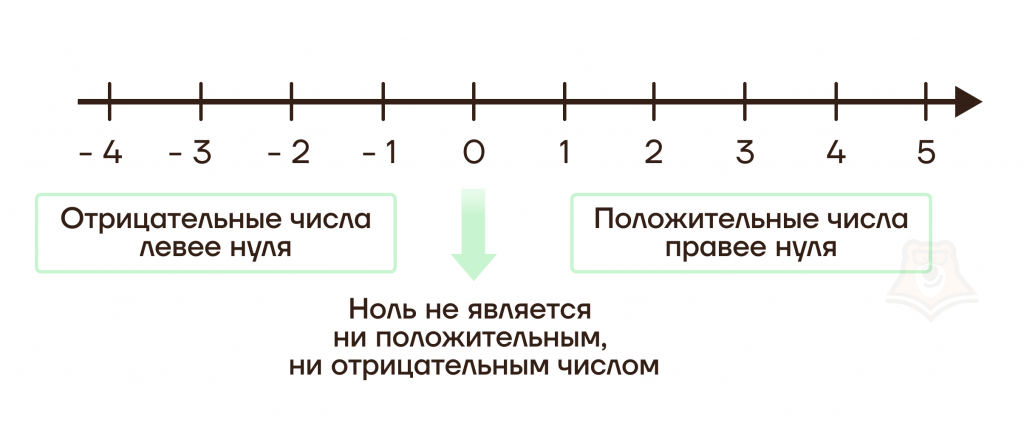
Все числа можно расставить на прямой, которая называется числовой. Отрицательные числа противоположны натуральным и находятся слева от 0 на числовой прямой.

Неположительные числа — все отрицательные числа и 0, а все неотрицательные числа — все положительные числа и 0. 

Иногда в задачах требуется не само число, а так называемый модуль.

Модуль — расстояние от любой точки на координатной прямой до начала координат. 

В математике также существуют разные множества чисел. Вспомним некоторые из них:

• Натуральные числа — числа, которые возникают при счете (1, 2, 3 и так далее). Мы используем их в повседневной жизни, чтобы посчитать количество чего-то. 
• Целые числа — группа включает в себя положительные и отрицательные числа, такие как -2, -1, 0, 1, 2)
• Рациональные числа — числа, которые можно представить в виде дробей (\(\frac{1}{2}, -\frac{3}{4}, \frac{7}{5}\) и так далее). 
• Иррациональные числа — числа, которые не могут быть представлены в виде дроби со знаменателем (такие как 𝝅 или \(\sqrt2\)). У этих чисел нет точного значения.

Также часто в математике и информатике применяется такое понятие, как вещественные числа – это объединение рациональных и иррациональных чисел.

Почему числа есть во всем? А вы знали, что математика имеет отношение и к другим наукам, например, философии? Вот несколько интересных фактов из нее: — Каждое число имеет свой смысл и обладает невероятными свойствами. Четные числа несчастливые, а нечетные счастливые. — В основе любви лежит число 5. — Число 4 совершенно, оно находится в соответствии с человеческой душой. — Первые числа 1, 2, 3, 4 означают соответственно огонь, землю, воду и воздух. Сумма этих чисел (число 10), изображает весь мир.

Понимание основных арифметических операций — сложения, вычитания, умножения и деления — является фундаментальной частью нашего путешествия. Именно они помогают нам выполнять различные действия в повседневной жизни.

• Сложение позволяет объединять два или более числа для получения их суммы. Например, сумма чисел 2 и 3 равна 5. Чтобы сложить числа, мы просто прибавляем их вместе.
• Вычитание — это обратная сложению операция. Она позволяет отнять одно число от другого. Например, если от числа 5 вычесть 2, получим 3. Вычитание также можно представить как добавление отрицательного числа. Например, \(5-2\) можно представить как \(5+(-2)\).
• Умножение — это операция, которая позволяет нам находить произведение двух чисел. Например, произведение чисел 2 и 3 равно 6. Мы можем представить умножение как повторение сложения: \(2*3\) можно рассматривать как сумму \(2+2+2\).
• Деление — это операция, обратная умножению. Она позволяет нам разделить одно число на другое. Например, если число 10 разделить на 2, получим 5. Деление также можно представить как умножение на обратное число. Например, \(\frac{10}{2}\) можно представить как \(10*\frac{1}{2}\).

Эти четыре основные арифметические операции являются неотъемлемой частью расчетов и операций в информатике. Они широко используются для решения различных задач программирования и алгоритмических проблем. Важно также иметь навыки работы с различными типами чисел и уметь применять арифметику для решения различных задач и проблем.

Но зачем же нам все эти знания? Почему эти основы так важны при изучении информатики? На эти и многие другие вопросы мы узнаем ответ далее.

Перевод текста на математический язык

В предыдущей части статьи мы изучили основные арифметические операции и познакомились с разными типами чисел. Теперь давайте перейдем к следующему шагу – переводу текстовых задач на математический язык.

Часто в информатике и математике возникает необходимость перевести словесное описание задачи в формулы или выражения, чтобы быстро и точно решить ее.  Для этого необходимо умение анализировать задачу и переводить информацию на математический язык. Это можно проследить на самой простой задаче, которую каждый первоклассник когда-то решал. 

Как задача первоклашек связана с миром информатики? Для примера рассмотрим следующую задачу, которую многие из нас решали еще в начальной школе: У Марии есть некоторое количество яблок. После того, как она отдала 3 яблока своему другу и съела еще 2 яблока, у нее осталось 7 яблок. Сколько яблок у Марии изначально? Как решить эту задачу? Конечно, используя «математический язык»! Для этого сначала прочитайте задачу внимательно и выделите ключевые слова и фразы, которые помогут определить необходимые переменные и операции. Затем установите связь между словесным описанием задачи и математическими символами. Давайте представим, что у Марии изначально было Х яблок. Затем можно выразить количество яблок, которые она отдала другу, как 3, и количество яблок, которые она съела, как 2. Используя эти переменные и операции, мы можем записать уравнение: \(X-3-2=7\) Здесь Х представляет изначальное количество яблок, 3 и 2 – количество отданных и съеденных яблок соответственно, а 7 – оставшееся количество яблок. Для решения этого уравнения можно просто сложить числа 3 и 2, а затем вычесть полученную сумму из 7: \(X-5=7\) \(X=7+5\) \(X=12\) Итак, изначально у Марии было 12 яблок. Это и будет ответом к задаче. Данный пример, несмотря на свою простоту, помогает нам осознать важность умений логически мыслить, разбивать сложные задачи на более мелкие и переводить их на понятный математический язык, как и в информатике.

Часто мы сталкиваемся с более трудными задачами, которые сначала кажутся непосильными. Однако разбиение таких задач на более простые составляющие и перевод их на математический язык значительно облегчает решение.

Практика перевода текстовых задач на математический язык поможет улучшить ваш аналитический и логический навык. Постепенно вы будете становиться более уверенными в работе с математикой и информатикой.

В информатике часто встречаются задачи, которые требуют знаний математических законов и теорем. Без них невозможно было бы решить конкретные задачи. Давайте рассмотрим основные из них.

Основные математические теоремы

Для начала предлагаем рассмотреть некоторые теоремы, а потом рассмотреть задачи, в которых эти знания можно применить.

Самые важные теоремы и основы математики, которые имеют применение в информатике:

• Неравенство треугольника – это одна из основных теорем геометрии, которая определяет условие, которому должны удовлетворять длины сторон треугольника. Она утверждает, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны.
  
  Если a, b и c — длины сторон треугольника, то неравенство треугольника можно записать следующим образом: \(a + b > c, a + c > b, b + c > a\). Эта теорема находит применение в информатике, особенно в областях компьютерной графики, алгоритмов пути и расчета расстояний.
  
  Например, даны три стороны. Требуется выяснить, образуют ли эти стороны треугольник или нет.
  
  Дано: 5, 10, 7. Необходимо применить неравенство треугольника:

\(5+10 >4, 15 >4\) — выполняется
\(5+7 >10, 12 >10\) — выполняется
\(10+7 >5, 17 >5\) — выполняется

Все три выражения выполняются, поэтому данные стороны образуют треугольник.

• Теорема Пифагора — это одна из наиболее известных теорем в математике, которая устанавливает связь между длинами сторон прямоугольного треугольника. Она утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов (других двух сторон).
  
  Математически, если a, b и c — длины сторон прямоугольного треугольника, где c является гипотенузой, то теорему Пифагора можно записать в виде \(a^2 + b^2 = c^2\). Эта теорема имеет широкую практическую применимость, включая использование в алгоритмах компьютерного зрения, геометрических вычислениях и криптографии.

Например, требуется выяснить, является ли треугольник прямоугольным или нет. 

Дано: 4, 5, 3. Для начала проверим, что данные стороны действительно образуют треугольник. Снова воспользуется неравенством треугольника:  

\(4+5 >3, 8 >3\) — выполняется
\(4+3 >5, 7 >5\) — выполняется
\(5+3 >4, 8 >4\) — выполняется

Все три выражения выполняются, поэтому стороны образуют треугольник. Теперь воспользуемся теоремой Пифагора. Вспомним, что гипотенуза — большая сторона, запишем:

\(4^2+3^2=5^2\)
\(16+9=25\)
\(25=25\)

Из этого следует, что треугольник является прямоугольным!

• Арифметическая прогрессия — это последовательность чисел, в которой каждое следующее число получается путем добавления фиксированного значения, называемого разностью, к предыдущему числу. Каждый элемент арифметической прогрессии можно записать в виде \(a, a+d, a+2d, a+3d\) и так далее, где a — начальный член, а d — разность. Арифметические прогрессии находят применение в информатике в различных областях, таких как алгоритмы сортировки, генерация числовых последовательностей и оптимизация кода.

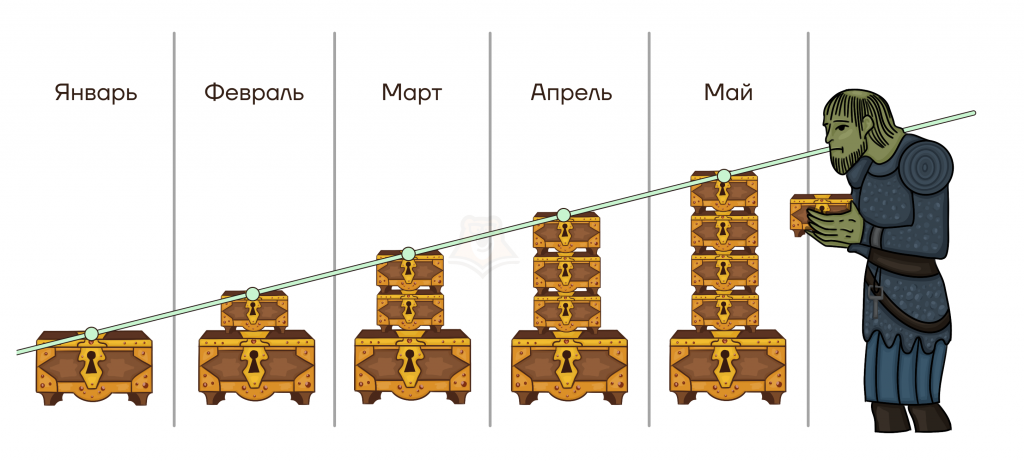
Как орк Петя копил монетки с помощью арифметической прогрессии? Рассмотрим орка Петю, который копит монетки на свою мечту. Изначально у него была одна большая шкатулка монет, которую в январе он нашел у себя дома. Затем он решил, что каждое начало месяца будет откладывать по маленькой шкатулке с монетками (одна маленькая шкатулка содержит 100 монет, а большая 200). Орк Петя хочет понять, сколько монет он накопит к концу мая? Для того, чтобы решить данную задачу, необходимо вспомнить основные формулы для арифметической прогрессии (на картинке ниже).  Нам необходимо воспользоваться первой формулой, чтобы выяснить, какую сумму он накопит к концу мая. Петя начал копить в январе — это первый месяц, а май — 5. То есть у нас будет 5 членов арифметической прогрессии. Если посмотреть на первую формулу, то как раз по ней мы можем найти n член прогресии: \(a_n=a_1+(n-1)*d\) \(a_5=200+(5-1)*100\) \(a_5=200+4*100=200+400=600\) То есть в к концу мая он отложит уже 600 монет!

• Пропорции — это математическая концепция, которая связывает соотношение между различными значениями или величинами. Они используются для сравнения двух или более наборов данных и определения связи их друг с другом.
  
  Пропорции обычно записываются в виде: \(\frac{a}{b}=\frac{c}{d}\), где a, b, c и d представляют различные числа или величины. Левая и правая части пропорции должны иметь одно и то же значение или отношение.
  
  Для чтения пропорции вы можете использовать фразу «a относится к b, как c относится к d» или «a разделить на b равно c разделить на d». Например, если у нас есть пропорция \(\frac{2}{4}=\frac{6}{12}\), мы можем прочитать ее как «2 относится к 4, как 6 относится к 12» или «2 разделить на 4 равно 6 разделить на 12».
  
  Например, дана такая задача: рабочий за 2 дня копает 10 кг картошки. Сколько килограммов картошки он выкопает за 10 дней, если будет работать с такой же скоростью?
  
  Разумеется, данная задача легкая, но она хорошо демонстрирует правила пропорций. Давайте составим математическую модель или переведем текст на математический язык. Обозначим за X неизвестное.

2 дня — 10 кг картошки
10 дней — X кг картошки

Составим пропорцию: \(\frac{2}{10}=\frac{10}{X}\). По правилам математики найдем X:

\(2*X=10*10\)
\(X=\frac{10*10}{2}=\frac{100}{2}=50\)

За 10 дней рабочий выкопает 50 кг картошки. Это и будет ответом. 

Теперь, когда мы рассмотрели основы математики, которые обязательно пригодятся нам в информатике, настало время обратить внимание на числа и их свойства.

Числа. Делимость чисел

Делимость чисел является математической концепцией, которая позволяет нам анализировать и классифицировать числа на основе их взаимоотношений.  Делимость и неделимость — это понятия, связанные с возможностью деления чисел на другие числа без остатка.

Делимость относится к ситуации, когда одно число делится на другое число без остатка. То есть, если число «a» делится на число «b» без остатка, мы говорим, что «a» делится на «b» или «b» является делителем «a». Это означает, что «a» можно разделить на «b» на равные части.

Хорошим началом для изучения делимости чисел является знание условий, которые сделают число делимым на другое число без остатка. Например:

• Число делится на 2, если его последняя цифра является четной (либо же говорят, что четное число делится на 2).
• Число делится на 5, если его последняя цифра равна 0 или 5. 
• Число делится на 3, если если сумма цифр делится на 3. 
• Другие примеры включают условия делимости на 4, 6, 9 и 10, на этом подробнее останавливаться мы не будем.

Из этих условий вытекает понятие натуральных делителей числа.

Натуральные делители числа — это числа, на которые заданное число делится без остатка.

Например, делителями числа 10 являются 1, 2, 5 и 10. 

Можно заметить, что каждое число в списке своих натуральных делителей точно будет иметь 1 и себя, в данном случае 10. 

Числа, которые делятся без остатка только на 1 и на себя, называются простыми числами. 

Простые числа имеют только два различных натуральных делителя: 1 и само число. 

Это же понятие помогает при решении задач, так как появляется другой термин.

Нетривиальные делители — это делители числа, отличные от 1 и самого числа.

Как же проверить числа на простоту?

• Убедитесь, что число больше 1. Простые числа должны быть больше 1.
• Проверьте, делится ли число на любое число, кроме 1 и самого себя. Для этого пройдите по всем числам в интервале от 2 до корня из проверяемого числа (почему именно так – читайте в статье «Практика оптимального программирования. Поиск делителей числа») и проверьте, делится ли оно на одно из этих чисел без остатка. Если число делится на какое-либо число без остатка, оно не является простым. В противном случае, оно является простым числом.

Если вы уже знакомы с Python, то этот алгоритм можно перенести в код, чтобы в дальнейшем использовать в задачах! Но если вы ни разу не сталкивались с программированием, то приглашаем вас в статью «Основы программирования на языке Python».

Сделаем важное замечание про остаток от деления у отрицательного числа. При решении задач иногда приходится сталкиваться с подобными ситуациями. Когда мы имеем дело с отрицательным числом и вычисляем остаток от деления, результат может быть несколько отличаться в зависимости от используемого языка программирования или математических правил. В таких случаях важно понимать, как ваша система округления решает эту проблему.

В Python для правильного нахождения остатка от деления у отрицательного числа необходимо взять модуль: a = -1000 b = 45 print(abs(a) % b) # 10 — верный ответ print(a % b) # 35 — неверный ответ

Более подробно работа с делителями рассмотрена в статье «Практика оптимального программирования. Поиск делителей числа». Так что если вы хотите глубже погрузиться в эту важную тему информатики, то приглашаем в мир делителей!

Потренируемся применять полученные навыки на примере задачи 25 номера ЕГЭ!

Задание. Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [245721 ; 245801] простые числа. Выведите на экран все найденные простые числа в порядке возрастания. Каждое число должно быть выведено в отдельной строке.

Решение.
1. Воспользуемся алгоритмом, предложенным выше. Очевидно, что числа у нас больше 1, поэтому условие можно не проверять. Далее нам необходимо будет перебрать каждое число:

for i in range(245721,245801+1):

2. Будем перебирать от 2 до квадратного корня. Необходимо его найти, используя конструкцию:

kv_koren=int(i**0.5)

3. Введем переменную flag. Она будет отвечать за то, простое число или нет. В чем смысл? Изначально она равна 1. Если мы встречаем хотя бы один делитель, то сразу присвоим значение 0 и дальше не будем осуществлять проверку на простоту, ибо смысла в этом нет:

flag=1

4. Далее начнем перебирать делители от 2 до квадратного корня, найденного ранее:

for delitel in range(2,kv_koren+1):

5. Если нашелся делитель, то значению flag присваиваем значение 0 и делаем break, так как данное число уже не является простым:

 if i%delitel==0:
      flag=0
      break

6. Когда прошлись по всем делителям или вышли из цикла, проверяем значение flag. Если оно осталось таким же, то есть равным 1, число является простым, мы его выводим:

if flag==1:
        print(i)

Полный код программы:

for i in range(245721,245801+1):
          kv_koren=int(i**0.5)
          flag=1

          for delitel in range(2,kv_koren+1):
               if i%delitel==0:
                  flag=0
                  break
          if flag==1:
                 print(i)

Рассмотрим не менее интересную часть про делимость чисел, которую вы наверняка затрагивали в школе… Иногда приходится работать с суммами, разностями чисел, а также их  произведением. При этом необходимо уметь работать с их остатками и делителями.

• Если каждое слагаемое суммы двух чисел делится без остатка на некоторое число, то и сумма этих чисел делится на это число. 
  
  Пример: 24+6=30
  Число 24 делится на 1, 2, 3, 4, 6, 8, 24.
  Число 6 делится на 1, 2, 3, 6.
  
  Общие делители у этих чисел: 1, 2, 3, 6. То есть сумма должна делиться на 1, 2, 3, 6. Число 30 как раз делится на эти числа.

• Если каждое слагаемое разности двух чисел делится без остатка на некоторое число, то и разность этих чисел делится на это число.
  
  Пример: 24-6=18
  Число 24 делится на 1, 2, 3, 4, 6, 8, 24.
  Число 6 делится на 1, 2, 3, 6.
  
  Общие делители у этих чисел: 1, 2, 3, 6. То есть сумма должна делиться на 1, 2, 3, 6. Число 18 как раз делится на эти числа.

• Если один из множителей произведения двух чисел делится на некоторое число, то и произведение делится на это число
  
  Пример: 12*3=36
  
  По сути 12 и 3 мы можем разложить на  делители:
  12=1*4*3
  3=1*3
  
  4*3*3=36
  
  Как мы можем увидеть, число 36 делится на 4, 3, 9, 2 и т.п. То есть можно всегда разложить числа на более мелкие произведения, поэтому если множитель делится на какое-либо число, то и произведение также делится на это число. 

Со временем в математике появились два брата — НОД и НОК! 

НОД (наибольший общий делитель) двух чисел – это наибольшее число, которое делит оба числа без остатка.

НОК (наименьшее общее кратное) двух чисел – это наименьшее число, которое делится на оба числа без остатка.

Что же это такое и как это найти? 

Алгоритм нахождения НОК:

Шаг 1. Разложить два числа на простые множители.
Шаг 2. Выписать разложение одного из двух чисел.
Шаг 3. Дописать недостающие множители другого.
Шаг 4. Вычислить полученное произведение.

Пример нахождения НОК: возьмем два числа – 24 и 60. 

1. Разложим их на простые множители:

24=2*2*2*3
60=5*2*2*3

2. Выпишем разложение числа 24 и допишем недостающие множители другого:
   
   Множители 24: 2 2 2 3
   Множители 60: 2 2 3 5
   
   Допишем множители 24 к 60: 2 2 3 2 5

3. Перемножим: 2*2*3*2*5=120. НОК(24,60)=120. Это и будет ответом!

Алгоритм нахождения НОД:

Шаг 1. Разложить два числа на простые множители.
Шаг 2. Найти общие множители в полученных разложениях.
Шаг 3. Найти их произведение.

Пример нахождения НОД: возьмем два числа — 24 и 60. 

1. Разложим их на простые множители:

24=2*2*2*3
60=5*2*2*3

2. Найдем общие множители (зеленым цветом):

Множители 24: 2 2 2 3
Множители 60: 2 2 3 5

Получим: 2 2 3

3. Перемножим: 2*2*3=12. НОД(24,60)=12. Это и будет ответом!

Потренируемся применять полученные навыки на примере другого типа задачи 25 номера ЕГЭ!

Задание. Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [210 200; 210 300], числа, имеющие ровно четыре различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти четыре делителя в четыре соседних столбца на экране с новой строки. Делители в строке должны следовать в порядке возрастания.

Решение.

1. Воспользуемся алгоритмом, о котором мы говорили уже выше. Нам необходимо будет перебрать каждое число:

for i in range(210200,210300+1):

2. Для того, чтобы сохранять значения делителей, будем использовать множество. Так как оно будет содержать неповторящиеся элементы. Это поможет избежать добавления делителей, которые мы уже учли.

a = set()

3. Будем перебирать делители от 2 до квадратного корня. Необходимо их найти, используя конструкцию:

for k in range(2,int(i**0.5)+1):

4. Если мы нашли такое число (делитель), которое нацело делится на наше исходное число, для которого мы ищем делители, то добавляем его в множество. А также добавляем целую часть от деления, так как это число также будет являться делителем.

if i%k==0:
            a.add(k)
              a.add(i//k)

5. Когда мы проверили все числа, то нужно проверить, сколько делителей мы получили в итоге. Если количество делителей 4, как в условии, то мы сортируем множества по возрастанию чисел, а затем выводим все делители.

if len(a)==4:
            print(*sorted(a))

Полный код программы:

for i in range(210200,210300+1):
           a = set()

           for k in range(2,int(i**0.5)+1):
                       if i%k==0:
                                   a.add(k)
                                   a.add(i//k)
           if len(a)==4:
                       print(*sorted(a))

Разумеется, эту задачу можно решить и другим способом. Например, используя списки в Python, но подробнее на этом останавливаться мы не будем. 

В этой части статьи мы познакомились с некоторыми основами математики, которые необходимы при изучении информатики. Приглашаем продолжить изучение этой интересной темы во второй части статьи «Математика в информатике: основы и практическое применение. Часть 2»!

Термины

Гипотенуза — в геометрии гипотенузой называется сторона прямоугольного треугольника, которая расположена напротив прямого угла. Она является наибольшей стороной прямоугольного треугольника.

Катет — в геометрии катетами прямоугольного треугольного называются две стороны, которые образуют прямой угол. Они являются меньшими сторонами по сравнению с гипотенузой.

Обратное число — это число, которое при умножении на исходное число дает результат, равный 1.

Переменные —  в математике это символы или буквы, которые используются для представления неизвестных или меняющихся значений. Они обычно обозначаются буквами, такими как x, y, a, b и т.д.

Простые множители — это числа, которые делят данное число без остатка и не могут быть разложены на множители, отличные от самих себя и единицы.

Фактчек

• При обработке текста, содержащего математические концепции, важно уметь переводить его на математический язык.
• Арифметические операции включают сложение, вычитание, умножение и деление чисел. Эти операции выполняются с различными типами чисел, такими как вещественные, целые, положительные и отрицательные числа.
• Важно знать основные математические теоремы, такие как неравенство треугольника и теорема Пифагора.
• Умение решать уравнения и неравенства помогает в анализе и представлении математических проблем.
• Раздел делимость чисел объясняет условия делимости чисел, процесс проверки чисел на простоту, а также понятия НОД (наибольший общий делитель) и НОК (наименьшее общее кратное).

Проверь себя

Задание 1.
Какой из перечисленных типов чисел включает все натуральные числа и ноль?

1. Вещественные числа
2. Целые числа
3. Положительные числа
4. Неотрицательные числа

Задание 2.
Какое из следующих утверждений лучше всего описывает пропорцию в математике?

1. Пропорция — это соотношение двух или более величин, которые остаются пропорциональными даже при изменении их значения.
2. Пропорция — это процесс умножения двух чисел.
3. Пропорция — это отношение одной величины к другой, которое может быть выражено в виде десятичной дроби.
4. Пропорцию можно использовать только в геометрии, чтобы вычислить длину стороны треугольника.

Задание 3.
Какая теорема устанавливает соотношение между длинами сторон прямоугольного прямоугольника?

1. Теорема Виета
2. Теорема Ферма
3. Теорема Пифагора
4. Теорема Аполлония

Задание 4.
Какое математическое понятие описывает счетчик, увеличивающийся или уменьшающийся на одно и то же число?

1. Арифметическая прогрессия
2. Геометрическая прогрессия
3. Арифметическое среднее
4. Геометрическое среднее

Задание 5.
Как называется операция, которая определяет, сколько раз одно число содержится в другом?

1. НОД (наибольший общий делитель)
2. НОК (наименьшее общее кратное)
3. Деление с остатком
4. Простое число

Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.