Математика для физики

На этой странице вы узнаете

• Почему теория физики Аристотеля оказалась несостоятельной?
• Почему физики так любят векторы?
• Что нужно знать, чтобы правильно спланировать путешествие?

Справедливость любой физической теории подтверждается экспериментально. 

Наблюдая за явлениями природы, можно получить истинное наслаждение! Насколько красивы водопады и морской прибой. Как могут восхищать вспышки молнии или пугать солнечные затмения. Но наблюдения не всегда позволяют проникнуть в суть явления. Великие открытия делаются исключительно любопытными людьми, для которых вопрос «Почему?» становится смыслом жизни.  

Только экспериментируя и анализируя результат эксперимента, можно понять суть явления! А для анализа нам как раз пригодится математика. 

Как вычисляют физики

Физические величины имеют столь разнообразные значения, что измерение их требует уникальной точности. Как можно измерить массу электрона, заряд протона или массу Юпитера?

Человечеству просто необходимо умение действовать с малыми или огромными числами. Приведение числовых значений в стандартном виде значительно облегчает вычисление. Например, мы можем представить очень маленькое или очень большое значение в стандартном виде числа.

Стандартный вид числа — это запись числа в виде произведения: x*10ⁿ, где 1 ⩽ x < 10, n — целое число. 

Элементарный электрический заряд: \(е = — 0,00000000000000000000000016 = — 1,6*10^{-19}\)Кл Масса Земли: \(М=6000000000000000000000000 = 6*10^{24}\) кг

Но зачем нам это нужно? Действия с показательными выражениями помогут получить верный числовой ответ, что значительно облегчает работу с числами.

Рассмотрим пример задачи, в которой необходимо провести расчет с использованием свойств показательных выражений, задание № 5 ОГЭ по физике.

Задание. Земля имеет массу \(М_з=6*10^{24}\) кг, а Солнце — \(M_c=2*10^{30}\) кг. Определите силу взаимного притяжения этих космических тел, если они находятся на расстоянии r = 150 млн км. Гравитационная постоянная

\(G = 6,67*10^{-11}\frac{Н*м^2}{кг^2}\).

Решение. По закону всемирного тяготения: 

\(F=G\frac{М_зМ_с}{r^2}\)

Вычислим: 

\(F=\frac{6,67*10^{-11}*6*10^{24}* 2*10^{30}}{(1,5 * 10^{11})^2}= 35,5*10^{21}\) (H).

Ответ: \(35,5 *10^{21}\)

Заметим, что решение задачи основано на формуле, являющейся математическим выражением закона. Наши гениальные предки в процессе длительного изучения явлений, осмысливания результатов эксперимента пришли к законам, которые описывают природные явления. А эти законы записали с помощью переменных. 

Почему теория физики Аристотеля оказалась несостоятельной? Основоположником науки о природе — физики — считается Аристотель (384—322 годы до нашей эры). Этот гениальный человек отличался наблюдательностью и глубокими аналитическими способностями. Его желание объяснить суть наблюдаемых природных явлений достойно восхищения! Однако ни одно утверждение Аристотеля, главенствующее в науке в течение двух тысячелетий, не получило своего подтверждения. Только экспериментальное подтверждение любой гипотезы превращает ее в теорию. Опытным путем доказать утверждения философа было невозможно.  Например, Аристотель отрицал возможность пустоты. Он утверждал, что любой элемент пространства заполнен материей. Связь скорости движения тела с плотностью среды, в которой оно движется, предполагает бесконечно большую скорость в вакууме. Сейчас мы знаем, что скорость тела не зависит от плотности пространства. Более того, скорость тела в космическом пространстве может оставаться постоянной.

Формулы в физике

Физические величины, количественно характеризующие протекание явления, записанные в виде переменных, составляют математическую запись закона, которую мы называем формулой. Теперь нам нет необходимости их снова выводить. Достаточно взять готовую и применить ее.

Часто приходится выражать зависимость величины, входящей в состав формулы. Ведь задачи по физике решаются именно благодаря расчетным формулам.

Рассмотрим задачу по определению плотности вещества — задание  №24 ОГЭ по физике.

Задание. Медный однородный куб с ребром a разрезают, удалив из него кубик с ребром \(\frac{a}{2}\). Эту часть заменят кубиком, изготовленным из материала, плотность которого в 2 раза меньше. Плотность меди 8600 кг/м³. Определите среднюю плотность полученного составного куба.

Решение. Плотность составного куба: \(\rho=\frac{m}{V}\), где \(m=m_1+m_2\) — масса составного куба, \(V=a^3\)— его объем.

Масса меди в кубе:

\(m_1=\rho_1(V-V_1)=\rho_1(a^3-\frac{a^3}{8})=\frac{7\rho_1a^3}{8}\).

Масса материала плотностью \(\rho_2=\frac{\rho_1}{2}\) составляет \(m_2 =\rho_2\frac{a^3}{8}=\frac{\rho_1a^3}{16}\).

Получим: 

\(\rho=\frac{\frac{7\rho_1a^3}{8}+\frac{\rho_1a^3}{16}}{a^3}=\frac{15\rho_1}{16}=8062,5 (кг/м^3)\)

Ответ: 8062,5

Обратим внимание, что в этом примере мы воспользовались математической формулой определения объема куба. При решении задач ограничиваться только физическими формулами не получается. Такие величины, как объем тела, площадь фигуры можно определить, обратившись к формулам геометрии.

Останавливаться на всех формулах мы не будем, но вспомним основные из них. 

Физическая величина	Формула	Величины в формуле
Площадь прямоугольника	\(S=ab\)	\(a,b\) — стороны прямоугольника
Площадь круга	\(S=\pi r^2\)	\(r\) — радиус окружности
Объем прямоугольного параллелепипеда	\(V=abc\)	\(a,b,c\) — стороны прямоугольного параллелепипеда
Объем шара	\(V=\frac{4}{3}\pi r^3\)	\(r\) — радиус шара

Системы уравнений в решении задач

К сожалению, бывает так, что применение только одного закона не приводит к верному решению. Возникает необходимость составления и решения системы уравнений. 

Система уравнений – это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует одновременно всем данным уравнениям. 

Систему уравнений можно решить несколькими способами:

• графически;
• методом подстановки;
• методом алгебраического сложения. 

Подробнее про каждый из способов решения системы вы можете прочесть в статье, на которую мы ссылались выше. 

Рациональным будет то решение, которое потребует наименьшего времени. Без навыка решения систем уравнений в математике здесь не обойтись.

Примером может служить решение задачи №25 ЕГЭ по физике.

Задание. ЭДС источника тока определяют, измеряя силу тока, протекающего в цепи. Если к источнику тока подключить лампу, сопротивление которой составляет 110 Ом, то сила тока в цепи равна 1 А. Ток короткого замыкания — 10 А. Чему равна ЭДС источника по результатам эксперимента? 

Решение. По закону Ома для полной цепи: \(I_1=\frac{\xi}{R+r}\), где \(\xi\) — ЭДС источника тока, внутреннее сопротивление которого r.

В случае короткого замыкания \(R\rightarrow 0\), имеем: \(I_2=\frac{\xi}{R}\).

Составим систему уравнений:

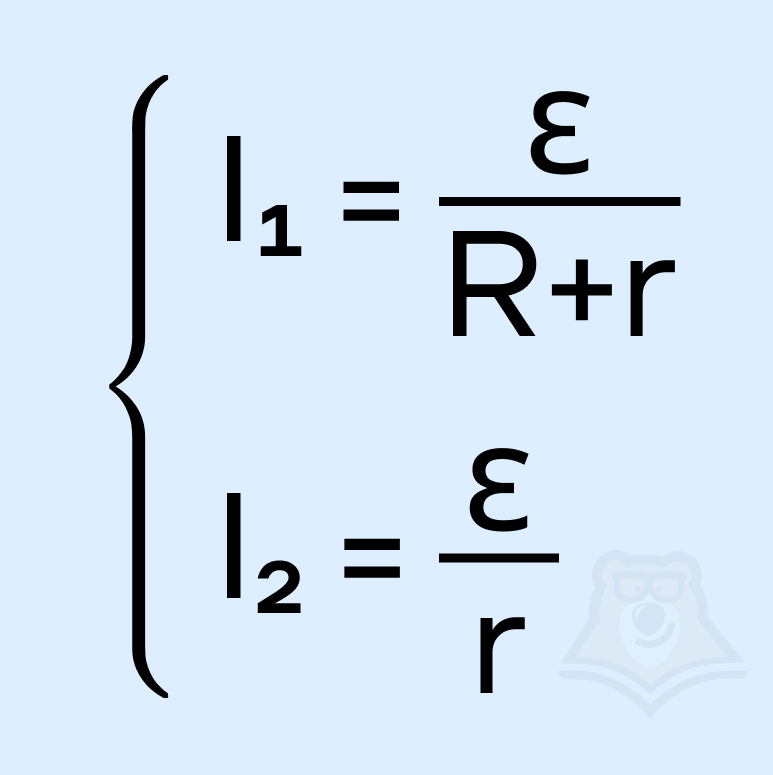
Преобразуем систему:

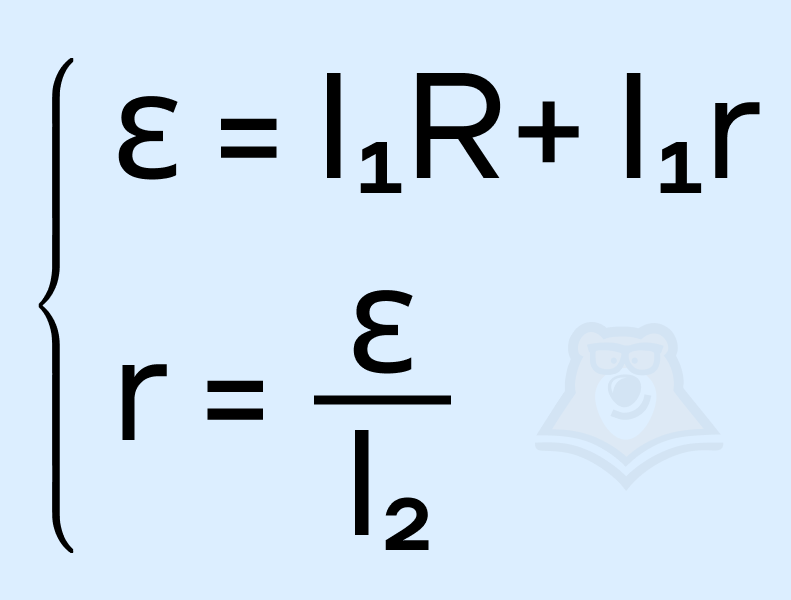
Подставим второе уравнение системы в первое:

\(\xi=I_1R+I_1\frac{\xi}{I_2}|*I_2\)
\(I_2\xi=I_1I_2R+I_1\xi\)
\(\xi=\frac{I_1I_2R}{I_2-I_1}\).

Вычислим: 

\(\xi=\frac{110*1*10}{11}=100 (В)\).

Ответ: \(100\)

Нельзя не вспомнить, что физические величины могут быть скалярными и векторными. 

Применение векторов

Зависимость значения физической величины от направления представлена с введением векторов. 

Вектором мы будем называть направленный отрезок прямой. 

Модуль вектора — длина соответствующего отрезка. 

Векторы могут быть сонаправленными (то есть направленными в одну сторону), или направление их будет отличаться. 

Если векторы параллельны одной прямой, то их называют коллинеарными.

В процессе изучения движения вдоль одной прямой понятие коллинеарных векторов значительно облегчает жизнь физикам. 

Направления векторов могут в этом случае быть как совпадающими, так и противоположными. Сложить такие векторы можно с применением понятия проекции на ось координат, параллельную направленным отрезком. 

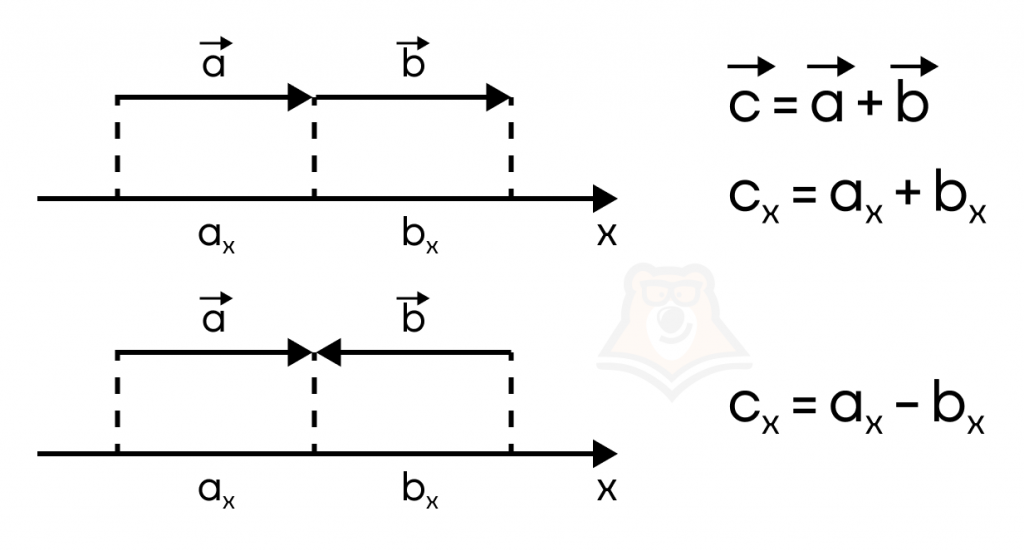
Заметим, что под проекцией в этом случае следует понимать отрезок на оси координат, образованный перпендикулярами восстановленными из начала и конца вектора к координатной оси.

Различия в направлении при этом будут очевидны, поскольку проекция вектора, направленного против оси, отрицательна.

В более сложной ситуации, когда векторы направлены под углом друг к другу, можно применить это же правило. Необходимость сложения таких разнонаправленных величин приводит к применению правил треугольника и параллелограмма.

Сложение векторов

На экзамене по физике встречаются геометрические задачи. В них ответом служит вектор, значение которого — сумма векторных величин.

Сложить или вычесть векторы можно с помощью:

• правила треугольника;
• правила параллелограмма;
• правила многоугольника. 

Правило треугольника: геометрической суммой векторов, при совпадении конца первого вектора с началом второго является вектор, соединяющий начало первого и конец второго.

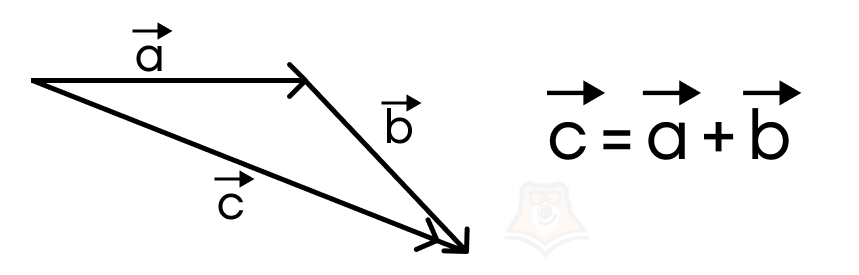
Удобно применять это правило для векторов, параллельный перенос которых не меняет суть задачи. При вычитании аналогичных векторов необходимо сложить первый с вектором, противоположным второму.

В физике чаще всего применяется правило параллелограмма.

Правило параллелограмма: геометрической суммой векторов, исходящих из одной точки, является диагональ параллелограмма, проведенная из этой же точки. Параллелограмм достраивается с помощью параллельного переноса векторов.

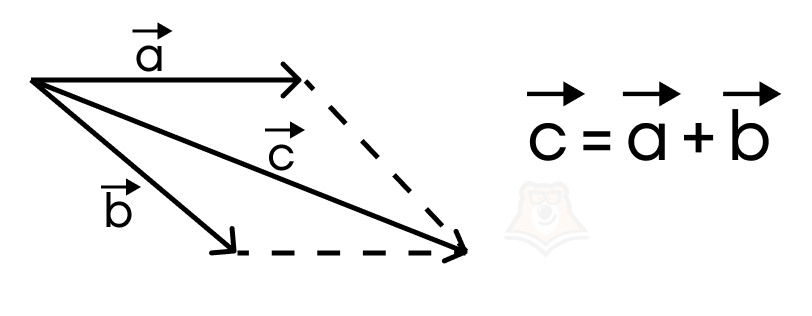
Мы кратко вспомнили основные понятия в теме векторов, но на правилах треугольника и многоугольника, а также более узких свойствах вектора мы останавливаться не будем. Если вам интересно освежить в памяти теорию, то вы можете прочесть наши статьи:

• Векторы. Часть 1
• Векторы. Часть 2

Рассмотрим пример задачи из ЕГЭ по физике № 2, в которой как раз применяется правило параллелограмма.

Задание. Три силы, векторы которых представлены на рисунке, приложены к одной точке и лежат в одной плоскости. Модуль вектора силы F₁ равен 5 Н. Определите модуль равнодействующей сил F₁, F₂ и F₃? (Ответ дайте в ньютонах.)

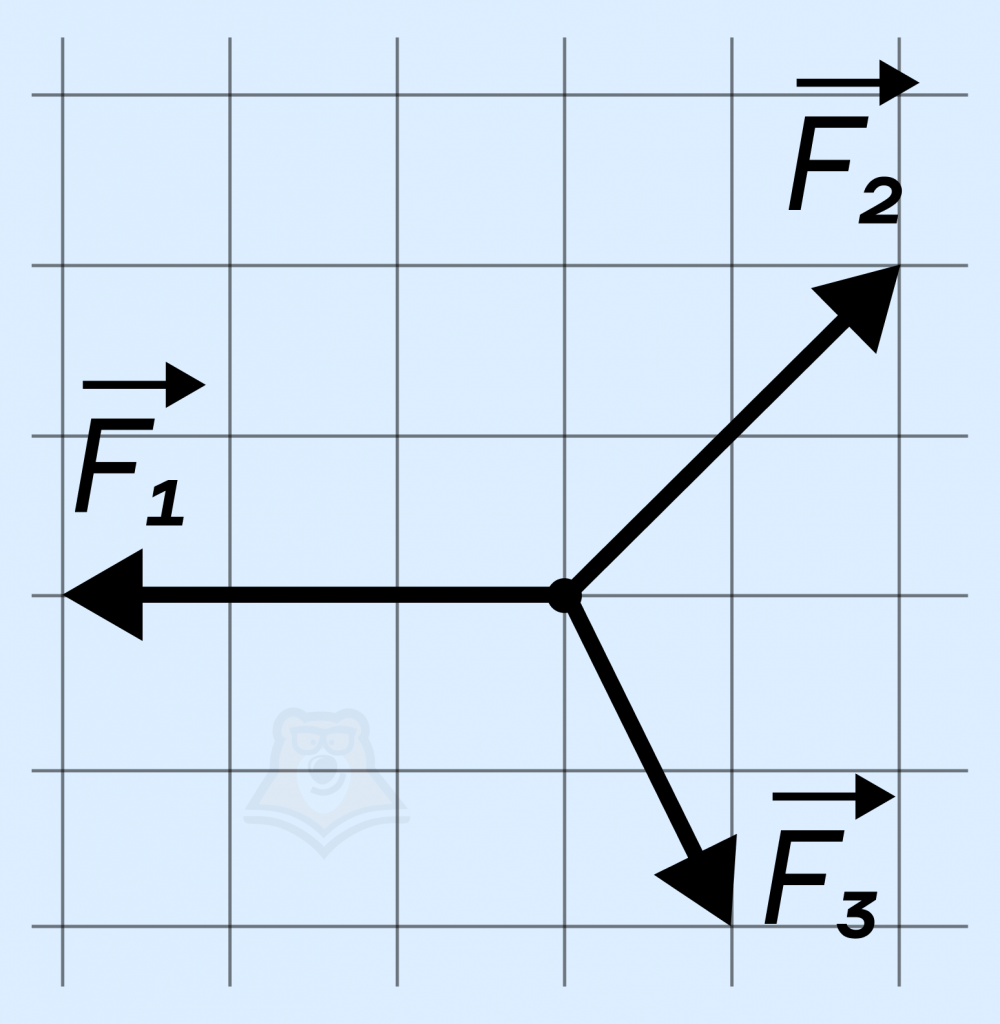
Решение. Равнодействующая равна геометрической сумме сил, действующих на тело.

На основании правила параллелограмма найдем геометрическую сумму векторов F₂ и F₃:

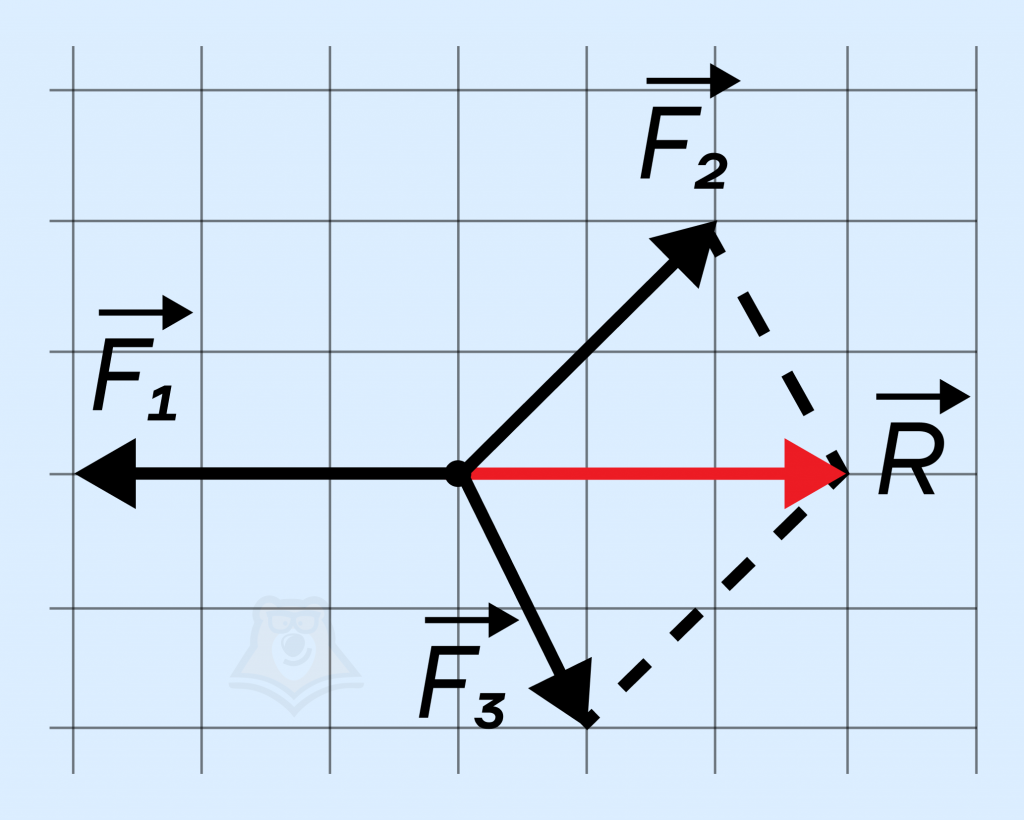
\(\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{R}\).

По рисунку очевидно, что \(\overrightarrow{F_1}=-\overrightarrow{R}\).

Их геометрическая сумма равна нулю.

Ответ: \(0\)

Почему физики так любят векторы? Как можно пояснить, что автомобиль движется не только с какой-то скоростью, но и в определенном направлении? Каким образом следует указать направление действия силы? Эти и многие другие вопросы помогают решать векторы, поэтому они и являются излюбленным инструментом физиков.

Как часто нам говорят, что мы должны знать куда идем! Если твой жизненный вектор четко определен, то и двигаться в этом направлении просто и интересно! 

Теорема Пифагора 

Если векторы направлены под углом 90^°, то модуль их суммы можно определить при помощи теоремы Пифагора.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов треугольника.

\(c^2=a^2+b^2\)

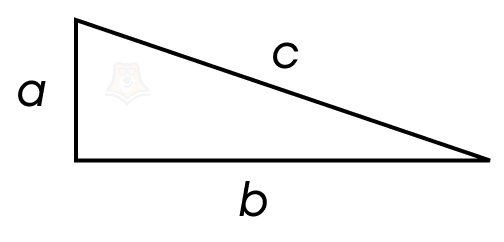
Подробнее о теореме Пифагора и способах решения задач с ее применением можно прочитать в статье:

• Равнобедренный, равносторонний и прямоугольный треугольник

Примером может служить задача на применение классического закона сложения скоростей в ЕГЭ по физике № 1.

Задание. При переправе через реку, скорость течения которой 3 м/с, необходимо перемещаться таким образом, чтобы расстояние, пройденное лодкой, было кратчайшим. Скорость лодки в стоячей воде 4 м/с. Определите скорость лодки относительно берега.

Решение.

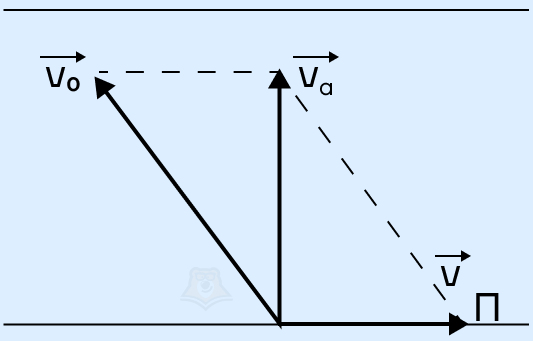
Путь будет кратчайшим, если лодка будет держать курс под углом α к берегу. Абсолютная скорость лодки направлена перпендикулярно берегу.

По закону сложения скоростей: \(\overrightarrow{v_a}=\overrightarrow{v_o}+\overrightarrow{v_п}\).

Применим теорему Пифагора: \(v_a=\sqrt{v^2_o-v^2_п}=\sqrt{3^2+4^2}=5\) (м/с).

Ответ: \(5\)

Что нужно знать, чтобы правильно спланировать путешествие? Как здорово путешествовать на собственном автомобиле! Все красоты природы тебе доступны в любое время.  Чтобы получить удовольствие от поездки, нужно многое знать и планировать: построить маршрут, предусмотреть расход топлива, запастись достаточным количеством припасов. Например, юмористическая повесть Джерома Джерома «Трое в лодке, не считая собаки» как практическое руководство просто бесценна!  А в жизни знания физики и математики могут сделать путешествие незабываемым.

Мы рассмотрели основные математические операции и формулы, позволяющие физикам не только объяснить суть явлений, но и построить математическую модель. Знание математики во много раз повышает степень понимания физики.

Подробнее о математических формулах в физике можно узнать в статье «Введение в кинематику. Относительность движения».

Термины

Переменная — буквенное обозначение элемента множества.

Фактчек

• Степенные выражения позволяют проводить расчеты как очень маленьких, так и очень больших физических величин.
• Системы уравнений дают возможность искать и находить математическую связь между физическими величинами при решении расчетных задач.
• Векторы дают возможность качественно описать физические величины, зависящие от направления. Для сложения векторов применяют правила треугольника и параллелограмма.
• Теорема Пифагора — незаменимый инструмент, использующийся при определении значений векторных физических величин, являющихся суммой векторов.

Проверь себя

Задание 1.
В каком случае запись числа в стандартном виде сделана правильно?

1. \(0,0000023 = 2,3 * 10^6\)
2. \(0,0000023 = 2,3 * 10^{-6}\)
3. \(0,0000023 = 2,3 * 10^{-5}\)
4. \(0,0000023 = 2,3 * 10^{5}\)

Задание 2.
Закон Ома для полной цепи записан в виде формулы \(I=\frac{E}{R+r}\)? В каком случае внутреннее сопротивление источника тока \(r\) выражено верно?

1. \(r=\frac{E}{R+I}\)
2. \(r=\frac{R}{E+I}\)
3. \(r=\frac{E-IR}{I}\)
4. \(r=\frac{EI-R}{I}\)

Задание 3.
Плотность вещества выражается формулой \(\rho=\frac{m}{V}\). Объем прямоугольного параллелепипеда можно определить по формуле \(V = abc\). Решив систему уравнений, запишите формулу расчета высоты \(с\).

1. \(c=\frac{m}{ab\rho}\)
2. \(c=\frac{m\rho}{ab}\)
3. \(c=\frac{\rho ab}{m}\)
4. \(c=\frac{\rho}{mab}\)

Задание 4.
Два вектора, модули которых равны 4 см и 3 см, направлены под углом 90^o друг к другу. Определите сумму этих векторов.

1. 3 см
2. 4 см
3. 5 см
4. 7 см

Задание 5.
Давление твердого тела на опору зависит от площади опоры. Из предложенных выражений выберите формулы определения площади прямоугольника.

1. \(a^2\)
2. \(\pi r^2\)
3. \(\frac{1}{1}absin\alpha\)
4. \(abc\)

Ответы: 1. – 1; 2. – 3; 3. – 1; 4. – 3; 5. – 1.