Силы электромагнитного взаимодействия в механике
На этой странице вы узнаете
- Гуттаперчевый – это хорошо или плохо?
- Как первый номер стал «осиновым колышком» на ЕГЭ 2022?
- Почему сила трения нам не враг?
Как вы думаете, почему человек до сих пор не смог создать вечный двигатель? Все из-за постоянного присутствия разных внешних факторов, которые еще называют неидеальными. Их огромное множество. Одним из них является сила трения. Но задумывались ли вы, что она из себя представляет? Или как сила упругости не дает нам «развиваться»? Сейчас обо всем этом и поговорим.
Сила упругости
Сначала остановимся на силах электромагнитной природы. Наибольшее влияние на механическое движение оказывают всего две: сила упругости и сила трения.
Сила упругости — сила, возникающая при деформации тела (при изменении его формы или размеров) и стремящаяся вернуть его к исходному состоянию.
Благодаря действию этой силы, деформированные тела принимают свою изначальную форму. Заметим, что не все тела на это способны: наряду с упругими телами (футбольный мяч, пружина) существуют пластичные тела (пластилин, смола), которые не способны самостоятельно восстановить свою форму после прекращения действия внешних сил.
Материалом, который сочетает в себе и упругие, и эластичные свойства, является гуттаперча — это смола, похожая на каучук, добываемая из растения «pertja».
| Гуттаперчевый — это хорошо или плохо? В зависимости от температуры этот материал имеет либо эластичные свойства — то есть хорошо растягивается и принимает нужную форму, либо упругие свойства — то есть при растяжении возвращается в свое исходное положение. Поэтому гуттаперчу применяют в стоматологии при пломбировании каналов — внешне она очень по цвету похожа на кожу. Прилагательное «гуттаперчевый» стало нарицательным после выхода произведения Д. В. Григоровича «Гуттаперчевый мальчик» и означает «очень гибкий». Так чаще всего говорят про юных гимнастов, которые легко могут выполнять разные упражнения, требующие большой гибкости. |
Деформация тел
Давайте разберемся, почему некоторые тела могут деформироваться, а некоторые не могут. Рассмотрим кристаллическую решетку твердого тела (именно у таких тел и возникает сила упругости).
В кристалле атомы упорядочены, то есть у каждого атома есть свое место, которое сохраняется благодаря скомпенсированному действию сил притяжения и отталкивания между всеми атомами вещества.

Вот так можно представить себе кристаллическую решетку:
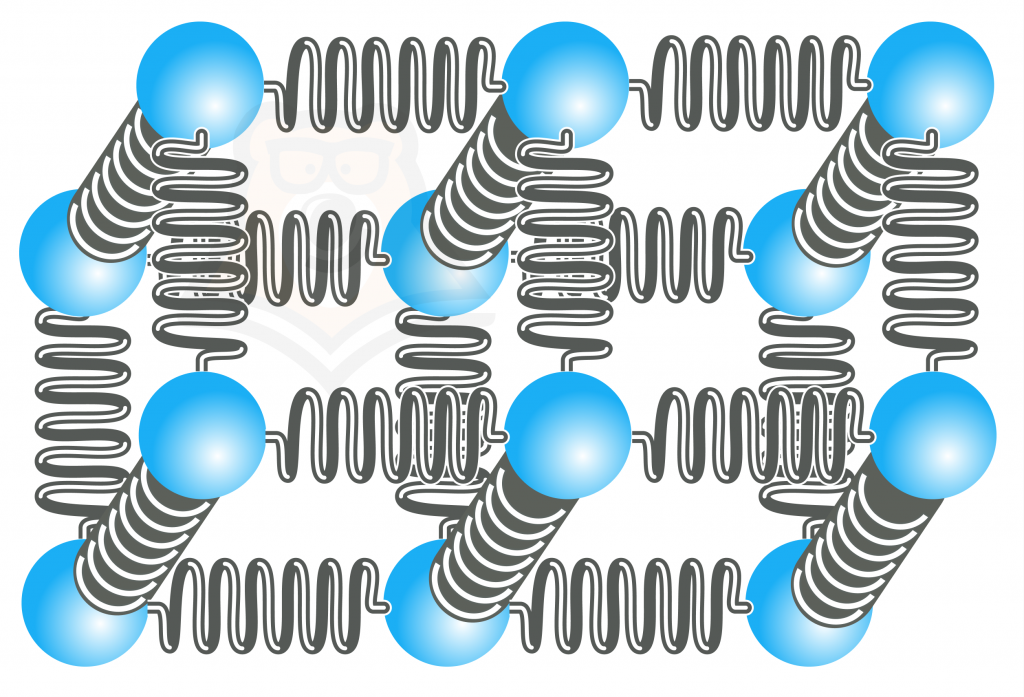
Представим, что мы давим на тело, тогда мы нарушаем равновесие между атомами, приближая их друг к другу. Атомы, в свою очередь, не очень хотят куда-то уходить со своих родных мест, из-за чего возникают силы отталкивания. Здесь кристаллическая решетка тела схожа с пружинами, которые скрепляют атомы и не дают им сдвинуться с места. Сумма всех сил отталкивания между атомами в теле и создает общую силу упругости тела.
Упругость — свойство тела изменять свою форму и размеры при внешнем воздействии и восстанавливаться до исходного состояния при прекращении действия внешних сил.

Остановимся на частных случаях проявления силы упругости.
Мы помним, что каждое тело давит на опору своим весом \(\overrightarrow{P}\). При этом возникает обратная сила, действующая на тело со стороны опоры, на которой находится это тело (по третьему закону Ньютона). Эта сила называется силой реакции опоры.
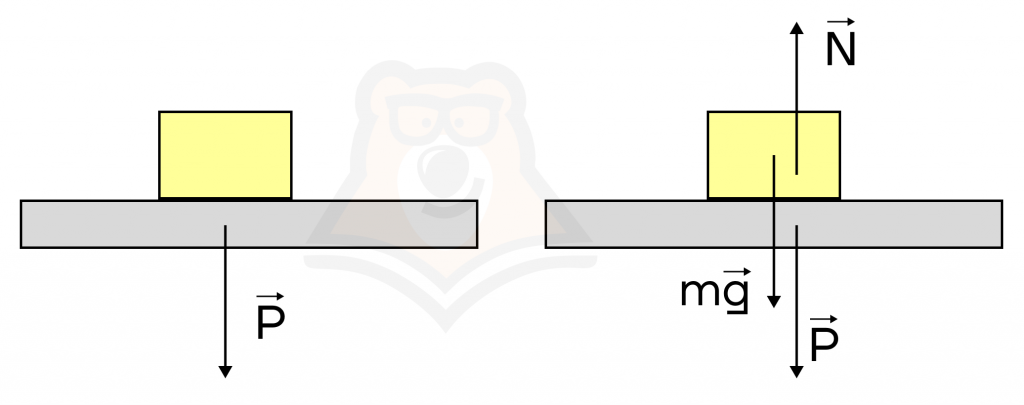
Сила реакции опоры — сила упругости, приложенная к телу со стороны опоры и действующая перпендикулярно поверхности.
То есть на изображении выше тело давит на опору весом \(P\), тогда опора создает такую же силу, которая препятствует внешнему воздействию. Это и есть сила реакции опоры \(\overrightarrow{N}=-\overrightarrow{P}⇔ |\overrightarrow{N}|=|\overrightarrow{P}|\), что подтверждается третьим законом Ньютона (сила действия равна силе противодействия).
Вторым частным случаем проявления силы упругости является сила натяжения.
Сила натяжения — сила, действующая на тело со стороны пружины или подвеса.
Например, вагонетка прикреплена к стене с помощью пружины. Если мы потянем за вагонетку, то пружина деформируется и создаст силу, препятствующую ее деформации. Как и в предыдущем случае, эта сила направлена против внешнего воздействия, и чем большую силу мы приложим, тем сложнее будет тянуть вагонетку и растягивать пружину. То есть сила натяжения возрастает при увеличении деформации пружины.
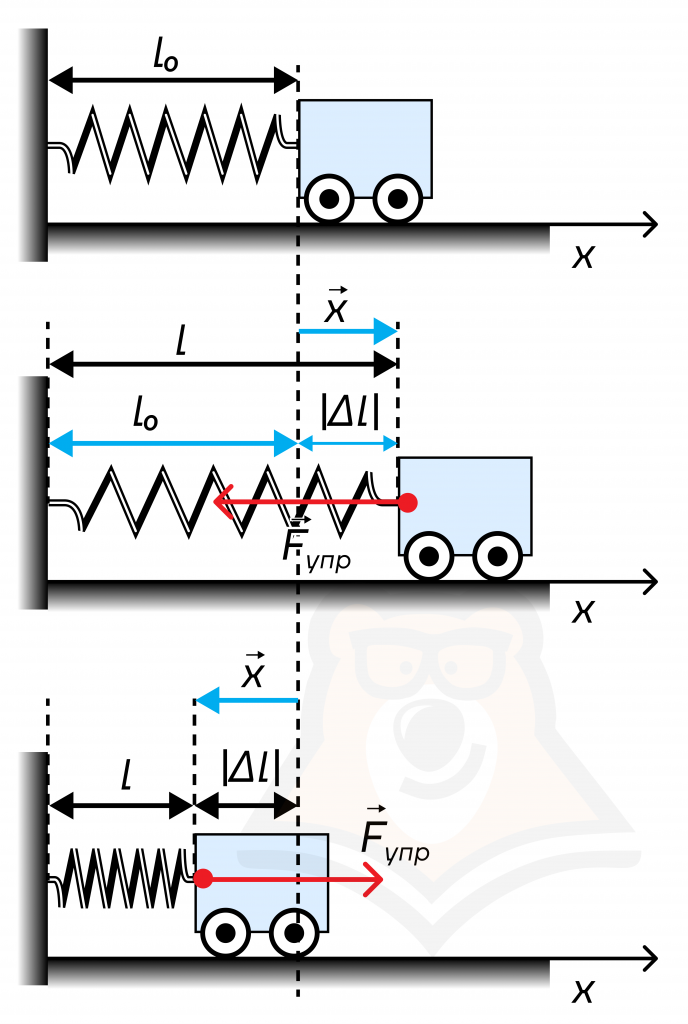
Здесь деформация выражается формулой \(|\Delta x|=|l-l_0|\). Знак модуля показывает, что изменение длины мы всегда считаем положительным.

Забираем с собой весь багаж полученных знаний и «плывем» дальше.
Закон Гука и сила упругости пружины
Для нахождения силы упругости, которая возникает при деформации пружины или другого упругого дела, английский физик Роберт Гук вывел закон.
Закон Гука: Модуль силы упругости \(F_{упр}\overrightarrow{}\), возникающей при деформации пружины, пропорционален удлинению этой пружины \(\Delta x\).
| \(F_{упр}=-k\Delta x\), где \(Fупр\) — сила упругости (Н); \(k\) — жесткость пружины (Н/м); \(\Delta x\) — удлинение пружины. |
Минус в формуле имеет физический смысл.
- Если \(\Delta x=l-l_0>0\), т.е. тело растянуто, то \(F<0\), т.е. сила упругости стремится сжать тело к исходному состоянию.
- Если \(\Delta x=l-l_0<0\), т.е. тело сжато, то \(F>0\), т.е. сила упругости стремится растянуть тело в исходное состояние.
Остановимся поподробнее на параметре \(k\).
Жесткость
Жесткостью называют такую физическую величину, которая характеризует способность пружины или другого упругого тела не подвергаться деформации под действием внешней силы.
Приведем пример. Возьмем обычную резинку для волос и повесим ее на крючок. Начнем навешивать на нее одинаковые бусины по одной штуке, резинка при этом начнет растягиваться. Если резинка упругая, то ее растяжение будет маленьким, а если «слабенькая» и не упругая, то растягиваться она будет гораздо сильнее.
Вот эта способность «не растягиваться» характеризуется коэффициентом жесткости k.
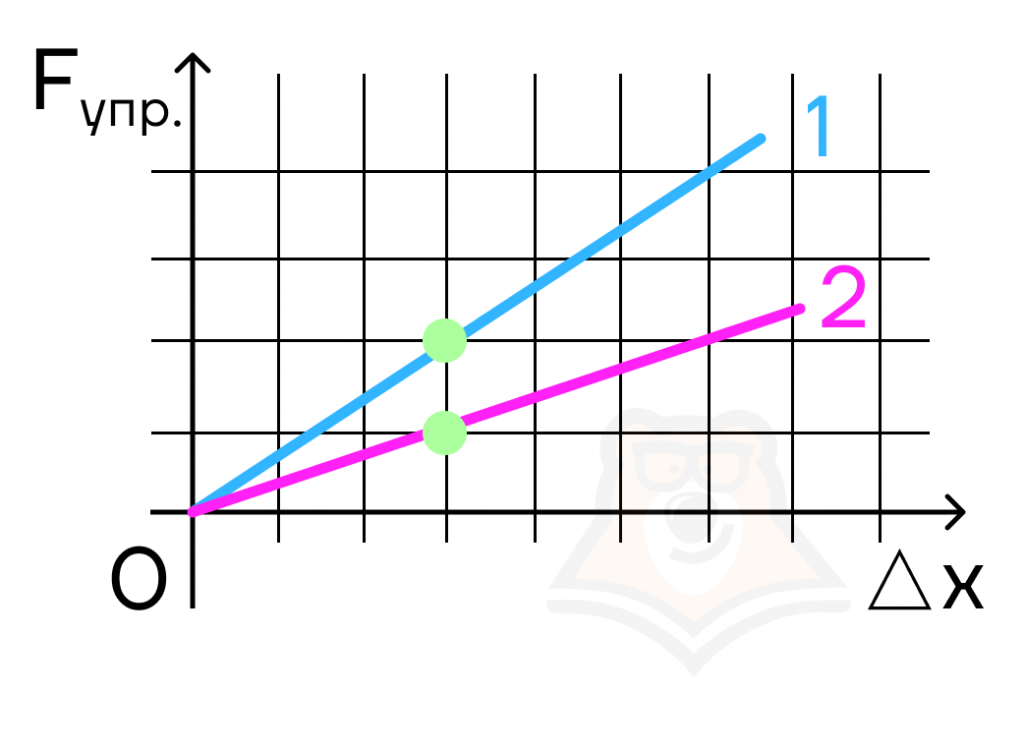
Чем сильнее деформация резинки \(\Delta x\) под весом бусин, тем больше будет значение силы упругости. При желании даже можно построить график зависимости силы упругости, возникающей в резинке, от деформации \(\Delta x\) для резинки №1 (упругой) и №2 (неупругой).
В чем же будет разница? Отметим на этом графике 2 точки, для которых \(\Delta x\) будет одинаковой. Мы видим, что \(F_{упр1}> F_{упр2}\). Так как деформация у них одинаковая, то силы упругости могут отличаться только из-за \(k: k_1 > k_2\). Это значит, что, чтобы добиться одинаковой деформации, к 1 резинке надо приложить большую силу, то есть подвесить больше бусин, чем ко 2.
На графике это характеризуется углом наклона к горизонтальной оси: чем больше угол наклона, тем больше k.
Физический смысл параметра k – тангенс угла наклона прямой к оси абсцисс. То есть чем больше k, тем больше угол наклона прямой – он стремится к прямому углу, тем больше тангенс угла наклона.
Это самый простой случай. Давайте посмотрим, что будет, если у нас будет система из нескольких упругих тел.
Жесткость системы из нескольких пружин
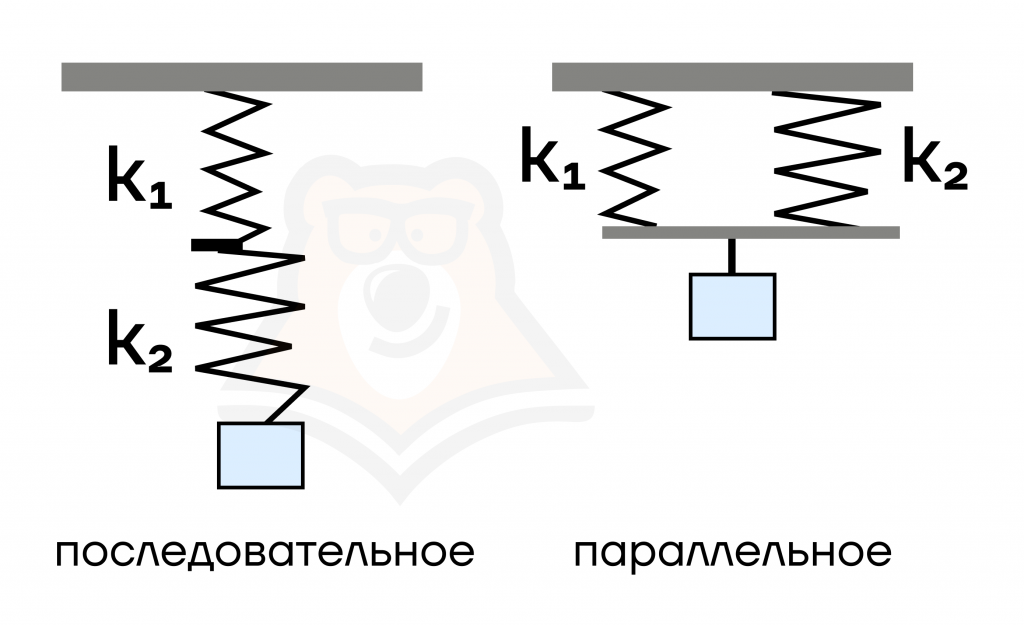
Существуют сложные системы из пружин. Их бывает всего 2 вида, которые представлены на изображении: последовательное и параллельное соединения.
Последовательное соединение пружин – соединение, при котором каждая новая пружина соединяется с предыдущей. При этом крайние пружины соединены с опорой и с грузом.
Параллельное соединение пружин – соединение, при котором все пружины соединены и с опорой, и с грузом одновременно.
В таких случаях удобнее приводить задачу к подобной, где мы заменяем несколько пружин одной с новым коэффициентом жесткости, который равен общей жесткости изначальных пружин. Это тот случай, когда меньше лучше, чем больше, и не надо сомневаться.

- Для параллельного соединения: \(k_{общ}=k_1+k_2\), как сумма жесткостей всех пружин.
- Для последовательного соединения: \(\frac{1}{k_{общ}}=\frac{1}{k_1}+\frac{1}{k_2}\), как сумма обратных жесткостей пружин для расчета обратной жесткости системы.
Частным случаем силы упругости является сила натяжения нити. Для ее вычисления нет определенной формулы, она выводится из 2 закона Ньютона, как неизвестная сила. Сила натяжения нити всегда направлена вдоль нити и приложена к месту контакта тела с нитью. Пример приведен на картинке.
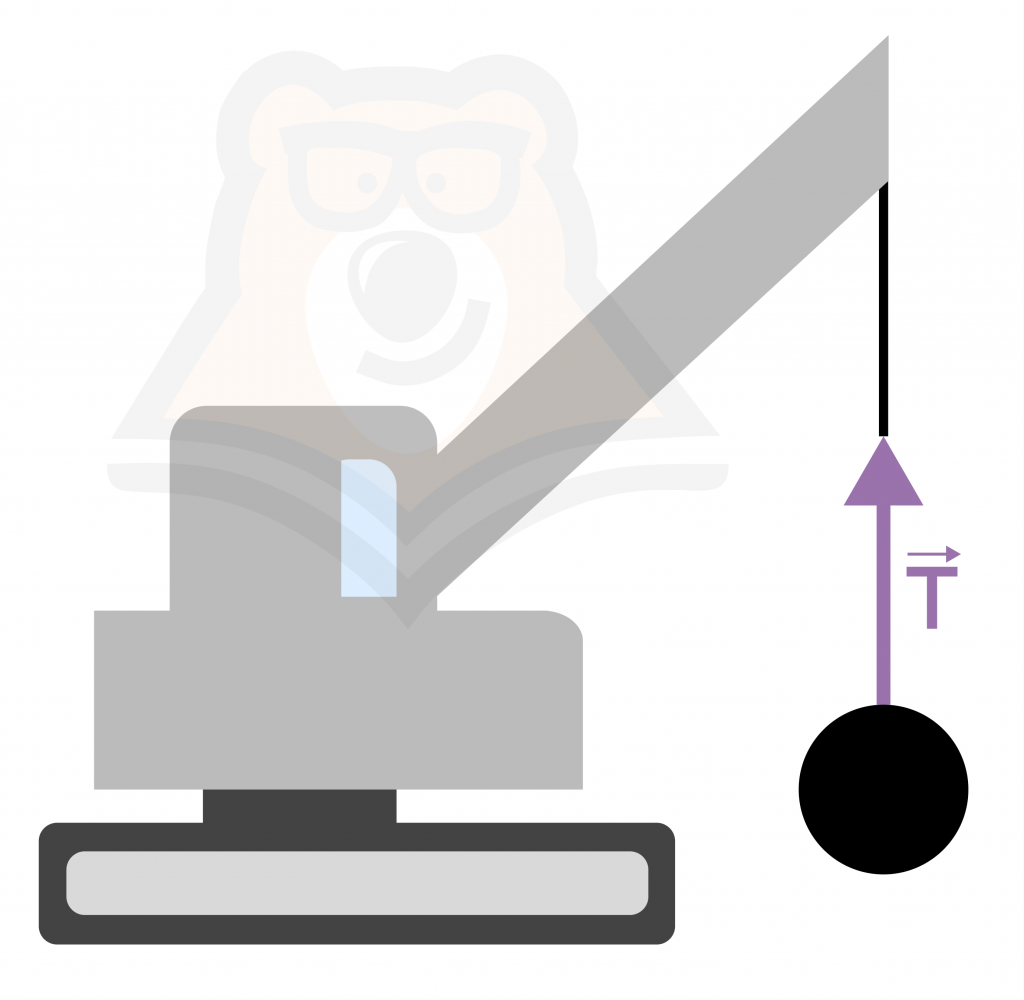
Возникает вполне логичный вопрос: но нить же тоже растягивается при воздействии на нее.
Ответ прост: если нить деформируется, то мы ее рассматриваем как пружину и пользуемся законом Гука. Поэтому в задачах часто используют термин «нерастяжимая нить», который говорит о том, что мы можем не учитывать в решении задачи Закон Гука для нити, и передача усилия от всех сил по 2 закону Ньютона переходит через нить без изменения — то есть нить не меняет ускорение системы тел. Это часто используют в обосновании к 30 заданию ЕГЭ по физике.
Давайте проверим теорию на практике. Такие задачи могут встретиться в номере 23 ЕГЭ.
Задание. При исследовании зависимости величины деформации пружины от приложенной силы ученику необходимо выбрать два набора. Запишите их номера.
| Номер набора | Материал пружины | Масса одного груза, г | Количество грузов |
| 1 | Сталь | 350 | 2 |
| 2 | Медь | 200 | 4 |
| 3 | Сталь | 200 | 4 |
| 4 | Медь | 350 | 2 |
| 5 | Медь | 350 | 4 |
Решение. В практических заданиях такого рода важно для себя определить, какой параметр от чего зависит. В данном случае речь идет о деформации: \(\Delta x=l-l_0\). Пружина деформируется под действием внешней силы, в данном случае речь идет о силе тяжести грузиков, которые вешаются на пружину и растягивают ее. Сила тяжести находится по формуле \(F = mg\), то есть зависит только от массы грузов. Значит, надо выбрать два набора, в которых будет отличаться только количество грузов, а все остальные параметры будут идентичными, чтобы исключить их влияние на результат. Под это подходят набор 4 и 5. Материал пружин одинаковый, масса одного груза то же, а количество отличается в 2 раза.
Ответ: 45
Но сила упругости не единственная сила, обусловленная электромагнитным взаимодействием атомов веществ друг с другом. Самое время перейти к следующему разделу.
Сила трения
По секрету, с этой силой мы сталкиваемся с рождения, когда начинаем задевать предметы вокруг себя, ползать, делаем первые шаги, разбрасываем игрушки и т.д. Но обо всем по порядку.
Сила трения — сила, возникающая при соприкосновении поверхностей тел, которая препятствует их движению относительно друг друга и направлена вдоль линии их соприкосновения противоположно движению.
Это происходит, потому что поверхности соприкасающихся тел при рассмотрении под микроскопом имеют неровности, которые как бы «цепляются» друг за друга. Они по размеру сопоставимы с размером нескольких атомов, поэтому, когда две поверхности соприкасаются, между атомами двух тел возникают силы притяжения, которые мешают взаимному перемещению этих тел.
| Как первый номер стал «осиновым колышком» на ЕГЭ 2022? На ЕГЭ 2022 в некоторых КИМ был вопрос о природе сил трения. Многие ученики ответили, что сила трения обладает гравитационной природой, однако это не так. Стоит запомнить, что сила трения и сила упругости обладают электромагнитной природой из-за того, что эти силы возникают в результате существования сил взаимного притяжения и отталкивания между атомами. |

Без действия этой силы мы бы не смогли стоять на месте и ходить в принципе: мы бы постоянно скользили по поверхности без возможности повлиять на этот процесс.
На самом деле в природе существует несколько видов трения. На иллюстрации ниже можно подробнее узнать, какие именно.
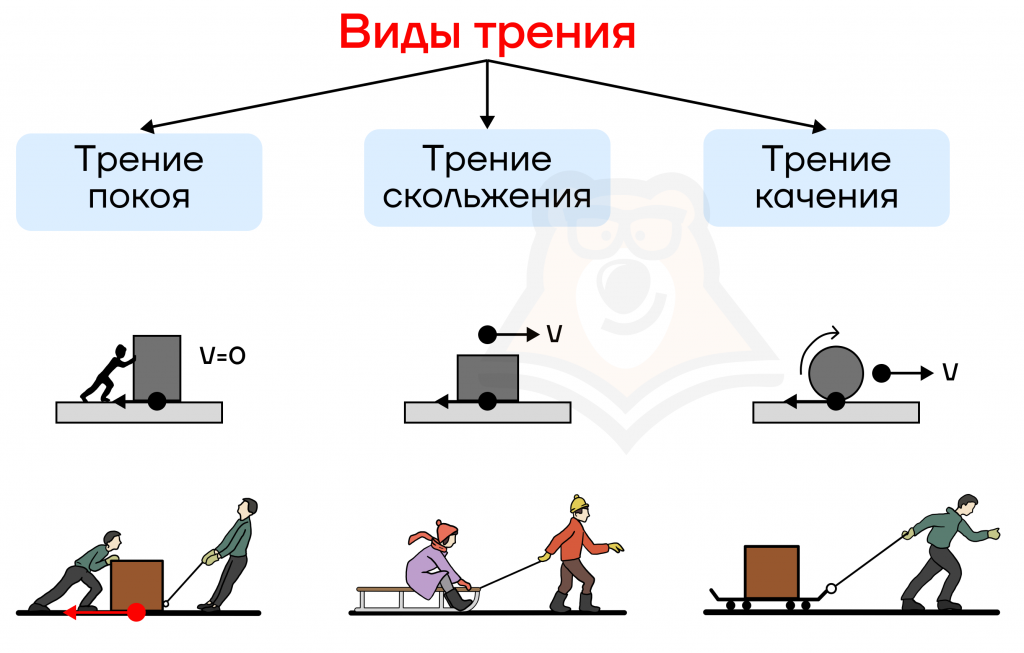
Рассмотрим каждый из видов силы трения.
Трение покоя — трение, возникающее при отсутствии относительного движения поверхностей.
Благодаря этой силе, тела и удерживаются на месте. На изображении выше люди пытаются сдвинуть шкаф. Пока шкаф покоится, на него действует сила трения покоя.

Начнем прикладывать к шкафу силу \(\overrightarrow{F}\), сначала маленькую, потом чуть побольше. Несмотря на то что мы увеличиваем силу, шкаф все еще продолжает покоиться, потому что все время этой силе препятствует сила трения покоя \(F_{тр.пок}\overrightarrow{}=\overrightarrow{F}\), которая увеличивается по модулю вместе с силой \(\overrightarrow{F}\). То есть сила трения покоя может принимать значения от 0 (когда тело покоится и на него не действуют никакие силы) до какого-то максимального значения, при котором ее станет недостаточно, и шкаф начнет двигаться под действием силы \(\overrightarrow{F}\). Условно эту зависимость можно показать в виде графика зависимости \(F_{тр.пок}\overrightarrow{}\) от \(F\overrightarrow{}\).
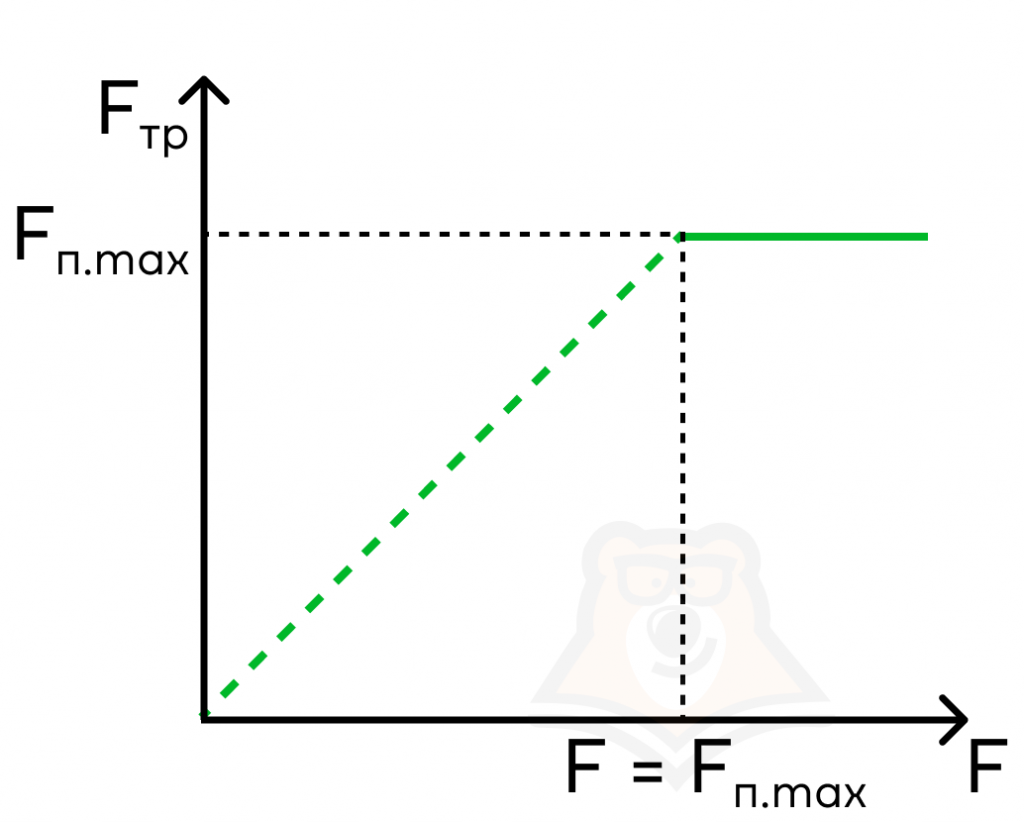
Как мы уже сказали, у этой силы есть свой предел, после преодоления которого тело начнет свое движение, то есть \(F_{тр.пок}\) станет равна \(F_{max}\) и перестанет расти по модулю. Эту силу называют силой трения скольжения \(F_{тр.ск}\).
Трение скольжения — трение, возникающее при относительном движении поверхностей двух соприкасающихся тел.
Формула силы трения скольжения выглядит так:
| \(F_{тр.ск}\overrightarrow{}=μ\overrightarrow{N}\), где \(F_{тр.ск}\) — сила трения скольжения (Н); \(μ\) — коэффициент трения (всегда меньше 1); \(N\) — сила реакции опоры (Н). |
И сразу же применим эту формулу для решения задачи. Такие задания могут встретиться в номере 2 ЕГЭ.
Задание. На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 25 Н. Чему будет равна сила трения скольжения, если коэффициент трения уменьшится в 5 раз при неизменной массе? (Ответ дайте в ньютонах).
Решение. Для более наглядного решения сделаем схему со всеми силами, действующими на тело.
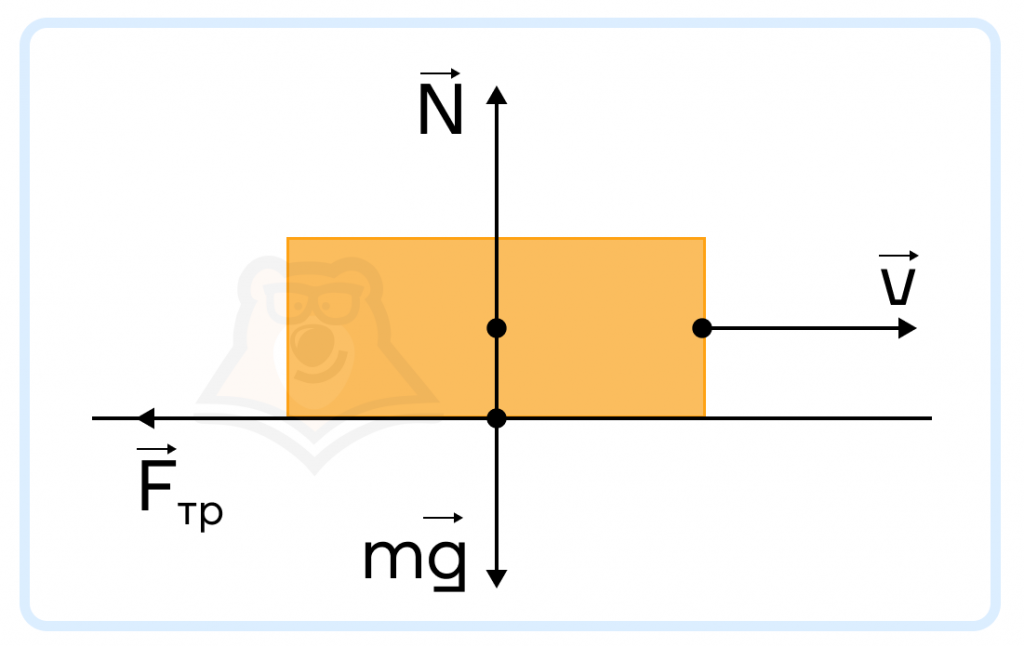
Сила трения скольжения находится по формуле \(F_{тр.ск}=μN\). Так как на брусок в вертикальном направлении действуют только сила тяжести и сила реакции опоры, по второму закону Ньютона \(N=mg\). Значит, \(F_{тр.ск} = μmg\). Если масса бруска не изменится, то после уменьшения коэффициента трения в 5 раз, сила трения скольжения также уменьшится в 5 раз и окажется равной:
\(F_{тр.ск.2}=\frac{F_{тр.ск.1}}{5}=\frac{25Н}{5}=5Н\).
Ответ: 5
Из формулы силы трения видно, что она зависит только от двух величин:
- коэффициента трения – он зависит от шершавости поверхности, чем она больше, тем выше будет \(μ\);
- силы реакции опоры – про нее очень подробно описано в статье «Сила тяготения. Сила тяжести и вес».
В большинстве случаев \(N=mg\), т.е. сила реакции опоры зависит от массы груза. Это позволяет нам провести мысленный эксперимент и представить, что будет с телом, если мы постепенно будем увеличивать его массу.
Например, возьмем санки и младших братьев и сестер и будем везти их по снегу. Сначала санки едут пустыми, везти их довольно просто, потом на санки садится первый ребенок, становится чуть тяжелее, потом второй – еще тяжелее и так далее.
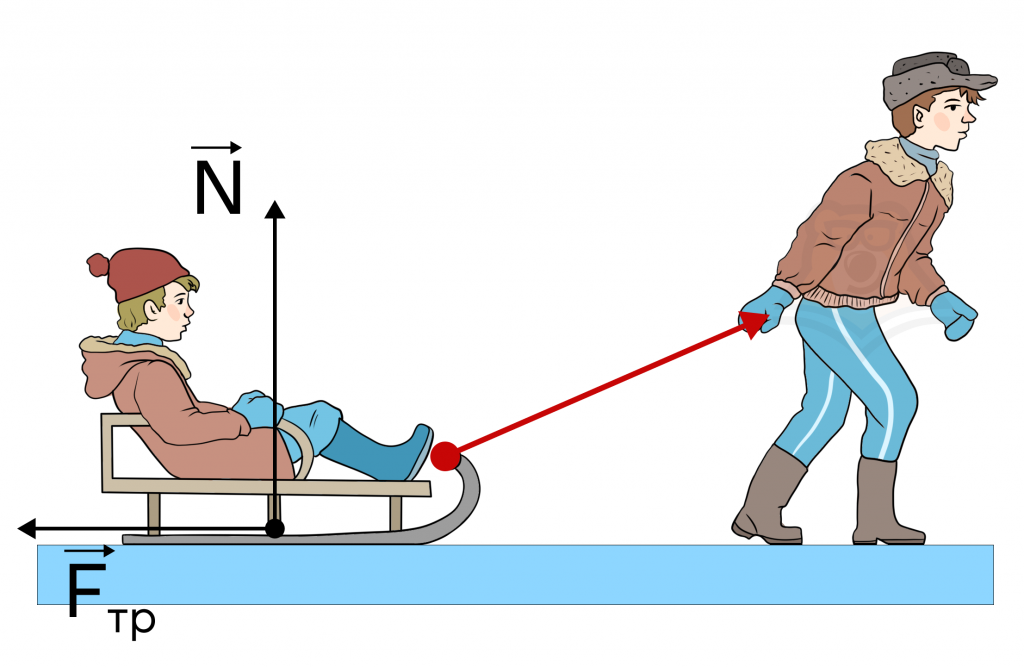
В этом примере увеличивается масса системы «санки – младшие братья-сестры», поэтому увеличивается \(N\), а значит, увеличивается и \(F_{тр.ск}\).
Эту зависимость \(F_{тр.ск}\) от \(N\) можно представить в виде графика наклонной прямой, где при увеличении \(N\) (отмечено на оси абсцисс) линейно увеличивается \(F_{тр.ск}\) (отмечено на оси ординат).
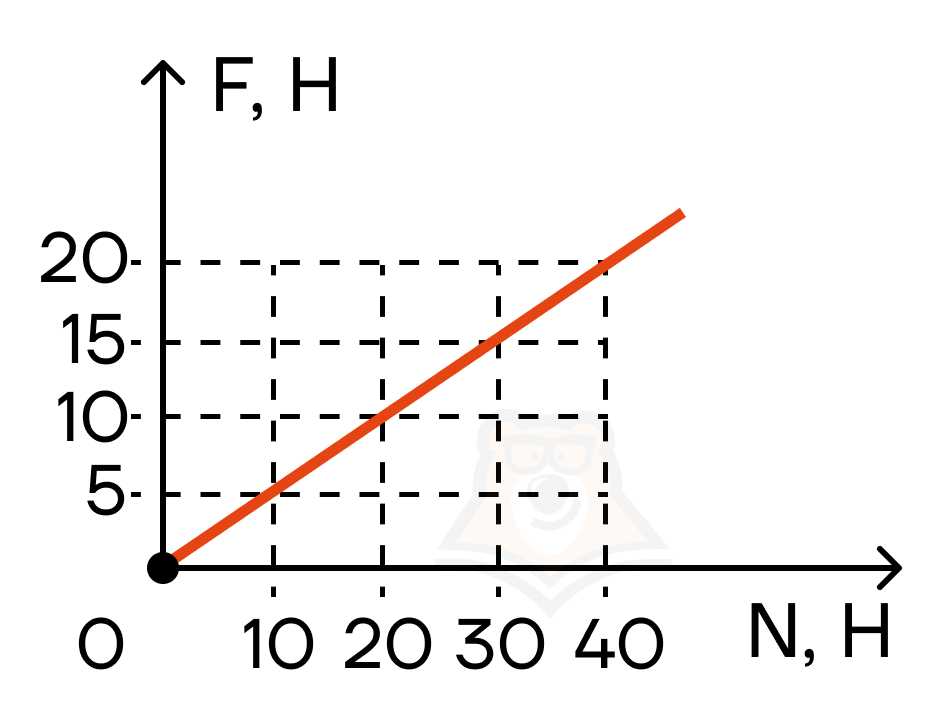
При этом в формуле силы трения скольжения нет параметра, который каким-либо образом зависел бы от площади соприкасающихся поверхностей. Поэтому очень важно запомнить, что сила трения скольжения не зависит от площади соприкосновения тела с поверхностью, а зависит только от силы реакции опоры и степени шершавости этих поверхностей.
При вращении тела по поверхности возникает сила трения качения.
Стоит отметить, что сила трения качения в разы меньше силы трения скольжения. И правда, катить шкаф на колесиках намного проще, чем толкать его по поверхности. Это происходит из-за того, что при скольжении на месте разрыва связей между атомами сразу возникают новые, а при качении скорость разрыва этих же связей происходит намного быстрее, чем их восстановление.
Основное отличие силы трения качения от силы трения скольжения в площади соприкасающихся поверхностей. Во время качения площадь соприкосновения все время меняется – колесо катится по дороге и все время соприкасается с ней новым участком. Это пример, когда возникает сила трения качения. Если то же самое колесо положить на землю и начать толкать его, везя по земле, в этом случае площадь соприкасающихся поверхностей не меняется, поэтому на колесо действует сила трения скольжения.
| Почему сила трения нам не враг? Нам часто казалось, что сила трения является нашим противником. Именно она не позволяет создать бесконечный двигатель. Однако без силы трения мы не смогли бы ходить, так как при шаге мы бы просто скользили. Мы бы не смогли создавать предметы, потому что инструменты не задерживались бы в наших руках. Без силы трения мир был бы совсем другим. |

Все силы в природе выполняют важную функцию, и у каждой своя роль.
Сила упругости препятствует деформации, помогает телам сохранять свою форму и размеры. Сила трения обеспечивает взаимодействие между телами, сцепку между деталями в механизмах, благодаря ей мы можем согреть ладони в холодный день, потерев их друг об друга, или ластиком стереть ошибку из тетради. Но кроме этих сил, существуют еще и другие, например, силы, действующие со стороны жидкостей на погруженные в них тела. Об этом подробнее можно узнать из статьи «Сила Архимеда. Давление».
Термины
Атом – мельчайшая частица вещества, сохраняющая все его химические свойства. Из атомов состоят молекулы, а из молекул состоит вещество, т.е. все, что имеет массу. Атом можно поделить на нейтроны, протоны и электроны.
Второй закон Ньютона – один из трех основных законов динамики, описывающий связь силы, действующей на тело, с ускорением, которое оно получает вследствие действия этой силы. Описывается он формулой: \(F=ma\), где \(F\) – это сила или равнодействующая всех сил, действующих на тело, \(m\) – масса тела, \(а\) – ускорение.
Кристаллическая решетка – геометрическая модель строения твердого вещества, состоящая, как правило, из атомов, находящихся в вершинах воображаемого параллелепипеда, и связей между ними, представляющихся в виде ребер этого параллелепипеда.
Третий Закон Ньютона – один из трех основных законов динамики, который говорит о том, что силы, с которыми взаимодействуют два тела, равны по модулю, но направлены в противоположные стороны.
Фактчек
- Сила упругости имеет электромагнитную природу.
- Сила упругости возникает при деформации тела под внешним воздействием.
- Сила упругости всегда направлена против внешнего воздействия перпендикулярно поверхности.
- Сила упругости связана с деформацией пружины линейной зависимостью.
- Жесткость системы пружин вычисляется по формуле \(k_{общ}=k_1+k_2\) при последовательном соединении и по формуле \(\frac{1}{k_{общ}}=\frac{1}{k_1}+\frac{1}{k_2}\) для параллельного соединения.
- Сила трения возникает при соприкосновении поверхностей тел.
- Сила трения всегда направлена противоположно движению тела относительно поверхности.
- Сила трения скольжения зависит от силы реакции опоры, степени шероховатости поверхности и не зависит от площади соприкасающихся поверхностей.
Проверь себя
Задание 1.
Какие тела могут возвращаться из деформированного состояния в исходное?
- все твердые
- все жидкие
- упругие
- пластичные
Задание 2.
С чем можно сравнить связь атомов в кристаллической решетке?
- с прутьями
- с нитями
- с энергетическим полем
- с пружинами
Задание 3.
Куда направлена сила упругости пружины?
- в сторону внешнего воздействия
- в сторону, противоположную внешнему воздействию
- перпендикулярно внешним силам
- однозначно определить нельзя
Задание 4.
Когда возникает сила трения скольжения?
- при относительном движении поверхностей
- при отсутствии относительного движения поверхностей
- при любом воздействии на тело
- при деформации тела
Задание 5.
Какая сила трения меньшая по модулю?
- сила трения скольжения
- сила трения качения
- максимальная сила трения покоя
- нет однозначного ответа
Ответы: 1. — 3; 2. — 4; 3. — 2; 4. — 1; 5. — 2.


 к списку статей
к списку статей





