Сечения
На этой странице вы узнаете
- Как дракон с помощью сечений разрушал город?
- Чем вода похожа на сечение?
- Что общего у следа на снегу и следа в сечении?
Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра…
Сечения
Как дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.

Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях. Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
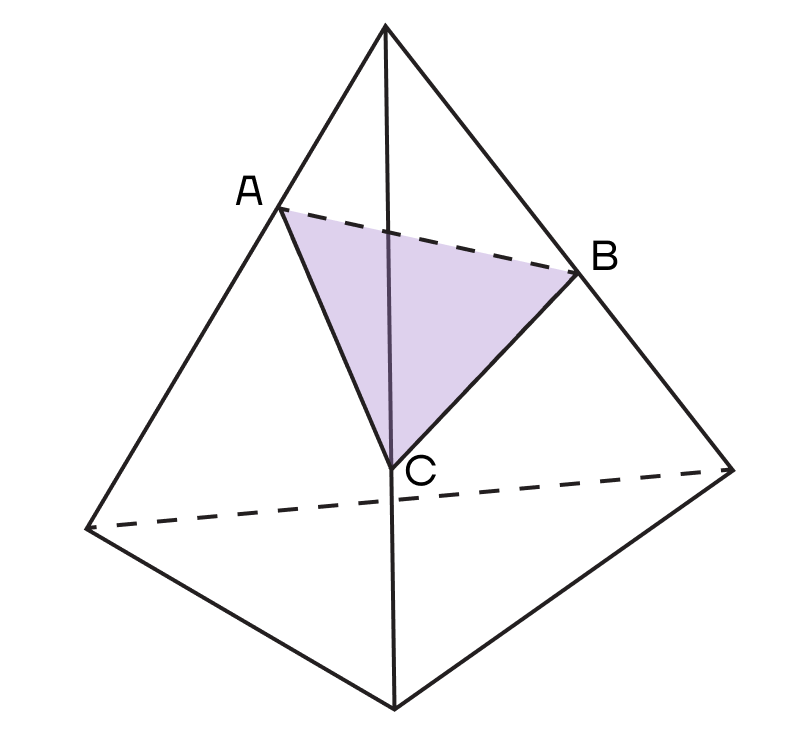
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение?
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.

А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.
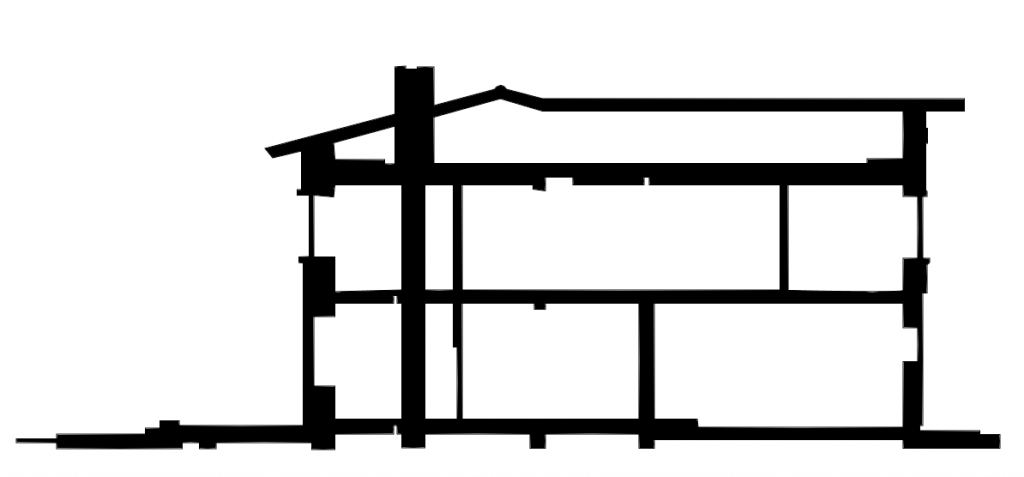
| Чем вода похожа на сечение? Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться. |

Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Методы построения сечений
Однако сечения нужно правильно построить. Для их построения существует несколько методов:
- Метод следов;
- Метод внутреннего проектирования;
- Комбинированный метод.
Разберем их по порядку.
Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева.

Все эти тела оставляют след на снегу.
| Что общего у следа на снегу и следа в сечении? Сечение так же, как и любое животное на снегу, оставляет след на гранях многогранника. И этот след — это сторона многоугольника, который образовывает сечение. |
Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы.
След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника.
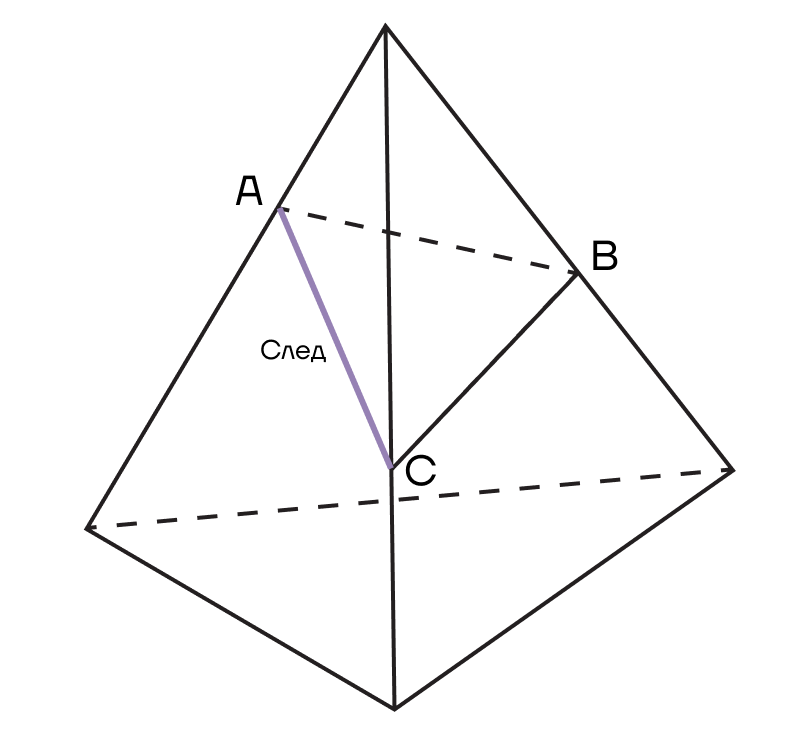
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно.
Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра.
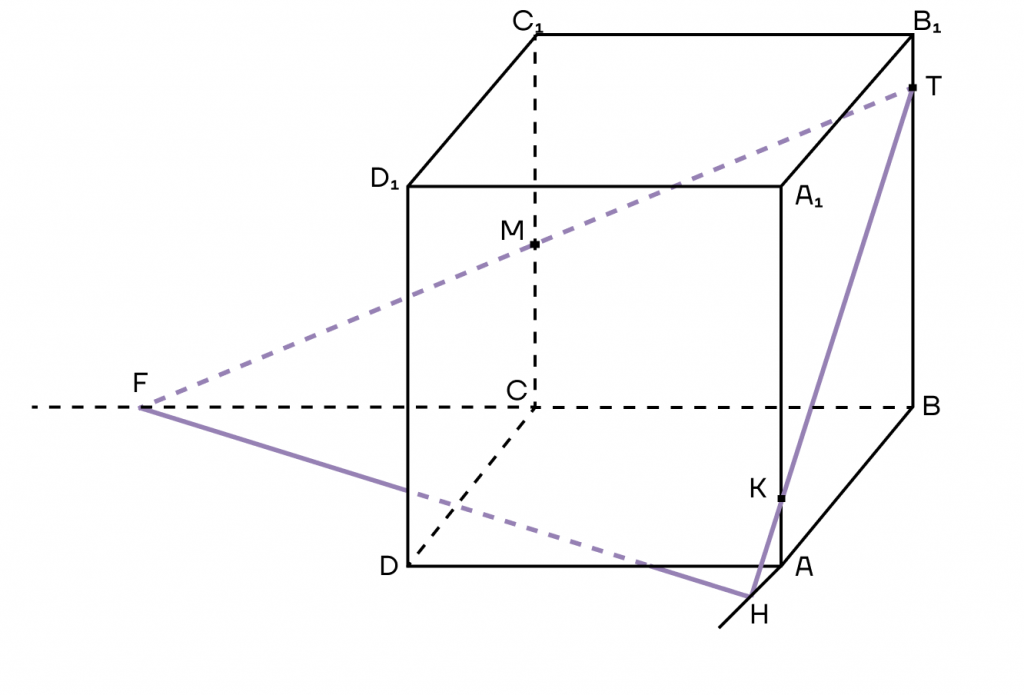
Построим сечение куба, которое проходит через точки К, М и Т, чтобы чуть подробнее разобраться в методе следов.
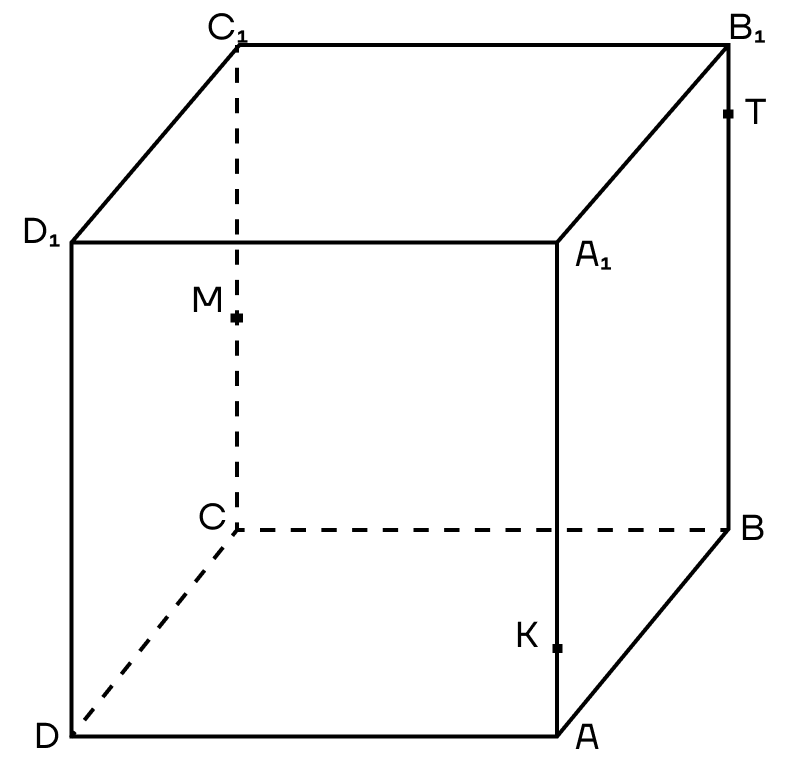
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить.
1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ1) и точки М и Т в плоскости (ВСС1). Поэтому мы можем их соединить.
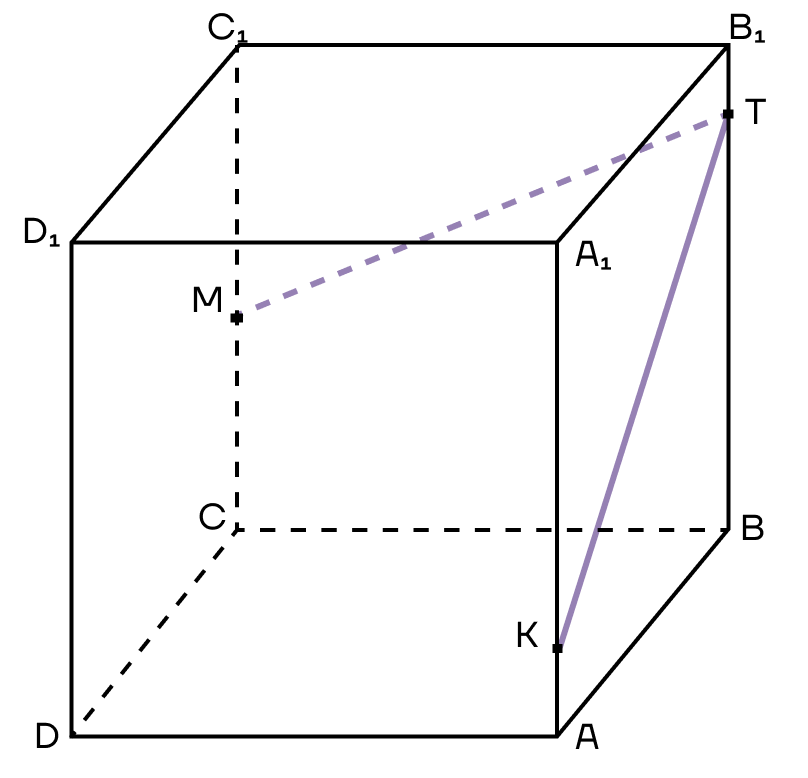
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами.
Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F.
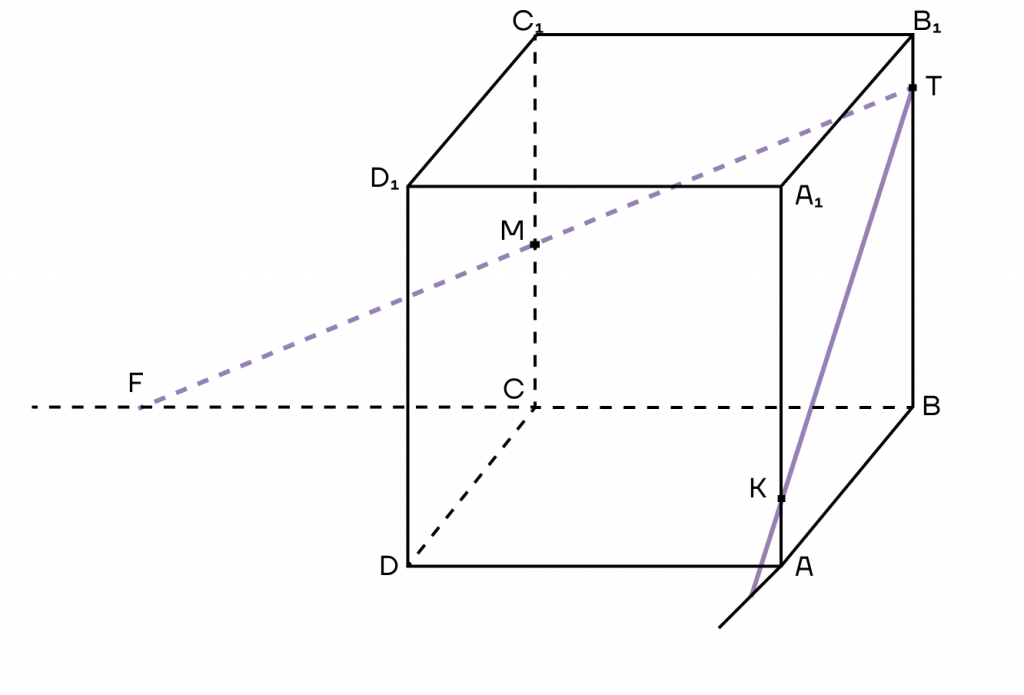
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб.
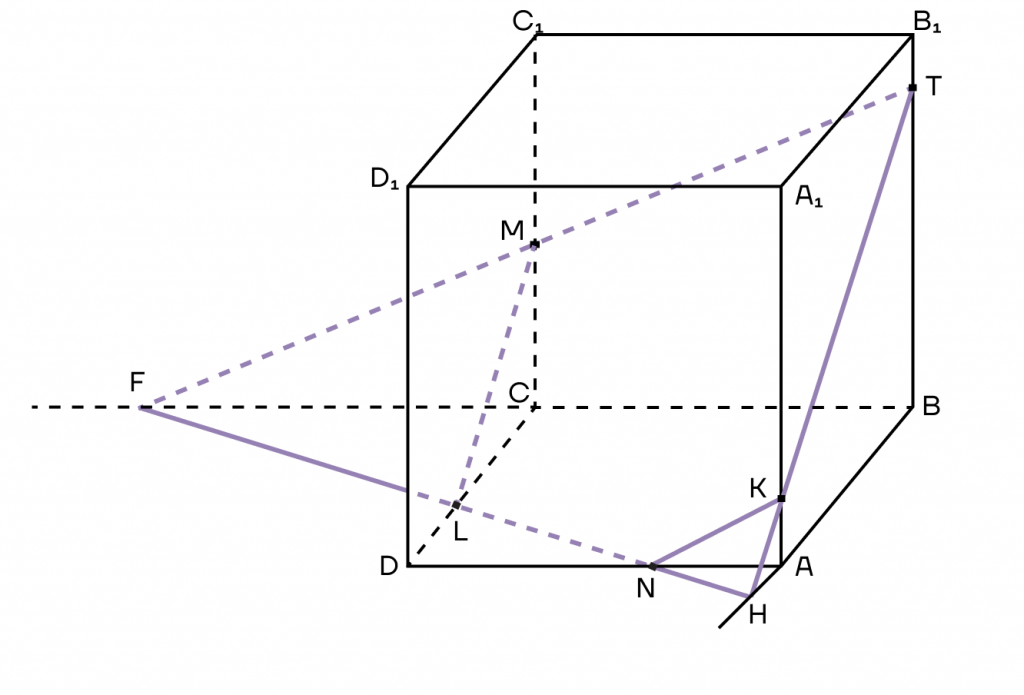
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.
5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L.
А также соединим все точки, которые окажутся в одной плоскости.
6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба.
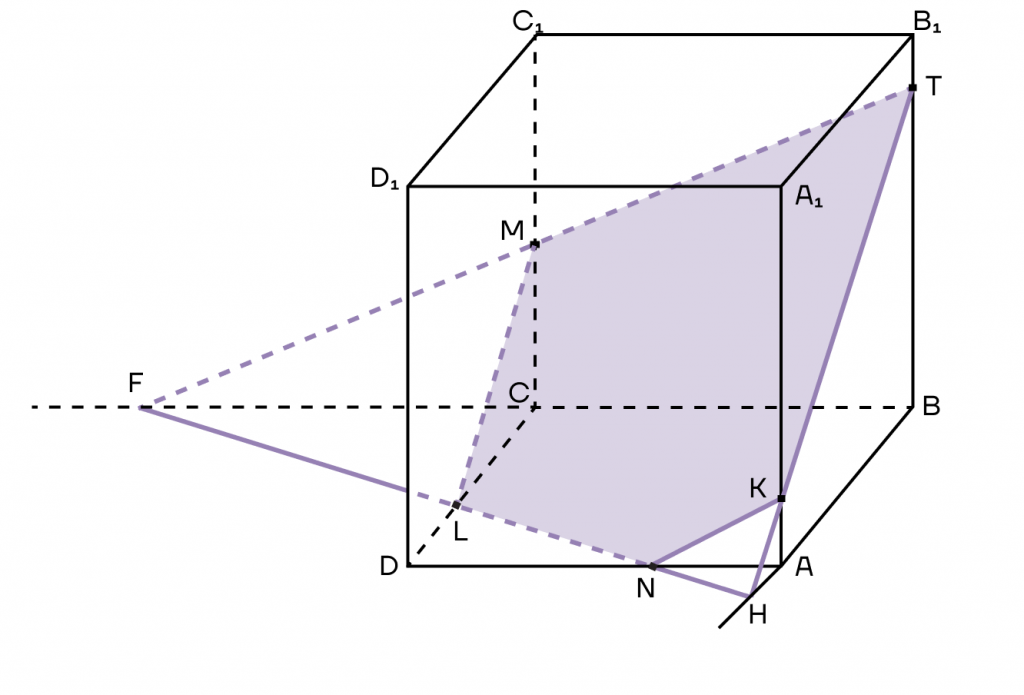
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер.
А также пользоваться лайфхаком: точки в одной плоскости можно соединять.
Рассмотрим метод внутреннего проектирования.
Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа.
В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т.
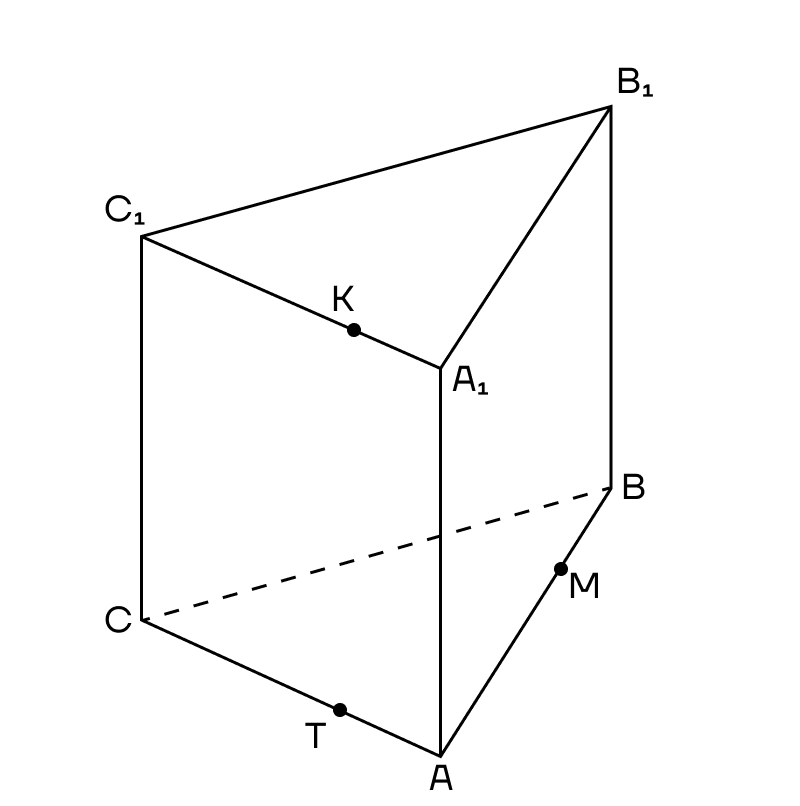
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1) и точки Т и М в плоскости (АВС).
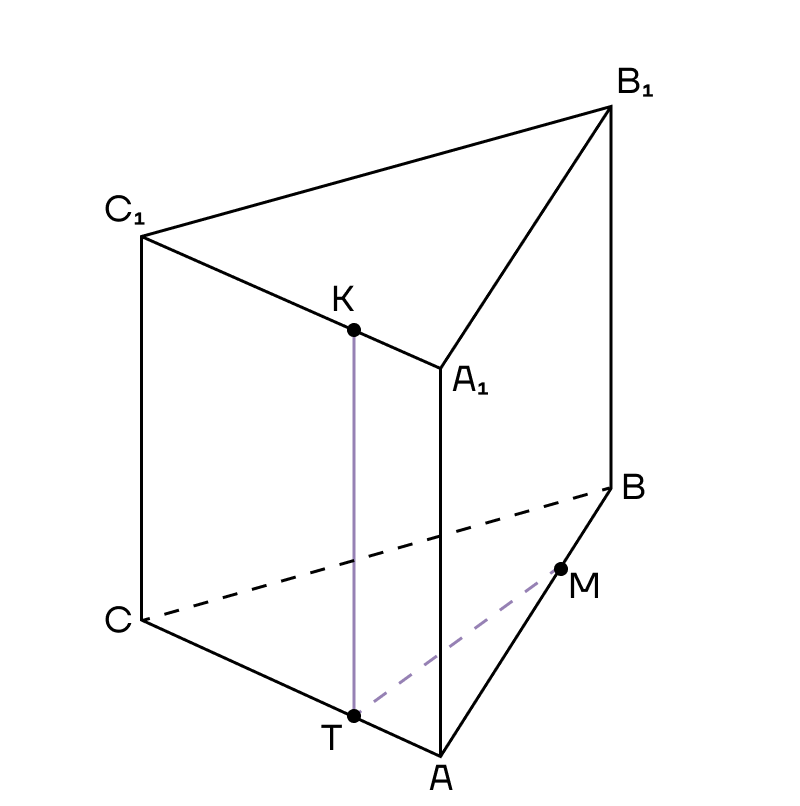
2. КТ проходит почти параллельно ребру АА1, следовательно, использовать метод следов не рационально.
3. Теперь посмотрим на плоскости (АВС) и (А1В1С1) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них.
В плоскости (АВС) лежит прямая ТМ, а в плоскости (А1В1С1) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.
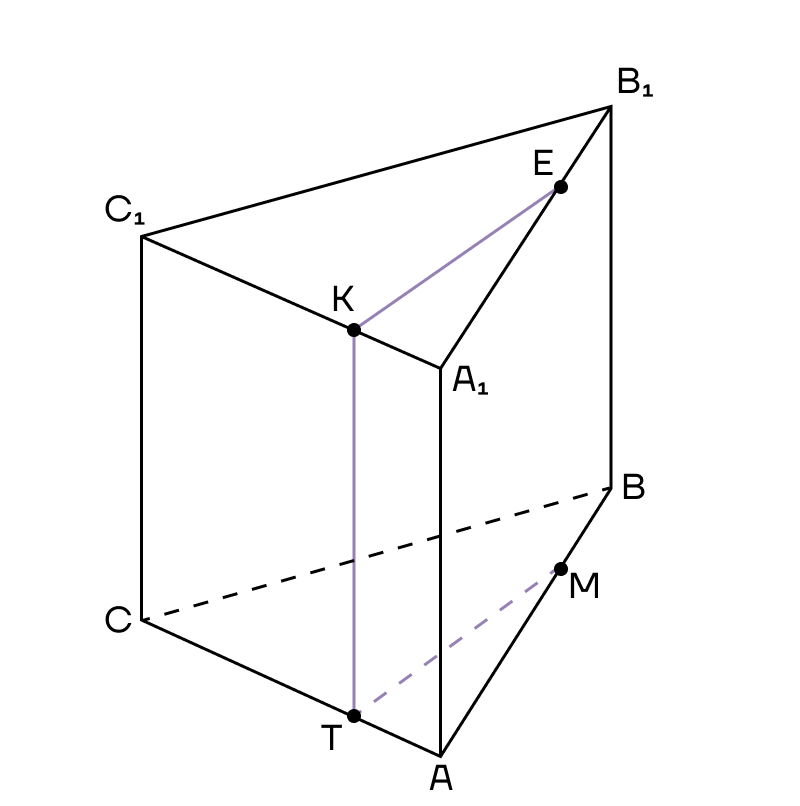
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы.
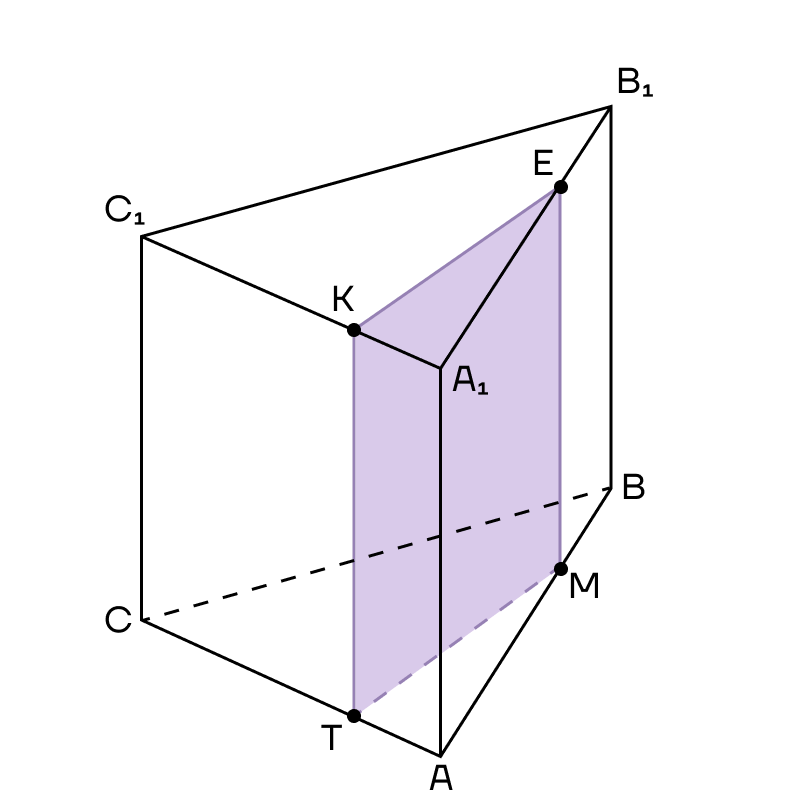
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.
Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования.
Примеры построения сечений
Рассмотрим несколько примеров построения сечений в различных фигурах.
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
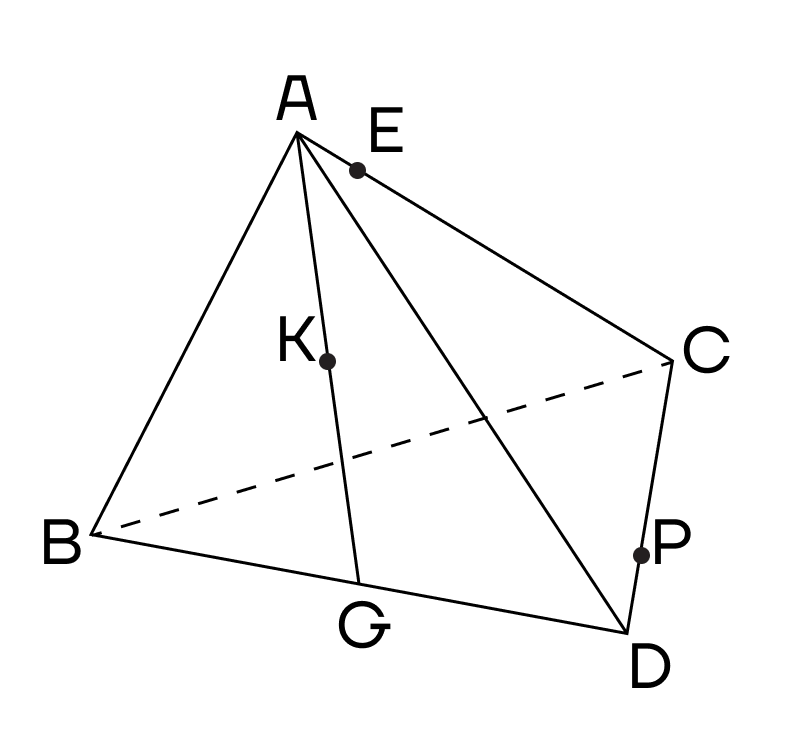
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
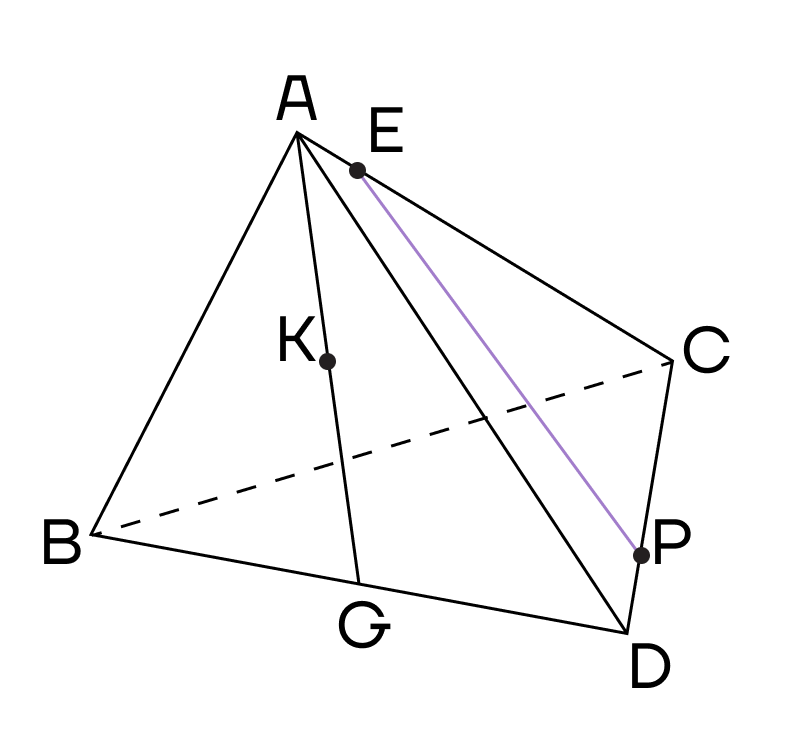
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
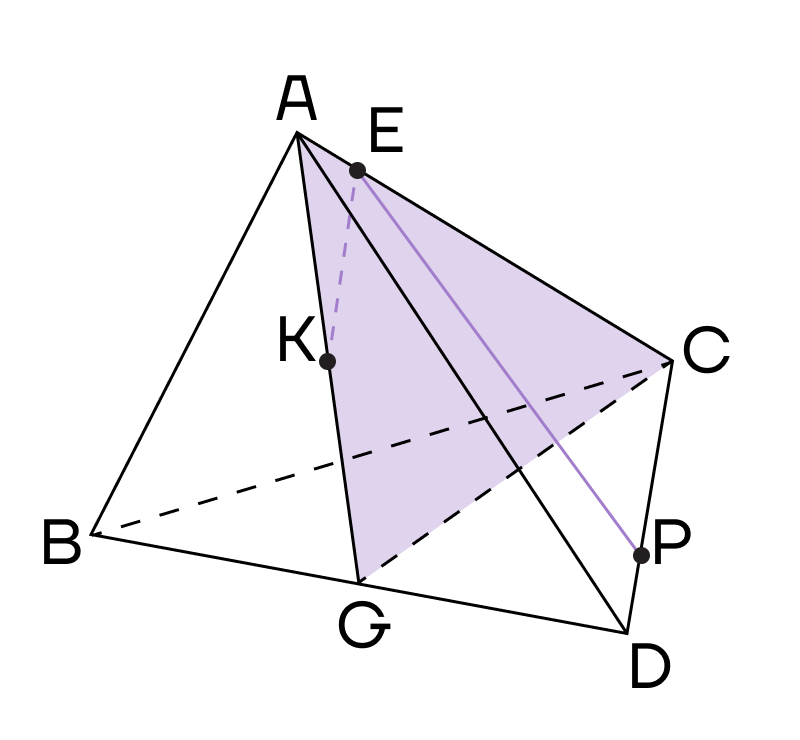
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
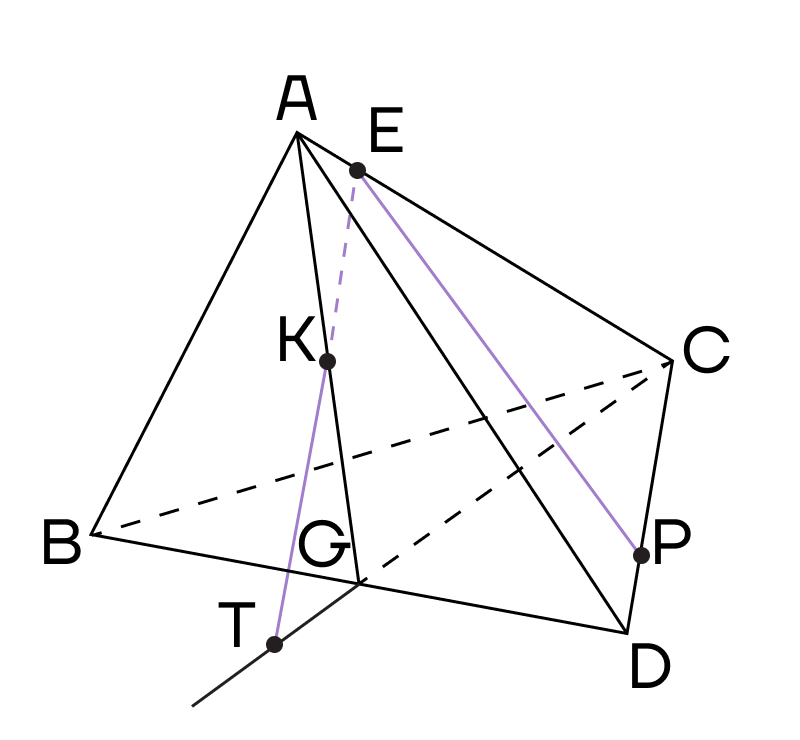
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
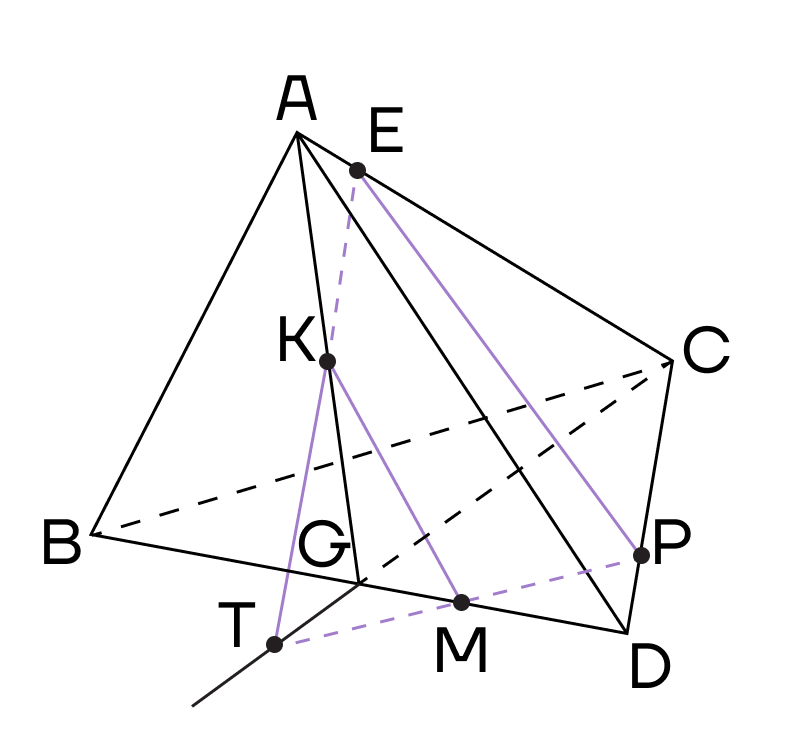
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
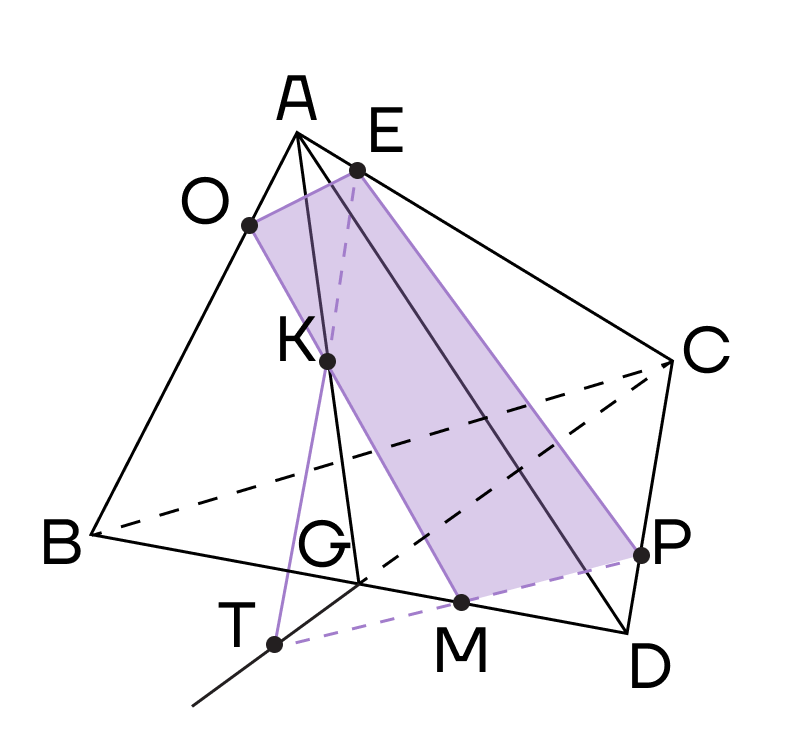
Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
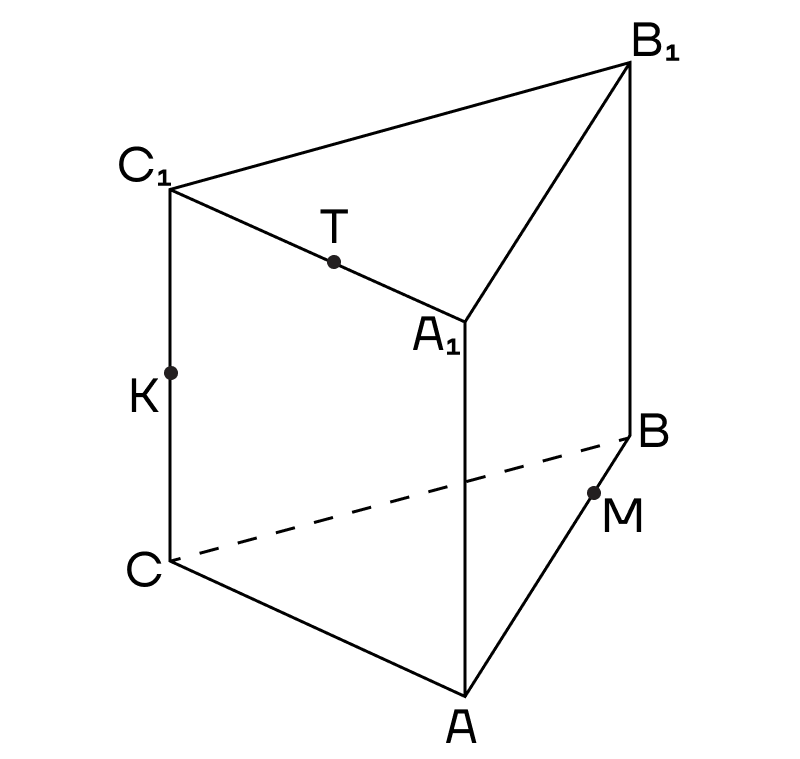
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
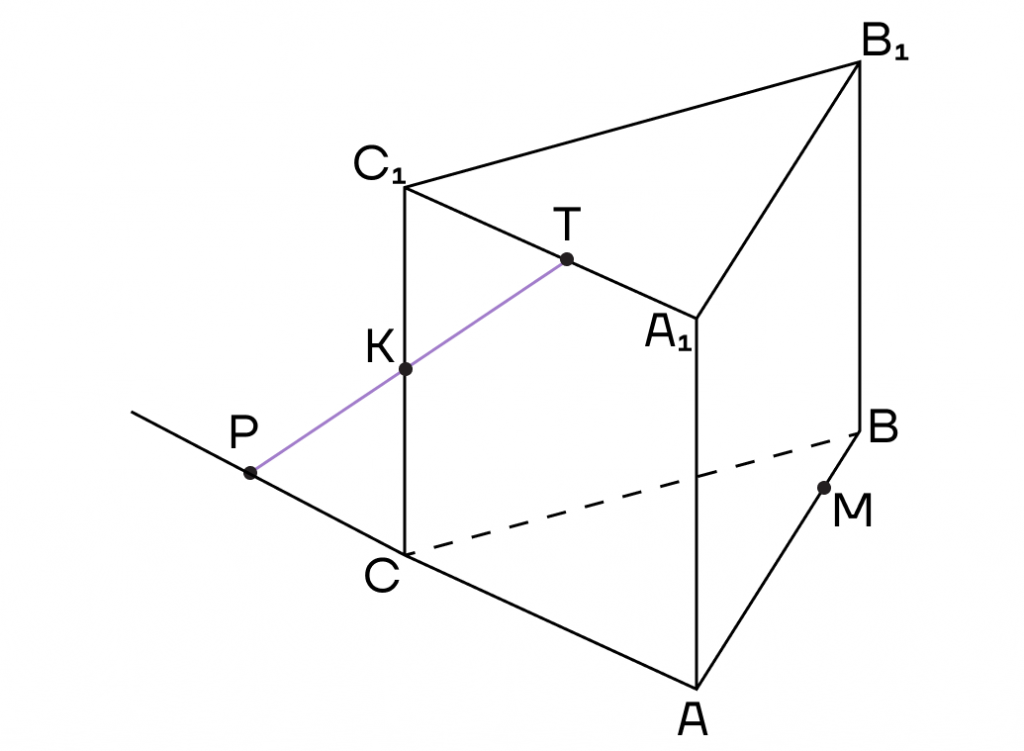
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
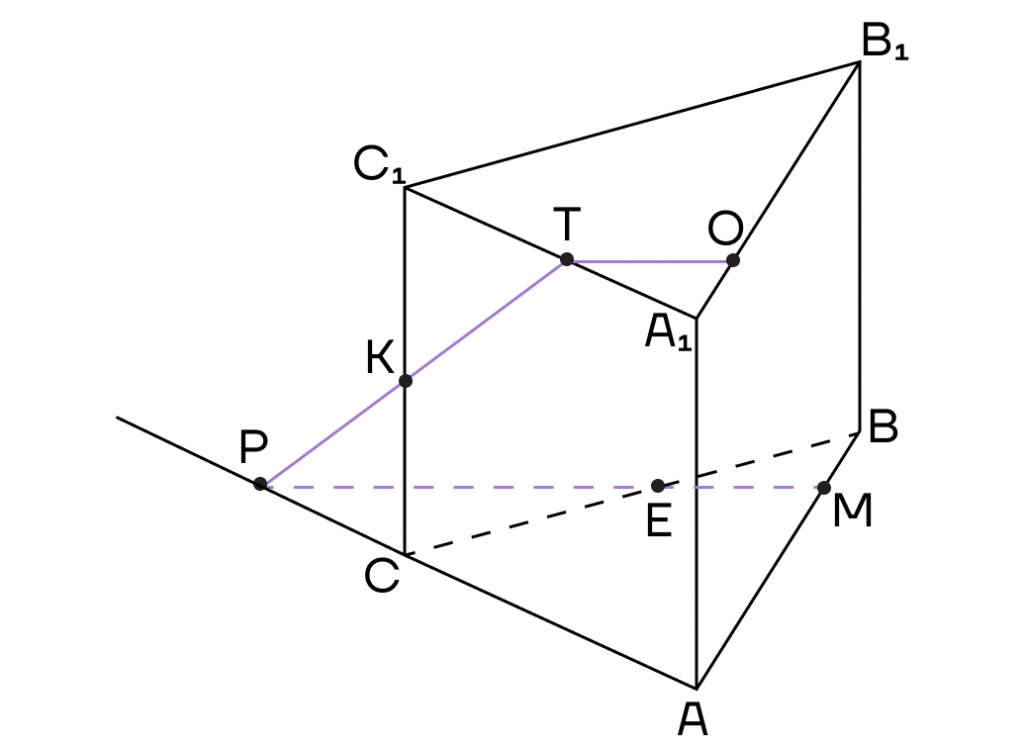
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
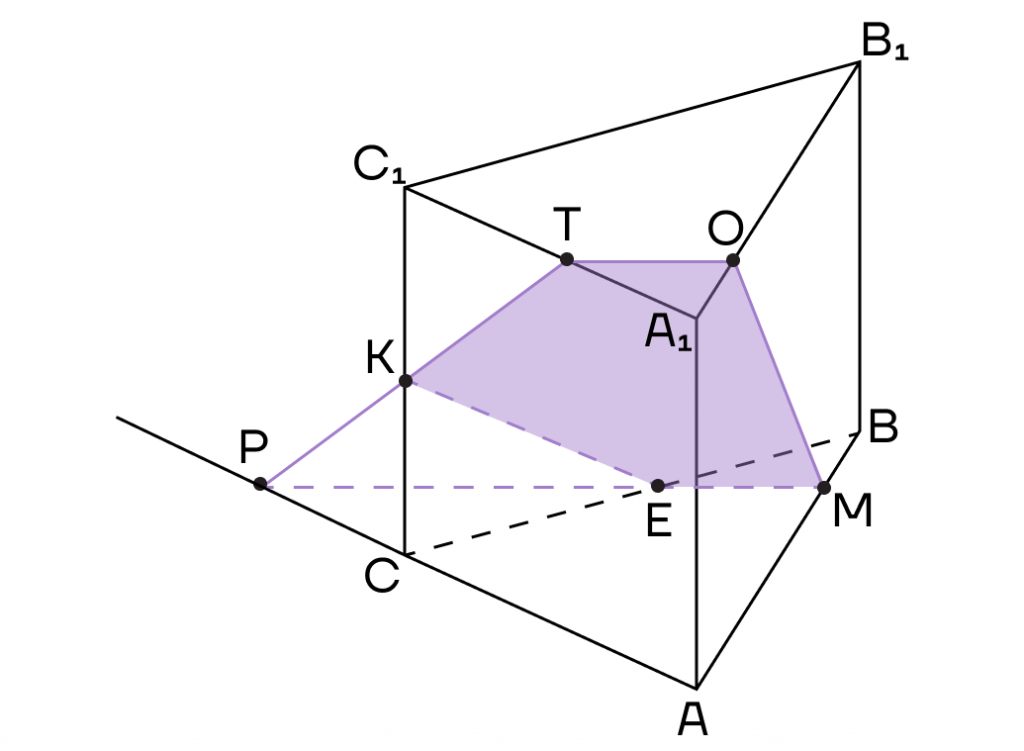
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
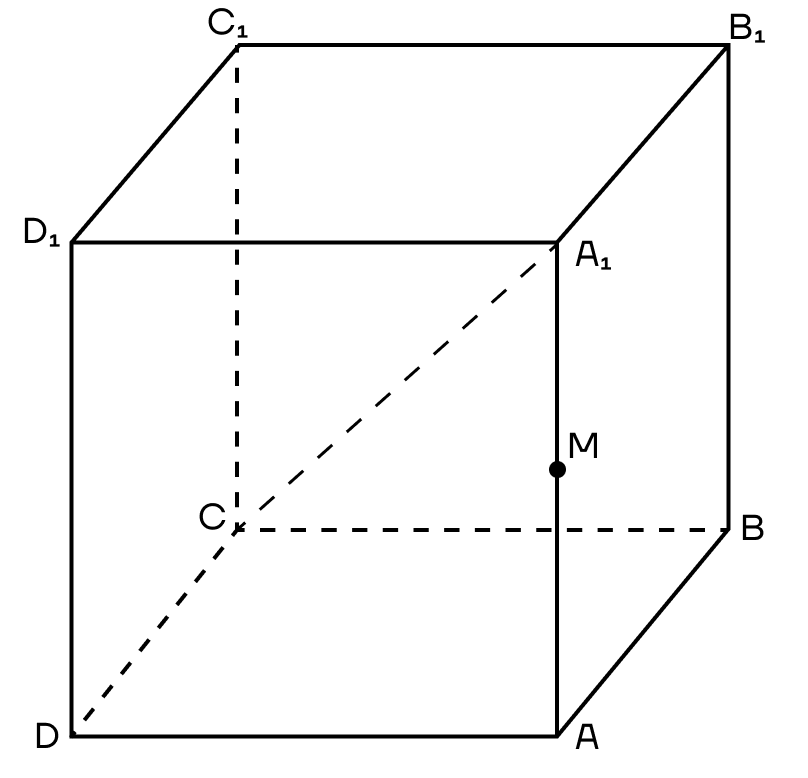
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
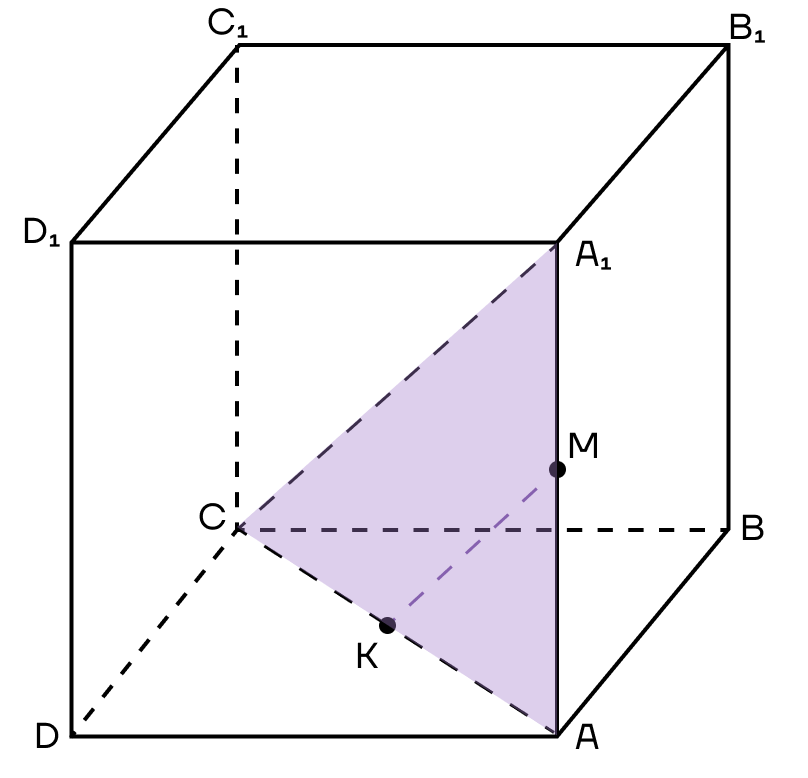
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
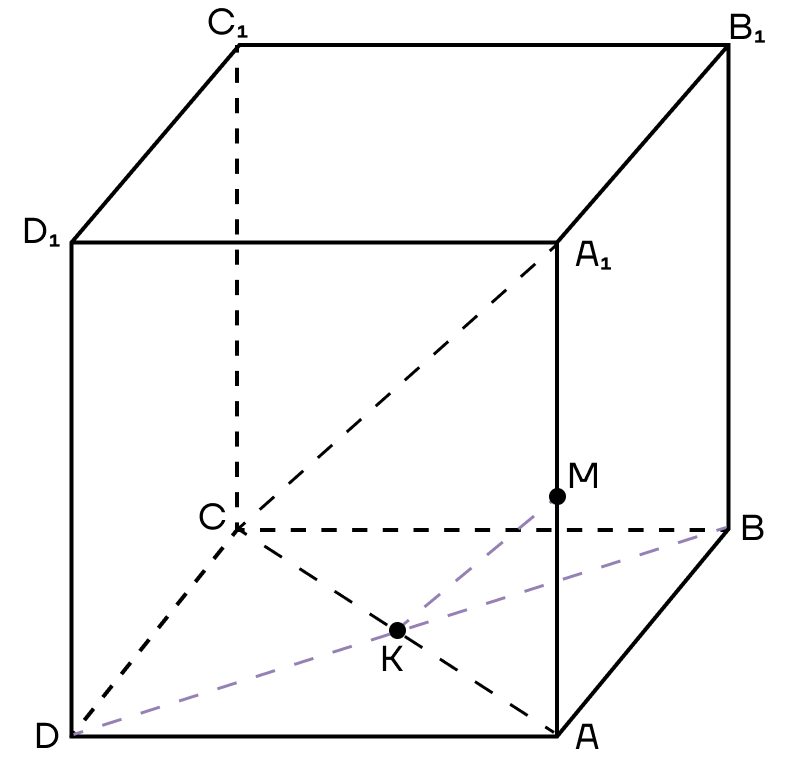
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Фактчек
- Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
- Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
- Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
- Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях. Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
- Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.
Проверь себя
Задание 1.
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?
- Треугольник;
- Четырехугольник;
- Шестиугольник;
- Произвольный многоугольник с любым количеством углов.
Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?
- Только в вершинах многогранника;
- На ребрах многогранника;
- Только на гранях многогранника;
- В любой точке на многограннике.
Задание 3.
Что такое след сечения?
- Продолжения сторон сечения;
- Вершины многоугольника, который образовывает сечение;
- Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
- Все вышеперечисленные варианты.
Задание 4.
Что можно сделать с точками, которые лежат на одной грани?
- Соединить;
- Ни в коем случае нельзя их соединять;
- Построить сечение, опираясь на две разные стороны, не соединяя стороны;
- Ни один из перечисленных вариантов.
Задание 5.
Как можно воспользоваться методом внутреннего проектирования?
- Произвольно переносить линии сечения в любых гранях;
- Произвольно переносить линии сечения в параллельных гранях;
- Перпендикулярно переносить линии сечения в перпендикулярных гранях;
- Параллельно переносить линии сечения в параллельных гранях.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4


 к списку статей
к списку статей