Вычисление вероятности
На этой странице вы узнаете
- Как кот может быть одновременно живым и мертвым?
- Возможно ли всегда одерживать победу в споре с монеткой?
- Если на экзамене по профильной математике рандомно отвечать на вопросы теста, какой шанс сдать экзамен?
Какова вероятность выиграть в лотерею? Исследователи посчитали: один на восемь миллионов. «Одержу победу или проиграю», — есть два варианта решения, приобретая билет с лотереей. Таким образом, вероятности встречаются у каждого в повседневной жизни. И не только при покупке лотерейного билета. Рассмотрим этот вопрос более подробно.

Вероятность
Перед выходом на улицу в пасмурную погоду каждый задумывается: брать ли с собой зонт. Анализируем прогноз погоды и видим, что вероятность осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он может сбыться, а может и нет. Никто не может точно угадать, какая погода будет завтра или на следующей неделе. Но каждый человек смотрит прогноз погоды, выходя из дома, чтобы примерно понимать, на какую погоду рассчитывать.
Теория вероятности – один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайные эксперименты относятся к тем, где исходы остаются скрытыми до момента их совершения. Например, подкидывая монетку, невозможно предугадать, будет ли выпадать орел или решка. Только когда мы ловим монетку, наблюдаем результат.
| Как кот может быть одновременно живым и мертвым? Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом. По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется, и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается, и кот останется жив. Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв. |
Разберем более подробно пример с монетой. Может произойти лишь два события:
- выпадет монета с орлом;
- выпадет монета с решкой.

Эти два события образуют совокупность событий.
Множество элементарных событий — все возможные результаты какого-либо эксперимента.
В упомянутом выше случае присутствует всего два. При бросании игральной кости окажется уже 6 доступных исходов. Различные элементарные события будут видоизменяться в зависимости от обстоятельств.
Предположим, мы с другом заключили пари на то,что выпадет орел. Это событие выгодно, так как мы выиграем пари. Второе событие является неблагоприятным,так как мы проиграем пари.
Как найти вероятность победы в споре? Необходимо разделить число благоприятных событий на общее число событий. Это классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получается формула.
\(P=\frac{m}{n}\)
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Число благоприятных исходов должно быть меньше или равно числу всех исходов. Если благоприятных исходов больше, чем всех исходов, то это означает,что найдены не все возможные события.
Если вероятность равна 1, то такие события обязательно произойдут. Другими словами, вероятность их наступления составляет 100%.
Также существует формула полной вероятности или формула Байеса.
Если события \(B_1, B_2, …B_n\) образуют полную группу событий и при наступлении каждого из них, событие А может наступить с некоторой условной вероятностью \(P_{B_1}\)(A), в таком случае вероятность наступления события А равна сумме произведений вероятностей каждого из событий \(B_1\) на соответствующую условную вероятность события А.
\(P(A)=P(B_1)*P_{B_1}(A)+P(B_2)*P_{B_2}(A)+…+P(B_n)\)
Рассмотрим наиболее частую задачу на вероятность, встречающуюся на ЕГЭ по профильной математике в задании №3.
Задание. Игральную кость бросают два раза. Найдите вероятность того, что выпавшие значения окажутся нечетными. Ответ округлите до сотых.
Решение. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно \(6 * 6 = 36\). Благоприятны для события только исходы, когда выпадает 1, 3 и 5 очков. Таких граней 3, но не стоит забывать, что игральную кость бросили два раза, следовательно, благоприятных исходов \(3*2=6\). Значит, вероятность, которую мы ищем, равна:
\(\frac{N_{благ}}{N_{общ}}=\frac{6}{36}=0,166…\)
Поскольку ответ нужно округлить до сотых, достаточно посчитать до трех цифр после запятой.
Ответ: 0,17

| Возможно ли всегда одерживать победу в споре с монеткой? Можно, но нужно учитывать определенные условия для достижения желаемого результата. Один из вариантов – изменить формулировку условий: «Если выпадет орел, то я выиграю, если выпадет решка, то ты проиграешь». В этом случае, вероятность выигрыша будет равна \(P = \frac{2}{2} = 1\), что гарантирует нам победу в данном споре. Однако вероятность не сводится к такой простой схеме, и здесь тоже предусмотрена возможная ловушка. В редких случаях возникает третий исход – монетка может упасть на ребро. Вероятность такого события составляет \(\frac{1}{6000}\). Это означает, что при миллионе бросков монетки, ребро может выпасть 150 раз, или, другими словами, раз в 2 дня, если мы будем подкидывать монетку каждый день по 8 часов в течение года. Чтобы монетка упала на ребро два раза подряд, нам потребуется проводить подбрасывания с такой же интенсивностью примерно 35 лет. |
Вероятность всегда будет меньше или равна 1, но больше 0. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. В отеле на входе стоит ваза с конфетами. В ней находится 56 конфет с клубничным вкусом, 49 с ежевичным и 35 с ананасовым. Один из гостей не глядя берет конфету. Какова вероятность того, что он возьмет конфетку с ежевичным вкусом?
Решение. Найдем количество конфет в вазе: \(56+49+35=140\). Вероятность вытащить конфету с ежевичным вкусом будет равна:
\(\frac{49}{140}=0,35\)
Выразим в процентах:
\(0,35*100%=35%\)
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Для выражения вероятности в процентах можно использовать следующую формулу.
\(P=\frac{m}{n}*100%\)
Но что делать, если необходимо найти вероятность более сложного эксперимента? Первое, что нужно сделать, — определить, какое событие перед вами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
На игровом кубике может произойти шесть событий. Эти события являются частью общей группы событий, в которую они входят.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
При подбрасывании монеты может выпасть орел или решка. То есть вся группа событий включает в себя два события.
Мы подбросили монету, и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Будет решка. Эти события будут называться противоположными друг другу.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Пусть событие «выпала монета с решкой» будет обозначено как A. Противоположное событие «выпала монета с орлом» — как \(\overline{A}\).
Обратим внимание на то, что вероятность события \(A\) равна \(\frac{1}{2}\), как и вероятность события \(\overline{A}\). Посчитаем сумму данных событий.
\(\frac{1}{2}+\frac{1}{2}=1\)
Таким образом, выводится связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей равна единице.
\(P(A)+P(\overline{A})=1\)
Какие еще есть примеры диаметрально противоположных событий? Солнечная погода и дождливая погода. Если происходит одно, то другое не происходит.
Также события могут объединяться или пересекаться.
Объединение и пересечение событий
Предположим, что есть два события: сегодня идет снег и сегодня идет дождь. Что произойдет, если мы объединим эти события?
Объединение событий — событие, состоящее из всех элементарных исходов в пользу хотя бы одного события.
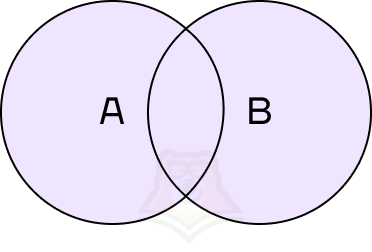
В этом случае событие может быть удовлетворено любым исходом, будь то снег или дождь.
Объединение событий обозначается знаком \(\cup\). Объединение событий А и В можно записать как \(A\cup B\).
Рассмотрим несколько иной пример. Первое событие — Илья получает пятерку по физике, второе событие — Антон получает пятерку по физике. Если они оба получили пятерки по физике, то как назвать это событие?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.
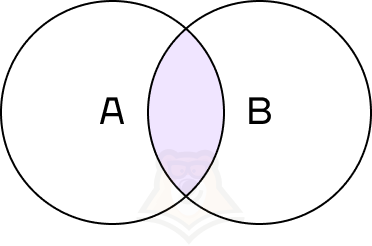
Пересечение событий обозначается знаком \(\cap\). Пересечение событий А и В можно записать как \(A\cap B\).
Если пересечение событий А и B невозможно, то они называются несовместными (непересекающимися).
\(A\cap B=\oslash \)
Если же все наоборот, события называются совместными или не пересекающимися, о них поговорим далее.
Несовместные и совместные события
Рассмотрим два события: «чайник исправно работает» и «чайник поломан». Могут данные события происходить одновременно? Нет, поскольку одно из них сразу исключает второе.
Такого рода события называются несовместными. Название говорит само за себя, события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. Какова вероятность получить билет по любой из этих тем теста?

Представим билет в виде схемы. Заметим, что нам необходимо объединить две из трех окружностей, то есть сложить вероятности.
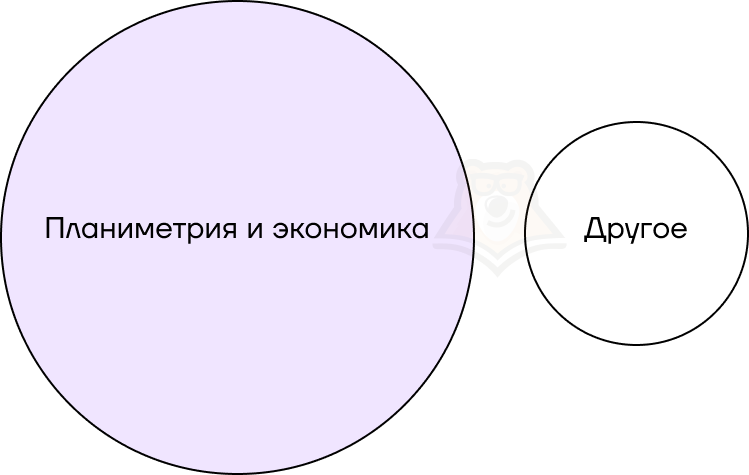
Данная вероятность будет равна \(0,5+0,3=0,8\).
Стоит сформулировать определение суммы вероятностей двух несовместных событий.
Если события A и B несовместны,то вероятность их сочетания равна сумме их вероятностей.
\(P(A\cup B)=P(A)+P(B)\)
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят разговором с покупателем. Значит ли это, что второй консультант тоже занят?Нет, поскольку они работают независимо друг от друга. Если первый консультант занят, то второй может быть занят,а может и не быть.
Рассмотрим два различных события при бросании игральных костей. Пусть событие A — «выпадет 2», а событие B — «выпадет четное число».
Найдем вероятность события А: \(\frac{1}{6}\).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6}=\frac{1}{2}\)
Исключают ли события А и В друг друга? Нет. Это объясняется тем, что если произойдет событие A, то произойдет и событие B. Если событие B произойдет, то существует вероятность того, что произойдет и событие A.
Используйте пример с окружностью для нахождения суммы совместных событий. При их наложении в середине образуются два слоя. Это можно проверить, наложив друг на друга два листа бумаги.
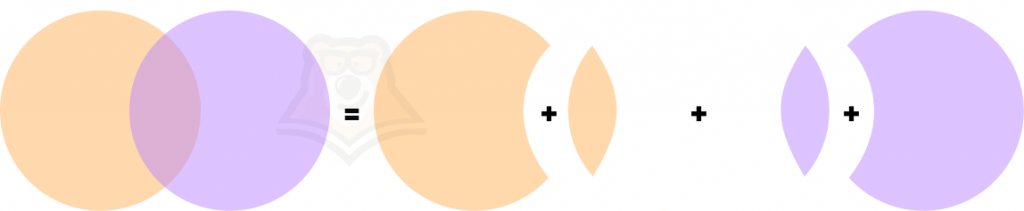
А нужно получить вот такую картину:

Поэтому, чтобы соединить две окружности, необходимо исключить одну из них, находящуюся в середине.
Если события A и B совместны, то вероятность их соединения равна сумме вероятностей их пересечения, исключая вероятность их пересечения.
\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)
Разберем пример задания №4 из ЕГЭ по профильной математике.
Задание. В торговом центре стоит два одинаковых автомата с кофе. Вероятность того, что к концу дня кофе закончится в одном из автоматов, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,15. Какова вероятность того, что к концу дня кофе закончится хотя бы в одном автомате?
Решение. Событие А — кофе закончится в первом автомате, B — кофе закончится во втором автомате \(\Rightarrow P(A) = P(B) = 0,4\)
\(P(A\cup B) = 0,8\)
По смыслу задачи события А и В являются совместными. Нужно применить формулу сложения вероятностей совместных событий.
\(P(C)= P(A\cup B)= P(A)+P(B)-P(A\cap B)= 0,4+0,4-0,16=0,64\)
Ответ: 0,64
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью «или». Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Также события могут зависеть друг от друга или не зависеть.
Независимые и зависимые события
Зайдем в магазин, чтобы купить булочку. Булочки продаются по две штуки, упаковка непрозрачная, поэтому булочек не видно до открытия.
Известно, что на фабриках, производящих булочки, из каждых 100 булочек подгорает пять. Другими словами, 95 из 100 булочек не сгорают. Следуя классическому определению вероятности, мы знаем, что вероятность того, что каждая булочка не сгорит, равна \(\frac{95}{100} = 0,95\).
Какова вероятность того, что в упаковке находятся только несгоревшие булочки? Как найти вероятность сразу для двух булочек?
Зависимы ли булочки друг от друга? Если одна из булочек в упаковке сгорит, то другая не обязательно сгорит. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна \(Р(А) = 0,95\), а вероятность для второй булочки будет равна \(Р(В) = 0,95\).
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
\(P(A\cap B)=P(A)*P(B)\)
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется \(P=0,95*0,95=0,9025\).
В каком случае нужно пользоваться этой формулой? Нужно подставить союз «и».
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Другой пример. На разных этажах здания стоят два автомата с кофе. Если один из них выходит из строя, то работа второго автомата не зависит от работы первого.
Однако если автоматы находятся рядом друг с другом и подключены к одной розетке, то существует вероятность того, что при выходе из строя одного из них, розетка выйдет из строя и второй автомат тоже выйдет из строя. Такие события являются зависимыми, и наступление одного из них зависит от наступления другого.
В небольшом мешке лежат кубики: два из них оранжевые, а пять — фиолетовые. Два раза из мешка достают кубики. Какая вероятность того, что кубик, который достанут во второй раз, будет именно фиолетового цвета ?
Нужная последовательность может быть в двух случаях:
- первым достанут кубик фиолетового цвета, затем снова достанут фиолетовый кубик;
- первым достанут оранжевый кубик, а вторым фиолетовый.
Рассмотрим первый случай. Вероятность первым достать кубик фиолетового цвета равна \(\frac{5}{7}\). После этого действия в мешке останется еще шесть кубиков, четыре из них будут иметь фиолетовый цвет..
Вероятность достать во второй раз кубик фиолетового цвета равна \(\frac{5}{7}*\frac{4}{6}=\frac{20}{42}=\frac{10}{21}\).
Разберем второй вариант. Вероятность того, что в первый раз вытащат кубик оранжевого цвета, равна \(\frac{2}{7}\). В мешке останется шесть кубиков, пять из них будут фиолетового цвета.
В таком случае вероятность достать вторым кубик фиолетового цвета будет равна \(\frac{2}{7}*\frac{5}{6}=\frac{10}{42}=\frac{5}{21}\).
Данный пример достаточно точно показывает, что вероятность напрямую зависит от того, кубик какого цвета попался первым. Следовательно, эти события являются зависимыми.
В чем различие между зависимыми и независимыми событиями? Если после первого события благоприятный исход и количество всех исходов изменяются, то такое событие является зависимым. Если благоприятный исход и количество всех исходов не изменяются, то такое событие является независимым.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.

Условная вероятность обозначается \(P(B|A)\). В данном примере условная вероятность рассчитывается как вероятность того, что кубик фиолетового цвета достанут вторым.
Найти вероятность двух зависимых событий. Уравнение аналогично уравнению для независимых событий. Однако на этот раз необходимо применить условную вероятность.
Вероятность наступления двух зависимых событий равна произведению вероятности одного из них и условной вероятности другого, если первое событие уже произошло.
\(P(A\cap B)=P(A)*P(B|A)\)
В математике существует формула, которая позволяет избавиться от большого количества вычислений. Поговорим о ней ниже.
Дисперсия
Дисперсия в физике означает разложение света на отдельные цвета, когда он проходит через призму. Зная этот факт, можно догадаться что же такое дисперсия в математике.
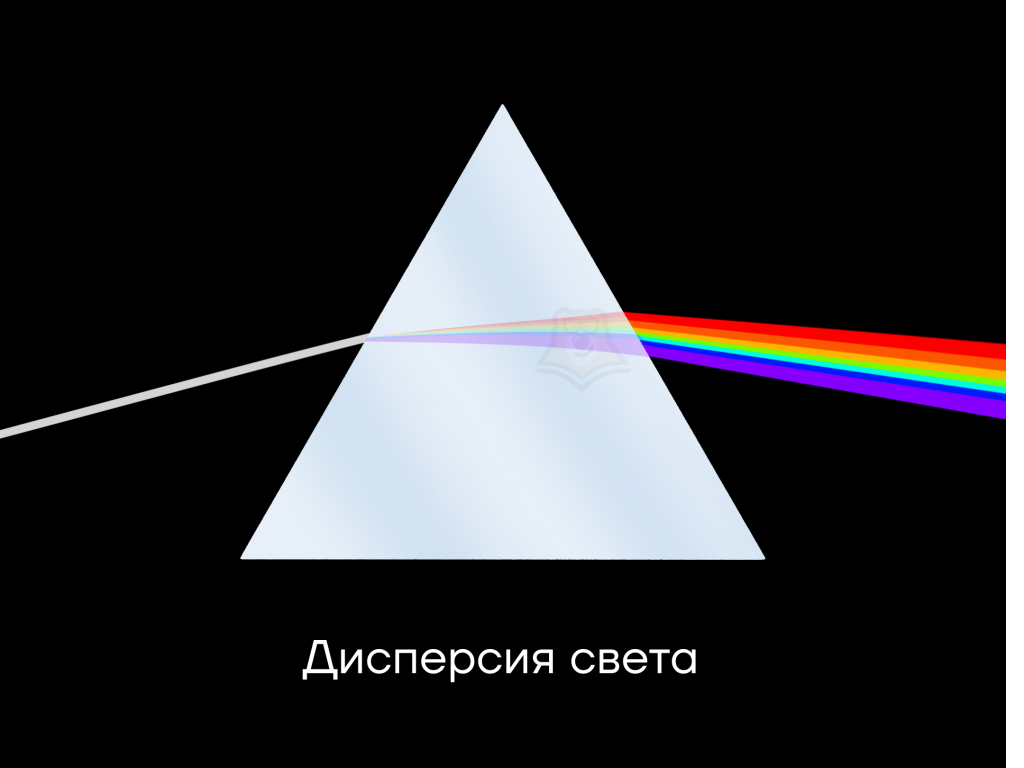
Слово «дисперсия» означает «рассеяние», то есть дисперсия характеризует рассеяние значений случайной величины около ее математического ожидания.
Математическое ожидание — это среднее значение случайной величины, то есть, проще говоря, это ожидаемый результат (рассчитанный по вероятностям возможных событий).
Точка, вокруг которой считают разброс, — это обычно среднее арифметическое из выборки, математическое ожидание или какое-то целевое значение. Проще говоря, дисперсия показывает, насколько велика вероятность того, что следующее значение будет сильно отличаться от среднего. Если, например, разброс между ответами на какой-то тестовый вопрос, в качестве центральной точки можно взять правильный ответ.
Чем больше разбросаны значения в наборе данных, тем выше дисперсия. Например, две группы одного направления учатся по 100-балльной системе. В первой группе студенты в конце семестра набирают 80-100 баллов. Во второй группе количество баллов варьируется от 30 до 100. Соответственно, во второй группе разброс баллов более обширный, значит и дисперсия будет выше.
Дисперсия случайной величины Х вычисляется по формуле:
\(D(Х)=M(X-M)^2,\)
где Х — случайная величина, а M — математическое ожидание.
Пример. Задан следующий закон распределения случайной величины Х:
| \(x_i\) | 0 | -0,5 | 0,2 |
| \(p_i\) | 0 | 0,4 | 0,1 |
В таблице \(x_i\)— значение случайной величины, а \(p_i\)— вероятность значения случайной величины. Другими словами, это такое же нахождение вероятности событий (случайной величины), результаты которого отображены в табличной форме.
Для начала нужно продолжить таблицу и найти математическое ожидание \((М(Х))\) и математическое ожидание от \(X^2((M( X^2))\)
| \(x_i\) | 0 | -0,5 | 1 |
| \(p_i\) | 0 | 0,4 | 0,2 |
| \(p * x\) | 0 | -0,2 | 0,2 |
| \(p * x^2\) | 0 | 0,2 | 1 |
Далее требуется найти математическое ожидание
(М(Х)=\sum^{n}_{i=1}x_ip_i )\(M(X)=0-0,2+0,2=0\)
\(М(Х^2)=0+0,2+1=1,2\)
Получив все недостающие значения, можно найти дисперсию, применив формулу
\(D(Х)=M(X-M)^2 =1,2-0=1,2\)
Ответ: 1,2
Если из дисперсии Х выразить квадратный корень, то можно узнать стандартное отклонение.
Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. Простыми словами это мера того, насколько разбросан набор данных.
Чем меньше стандартное отклонение, тем более плотно «сгруппированы» данные вокруг центра (среднего). И наоборот, чем отклонение больше, тем больше разброс значений. На графиках величина стандартного отклонения изображается с помощью «горки», вершина которой лежит на линии математического ожидания. Чем выше и круче горка, тем меньше стандартное отклонение.
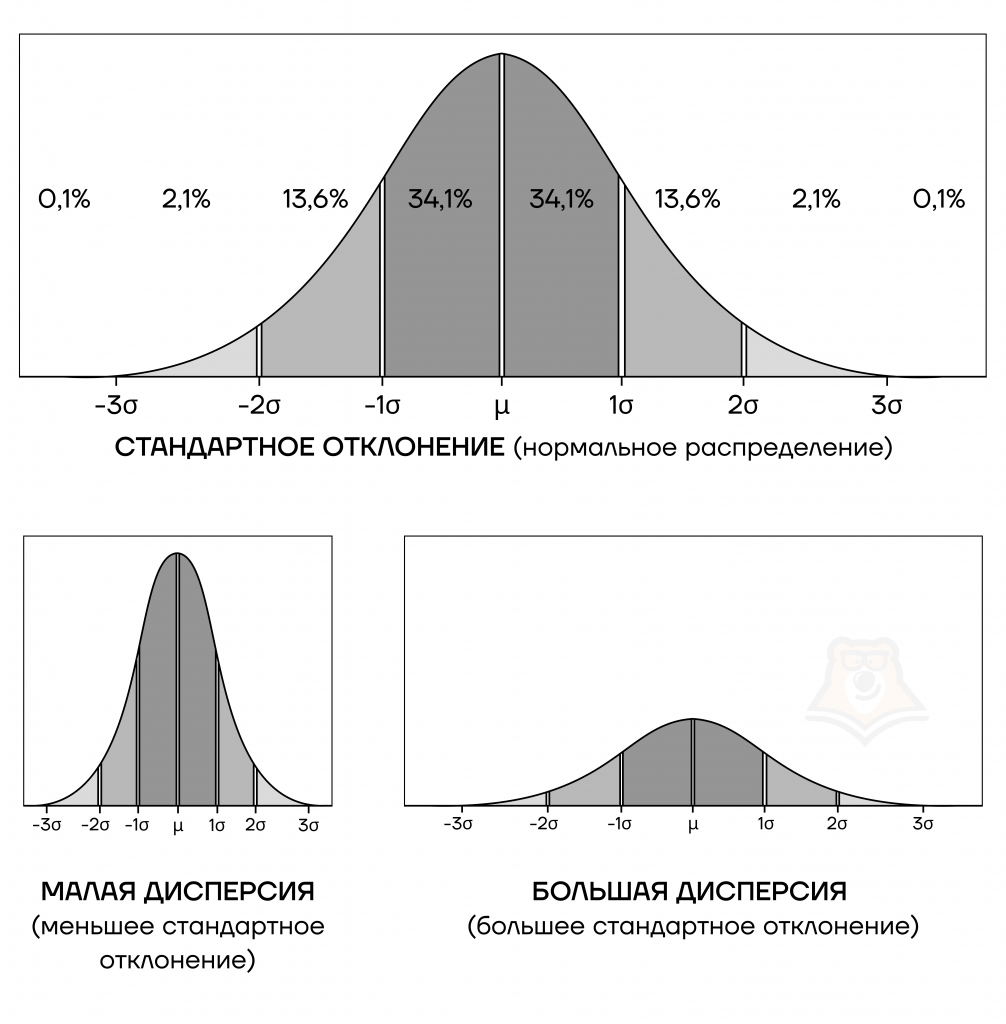
Вычисляя стандартное отклонение, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение. Таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение рассчитывается по формуле:
\sigma=\sqrt{\frac{\sum^{n}_{i=1N}(х_i-)^2}{N}}, где\(x_i\) — величина отдельного значения
\(\mu \) — среднее арифметическое
\(N\) — размер выборки
Пример. В таблице записаны данные о запасе товара на предприятии Z.
| 1 день | 2 день | 3 день | |
| Предприятие Z | 5 | 13 | 12 |
Начать можно с нахождения среднего арифметического для данной выборки, для этого нужно сложить все запасы и разделить на количество дней.
\(\mu=\frac{5+13+12}{3}=10\)
Далее от каждого значения выборки нужно отнять среднее арифметическое и возвести в квадрат полученные значения.
\((x_1-\mu)^2=(5-10)^2= 25\)
\((x_2-\mu)^2=(13-10)^2= 9\)
\((x_3-\mu)^2=(12-10)^2= 4\)
После этого нужно посчитать сумму полученных значений и разделить ее на размер выборки.
\(\frac{\sum (x_i-\mu)^2}{N}=\frac{25+9+4}{3} \approx 12,7\)
Теперь остается лишь извлечь квадратный корень.
\(\sqrt{\frac{\sum (x_i-\mu)^2}{N}}=\sqrt{12,7} \approx 3,6\)
Однако вероятность не всегда возможно рассчитать, зная только классическое определение.
Геометрический смысл вероятностей
Классическое определение вероятности очень ограниченно. Для получения верных данных необходимо производить большое количество действий. Также оно применимо только к пространствам элементарных исходов, что резко сужает круг задач, которые могут быть решены.
Чтобы избежать недостатки классического определения вероятности, ввели геометрический смысл вероятности — вероятность попадания точки в область (часть плоскости, отрезок и так далее).
Вероятность наступления некоторого события А равна:
\(Р(А)=\frac{g}{G}\),
где G — геометрическая мера, обозначающая общее число всех возможных и равновозможных исходов данного события, а g — геометрическая мера, выражающая количество благоприятных для события А (чаще всего в качестве данной меры выступает длина и площадь, иногда — объем).
Отличается формула геометрической вероятности от классической лишь тем, что в ней вместо обычных чисел используются геометрические меры.
Пример. В круг радиуса R = 25 бросается точка. Найти вероятность ее попадания в квадрат, вписанный в круг. В данном случае, никак не решить задачу, используя классическое определение вероятности. Тогда к нам на помощь приходит геометрия. Зная всего несколько формул, можно с легкостью решить задачу. Эти формулы вы можете найти в статье «Вписанная и описанная окружность».
\(P(A)= \frac{2R^2}{\pi R^2}\),
где \(2R^2\) — площадь квадрата, а \(\pi R^2\) — площадь круга.
Получившуюся формулу можно упростить: сократить на \(R^2\).
\(P(A)=\frac{2}{\pi}\)
Задачи с более сложным условием можно решать, используя графический метод.
Использование дерева вероятностей
Деревом вероятностей называется графический метод, который показывает стратегию решений последовательно и предполагает последовательности действий при всех возможных случайных обстоятельствах.
Построение дерева вероятностей начинается с первого решения и продолжается через множество последовательных событий. Чаще всего вероятностные события обозначаются кружками, а принимаемые решения квадратиками. Ответвления от квадратиков — стратегии, а ответвления от кружков — внешние условия. Ответвления появляются при каждом событии до тех пор, пока не закончатся все последовательности решений и вытекающие из них события.
Чаще всего метод дерева решений используют в более сложных задачах. Рассмотрим одну из них.
Задача. На дне рождения разрезали торт на всех гостей поровну, но внезапно подошел опаздывающий Ваня. Все решили поделиться с ним. Настя отрезала \(\frac{1}{3}\) от своего куска, Лиза \(\frac{1}{4}\), а Никита — половину. Какую часть от торта получил Ваня?
Решение. Сначала торт разрезали на трех гостей поровну:
Затем пришел опоздавший Ваня:
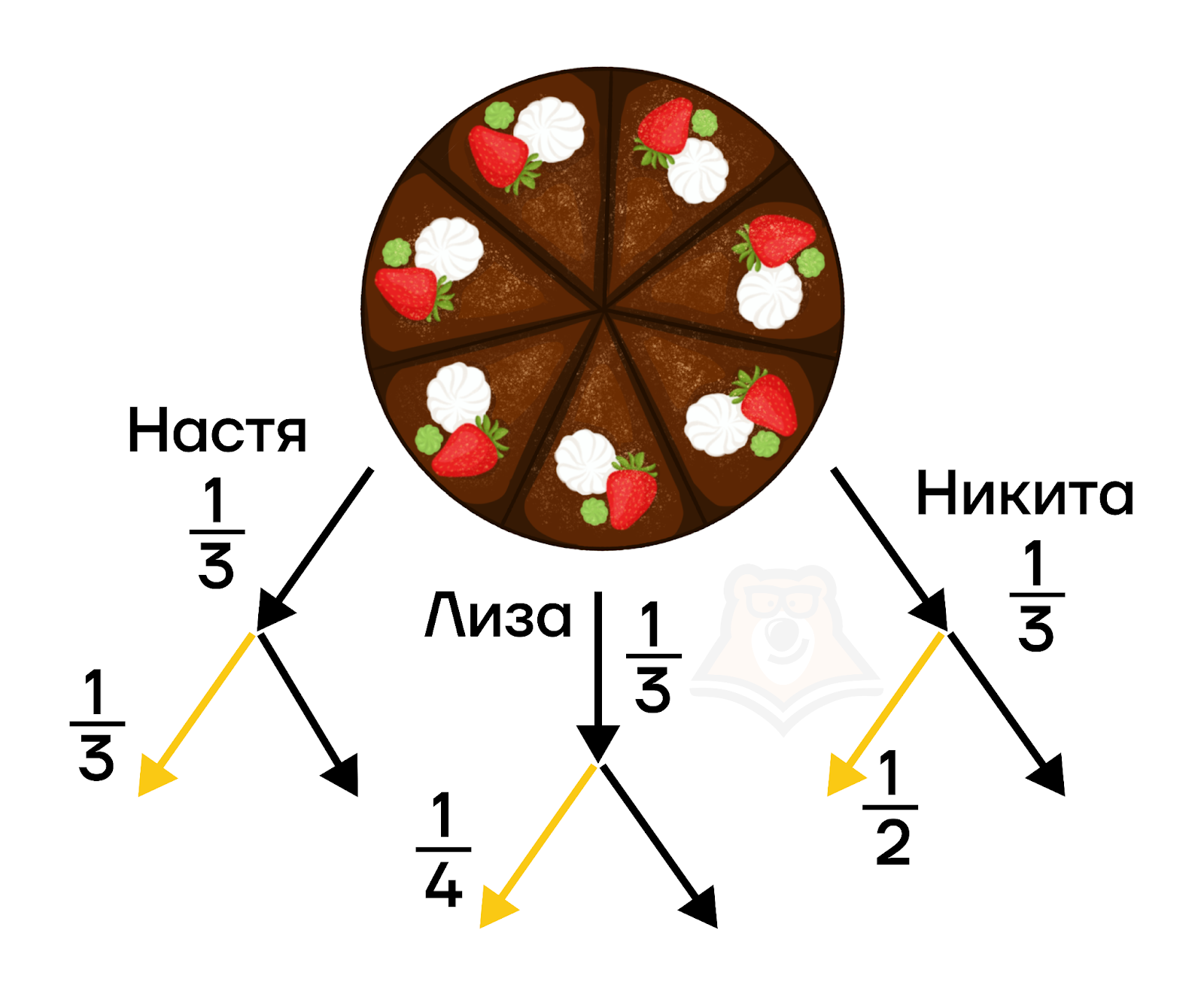
Чтобы найти дробь от числа, нужно число умножить на эту дробь.
Получается, Настя отдала Ване \(\frac{1}{3}*\frac{1}{3}=\frac{1}{9}\), Лиза — \(\frac{1}{3}*\frac{1}{4}=\frac{1}{12}\), а Никита \(\frac{1}{3}*\frac{1}{2}=\frac{1}{6}\).
Чтобы найти, какая часть торта досталась Ване, остается только сложить все дроби.
В итоге, Ваня хоть и опоздал, но получил \(\frac{1}{9}+\frac{1}{12}+\frac{1}{6}=\frac{13}{36}\) часть торта.
При поиске вероятности события нужно искать, какую часть от общего числа исходов составляют благоприятные. Если в задаче описано множество последовательных событий, и каждое из них зависит от исхода предыдущего, ее можно решать с помощью данного графического метода.
Для упрощения решения задач существует формула, которая избавляет нас от большого числа вычислений. Поговорим о ней ниже.
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда \(p=\frac{1}{6}\).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. \(q=\frac{5}{6}\).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
\(Pn(k)=C_n^k*p^k*q^{n-k}\)
Множитель \(C_n^k\) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
\(P_8(3)=C_8^3*(\frac{1}{6})^3*(\frac{5}{6})^5=\frac{8!}{5!3!}*\frac{1}{6^3}*\frac{5^5}{6^5}=\frac{6*7*8}{1*2*3}*\frac{5^5}{6^8} \approx 0,1\).
| Если на экзамене по профильной математике рандомно отвечать на вопросы теста, какой шанс сдать экзамен? Первая часть экзамена по профильной математике включает в себя 11 заданий. Чтобы перейти порог и сдать экзамен, нужно набрать хотя бы 27 тестовых баллов или 6 первичных. Попасть хотя бы в половину заданий будет трудно, даже используя сверхъестественные способности. Стоит учесть, что на экзамене по математике нет ни одного задания с вариантом ответа, в отличие, например, от экзамена по истории. Следовательно, вариантов ответа на любое задание приближенно к бесконечности. Можно сделать вывод, что сдача экзамена по математике путем рандома, к сожалению, слишком близка к нулю. Так что, если цель — это сдача экзамена на достойный балл, придется потрудиться. |

Прочитав данную статью, вы наверняка станете намного лучше разбираться в вероятностях. Хотя на экзамене задачам с расчетом вероятности отведено не так много заданий, стоит разбираться в тонкостях этой темы. Еще больше интересного вы сможете узнать в статье «Основы комбинаторики».
Термины
Среднее арифметическое – величина, которая вычисляется путем деления суммы всех значений на их количество.
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: \(P(A\cup B)=P(A)+P(B)\). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле \(P(A\cap B)=P(A)*P(B)\). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. \(P(A\cap B)=P(A)*P(B|A)\).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
- Дисперсия — мера разброса набора чисел от их среднего значения. Точка, вокруг которой считается разброс, чаще всего определяется как среднее арифметическое либо математическое ожидание.
- Стандартное отклонение — это мера того, насколько разбросан набор данных.
- Геометрический смысл вероятности — вероятность попадания точки в часть плоскости, отрезок,
- Дерево вероятностей — графический метод решения задач, при котором используется стратегия решений последовательно при всех возможных случайных событиях.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Даша перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1


 к списку статей
к списку статей





