Законы Кеплера

На этой странице вы узнаете

• Почему кометы не возвращаются?
• Как часто нам помогает парабола в жизни? 
• Сколько лет в году? 

Часто ли вы смотрите на звездное небо? Наверняка, да. Эти далекие мерцающие огни, бескрайние просторы и холодная пустота не могут не вдохновлять. Никто не смеет сомневаться, что в космосе холодно, но так ли он пуст? 

К сожалению или к счастью, нет. Космическое пространство наполнено различными объектами, начиная с частиц и заканчивая гигантскими галактиками, полными звезд, планет и черных дыр. Но по каким законам происходит их движение? Все это мы непременно сегодня выясним.

Законы Кеплера

Еще с самых древних времен наблюдение за небесными телами привлекало людей из самых разных стран. Так, например, классификацию звезд по яркости придумал древнегреческий астроном Гиппарх во Ⅱ веке до нашей эры. А в конце ⅩⅥ века датский астроном Тихо Браге собрал самый подробный журнал наблюдений за движениями небесных объектов. Благодаря этим данным через несколько лет великий немецкий ученый Иоганн Кеплер вывел 3 закона, которым подчиняются все тела в космическом пространстве. 

Но прежде, чем мы начнем говорить о них, давайте вспомним геометрию, без нее дальше будет неинтересно.

Конические сечения

Что будет, если мы возьмем конус и начнем разрезать его под разными углами? Мы получим конические сечения. Всего их 3 вида: эллипс, парабола и гипербола. 

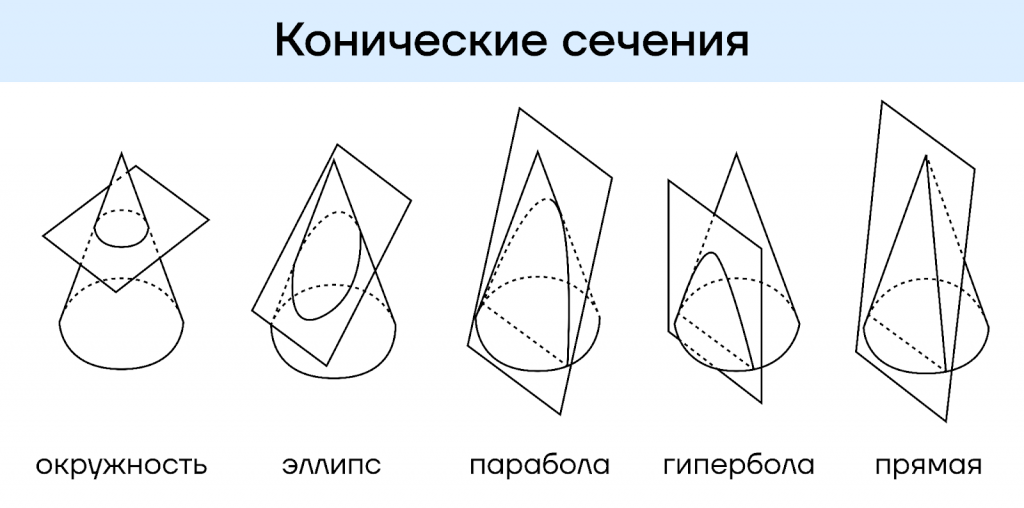
Отдельно не принято выделять окружность и прямую, так как это частные случаи эллипса. Да-да, прямая и окружность не так уж и сильно отличаются. Скоро узнаем почему. Для того чтобы отличать сечения друг от друга, вводят такую величину как эксцентриситет.

Эксцентриситет (e) – числовая характеристика конического сечения, показывающая степень его отличия от окружности.

В зависимости от вида конического сечения эксцентриситет принимает следующие значения: 

окружность	e = 0
эллипс	0 < e < 1
парабола	e = 1
гипербола	e > 1
прямая	e = \(\infty\)

Откуда взялись эти значения?
У любого конического сечения есть характерные величины, давайте на них остановимся подробнее. 

Величины конических сечений

• Эллипс

Что будет, если мы прикрепим две булавки, натянем между ними нитку и будем оттягивать эту нитку, описывая подобие окружности? Полученная фигура будет напоминать нам эллипс. 

Формально эллипс можно определить следующим образом.

Возьмем на плоскости две точки и назовем их фокусами. Выберем еще одну произвольную точку и посчитаем сумму расстояний от нее до первого и второго фокуса. Затем выберем все точки с такой же суммой. Вот мы и получили эллипс.

Все мы отлично помним, что окружность характеризуется своим радиусом (R). 

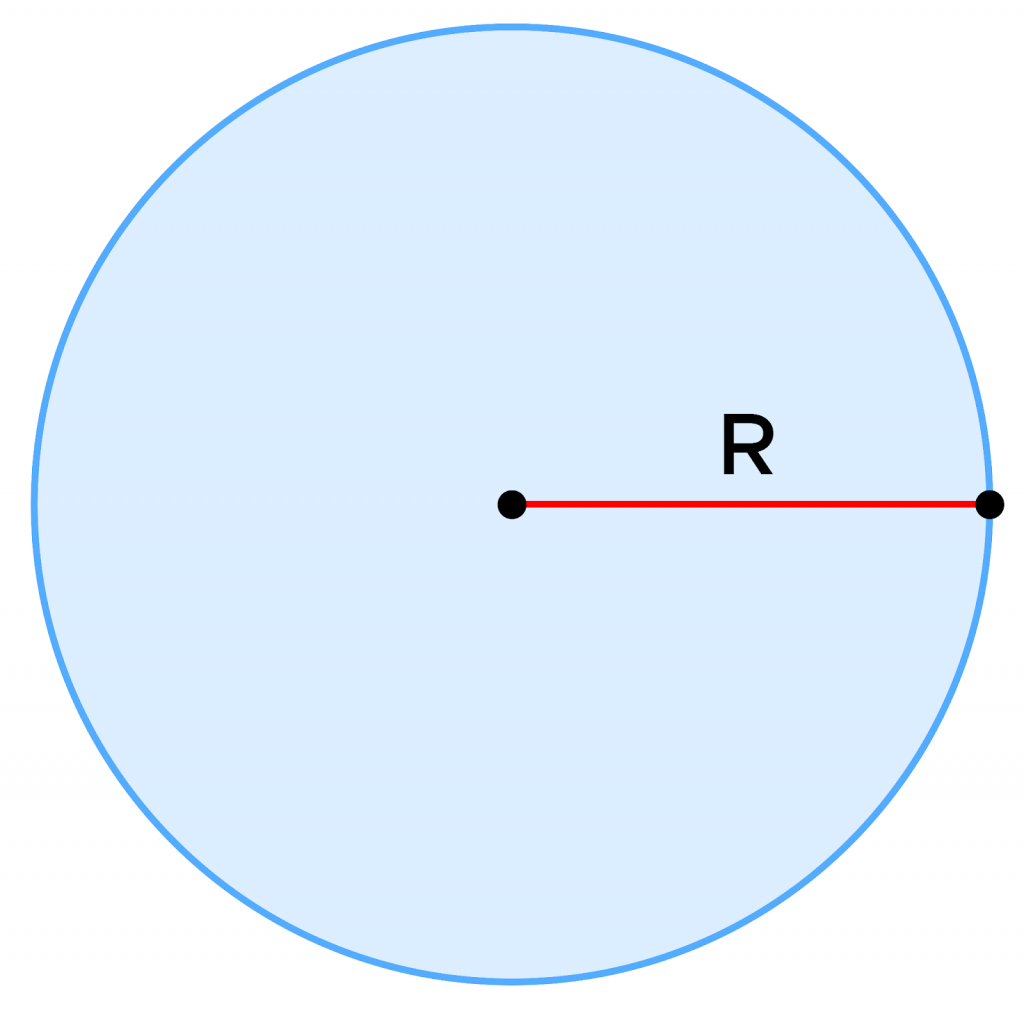
В случае эллипса его точки не расположены на одинаковом расстоянии от центра, и потому использовать понятие радиуса здесь мы не можем. Однако вполне достаточно двух полуосей: малой (b) и большой (a). Это будут основные параметры эллипса и, забегая вперед, почти любого конического сечения.

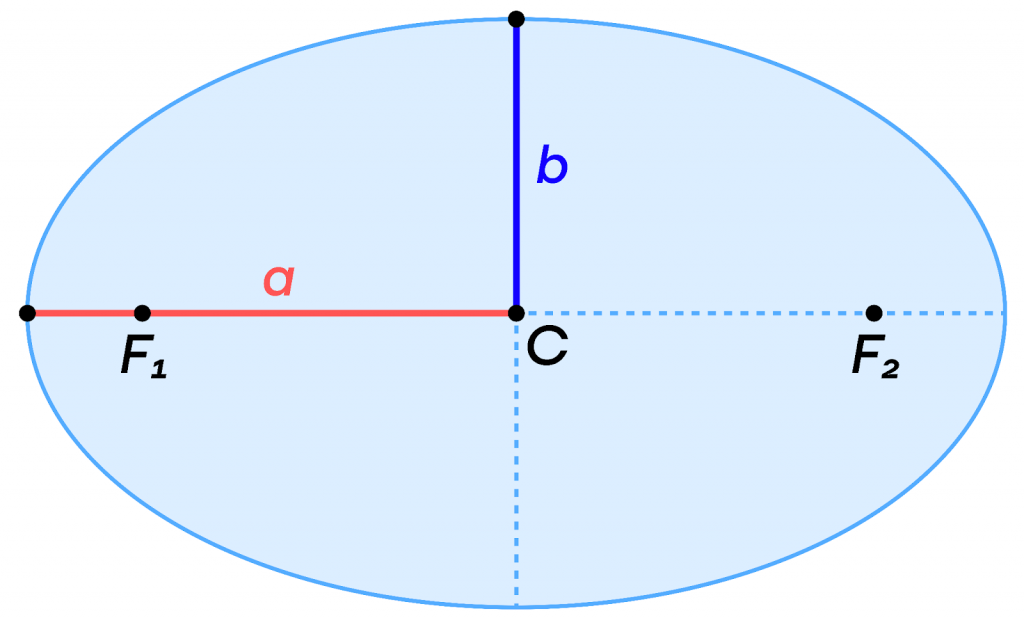
Формула эксцентриситета конических сечений, для которых введены полуоси, выглядит следующим образом: 

\(e = \sqrt{1-\frac{b^2}{a^2}}\)
\(e\) — эксцентриситет.
\(a\) — большая полуось.
\(b\) — малая полуось.

Что нам мешает рассмотреть окружность в качестве специфичного эллипса? Да собственно ничего!

Несложно заметить, почему у окружности эксцентриситет равен нулю, ведь в роли большой и малой полуоси выступает радиус.

\(e = \sqrt{1 — \frac{b^2}{a^2}} = \sqrt{1- \frac{R^2}{R^2}} = \sqrt{1 — 1} = 0\)

Также оба фокуса у нее совпадают с центром. Потому окружность является частным случаем эллипса. 

Можно ли такой же трюк провернуть с прямой? Да кто же нам помешает! Устремим малую полуось эллипса к нулю, а большую – к бесконечности. Вот мы и получили прямую из эллипса. Итак, еще раз, прямая является вырожденным эллипсом, у которого малая полуось равна нулю, а большая стремится к бесконечности. Почему тогда эксцентриситет прямой равен бесконечности, а не единице? 

Выше мы упомянули, что хоть полуоси и являются основными характеристиками конических сечений, но введены они не для каждого из них. Так, у параболы, о которой мы будем говорить ниже, полуоси отсутствуют. Аналогично не существует полуосей у прямой. Мы можем получить прямую из эллипса сжатием по одной оси и удлинением по другой, но такая прямая не будет являться коническим сечением по определению, а будет вырожденным эллипсом. У прямой, которая является коническим сечением, полуосей нет.

Однако, что важно, эксцентриситет по своему смыслу является мерой замкнутости кривой. Самой замкнутой кривой является окружность, и ее эксцентриситет 0, а самой открытой кривой является прямая, потому ее эксцентриситет бесконечность по определению. 

• Парабола

Теперь рассмотрим параболу. Возьмем на плоскости фокус и прямую, называемую директрисой. Все точки, равноудаленные от фокуса и директрисы, образуют параболу. В силу такого определения полуоси параболы не вводят, а оперируют лишь директрисой.

• Гипербола

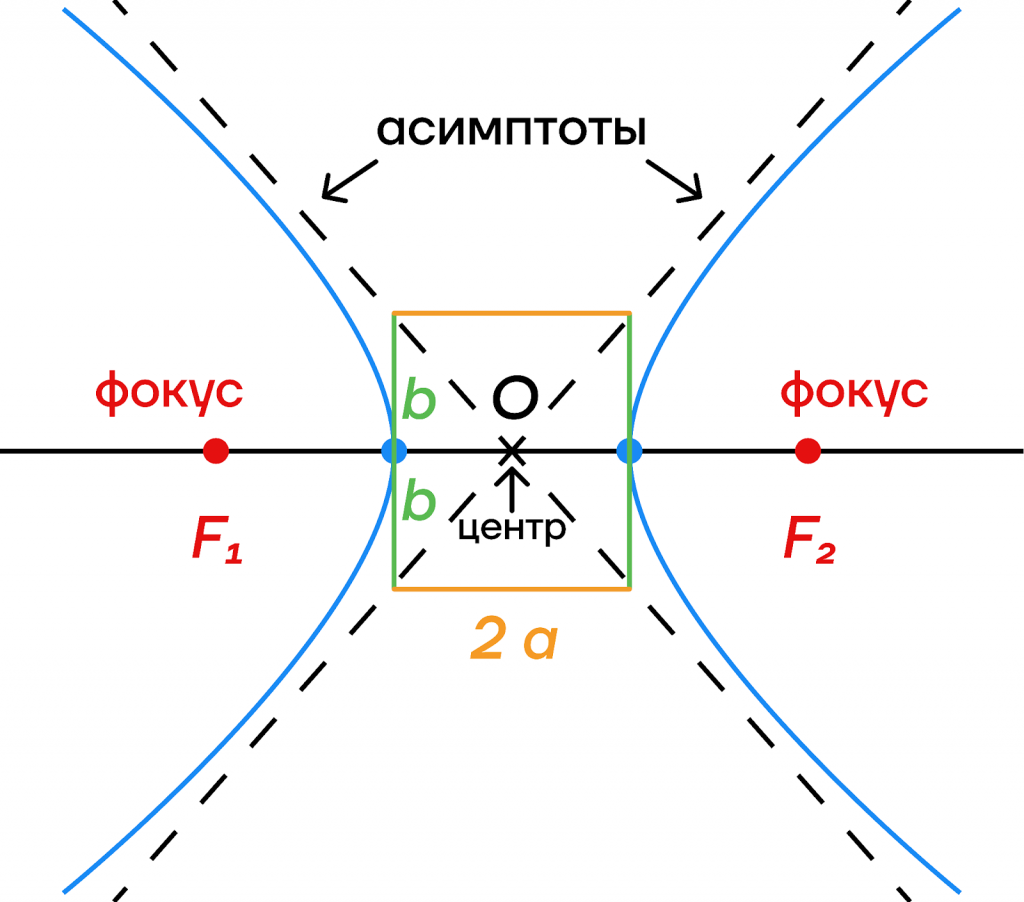
Нарисуем прямоугольник со сторонами 2a и 2b, затем проведем в нем диагонали, они будут асимптотами. Затем проведем кривую, огибающую наши асимптоты, то есть стремящуюся к ним на большом удалении от прямоугольника. Это и будет гипербола.

Гипербола обладает полуосями, они в точности являются сторонами нашего прямоугольника, деленными пополам. Особенность гиперболы в том, что ее большая полуось считается отрицательной. Конечно, это лишь математическая формальность, ведь расстояние никак не может быть отрицательным, но это произошло из-за того, что полуось отсчитывается не внутрь кривой, а наружу. Также гипербола обладает асимптотами, про которые мы говорили выше.

Почему кометы не возвращаются?  Появление каждой новой кометы – это целое событие в мире астрономии. Прилет красивой гостьи случается раз в несколько десятков лет, а увидеть эту же комету за свою жизнь мало кому удается. Но почему некоторые кометы возвращаются спустя сотни лет, а некоторые и вовсе «машут рукой» лишь однажды? Дело в том, что большинство комет имеют очень узкие и длинные эллиптические орбиты. Период обращения на них может достигать тысяч лет. А некоторые и вовсе двигаются по гиперболическим орбитам, то есть пролетают нашу Солнечную систему лишь однажды.

Оптические свойства

Конические сечения примечательны своими оптическими свойствами, какими-то интересными закономерностями в поведении лучей, отразившихся от сечения. У каждого из них они свои. Давайте вспомним, что существует закон отражения: угол падения луча равен углу отражения. Подробнее о нем мы говорим в статье «Законы распространения света». Теперь эти свойства станут для нас яснее.

• Лучи, выпущенные из одного фокуса и отразившиеся от эллипса, попадут в другой фокус. То же свойство распространяется и на окружность – любой луч из центра отразится в центр. 

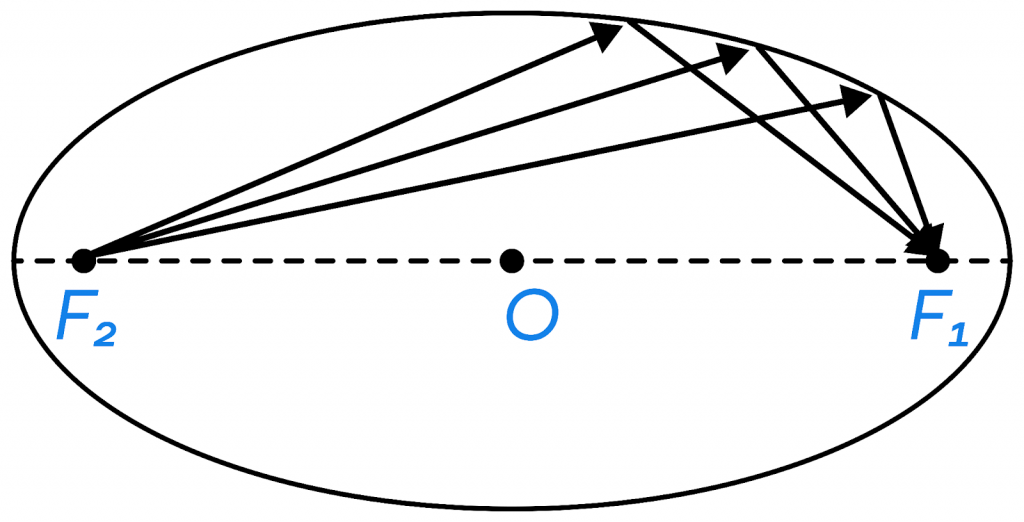
• Параллельный пучок лучей, отразившись от параболы, соберется в фокусе. 

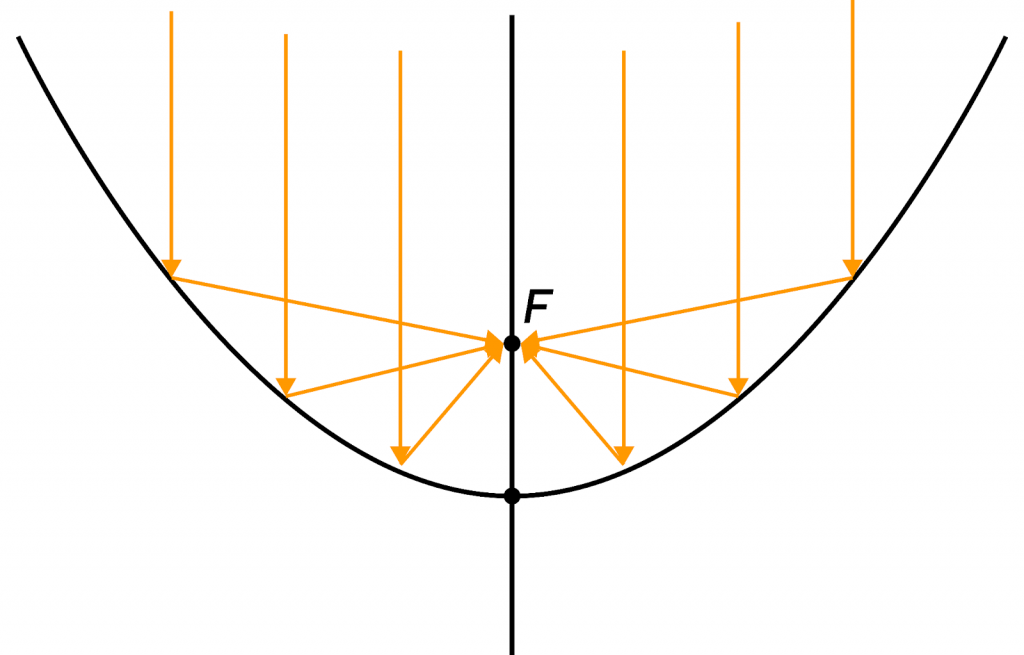
• Луч, выпущенный из фокуса гиперболы, отразится так, что его продолжение попадёт в другой фокус. 

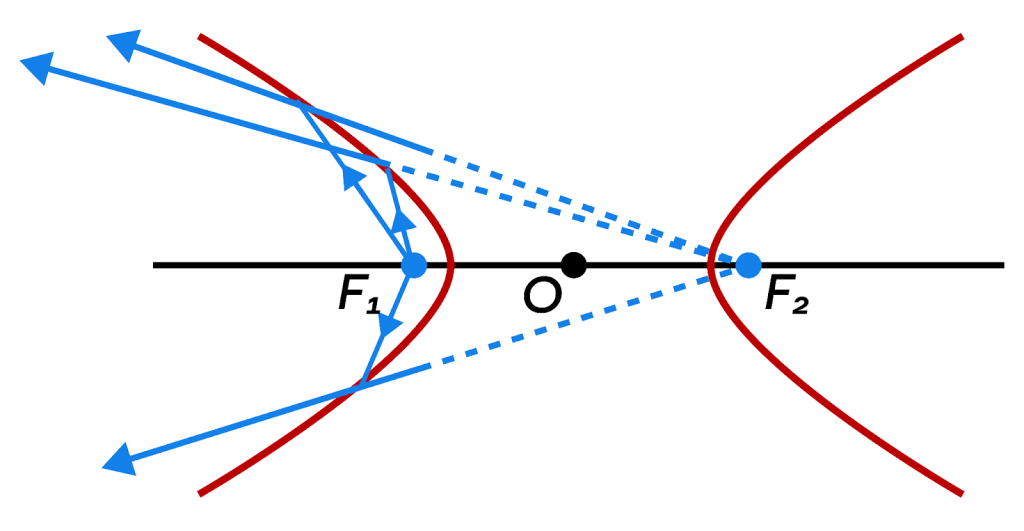
На основе этих свойств работают многие устройства, которыми мы пользуемся каждый день.

Как часто нам помогает парабола в жизни?  Вы никогда не задумывались, почему спутниковая тарелка имеет форму именно тарелки? На самом деле это не тарелка, а парабола, и все благодаря ее оптическому свойству. Что вообще делает спутниковая тарелка? Главная ее задача – принять радиосигнал со спутника и передать его в ваш телевизор. Радиосигнал представляет собой поток параллельных электромагнитных волн. Тарелка поворачивается в сторону этого потока, волны отражаются от стенок устройства и попадают в фокус. В фокусе тарелки установлен приемник, который собирает радиосигнал и отправляет его дальше по проводу в наш телевизор. Если бы не параболическая форма спутниковой тарелки и ее оптическое свойство, такое было бы невозможно. Такая вот магия.

Теперь мы готовы в полной мере погрузиться в изучение законов Кеплера.

Первый закон Кеплера

Первый закон Кеплера звучит следующим образом.

Каждая планета Солнечной системы движется по эллипсу, в одном из фокусов которого находится Солнце.

Этот закон был открыт экспериментально на основе таблиц Тихо Браге, однако его аккуратное физическое доказательство занимает не один лист бумаги. Он стал фундаментальным для своего времени, но неполным. 

Оказывается, что любое тело, движение которого происходит в поле тяжести другого тела, может двигаться лишь по одному из конических сечений. Так, например, траектория тела, брошенного под углом к горизонту в поле тяготения Земли, про которую мы подробно говорили в статье «Движение под действием силы тяжести», является параболой. 

Это умозаключение нетрудно объяснить. Давайте вспомним, что полная механическая энергия тела складывается из суммы кинетической и потенциальной. Тогда запишем, чему равна полная механическая энергия тела на любой орбите. Она состоит из кинетической энергии движения и потенциальной энергии гравитационного взаимодействия. Подробнее о кинетической и потенциальной энергии мы говорили в статье «Энергия. Закон сохранения энергии. Работа и мощность».

\(E_0 = E_к+ E_п = \frac{mv^2}{2} — \frac{GMm}{r}\)
\(E_0\) — полная механическая энергия.
\(E_к\) — кинетическая энергия.
\(E_п\) — потенциальная энергия.
\(m\) — масса тела.
\(v\) — скорость тела.
\(M\) — масса притягивающего тела.
\(G\) — гравитационная постоянная.

Теперь обратим внимание, что конические сечения можно разделить на замкнутые и незамкнутые. Такие орбиты называются соответственно финитные и инфинитные. 

• На финитных орбитах больший вклад в полную энергию вносит гравитационное взаимодействие, а так как оно входит в сумму со знаком минус, то и полная энергия меньше нуля. Из финитных орбит в нашем распоряжении остаются эллипс и окружность, где последняя является частным случаем первого. 

• На инфинитных наоборот – больший вклад вносит кинетическая энергия движения, которая стремится «вырвать» тело из гравитационного взаимодействия и унести его подальше. Полная механическая энергия на таких орбитах больше нуля. Инфинитной является гиперболическая орбита.

• Переходной орбитой от финитной к инфинитной является парабола, на ней полная энергия равна нулю. К слову, параболические орбиты почти не встречаются в природе, потому что достичь абсолютного нуля энергии и иметь его дольше нескольких секунд невозможно в силу постоянных взаимодействий с другими телами. 

Подытожим:

эллипс и окружность	\(E_0< 0\)
парабола	\(E_0= 0\)
гипербола	\(E_0> 0\)

Нетрудно заметить, что движение планет вокруг Солнца должно быть финитным. Иначе мы бы путешествовали в далеком космосе, а о Солнце остались бы лишь воспоминания наших предков. 

Второй закон Кеплера

Второй закон Кеплера уже позволяет решать нам различные задачи, которые раньше встречались на экзаменах, но теперь, к счастью (или к сожалению), нет.

За равные промежутки времени радиус-вектор планеты заметает одинаковые площади.

Положения тел в начале промежутка времени и в конце на рисунке отмечены цифрами и соответствующими радиус-векторами.

Проще говоря, чем ближе к центральному телу находится объект, тем больше его скорость, и наоборот. Удобно записать этот закон в формульном виде, особенно если мы введем такую величину, как сидерический период обращения.

Сидерический период обращения – период полного облета тела своей орбиты. 

Еще можно вспомнить из геометрии, что площадь эллипса равна произведению числа на большую и малую полуоси. Теперь легко получить формулу для второго закона Кеплера:

\(\frac{\Delta s}{\Delta t} = \frac{\pi ab}{T} = const\)
\(\Delta s\) — заметенная площадь.
\(\Delta t\) — промежуток времени.
\(a\) — большая полуось.
\(b\) — малая полуось.
\(T\) — сидерический период.

Давайте теперь вместе решим задачу. А потом обсудим самый важный закон из всех законов Кеплера.

Задача. За четверть сидерического периода радиус-вектор астероида заметает площадь такую же, как площадь равностороннего треугольника со стороной, равной большой полуоси. Найдите малую полуось орбиты астероида, если большая полуось равна 800 тыс. км. 

Решение.
Запишем второй закон Кеплера:

\(\frac{S}{T} = \frac{\Delta s}{\Delta t}\)
\(S\) — площадь эллипса.
\(T\) — сидерический период.
\(\Delta s\) — площадь, заметенная радиус-вектором.
\(\Delta t\) — промежуток времени.

Пусть a и b – малая и большая полуось эллипса соответственно. Тогда площадь эллипса вычисляется по формуле:
\(S = \pi ab\)

Промежуток времени по условию можно выразить через период как \(\Delta t = \frac{T}{4}\)

Заметенную радиус-вектором площадь по условию придется искать как площадь равностороннего треугольника. Нарисуем его и выразим площадь.

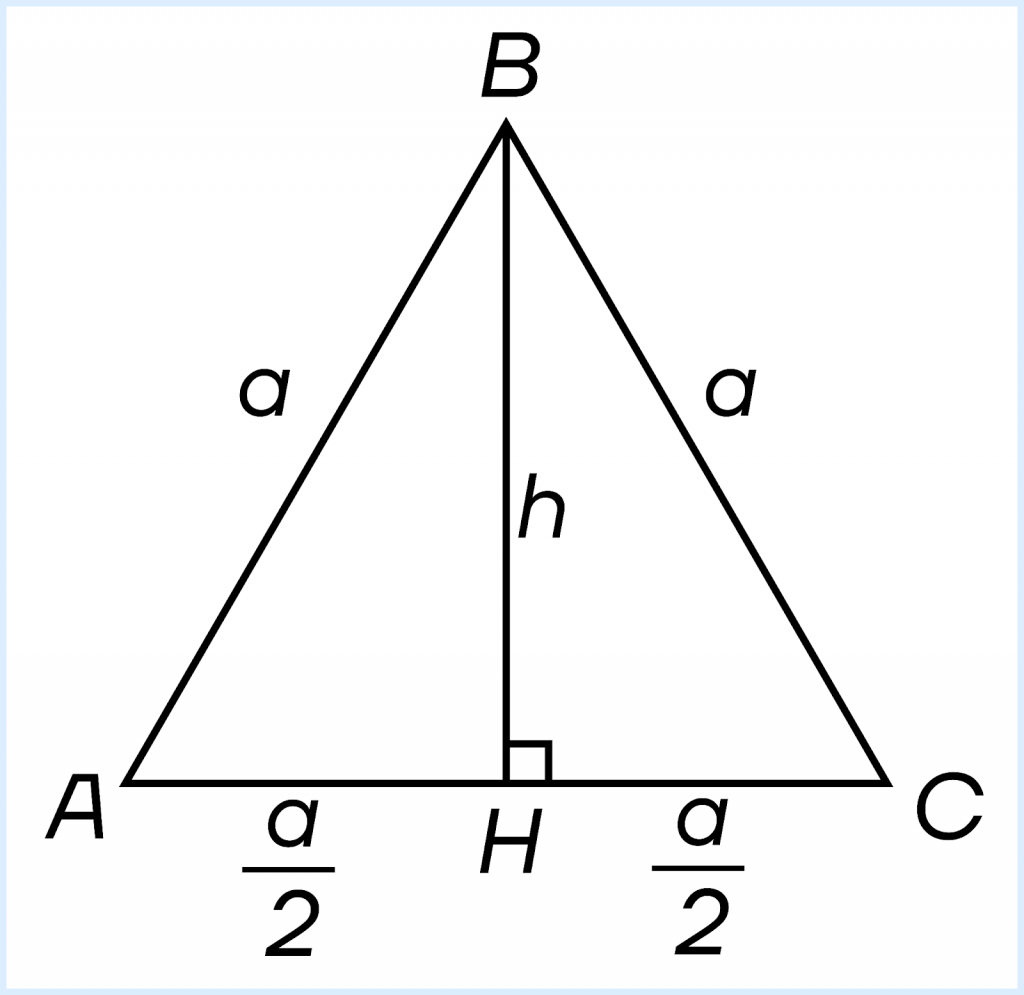
Площадь можно найти как половину произведения стороны на высоту:
\(\Delta s = \frac{1}{2} ah\)

Высоту можно выразить по теореме Пифагора для треугольника ABH:
\(h = BH = \sqrt{AB^2 — AH^2} \sqrt{a^2 — (\frac{a}{2})^2} = \sqrt{\frac{3a^2}{4}} = \frac{\sqrt{3}}{2}a\)

Теперь подставим высоту в выражение для площади: 
\(\Delta s = \frac{1}{2} a \cdot \frac{\sqrt{3}}{2}a = \frac{\sqrt{3}}{4}a^2\)

Мы все нашли, осталось лишь подставить во второй закон Кеплера:
\(\frac{\pi ab}{T} = \frac{\frac{\sqrt{3}}{4}a^2}{\frac{T}{4}}\)

Преобразуем выражение: 
\(\frac{\pi ab}{T} = \frac{\sqrt{3}a^2\cdot4}{4T} = \frac{\sqrt{3}a^2}{T}\)

Сократим на a в числителе и T в знаменателе:
\(\pi b = \sqrt{3}a\)

Выразим b и получим итоговый ответ: 
\(b = \frac{\sqrt{3}a}{\pi} = \frac{1,73 \cdot 800 \cdot 10^3 \cdot 10^3 \text{м}}{3,14} = 4,4 \cdot 10^8\: \text{м} = 441 \:\text {тыс.км}\)

Ответ: 441 тыс. км.

Сколько лет в году? Мы привыкли измерять время в годах. Для нас это 365 дней, и один раз в 4 года – 366 дней. Еще многие знают, что год – это время, за которое Земля делает полный оборот вокруг Солнца. Но ведь Солнце не стоит на месте. Оно также вращается вокруг центра нашей галактики Млечный Путь, где расположена сверхмассивная черная дыра. Тогда почему бы нам не отсчитывать год как время полного оборота солнечной системы вокруг центра галактики? Оказывается, что такой год будет равен 230 миллионам наших Земных лет в силу огромного расстояния между Солнечной системой и центром галактики. Согласитесь, не очень удобно.

Третий закон Кеплера

Самым содержательным является третий закон Кеплера, он позволяет находить сидерический период.

Квадраты сидерических периодов относятся как кубы больших полуосей орбит.

Этот закон позволяет сравнивать сидерические периоды и большие полуоси двух орбит тел, вращающихся вокруг одного центрального тела. В формульном виде это выглядит так.

\(\frac{T_1^2}{T_2^2} = \frac{a_1^3}{a_2^3}\)
\(T_1,T_2\) — сидерические периоды первого и второго тела.
\(a_1,a_2\) — большие полуоси первого и второго тела.

Однако порой становится неудобно сравнивать две орбиты. На помощь приходит 3 закон Кеплера в обобщенном виде.

\(T^2 = \frac{4 \pi^2 a^3}{G(M+m)}\)
\(T\) — сидерический период.
\(a\) — большая полуось.
\(G\) — гравитационная постоянная.
\(M\) — масса притягивающего (центрального) тела.
\(m\) — масса вращающегося тела.

Обратим внимание, что в знаменателе стоит сумма масс лишь в том случае, если массы обоих тел соизмеримы. Например, две звезды, вращающиеся вокруг общего центра масс. Если объектами являются тела, чьи массы сильно отличаются, например, планета и звезда или планета и спутник, то в знаменателе принято писать лишь массу центрального тела, то есть того, чья масса больше. 

Давайте докажем это соотношение для круговой орбиты в том случае, когда массы тел сильно отличаются. Если вы забыли кинематику вращательного движения, на которую мы будем ссылаться далее, советуем прочитать статью «Движение по окружности».

Пусть наше малое тело массой m вращается на круговой орбите вокруг центрального тела массой M. Радиус орбиты R. Запишем второй закон Ньютона для маломассивного тела. 

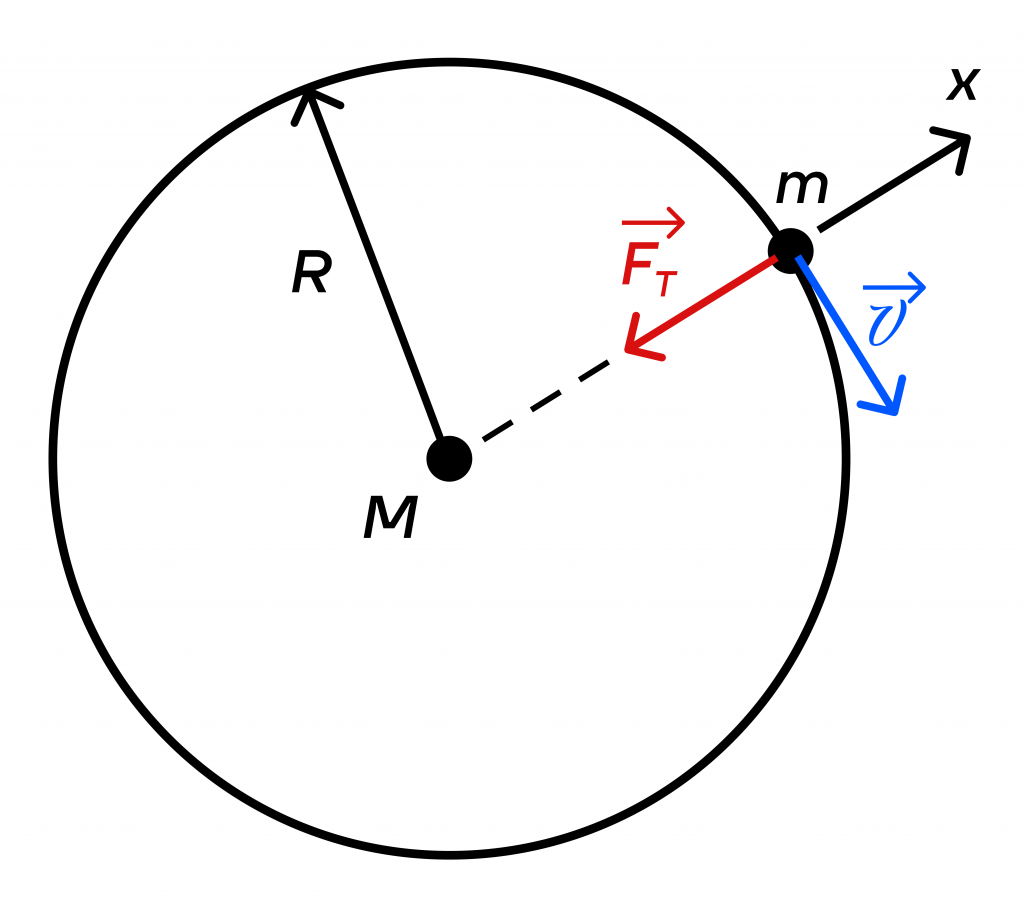
На него действует сила тяготения со стороны центрального тела. 

В векторном виде второй закон Ньютона выглядит так:

\(\vec{F_т} = m \vec{a}\)

Наше тело движется по окружности равномерно, следовательно, оно движется под действием центростремительного ускорения. Тогда:

\(a = a_{\text{ц.с}} = \frac{v^2}{R}\)

Силу тяготения можем расписать по закону Всемирного тяготения, про который мы говорили в статье «Закон всемирного тяготения, сила тяжести», следующим образом:

\(F_{\text{т}} = \frac{GMm}{R^2}\)

Спроецируем наш второй закон Ньютона на ось x, которая проходит по радиусу орбиты, и подставим все формулы.

\(x: \frac{GMm}{R^2} = \frac{mv^2}{R}\)

Сократим на R в знаменателе и на m в числителе. Мы получили выражение для квадрата скорости.

\(v^2 = \frac{GM}{R}\)

Теперь вспомним, что период вращения вычисляется по формуле

\(T = \frac{2 \pi R}{v}\)

Возведем обе части равенства в квадрат и подставим предыдущее выражение

\(T^2 = \frac{4 \pi^2 R^2 \cdot R}{GM} = \frac{4 \pi^2 R^3}{GM}\)

Если вспомнить, что у окружности большая полуось совпадает с радиусом, то мы получим наш третий закон Кеплера. 

Теперь настало время еще раз попрактиковаться.

Задача. Сравните период обращения Луны вокруг Земли с учетом массы Земли и без нее. Сравните найденный период с табличным. Масса Луны равна \(7,35*10^{22}\) кг, масса Земли – \(5,97*10^{24}\) кг. Большая полуось орбиты луны – 384 400 км. Табличный период обращения Луны вокруг Земли – 27,32 суток.

Решение.
Запишем два третьих закона Кеплера, с учетом массы Земли и без:

\(T_1^2 = \frac{4 \pi^2 a^3}{GM}\)
\(T_2^2 = \frac{4 \pi^2 a^3}{G (M + m)}\)
\(T_1\) — период обращения Луны вокруг Земли без учета массы Луны.
\(T_2\) — период обращения Луны вокруг Земли с учетом массы Луны.
\(a\) — большая полуось орбиты Луны.
\(M\) — масса Земли.
\(m\) — масса Луны.

Теперь найдем отношения периодов в обоих случаях: 

\(\frac{T_2}{T_1} = \sqrt{\frac{\frac{4 \pi^2 a^3}{GM}}{\frac{4 \pi^2 a^3}{G (M + m)}}} = \sqrt{\frac{M + m}{M}} = \sqrt{1+\frac{m}{M}} = \sqrt{1 + \frac{7,35 \cdot 10^{22}}{5,97 \cdot 10^{24}}} = 1,006\)

Как мы можем видеть, отличие будет лишь в третьем знаке после запятой, то есть в тысячных.
Теперь найдем период обращения Луны вокруг Земли, воспользовавшись второй записью третьего Закона Кеплера.

\(T = \sqrt{\frac{4 \pi^2 a^3}{G(M+m)}} = \sqrt{\frac{4 \cdot 3{,}14^2 \cdot (384\ 400 \cdot 10^3 \: \text{м})^3}{6{,}67 \cdot 10^{-11} \: \frac{\text{м}^3}{\text{кг} \cdot \text{с}^2} \cdot ( 5{,}97 \cdot 10^{24} \: \text{кг} \: + \: 7 {,} 35 \cdot 10^{22} \: \text{кг})}} = 2.359 \cdot 10^6 \: \text{с} = 27,30 \: \text{суток}\)

Наш ответ почти что является табличным значением. Различие в сотых вызвано тем, что мы не учитываем другие эффекты взаимодействия между Землей Луной, такие как, например, приливные силы. Но нашей точности вполне хватает для решения любых задач.

Ответ: отношение периодов 1,006; наиболее точный период равен 27,30 суток. 

Эта задача позволяет нам заметить, что если масса одного тела больше другого в 100 раз, то нам уже не обязательно учитывать обе массы, достаточно записать третий закон Кеплера с учетом наибольшей массы.

Сегодня мы с вами приоткрыли завесу тайн холодного и мрачного космоса: познакомились с великими учеными своего времени, узнали фундаментальные законы движения тел в поле силы тяжести и научились решать важный класс задач. Если вы хотите еще больше погрузиться в глубины физики и узнать для себя очень много нового, обязательно прочитайте статью: «Импульс. Закон сохранения импульса». 

Термины

Асимптота – прямая, к которой стремится кривая, но никогда ее не пересекает. 

Период обращения – величина, равная времени одного оборота по замкнутой траектории.

Поле тяжести – особая форма материи, описывающая гравитационные взаимодействия тел.

Радиус – отрезок, который соединяет центр окружности и любую точку на самой окружности.

Радиус-вектор – вектор, соединяющий начало отсчета и тело.

Траектория – воображаемая линия, вдоль которой движется тело. 

Центр-масс – геометрическая точка, обладающая массой системы. 

Электромагнитная волна – волна, распространяющаяся в электромагнитном поле и несущая энергию. 

Фактчек

• Любое движение тела в поле тяготения можно описать с помощью трех законов Кеплера.
• Любое тело в поле тяжести движется по одному из конических сечений: эллипсу, параболе или гиперболе.
• Конические сечения определяются эксцентриситетом, мерой замкнутости кривой. Эксцентриситет прямой равен бесконечности.
• Каждое коническое сечение, кроме прямой, имеет оптическое свойство, связанное с отражением лучей света в фокус.
• Первый закон Кеплера гласит, что все планеты движутся вокруг Солнца по эллиптическим орбитам. 
• Второй закон Кеплера гласит, что радиус-вектор тела на орбите заметает одинаковые площади за одинаковые промежутки времени.
• Третий закон Кеплера гласит, что отношение квадратов сидерических периодов тел вокруг одного центрального тела равно отношению кубов их больших полуосей. 

Проверь себя

Задание 1.
Чем определяется коническое сечение?

1. видом
2. большой полуосью
3. эксцентриситетом
4. периодом

Задание 2.
Какую площадь заметает радиус-вектор тела за время, равное периоду обращения? 

1. площадь эллипса
2. невозможно посчитать
3. зависит от задачи
4. равную периоду обращения

Задание 3.
Чему равен эксцентриситет прямой? 

1. нулю
2. единице
3. бесконечности
4. не определен

Задание 4.
Как относятся квадраты сидерических периодов вращения тел?

1. как площади
2. как кубы больших полуосей
3. как кубы малых полуосей 
4. как кубы эксцентриситетов орбит

Ответы:1. — 3; 2. — 1; 3. — 3; 4. — 2.