Применение законов Ньютона

На этой странице вы узнаете

• Как связаны законы Ньютона и автобус?
• Трудно ли быть гением?
• Какой логотип был у первых компьютеров фирмы Apple?

Почему мы не можем резко остановиться после быстрого бега или выпрыгнуть на берег из лодки, находящейся в воде? Всему виной законы Ньютона: второй и третий соответственно. О них мы подробно говорили в этой статье. А вот если мы упадем после прыжка или резкого торможения и останемся лежать неподвижно — это будет примером первого закона. 

Решение задач с использованием законов Ньютона

Освежим наши знания и вспомним сами законы:

1. Первый закон Ньютона. Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют никакие посторонние силы.

2. Второй закон Ньютона. Равнодействующая всех сил, действующих на тело, равна произведению массы тела на ускорение:  \(\vec{F}=\vec{ma}\).

3. Третий закон Ньютона. Тела действуют друг на друга с силой, равной по модулю, но противоположной по направлению:  \(\vec{F_1}=\vec{-F_2}\). 

Эти, не побоимся этого слова, знаменитые законы применяются не только для решения задач, но и окружают нас в жизни. Когда вы играете в мяч, толкаете тележку в супермаркете, плаваете в бассейне и даже когда просто лежите на кровати — во всех этих действиях проявляется тот или иной закон Ньютона.

Как связаны законы Ньютона и автобус? Замечали, что, когда мы едем в автобусе, и он резко тормозит, какая-то неведомая сила толкает нас вперед? Так вот, все из-за того, что на нас начинает действовать некоторая сила инерции, которая определяется по второму закону Ньютона: \(\vec{F}=\vec{-ma}\) Когда автобус тормозит, его ускорение направлено в противоположную движению сторону (назад), а значит, сила инерции направлена вперед (так как в формуле стоит минус). Так что не такая уж это неведомая сила! Но не переживайте, еще одну формулу учить не придется. В экзаменационных задачах эта сила не встречается, потому что в них мы рассматриваем инерциальные системы отсчета (а сила инерции действует в неинерциальной). Зато теперь вы можете обосновать с точки зрения физики, почему нужно держаться за поручни.

Применение алгоритма

Перед тем, как мы приступим к решению задач, ознакомимся с общим алгоритмом, с помощью которого решается 99% задач по механике: а именно задачи с 1 по 8 первой части и задачи 25, 30 второй части ЕГЭ или задачи 24, 17, 16, 5 ОГЭ. К тому же знание законов Ньютона пригодится в решении комплексных задач на применение нескольких тем. Ниже представлены самые важные шаги для решения заданий, которые нужно использовать в совокупности.

Алгоритм решения задач на динамику

Шаг 1.

Рисунок — важнейшая составляющая решения заданий на законы Ньютона и динамику в целом.

На рисунке мы изображаем схематично ситуацию, которая описывается в условии задачи. Не забываем изобразить тип движения тел: при постоянной скорости — вектор скорости, при равнопеременном движении — вектор ускорения.

Шаг 2.

Силы, представленные в системе. 

С помощью визуального представления действующих на тела сил уже можно продумывать будущие уравнения и законы для решения задач. 

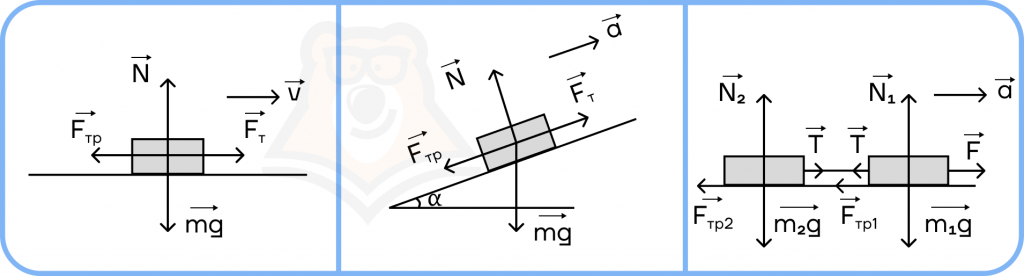
Шаг 3.

Для 2 закона Ньютона: обязательно записываем его в векторном виде, как представлено на рисунке ниже. 

Векторная запись помогает не потерять силы, так как они всегда перед глазами.

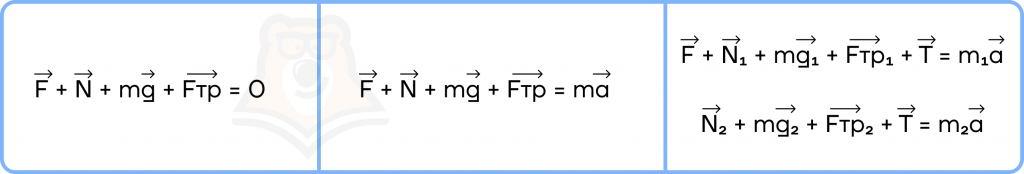
На первом рисунке представлена векторная запись второго закона Ньютона, когда тело двигается равномерно или покоится.

На втором рисунке представлена векторная запись второго закона Ньютона, когда тело двигается равнопеременно (с постоянным ускорением).

На третьем рисунке представлена векторная запись второго закона Ньютона для двух различных тел с разными ускорениями.

Шаг 4.

Выбор направлений координатных осей.

Тоже очень важный этап при решении, так как мы создаем основу для будущих уравнений проекций сил. 
— Для прямолинейного движения обычно выбирают ось х по направлению движения, ось y — перпендикулярно вверх или вниз.
— При движении по наклонной плоскости под углом ɑ: x — по направлению движения вдоль наклонной плоскости, y — перпендикулярно наклонной плоскости.
— Если в системе представлено несколько тел, то для каждого из них вводятся удобные для проецирования оси.

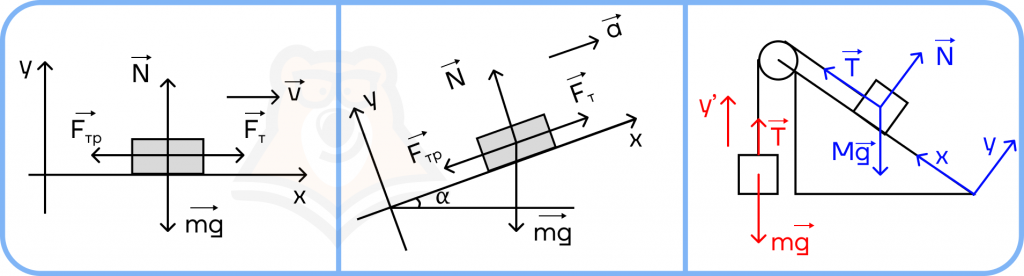
Шаг 5.

Проецирование векторов сил на заданные координатные оси для получения системы уравнений, необходимой для поиска величин, заданных условием задачи.

Шаг 6.

Если в условии задачи упоминается путь и время, то необходимо записать уравнения из кинематики для движения, представленного в задаче, такие как:

\(x=x_0+V_0 t+\frac{at^2}{2}\) — уравнение для координаты при равнопеременном движении.
\(V=V_0 +at\) — уравнение для скорости при равнопеременном движении.

Шаг 7.

Составление системы уравнений и выражение неизвестных величин.

Особенность решения задач с обоснованием 

Для решения задач по сложной механике (№ 30 из КИМа ЕГЭ) есть критерий: верно обоснована возможность использования законов (закономерностей). Критерий гласит о том, что мы должны пояснить, почему в этой задаче можно использовать те или иные законы. Только лишь за обоснование можно получить целый 1 балл!

Если в других задачах достаточно было написать, например, «запишем закон сохранения энергии», то теперь необходимо до этого прописать, почему мы можем применить этот закон. Например, потому что отсутствует трение и сопротивление воздуха. Аналогично с другими законами, еще пример: можно применить закон сохранения импульса, потому что на систему тел не действуют внешние силы.

Представим, что вам попалась нереально сложная задача на динамику. Не приступить к ее решению будет самой большой ошибкой. Обязательно нужно сделать рисунок к задаче и записать второй закон Ньютона. Это уже гарантирует вам 1 балл. А там, глядишь, придет озарение, и вы спокойно сможете решить задачу.

А теперь небольшое лирическое отступление, после которого перейдем к самому серьезному — непосредственно решению задач.

Трудно ли быть гением? Исаак Ньютон по праву может носить это громкое звание — гений! Но далось ему это нелегко. Жизнь ставила много препятствий на его пути ученого начиная с детства. Например, одноклассники недоброжелательно относились к маленькому Исааку. Но он не опустил руки под натиском сверстников. Наоборот — выбился в первые ученики, построив модели ветряных мельниц и солнечных часов. Вот это месть!  Из «лучших побуждений» его близкие однажды сожгли некоторые его рукописи. Они боялись, что Ньютона могут признать еретиком, что повлечет за собой определенные печальные последствия. Вот это «забота»! Но в итоге «награда нашла героя». В 1705 году королева Анна даже посвятила Исаака Ньютона в рыцари за его вклад в науку.

Практика. Применение алгоритма при решении задач

Задача №1.
Угловая скорость вращения небольшого шарика на нити вокруг вертикальной оси равна ω = 10 рад/с. Определите длину нити l, если она отклоняется на угол а = 30 градусов от вертикали.
Какие законы вы использовали для описания движения шарика? Обоснуйте их применение к данному случаю.

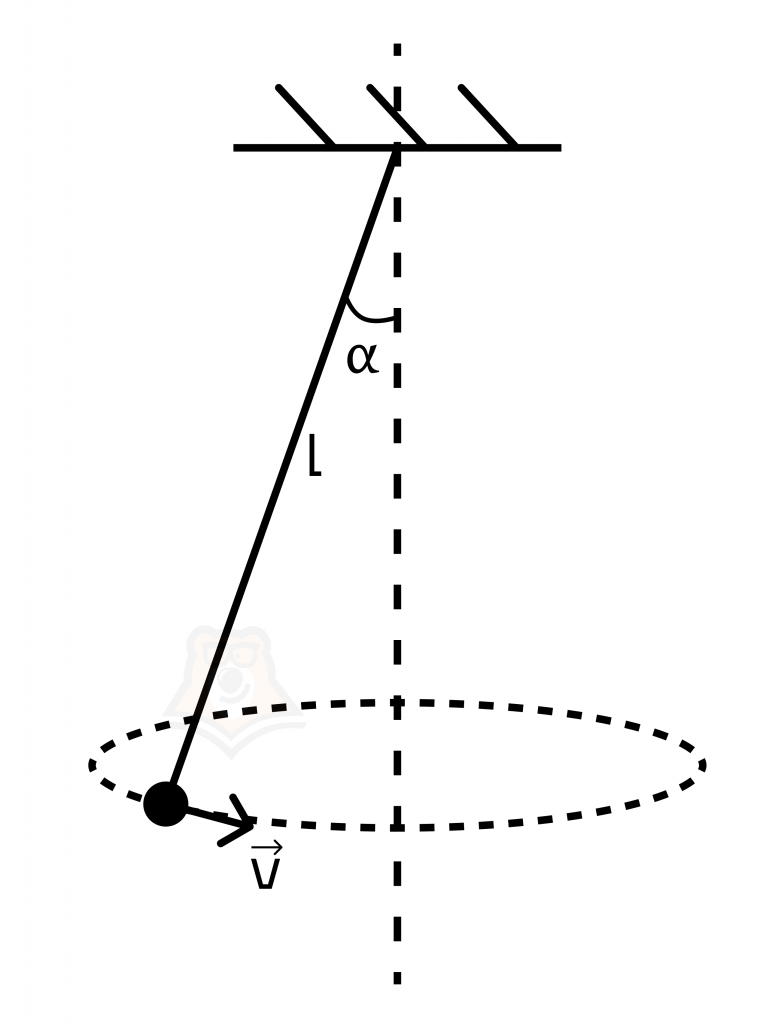
Обоснование: 

Шарик небольшой, его можно принять за материальную точку. Мы приближенно считаем Землю инерциальной системой отсчета, в ней можно записать второй закон Ньютона для шарика. Угол отклонения α не меняется, поэтому траектория шарика — окружность, можно применить законы равномерного движения по окружности.

Решение:

\(w=10\) рад/с \(\alpha=30^{\circ}\)
l= ?

\(\vec{mg}\) — сила тяжести, \(\vec{T}\) — сила натяжения нити, \(\vec{\alpha}\) — центростремительное ускорение шарика при движении по окружности радиуса R.

Введем оси ОХ и ОY, как нам удобно — обычно ось ОХ мы направляем по ускорению, ось ОY перпендикулярно оси ОX. 

Запишем второй закон Ньютона векторно и в проекции на оси:

\(\vec{T}+\vec{mg}=\vec{ma}\).  

В проекции на ось х: \(T\sin{\alpha}=ma (1)\). 

На ось y: \(T\cos{\alpha}-mg=0 ⇔ T\cos{\alpha}=mg (2)\). 

Поделим первое уравнение на второе:  \(\frac{T\sin{\alpha}}{T\cos{\alpha}}=\frac{ma}{mg}⇔ \frac{sin{\alpha}}{cos{\alpha}}=\frac{a}{g}\) .

По формуле для центростремительного ускорения: \(a=\frac{v^2}{R}=w^2 R\), где V — линейная скорость движения шарика. При этом радиус окружности, по которой движется шарик, можно выразить через длину нити и угол: \(R=lsin{\alpha}\).

Совместим имеющиеся формулы: 

\(\frac{sin{\alpha}}{cos{\alpha}}=\frac{a}{g}=\frac{w^2R}{g}=\frac{w^2 lsin{\alpha}}{g}\), \(\frac{1}{cos{\alpha}}=\frac{w^2l}{g}\).

Выразим искомую длину нити:

\(l=\frac{g}{w^2cos{\alpha}}=\frac{10}{10^2*\frac{\sqrt{3}}{2}}≈0,1155 м =11,55 см\).

Ответ: l=11,55 см.

А теперь представим, что вам попалась очень легкая задача, которую вы не раз встречали и решали. В порыве эйфории вы теряете голову и забываете написать слово «ответ». К сожалению, это станет основанием для того, чтобы проверяющий снял вам балл. Поэтому нужно быть очень внимательным и не терять голову.

Задача №2.
Брусок массой М = 400 г соединен с грузом массой m = 600 г невесомой и нерастяжимой нитью, перекинутой через невесомый блок (см. рисунок). Брусок движется по гладкой наклонной плоскости, составляющей угол 30 градусов с горизонтом. Движение происходит без трения. Чему равно ускорение бруска?

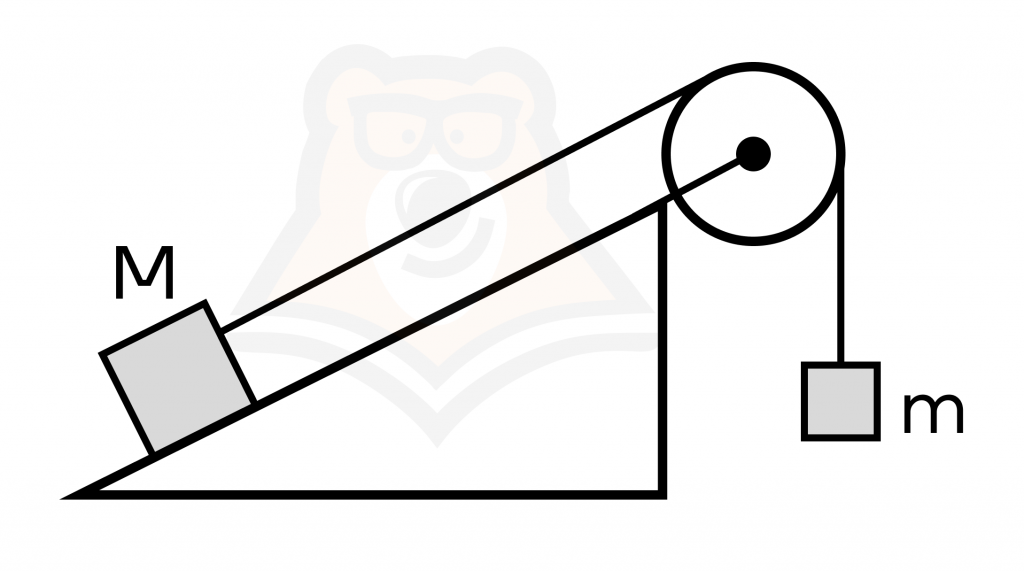
Задача двухбалльная, поэтому обоснование не требуется.

Внимательно прочитаем условие задачи: 

Так как нить невесома и нерастяжима, то из невесомости у нас следует равенство ускорений у двух связанных нитью тел, а из нерастяжимости следует равенство силы натяжения нити по всей ее длине по обе стороны от блока. 

Решение:

M=0,4 кг m=0,6 кг \(\alpha=30^{\circ}\)
a= ?

\(\vec{mg}\) — сила тяжести правого груза, \(\vec{Mg}\) — сила тяжести левого груза, \(\vec{N}\) — сила реакции опоры левого груза, \(\vec{T}\) — сила натяжения нити одинакова для обоих грузов, так как нить невесома и нерастяжима, а блок идеальный, \(\vec{a}\) — ускорение системы.

Запишем второй закон Ньютона векторно и в проекции на оси для левого груза: 

\(\vec{T}+\vec{Mg}+\vec{N}=\vec{Ma}\).  

В проекции на ось х: \(T-Mgsin{\alpha}=Ma (1)\). 

Запишем второй закон Ньютона векторно и в проекции на оси для правого груза: 

\(\vec{T}+\vec{mg}=\vec{ma}\)

В проекции на ось y: \(-T+mg=ma (2)\).

Сложим уравнения (1) и (2):

\(T-Mgsin{\alpha}-T+mg=Ma+ma\)

\((-Msin{\alpha}+m)g=a(M+m) ⇔ a=\frac{(-Msin{\alpha}+m)g}{M+m}=\frac{(-0,40,5+0,6)10}{0,4+0,6}=4\frac{м}{с^2}\).

Ответ: \(a=4\frac{м}{с^2}\).

Задача №3.
Два груза массами \(M_1\)=1 кг и \(M_2\)=3 кг соответственно, лежащие на гладкой поверхности стола, скреплены невесомой и нерастяжимой нитью. На грузы действуют силы \(\vec{F_1}\) и \(\vec{F_2}\). Сила натяжения нити T=14 H. Чему равен модуль силы \(F_1\), если \(F_2\)=20 H?

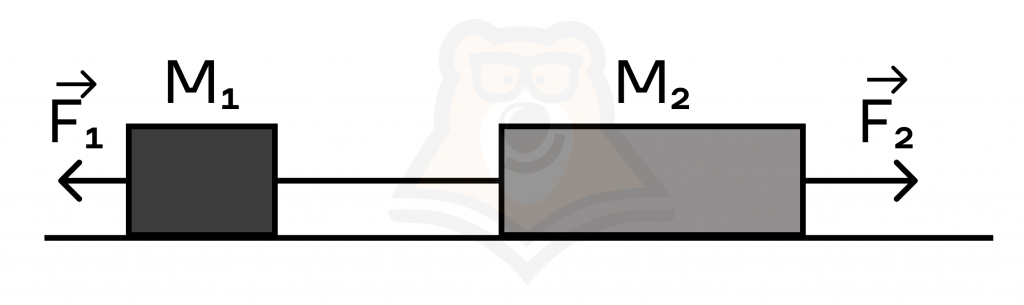
Решение:

\(M_1\)=1 кг \(M_2\)=3 кг \(T\)=14 H \(F_2\)=20 H
a= ?

\(\vec{T}\) — сила натяжения нити, одинаковая для обоих грузов, так как нить невесома, \(\vec{a}\) — ускорение системы.

Запишем второй закон Ньютона проекции на ось х для левого груза:

\(-F_1+T=M_1a (1)\).

Запишем второй закон Ньютона проекции на ось х для правого груза: 

\(F_2-T=M_2a (2)\).

Поделим уравнение (1) на (2):

\(\frac{-F_1+T}{F_2-T}=\frac{M_1a}{M_2a}⇔\frac{-F_1+T}{F_2-T}=\frac{M_1}{M_2}\).

\(-F_1+T=\frac{M_1*(F_2-T)}{M_2} ⇔ F_1=T-\frac{M_1(F_2-T)}{M_2}=14-\frac{1*(20-14)}{3}=12 H\).

Ответ: \(F_1=12 H\).

Задача №4.

Однородный свинцовый шарик, плотность материала которого \(ያ_т=11300\frac{кг}{м^3}\), полностью погружен в воду, опирается на вертикальную стенку и удерживается нитью. Нить образует со стеной угол \(\alpha=30°\). Сила натяжения нити равна T=30 H. Чему равна масса шара, если трения о стену нет?

Решение:

\(ያ_т=11300\frac{кг}{м^3}\) \(T=30 H\) \(\alpha=30°\)
a=?

\(\vec{mg}\) — сила тяжести груза, \(\vec{F_{apx}}\)— сила Архимеда, действующая на шар со стороны воды, \(\vec{N}\) — сила реакции опоры.

Запишем второй закон Ньютона векторно и в проекции на оси: 

\(\vec{T}+\vec{mg}+\vec{F_{apx}}+\vec{N} =0\) (так как система покоится).

В проекции на ось y: \(-Tcos{\alpha}-F_{apx}+mg=0 (1)\). 

Из формулы плотности: объем шара \(V=\frac{m}{ያ_т}\). Тогда по закону Архимеда:

\(F_{арх}=ያ_0gV=ያ_0g\frac{m}{ያ_т}(2)\), 

где \(ያ_0=1000\frac{кг}{м^3}\) — плотность воды. 

Подставим уравнение (2) в (1):

 \(-Tcos{\alpha}-ያ_0g\frac{m}{ያ_т}+mg=0 ⇔ mg(1-\frac{ያ_0}{ያ_т})=Tcos{\alpha}\).
\(m=\frac{Tcos{\alpha}}{g(1-\frac{ያ_0}{ያ_т})}=\frac{30*\frac{\sqrt3}{2}}{10*(1-\frac{1000}{11300})}=2,85 кг\).

Ответ: m=2,85 кг.

Теперь мы с вами умеем решать задачки по механике и применять законы Ньютона в действии. Этот навык еще не раз спасет вас на самом экзамене. Ко всему прочему, мы с вами теперь знаем, как законы Ньютона сказываются на процессах и явлениях, происходящих в нашей жизни ежедневно.

На этом наша статья подходит к концу, но напоследок мы хотим предложить вам еще один интересный факт, чтобы вы могли удивить широким кругозором своих друзей и близких. 

Какой логотип был у первых компьютеров фирмы Apple? В далеких 1976—77 гг. в инструкциях к компьютерам фирмы, которая тогда называлась Apple Computer, Inc., использовался логотип, на котором был изображен Исаак Ньютон. Многие знакомы с легендой о том, что уважаемый ученый открыл закон всемирного тяготения именно сидя под яблоней. Вот этот момент и «запечатлен» создателем логотипа. Вероятно, таким образом создатели компании Apple хотели выразить свое уважение и почтить память великого ученого, внесшего огромный вклад в развитие физики и познание окружающего мира.

Фактчек

• Задачи, основанные на использовании законов Ньютона, решаются с помощью единого алгоритма.
• Нужно знать критерии, по которым эксперты будут оценивать работы на экзамене.
• Только лишь за обоснование в задании № 30 из КИМа ЕГЭ можно получить 1 первичный балл.

Проверь себя

Задание 1.
Какой самый первый шаг к решению должен последовать после прочтения условия задачи?

1. Составление уравнения.
2. Обозначение всех сил.
3. Рисунок.
4. Закрыть задачу и больше на нее не смотреть.

Задание 2.
Если система покоится, то необходимо:

1. Ничего не предпринимать. Решать задачу в привычном виде.
2. Перейти к кинематике.
3. Написать обоснование, почему тело покоится.
4. Приравнять к нулю ускорение.

Задание 3.
За что могут снять 1 балл проверяющие ЕГЭ?

1. За отсутствие второго закона Ньютона в векторном виде.
2. За отсутствие ответа.
3. За неправильные математические расчеты.
4. За все вышеперечисленное.

Задание 4.
В чем особенность оценки задачи №30?

1. Нужно написать ответ.
2. Нужно начертить рисунок.
3. Решение должно быть шаблонным.
4. Нужно пояснять, почему мы можем использовать физические законы.

Ответы: 1. —  3; 2. — 4; 3. — 4; 4. — 4.