Основы графов. Алгоритм Дейкстры

На этой странице вы узнаете

• Как уехать в Париж навсегда?
• Что общего у информатиков и биологов?
• Как Дейкстра облегчил нашу жизнь?

У навигаторов тяжелая работа. Дорог много — какие-то длиннее, на других пробки или одностороннее движение. Попробуй-ка разобраться с этим объемом данных, да ещё и пользователям постоянно что-то нужно… Давайте посмотрим, с чем конкретно приходится работать навигаторам.

Понятие графов

Сегодня речь пойдет о графах, но не тех, которые жили в Европе в Средневековье, а чуть более современных. Хотя и те графы-дворяне, и наши, из информатики, порой отправляются в путешествия. А что же мы? Пожалуй, присоединимся. 

Для начала познакомимся с основными терминами.

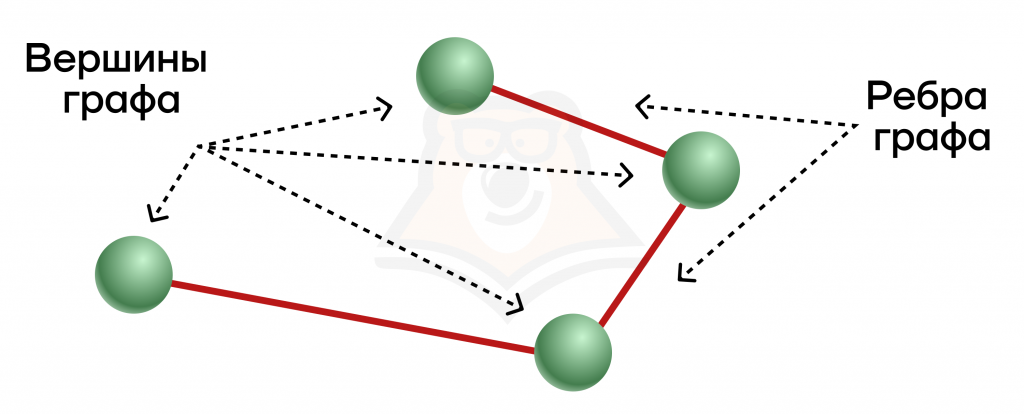
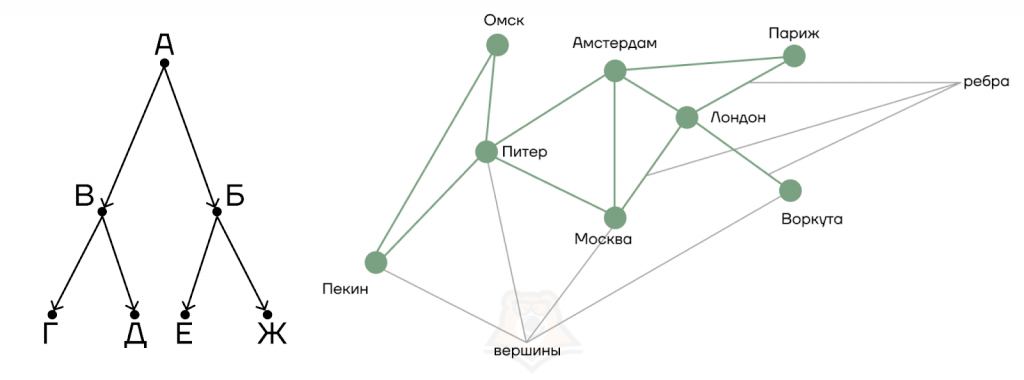
Граф — это совокупность вершин, часть из которых соединена ребрами.

Проще всего представить себе граф, как этакий поломанный многоугольник из геометрии. Часть его точек (вершин) соединены линиями (ребрами), но некоторая часть отрезков потерялась.

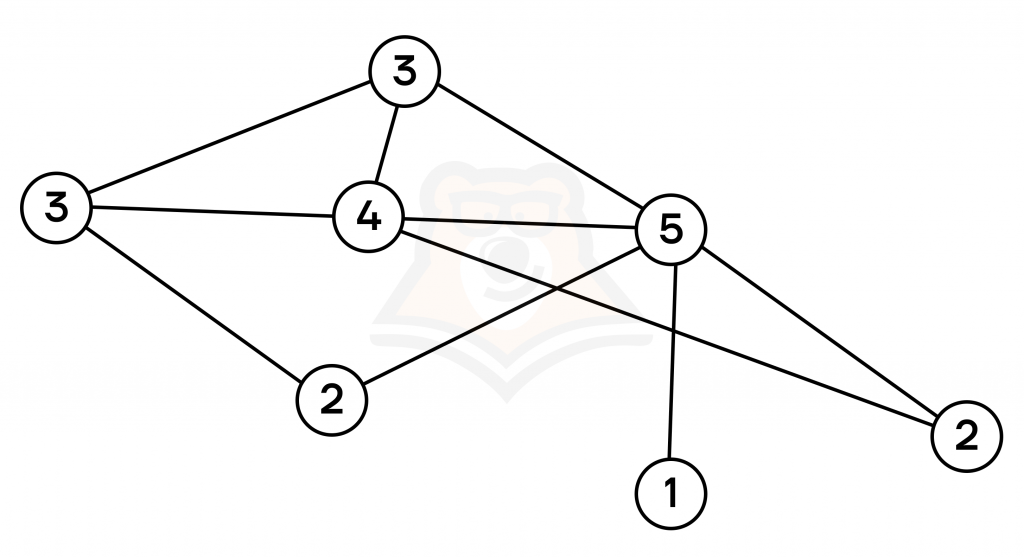
Степень вершины — это количество ребер, входящих и выходящих из вершины.

На рисунке ниже показана степень каждой вершины:

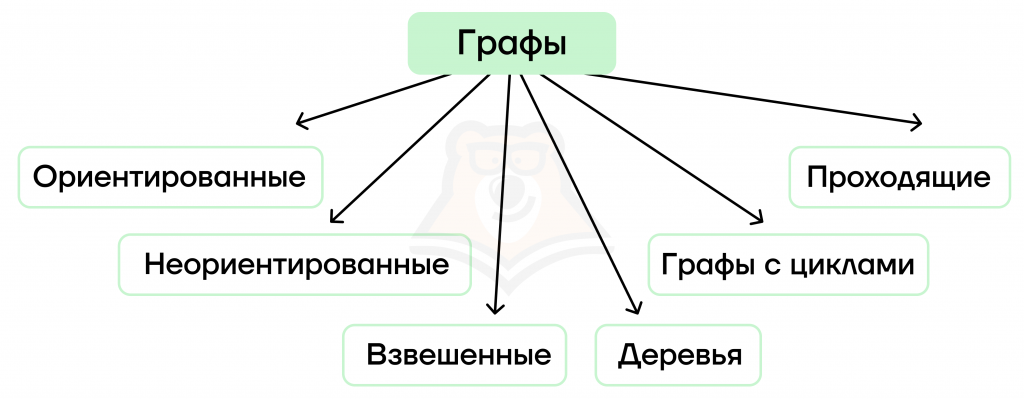
Виды графов

Чтобы лучше разобраться с графами, рассмотрим, какими они бывают:

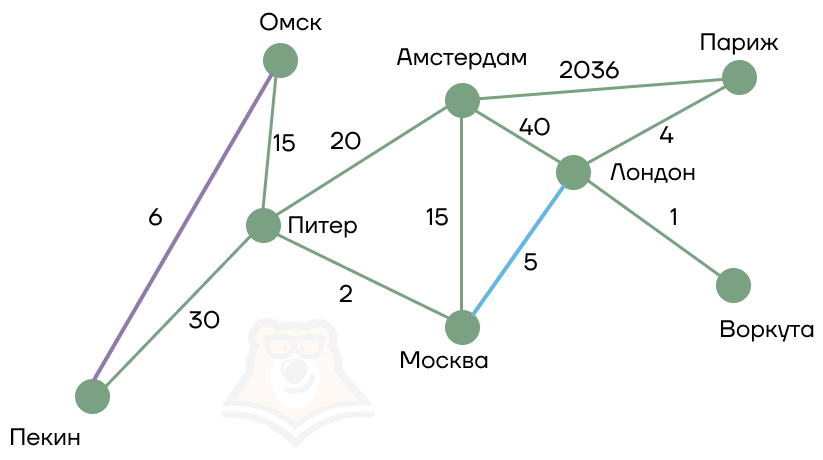
1. Граф можно сравнить с картой страны, в которой вершинами являются отдельные города, а ребрами — дороги. В любом графе перемещаться можно только по ребрам. Так, в примере ниже напрямую из Пекина можно добраться в Омск, а вот в Москву — только через Питер.

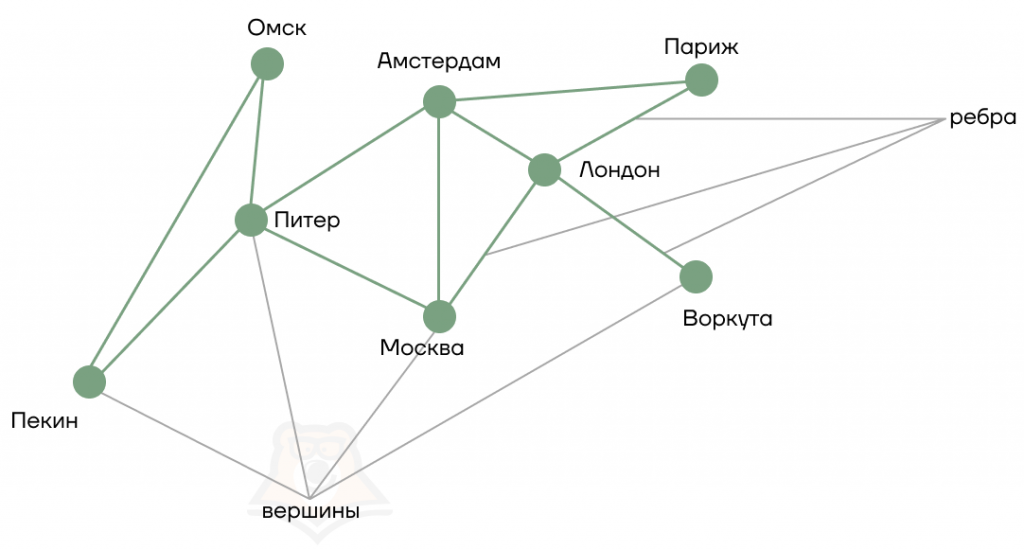
Это пример неориентированного графа. В таком графе по каждому ребру можно двигаться в любую сторону, например, нам открыты обе дороги: и Лондон — Воркута, и Воркута — Лондон.

Такие графы также называются двунаправленными, так как их ребра связывают две вершины, между которыми можно передвигаться в обе стороны.

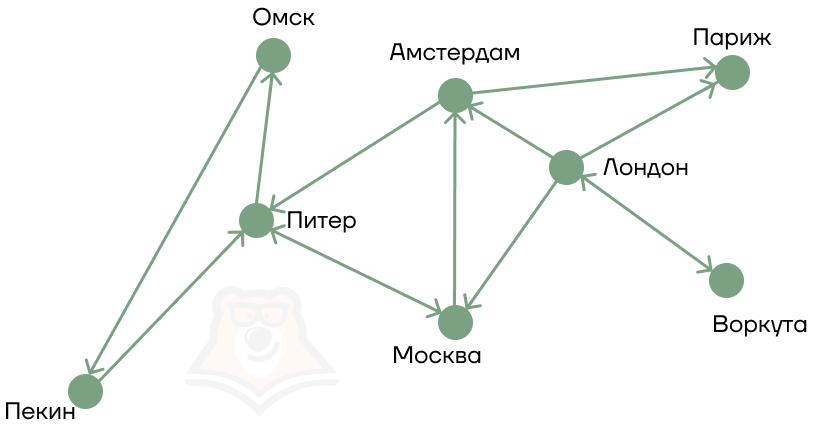
2. Но бывают случаи, когда по дороге можно двигаться только в одну сторону. В ориентированном графе ребра получают свое направление, по которому и происходит движение. 

Это можно сравнить с дорогами с односторонним движением: по такой дороге можно легко попасть из точки А в точку Б, но вернуться тем же путем не получится.

Как уехать в Париж навсегда? В ориентированных графах бывают тупиковые пункты, то есть те пункты, из которых нельзя перейти в другие. Так, в примере ниже Париж оказывается тупиком. В него можно попасть и из Амстердама, и из Лондона, но оба эти ребра — билеты в один конец, так как против направления в ориентированном графе двигаться нельзя. Зато теперь можно бесконечно завтракать круассанами с видом на Эйфелеву башню!

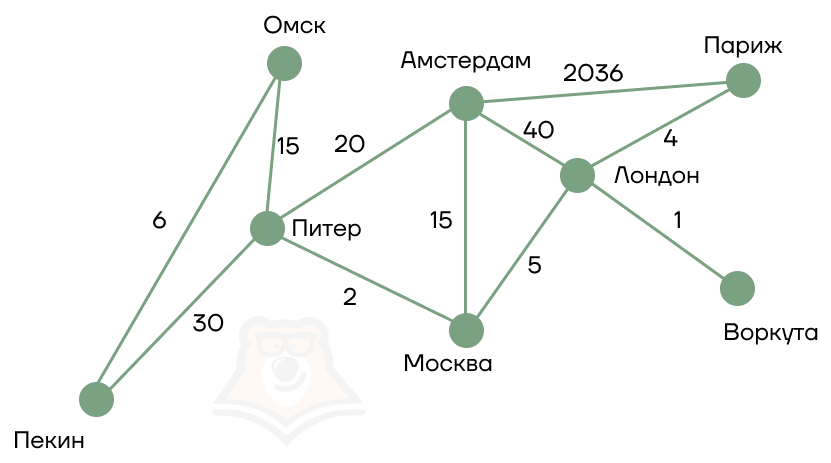
3. У ребер взвешенного графа появляется вес, в данном примере он обозначает «длину» дороги между пунктами. 

В следующем примере:

• прямая дорога Лондон — Воркута равна 1;
• прямая дорога Амстердам — Париж равна 2036;
• путь Пекин — Питер — Москва складывается из весов всех промежуточных ребер и будет равен 30 + 2 = 32.

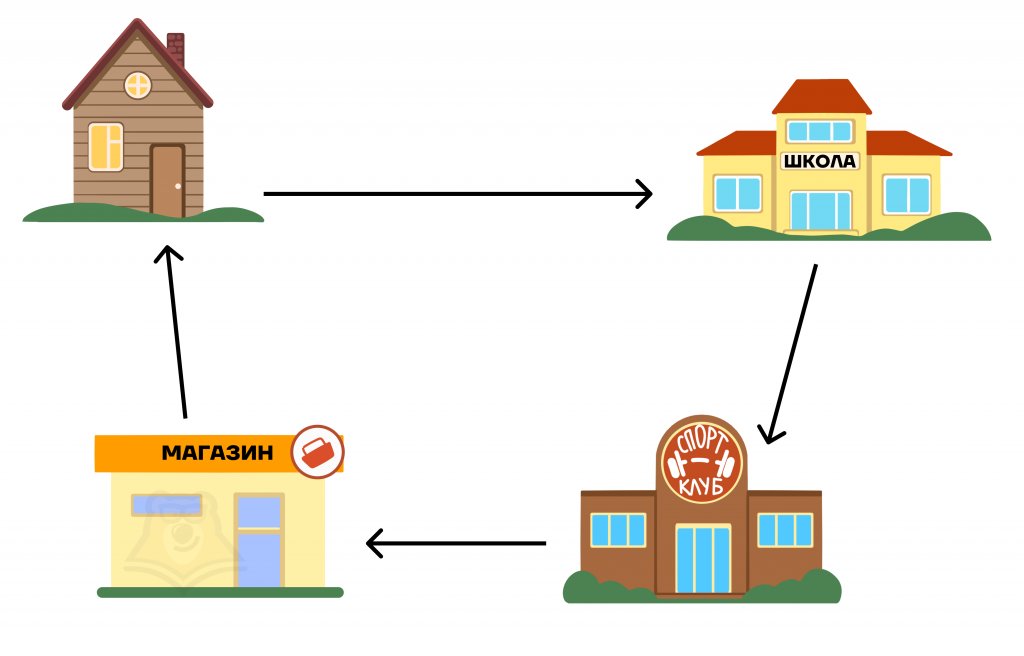
4. Также существуют графы с циклами.

Цикл – это замкнутая цепочка, которая не идет через одну вершину дважды.

Граф с циклом – граф, в котором совпадают начальная и конечная точки.

Данный тип графов можно сравнить с передвижениями в течение дня: утром вы идете из дома в школу, потом на тренировку, в магазин, но вечером вы всегда возвращаетесь домой.

5. Такой граф также будет проходящим.

Проходящий граф — это граф, в котором мы проходим через каждую вершину.

Это значит, что для того, чтобы добраться к конечному пункту, нужно пройти через все пункты. То есть, не сходив в школу, домой вы вернуться не можете!

При решении задач на графы нужно понимать, что такое проходящая и непроходящая траектория. 

Когда в условии задачи просят найти количество дорог из одного пункта в другой, проходящих через какую-нибудь точку, то мы имеем дело с проходящей траекторией. Возвращаясь, к нашим передвижениям в течение дня, представим, что утром перед выходом родители нам говорят, что нужно обязательно сегодня зайти в магазин. В таком случае мы будем строить наши передвижения так, чтобы мы обязательно зашли в магазин.

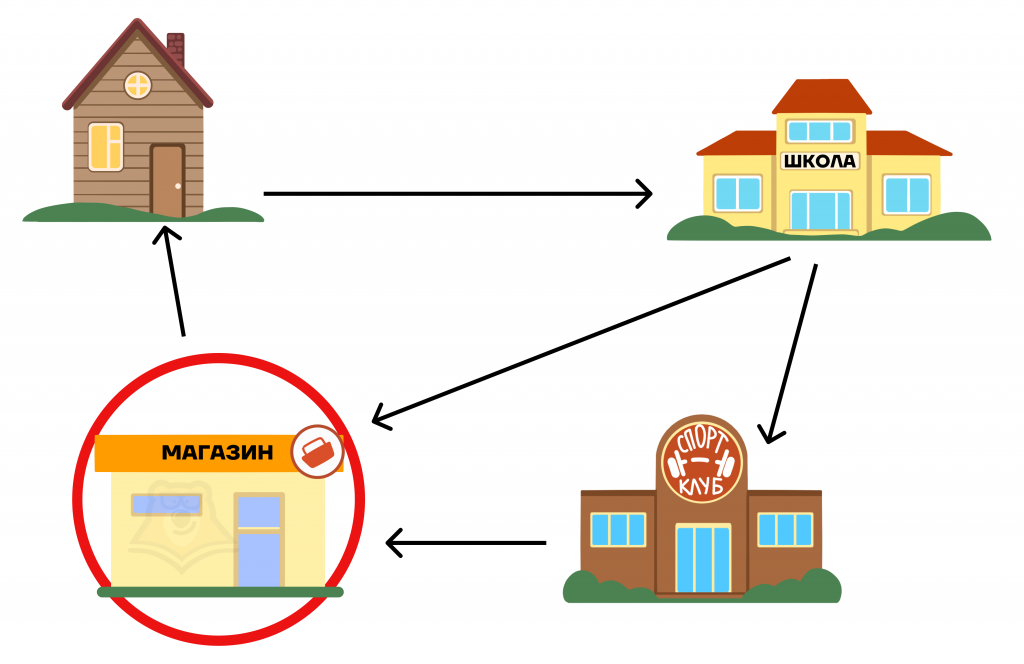
Представим, что сегодня спортивный зал закрыт на ремонт. Тогда все наши передвижения будут строиться так, чтобы не идти на тренировку. Такая траектория будет называться непроходящей.

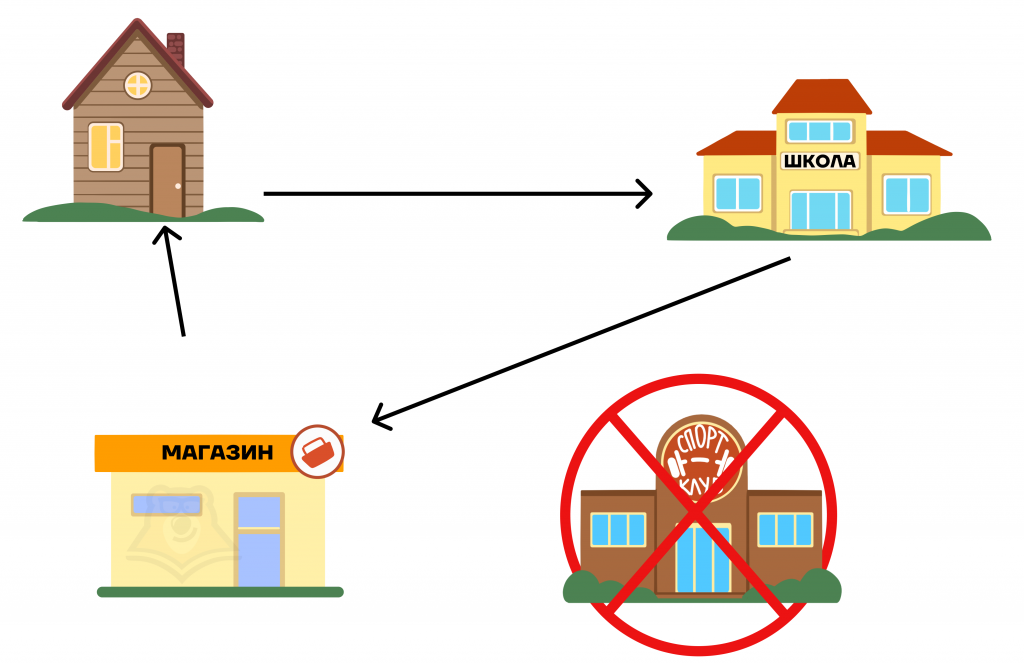
Сейчас мы разобрали все основные виды графов, кроме одного необычного: деревья. Эти графы сильнее всего отличаются от своих «собратьев».

Сейчас мы разберемся, в чем эти отличия.

Понятие дерева

Что общего у информатиков и биологов? Кажется, что эти люди настолько разные, что ничего общего у них быть не может, но на самом деле это не так: и те и другие изучают деревья.

Дерево — это граф, в котором нет циклов. 

Графы такого типа действительно похожи на деревья, правда, перевернутые.

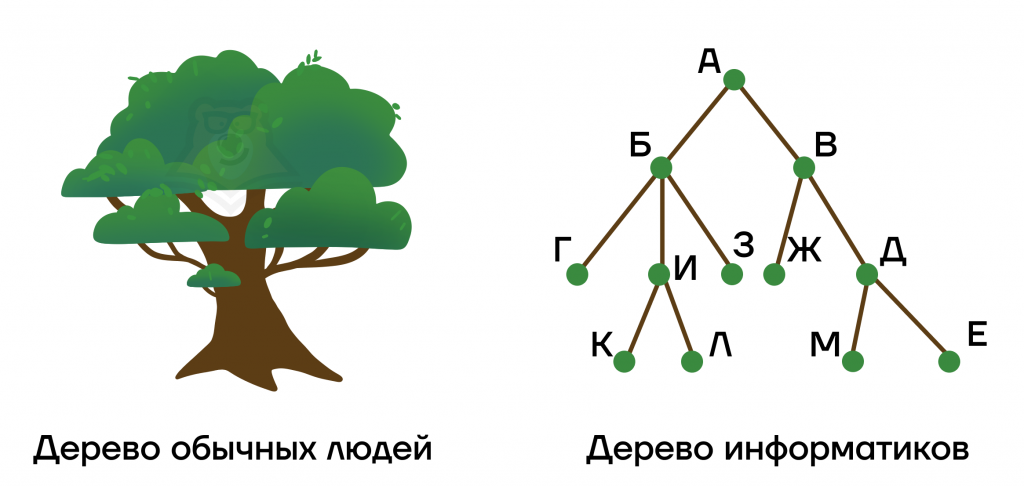
Обычно графы-деревья используют, чтобы разбить задачу на маленькие части или построить генеалогическое древо. 

Рассматривая дерево, нужно обязательно уточнить, что такое истоки и стоки графа.

Понять, как отличить истоки и стоки дерева, нам поможет водопад.

Исток – самая верхняя точка водопада, в нее не попадает вода из других точек, здесь она только стекает вниз.

Истоками называются вершины, в которые не ведет ни одно ребро.

Исток – это начало графа, обычно это самая верхняя точка дерева, из которой далее идут ребра, ведущие к другим вершинам. 

На этом рисунке истоком является вершина А, так как в нее не ведет ни одно ребро.

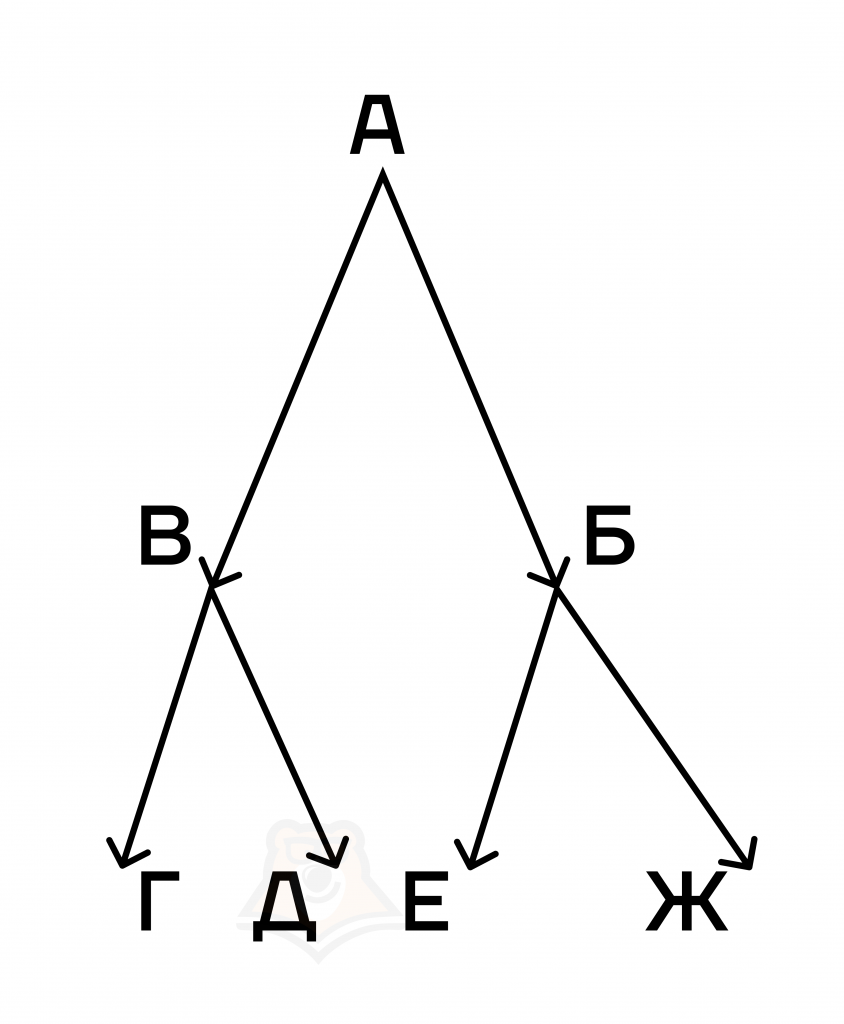
Стоком водопада будет самая его нижняя точка, в нее стекает вся вода, но она больше никуда не уходит.

Самые нижние вершины графа называются стоками.

Стоки — такие вершины графа, в которые входят ребра, но ни одно ребро не выходит. 

На примере выше стоками являются вершины Г, Д, Е, Ж. 

Теперь мы разобрались со всеми видами графов, но, чтобы научиться работать с ними, сначала нужно узнать, какие бывают способы задания графов.

Способы задания графов

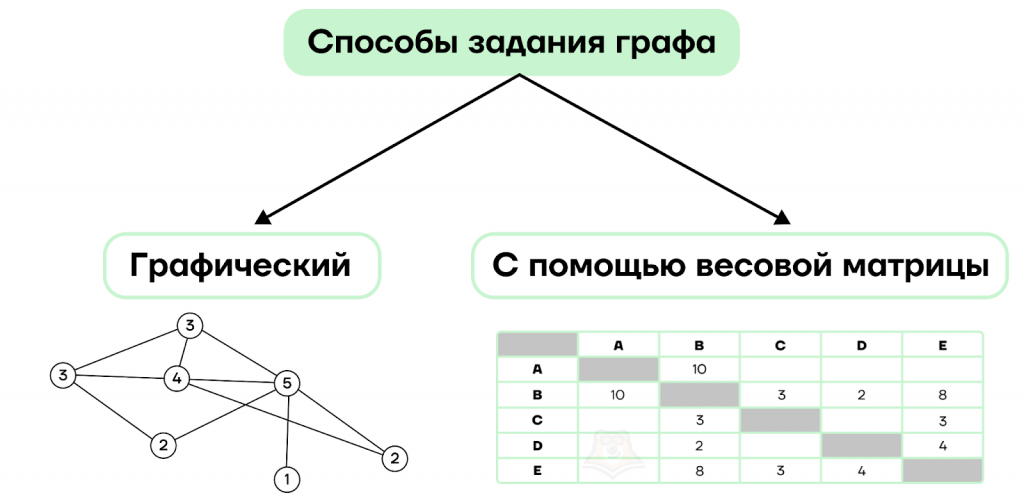
Графы могут задаваться графически или с помощью матрицы.

1. Графический способ задания графа самый распространенный. Он заключается в представлении графа в виде наглядной схемы взаимодействия между вершинами. Выше мы как раз разбирали различные виды графического представления графов. 

2. Теперь разберемся подробнее с матричным методом.

Что такое весовая матрица?

Весовая матрица, или матрица смежности, — еще один способ задания графа. Это таблица, по высоте и ширине которой указаны вершины графа (для удобства — в одинаковом порядке), а в их пересечениях — вес ребра, соединяющего эти вершины. Отсутствие значения в таблице означает, что прямой дороги между пунктами нет.

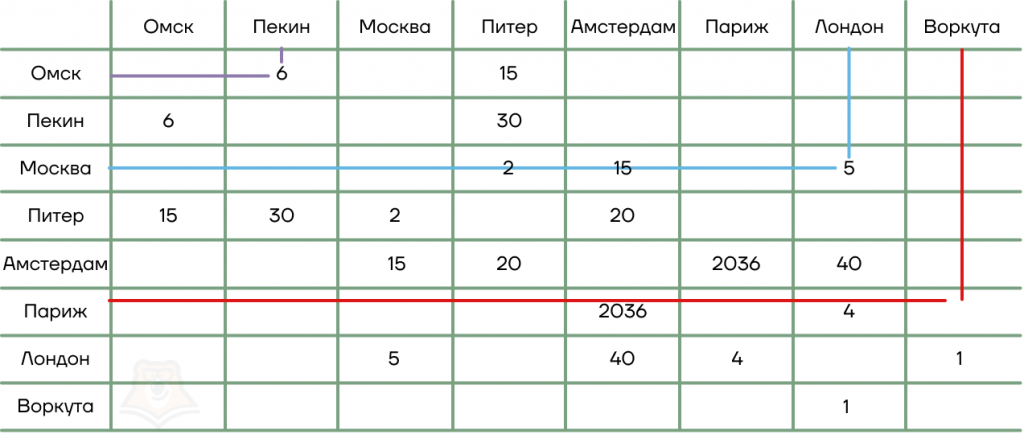
С помощью такой таблицы можно и без графа увидеть, что с чем соединено и сколько будет «весить» дорога. 

В примере:

• На пересечении Омск — Пекин стоит значение 6, значит, вес ребра между ними равен 6.
• На пересечении Москва — Лондон стоит значение 5, значит, вес ребра между ними равен 5.
• На пересечении Париж — Воркута стоит пустое значение, значит, дороги между этими пунктами нет.

Для таблицы выше можно сказать, что она составлена для неориентированного графа, так как значение веса ребра есть у любой пары пунктов — и на пересечении Омск — Пекин, и на пересечении Пекин — Омск. Это можно заметить по тому, что таблица симметрична по диагонали.

Весовую матрицу также можно составить и для ориентированного графа. Тогда симметричными могут остаться только несколько пунктов, ребро между которыми имеет два направления.

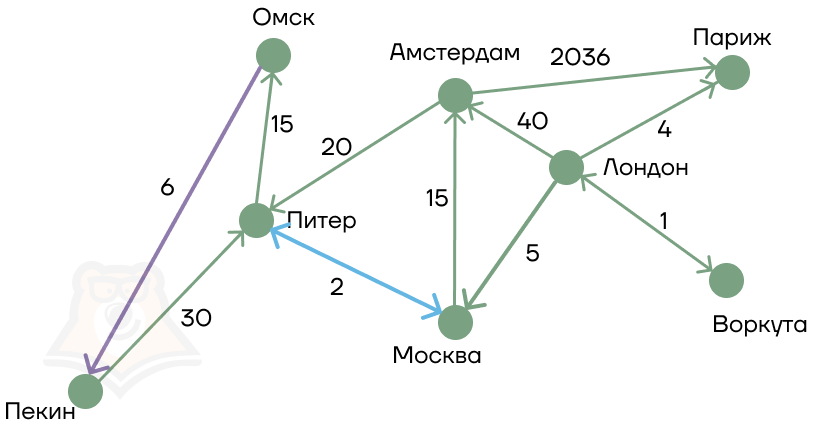
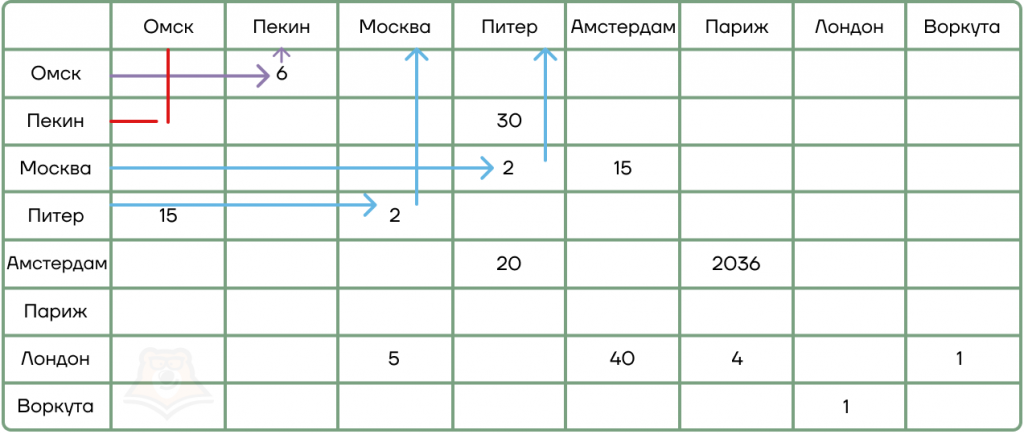
В примере:

• На пересечении Омск — Пекин значение есть, а вот на пересечении Пекин — Омск нет: значит, ребро между этими пунктами имеет направление в сторону Пекина.

Иногда в весовой матрице пишут не длину дорог, а какой-нибудь символ, обычно это «*». Такая матрица означает, что ребра не имеют веса, и она просто показывает наличие дороги из одного пункта в другой.

Итак, подытожим: граф можно задать в графическом виде и с помощью весовой матрицы.

Теперь, когда мы знаем все о графах, можно приступать к решению задач с ними, в этом нам поможет алгоритм Дейкстры.

Алгоритм Дейкстры

Одной из самых интересных тем в работе с графами является алгоритм Дейкстры. Он позволяет намного ускорить решение некоторых задач, поэтому любой уважающий себя информатик должен знать данный алгоритм.

Алгоритм Дейкстры — алгоритм поиска кратчайшего пути из одной вершины графа в другую.

Как Дейкстра облегчил нашу жизнь? Создание алгоритма Дейкстры сделало жизнь любителей информатики намного проще, ведь появился невероятно легкий способ узнать длину кратчайшего пути, не рассматривая множество вариантов по отдельности.

Работу алгоритма можно описать так: из вершины с наименьшей длиной пути мы ищем пути в последующие вершины.

Его реализация происходит следующим образом:

1. Создаем таблицу, в которую будем вписывать значение наименьшего пути до каждой вершины. В самой первой строке для вершины, из которой начинаем движение, ставим значение 0. Для остальных — прочерк.
2. На каждом новом шаге фиксируем наименьшее из всех значений длины пути и рассматриваем все дороги из него (как сумму пути до этой вершины и из нее). Дороги в зафиксированные вершины не рассматриваются.
   
   Для каждой вершины в новой строке записывается одно из двух значений — либо из предыдущей строки, либо новое из рассматриваемой вершины. Выбираем наименьшее значение.

3. Пункт 2 повторяется до тех пор, пока не зафиксируется значение пути до вершины, в которую нам и нужно найти наименьшую дорогу.

Разберем алгоритм Дейкстры на примере и по этой весовой матрице найдем кратчайший путь из пункта А в пункт Е.

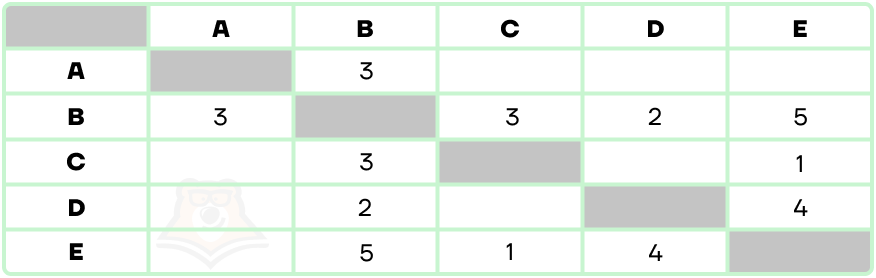
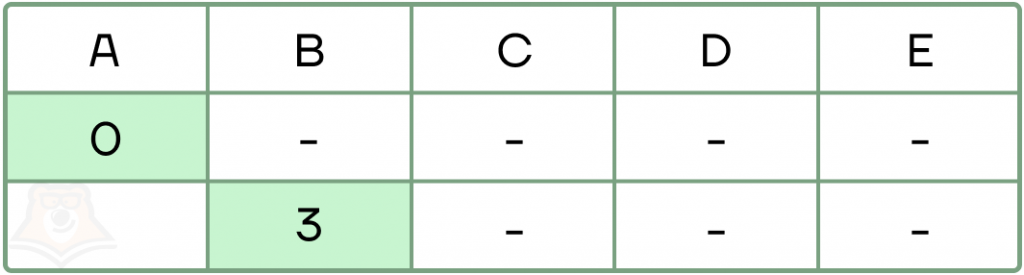
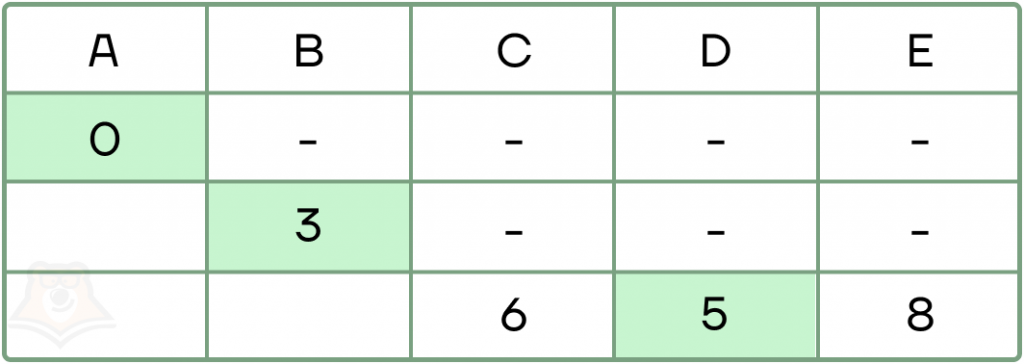
1. Создадим таблицу, в которой будем отмечать длину пути до каждого пункта. Изначально мы стоим в пункте А, ему даем значение 0 и сразу фиксируем. В остальные пути мы еще не добрались, им оставим прочерки.

2. Теперь из начального пункта ищем возможные дороги. Из А можно прийти только в пункт В за 3, помечаем эту длину пути к пункту В и сразу ее фиксируем, так как других у нас пока и нет.

3. Продолжаем следовать алгоритму и теперь идем из пункта В. Из него мы можем прийти в пункты А, С, D и Е. В пункт А нам возвращаться нельзя, его значение мы уже зафиксировали. А вот в другие пути мы еще не попадали, отправимся туда. 

Нужно учитывать, что, например, дорога ВС, равная 3, прибавляется к той, за которую мы дошли до В, так как изначально мы идем из пункта А. Поэтому полный путь в С будет весить 3 + 3 = 6. 

Всем пунктам, куда мы идем из В, даем значение суммы дороги до В и дороги из В. И снова фиксируем наименьшее значение, в данном случае это будет в пункте D.

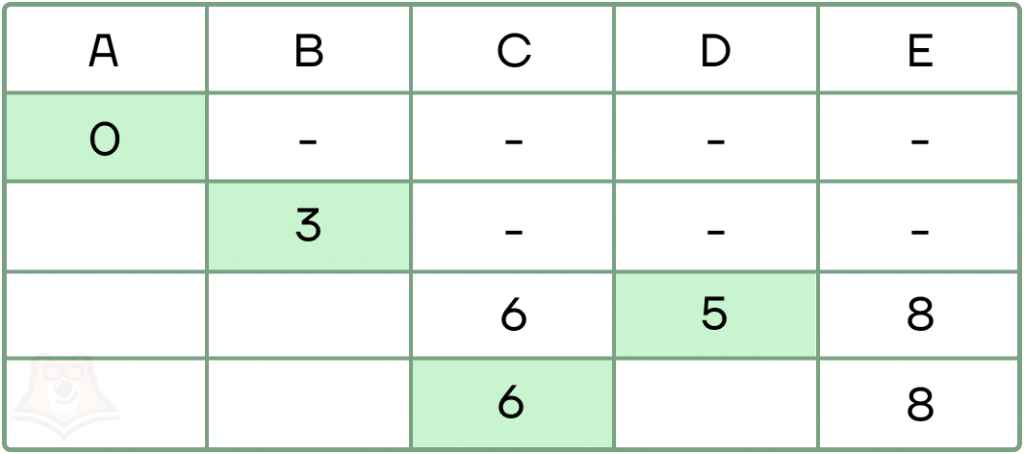
4. Продолжаем движение из зафиксированного пункта D. Из него можно прийти в В, но этот путь нас не интересует, так как путь до В уже зафиксирован. Также из него можно дойти до Е, и вот здесь у нас появляется выбор:

• С одной стороны, мы уже как-то дошли до Е за 8.
• С другой стороны, вместо той дороги мы можем прийти сейчас из пункта D, до которого идти 5, в Е, до которого идти еще 4, итого новая дорога займет 5 + 4 = 9. 

Новая дорога будет длиннее старой, поэтому мы просто не используем ее. Для пункта Е наименьшим вписываем старое значение. 

Также мы еще не рассмотрели пункт С. Его записываем ниже и фиксируем, так как из оставшихся пунктов он будет наименьшим.

5. Последнее, что осталось рассмотреть — пункт С, можно ли из него дойти до Е? Можно, причем дорога СЕ весит 1, тогда полный путь до Е через С будет весить 6 + 1 = 7. Это меньше, чем оставшееся до этого значение 8, поэтому смело его забываем и вписываем новое значение наименьшего пути — 7. 

Все остальные пути уже зафиксированы, новых дорог не будет, мы провели алгоритм до конца, найдя ответ на задачу — 7.

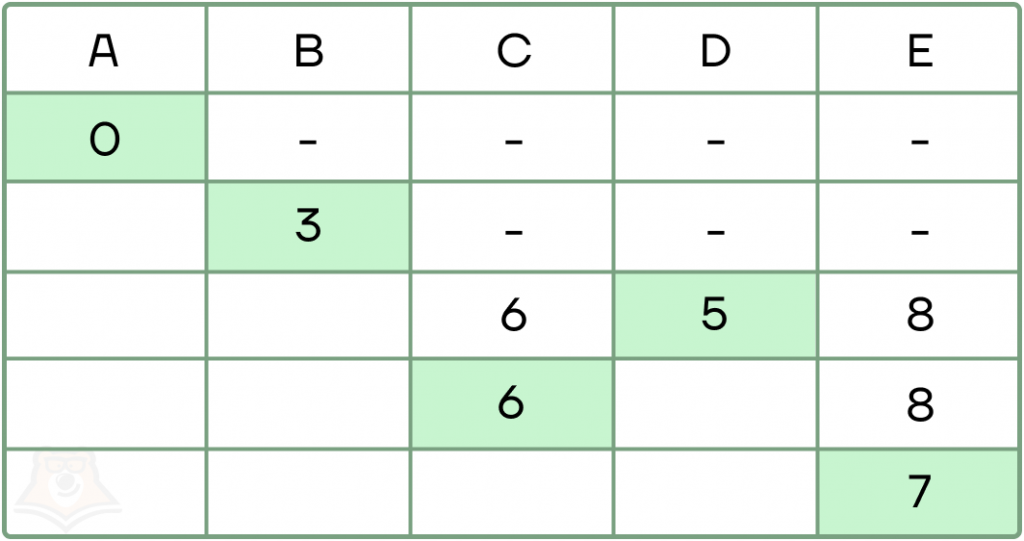
На данном примере отлично видно, что Алгоритм Дейкстры намного облегчил нашу работу, поэтому при решении задач нужно обязательно использовать данный метод. 

Практика

В жизни графы используют для того, чтобы визуально представить сложные системы: планы автомобильных дорог, передвижение самолетов, распределение задач проекта между членами команды. Но также графы — одна из основных тем на ЕГЭ и ОГЭ. Они встречаются в заданиях 4 и 9 ОГЭ, в заданиях 1 и 13 ЕГЭ.

Пример 1. За образец возьмем задачу из номера 9 ОГЭ.

На рисунке дана схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует дорог из города А в город Ж, проходящих через город Г?

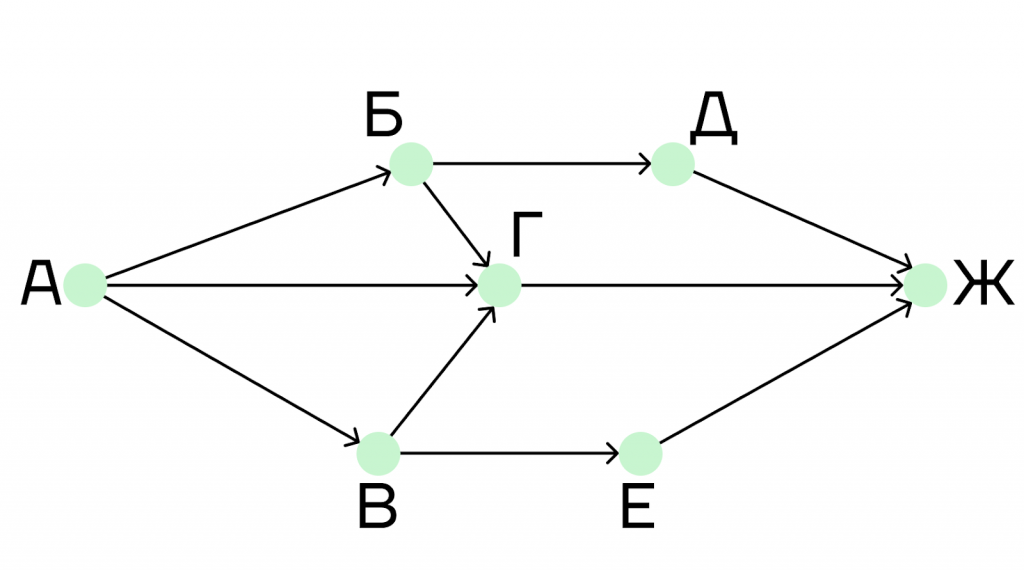
Решение.
В данной задаче дорога из города А в город Ж будет проходящей траекторией, так как в условии сказано, что дорога должна обязательно проходить через город Г.

В задачах такого типа нужно быть очень внимательным к каждой дороге и записывать все найденные величины.

Шаг 1. Мы начинаем наш путь из города А, в него не ведут никакие дороги, поэтому напишем под ним единицу.

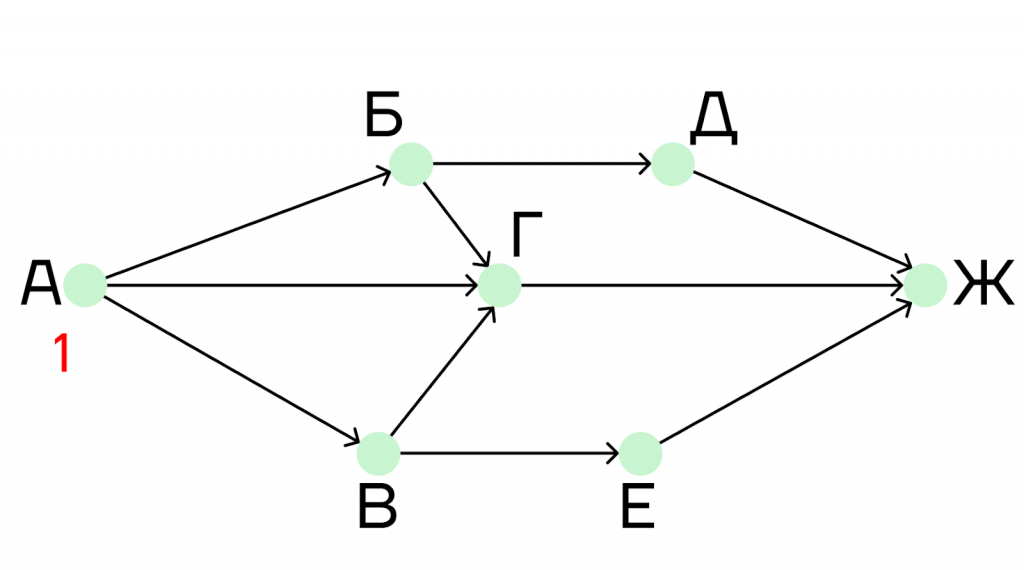
Шаг 2. Рассмотрим пункты Б и В. В оба этих пункта ведет только одна дорога, эта дорога выходит из города А. 

Главное правило таких задач: количество дорог, ведущих в пункт, вычисляется как сумма дорог пунктов, из которых исходят дороги, ведущие в искомый пункт.

В город Б ведет только одна дорога из А, так же как и в город В. Поэтому под этими пунктами напишем единицы.

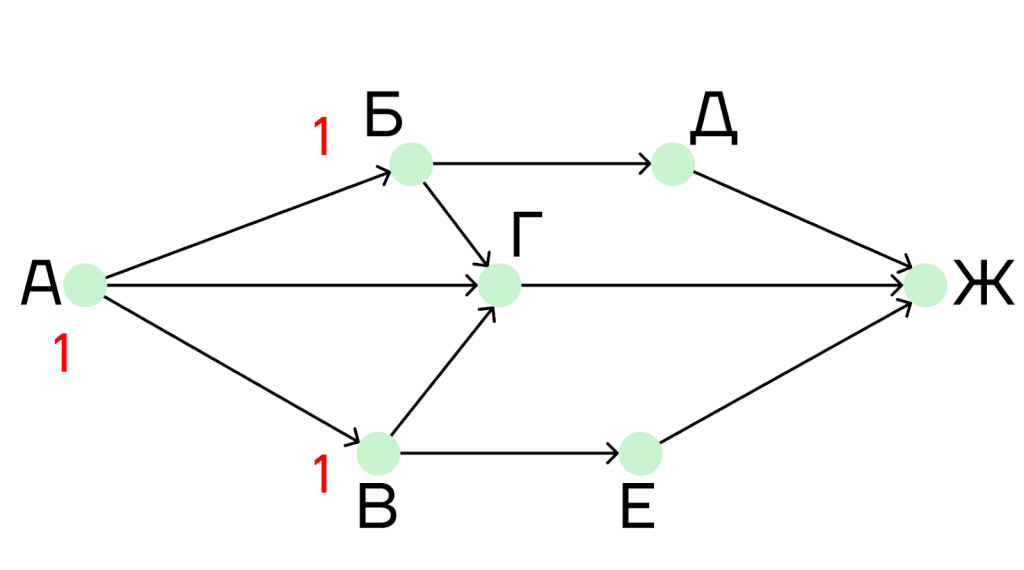
Шаг 3. Теперь рассмотрим пункт Г. Этот пункт для нас очень важен, ведь в условии сказано, что нужно найти количество дорог, проходящих через этот пункт.

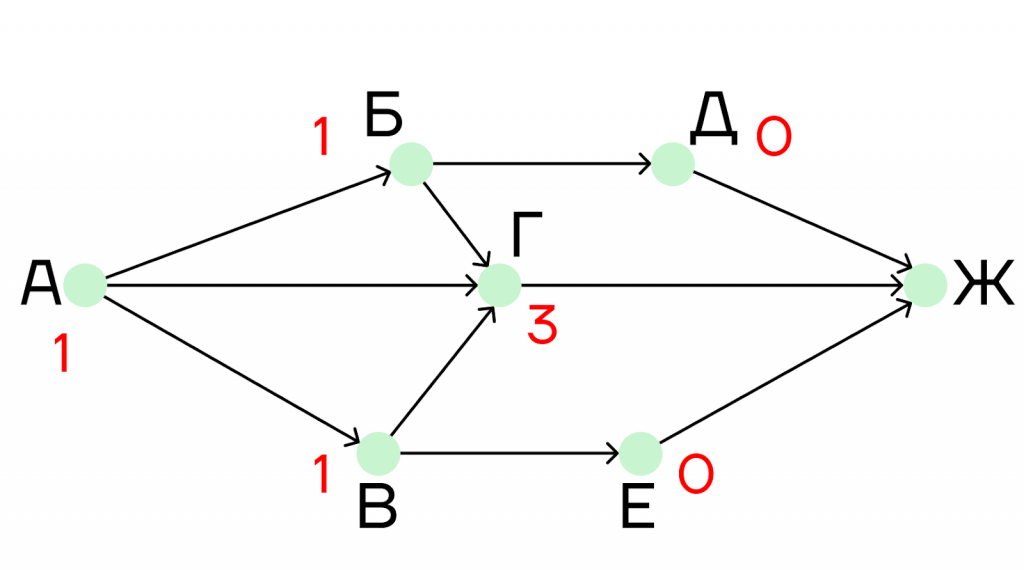
В город Г ведет три дороги: из городов А, Б и В. Следуя правилу из шага 2,  понимаем, что в город Г ведет такое количество дорог, которое равно сумме дорог пунктов, из которых исходят дороги, ведущие в пункт Г. 

В нашем случае это будет: 

1 + 1 + 1 = 3.

Шаг 4. Так как нам нужно найти количество дорог, проходящих через город Г, то пункты, в которые не ведет ни одна дорога из города Г, мы рассматривать не будем. Можно поставить под этими пунктами нули, чтобы они нас не отвлекали.

В нашей задаче такими городами являются Д и Е, поэтому мы их обнулим.

Шаг 5. В пункт Ж ведет три дороги, но две из них исходят из пунктов, которые равны 0. Поэтому считаем только дорогу из города Г.

Итог: из пункта А в пункт Ж идет 3 дороги, проходящие через пункт Г.

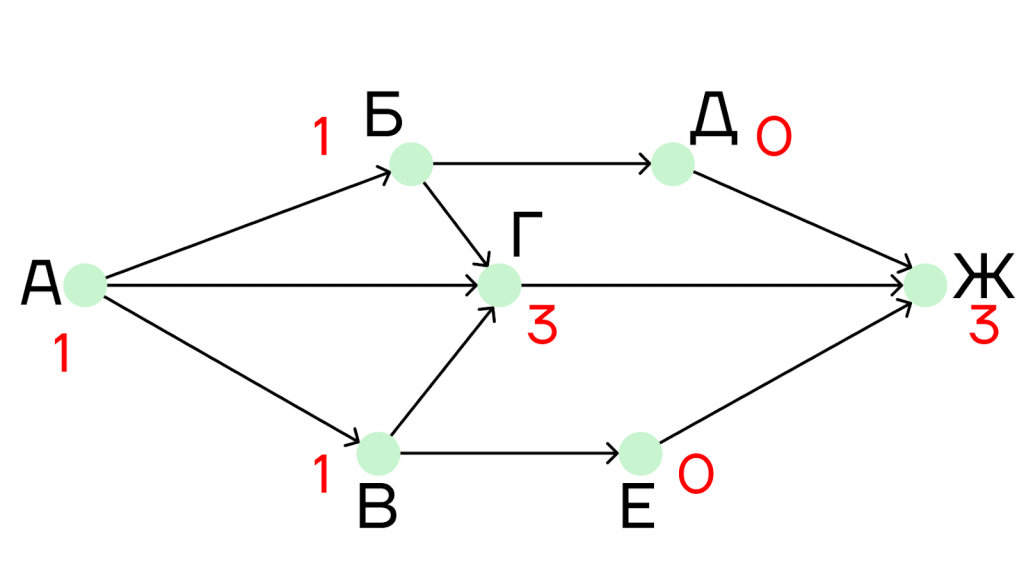
Ответ: 3 

Теперь рассмотрим похожую задачу с немного измененным условием. 

Пример 2. 

Решим задание, аналогичное №9 из ОГЭ.

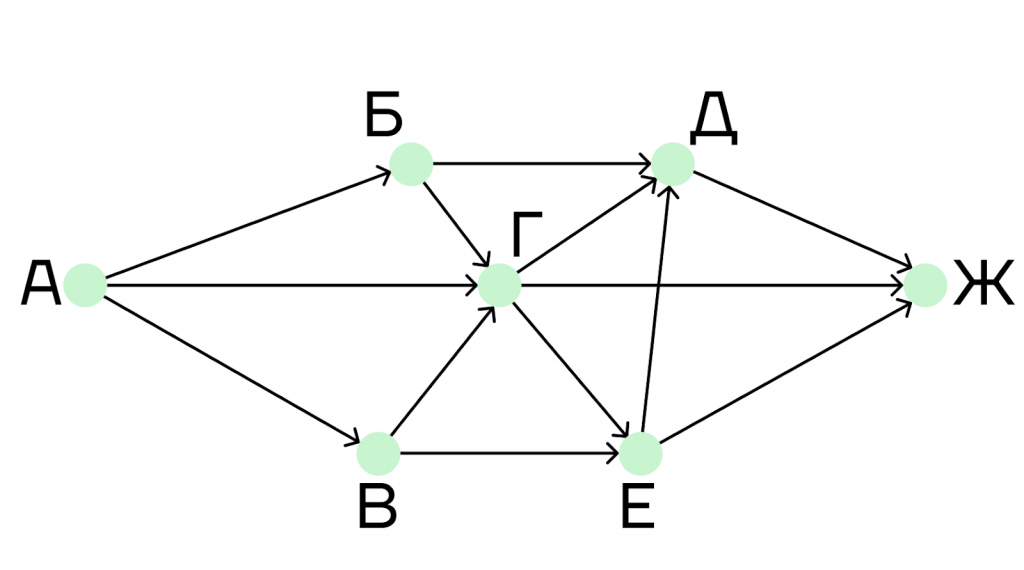
На рисунке дана схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует дорог из города А в город Ж, не проходящих через город Е?

Решение. 

В данном примере дорога из города А в город Ж будет непроходящей траекторией, так как она не должна проходить через город Е.

Эта задача решается так же, как и предыдущая, только здесь мы должны обнулить тот город, через который не должны идти дороги.

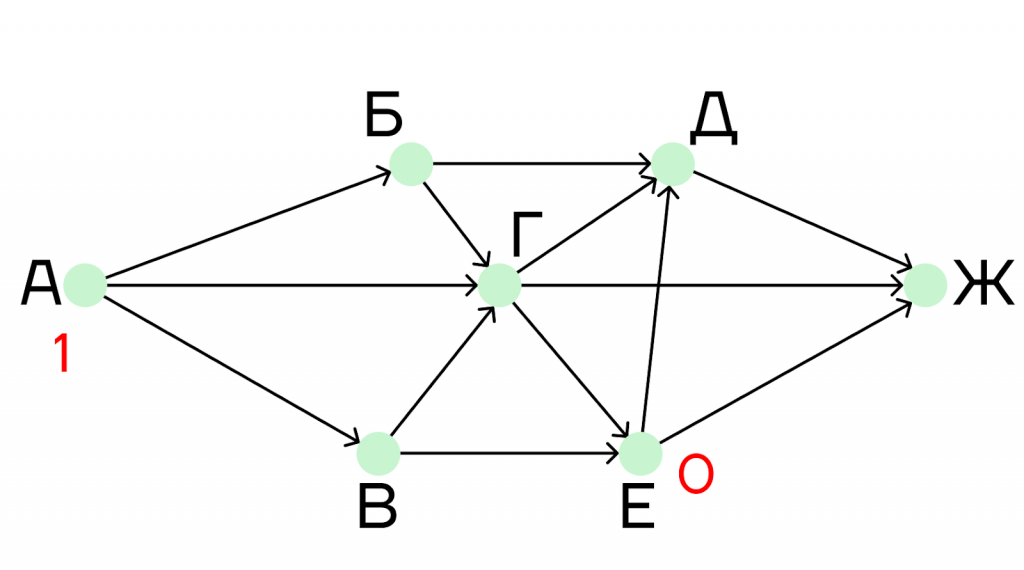
Шаг 1. В первую очередь приписываем единицу к городу А и обнуляем город Е, так как по условию задачи в этот город заходить нельзя.

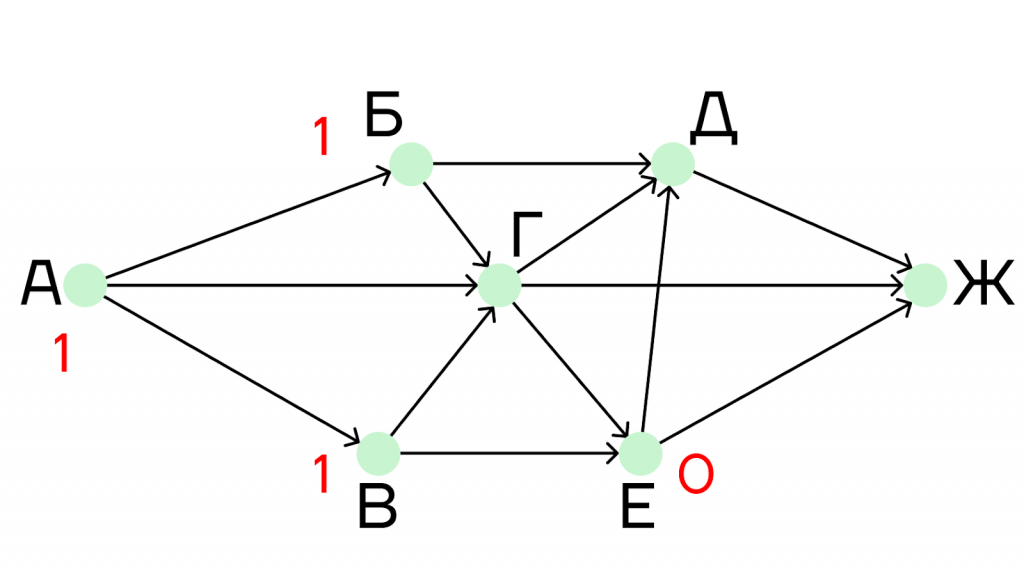
Шаг 2. Рассмотрим город В и город Б. К ним из города А проложено только по одной дороге, поэтому под этими пунктами напишем по единице.

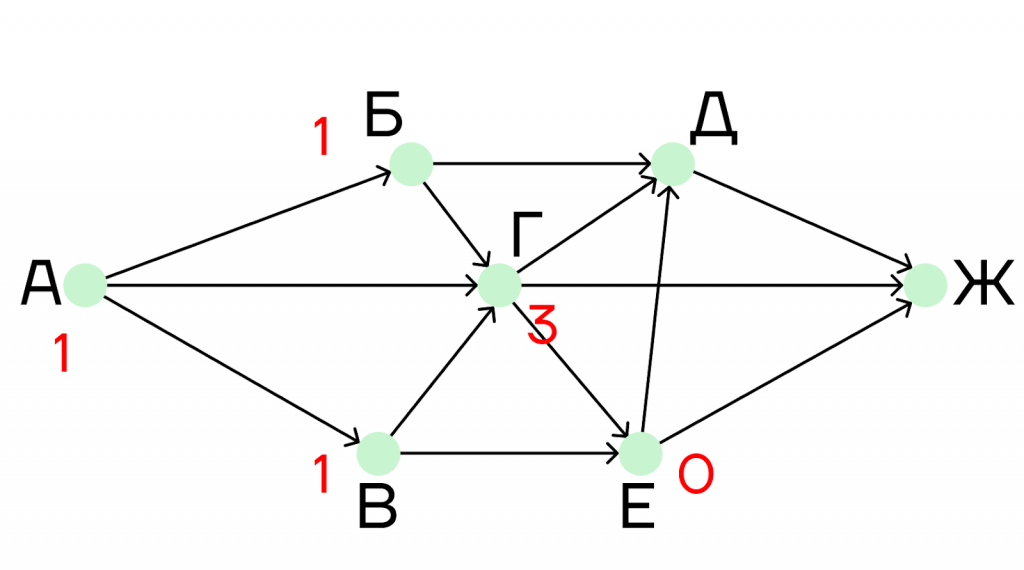
Шаг 3. Теперь рассмотрим город Г. В него ведет три дороги, поэтому под пунктом Г напишем сумму этих трех пунктов:

1 + 1 + 1 = 3

Шаг 4. Следующим будет пункт Д. В него ведет три дороги: из города Б, города Г и города Е. Под пунктом Д напишем сумму:

1 + 3 + 0 = 4

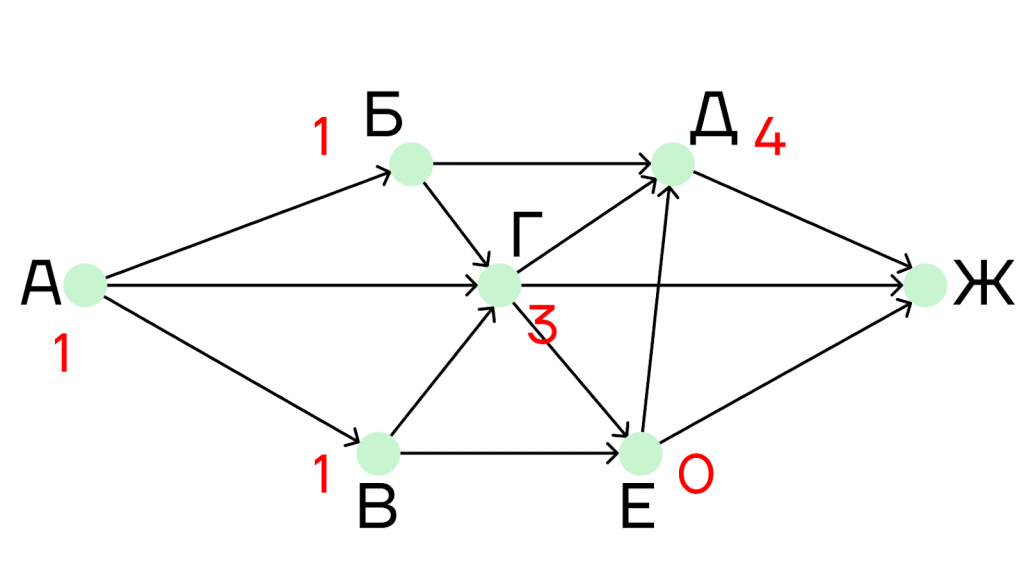
Шаг 5. Последним рассмотрим пункт Ж. В него идут дороги из городов Д, Г, Е. Под пунктом Ж напишем сумму:

4 + 3 + 0 = 7

Получается, что из пункта А в пункт Ж ведет 7 дорог, не проходящих через пункт Е.

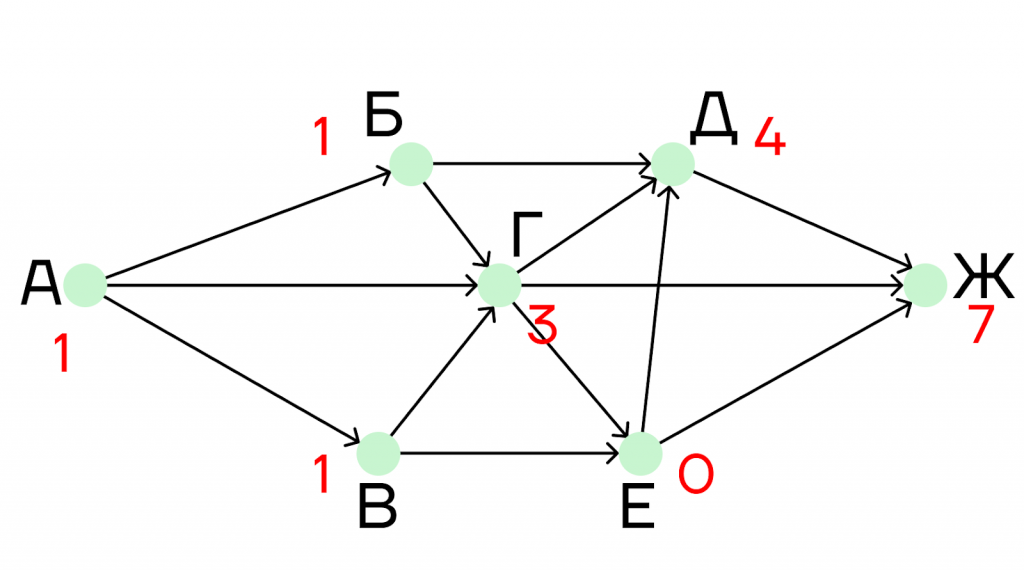
Ответ: 7

Бывает еще один тип такого задания: графы, которые делятся на две части.

Пример 3.
Рассмотрим аналог задания 13 из ЕГЭ.
На рисунке дана схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Необходимо найти количество дорог, ведущих из города А в город Ж.

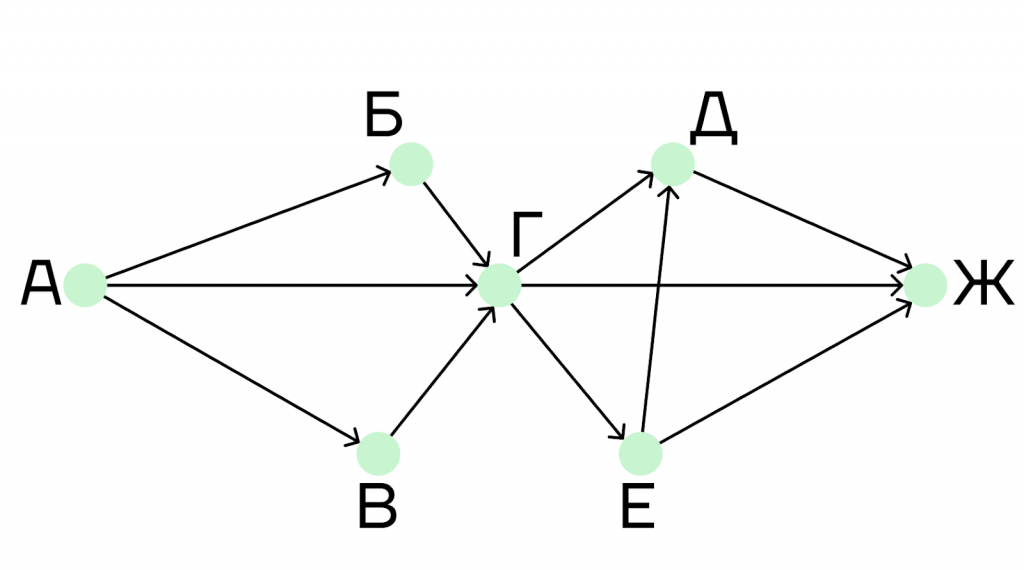
Решение. 

Такие задания проще всего решать разбиением графа на части. Мы будем рассматривать каждую часть графа отдельно, а затем найдем окончательное общее решение. 

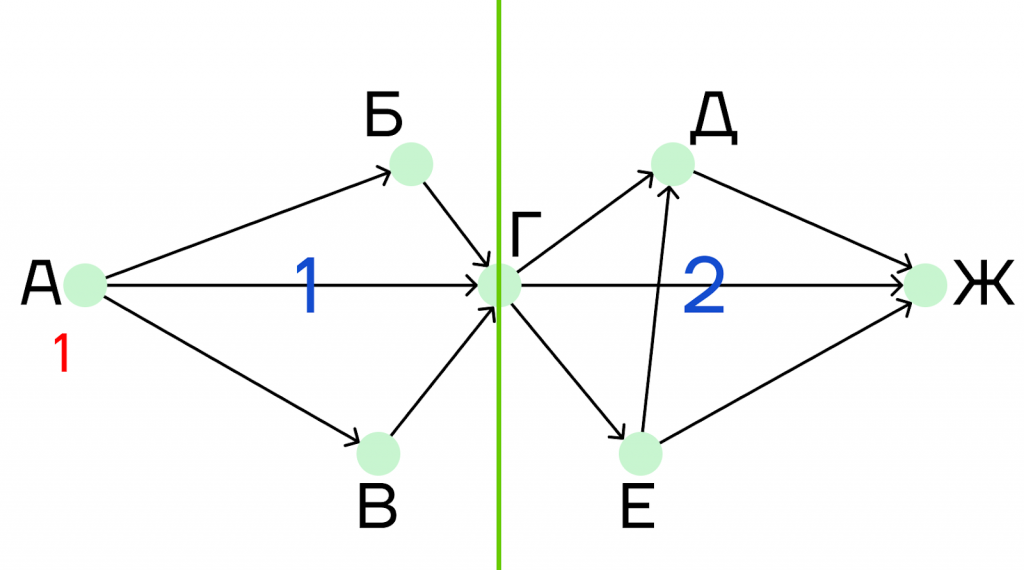
Шаг 1. Рассмотрим первую часть. Будем следовать той же логике, как и в предыдущих задачах:

• Городу А присваиваем значение 1.
• Под пунктами Б и В пишем единицы.

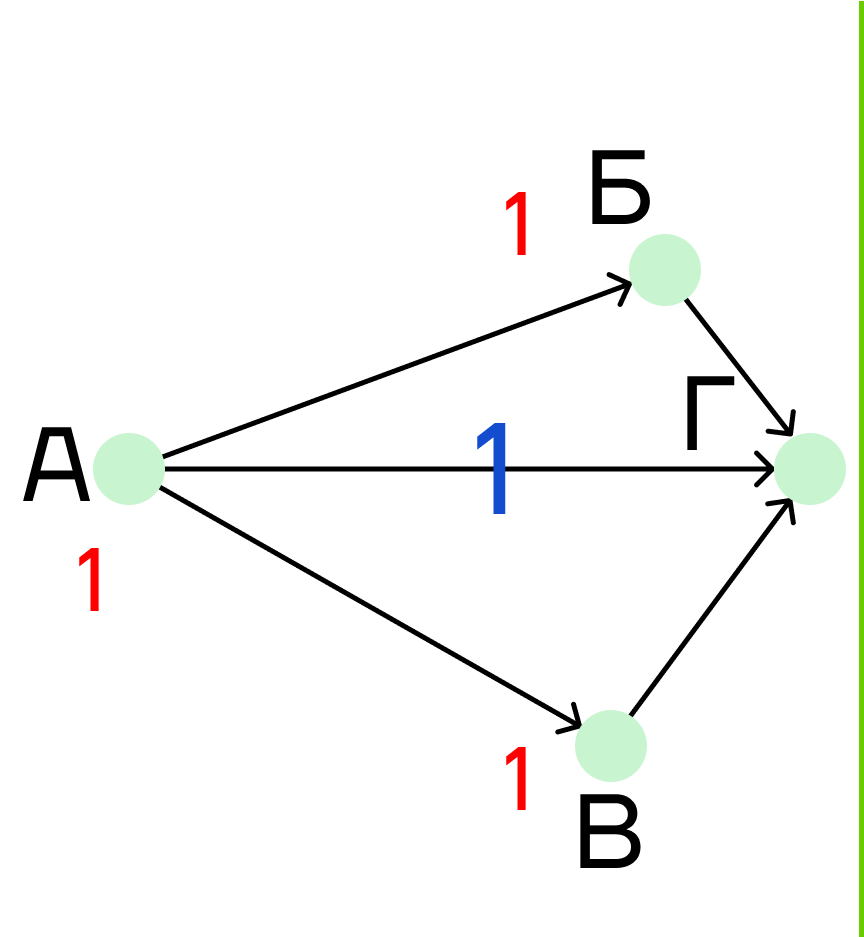
Шаг 2. Решаем первый граф до конца. Для этого находим сумму для пункта Г, в который ведут три дороги:

1 + 1 + 1 = 3

Под пунктом Г пишем 3.

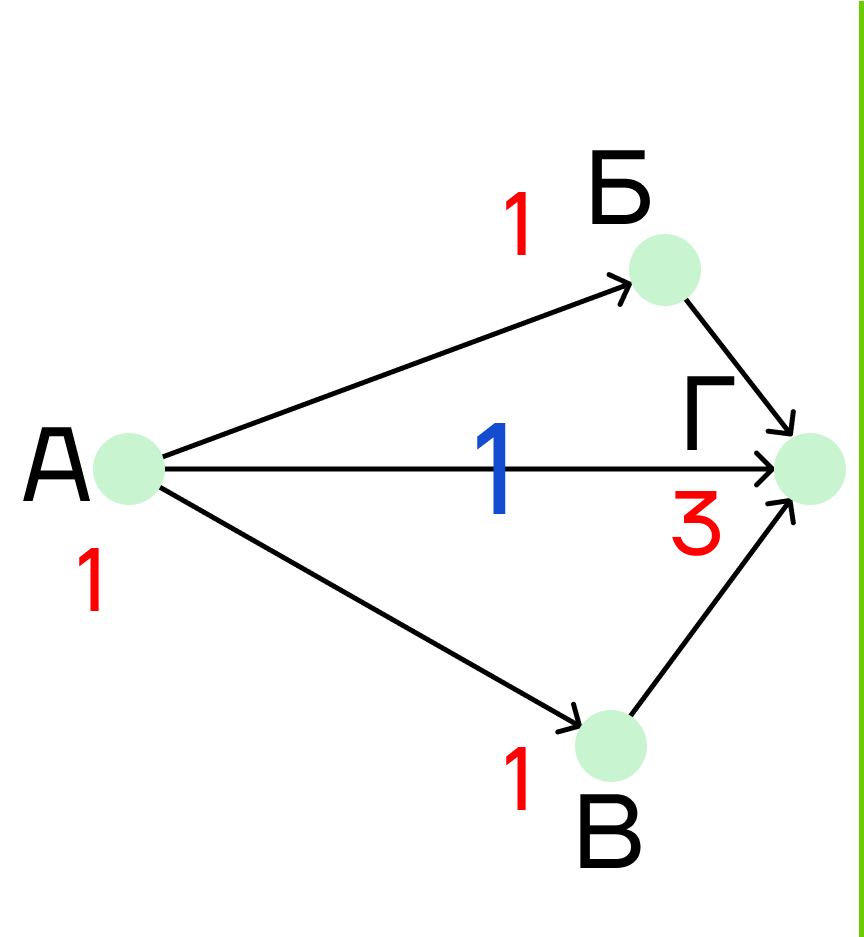
Шаг 3. Теперь рассмотрим вторую часть графа. Здесь нам нужно отбросить решение первой части, поэтому под пунктом Г мы пишем единицу.

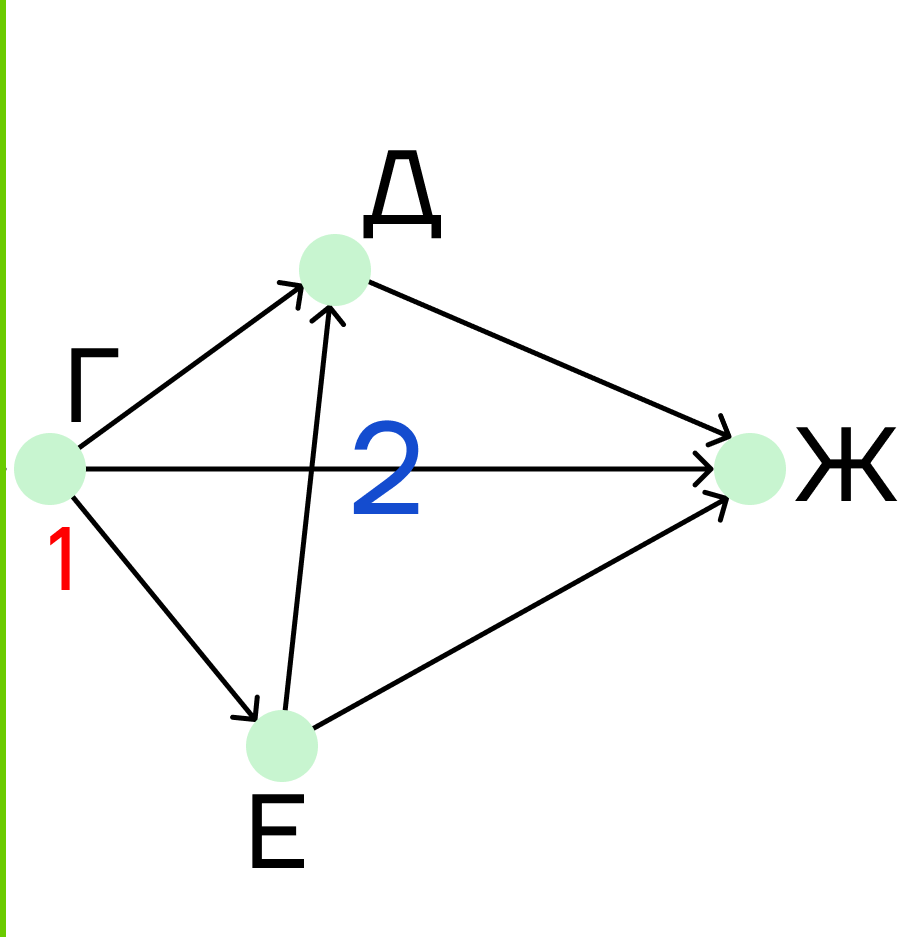
Шаг 4. На очереди город Е. В него ведет одна дорога, поэтому подпишем под пунктом Е единицу.

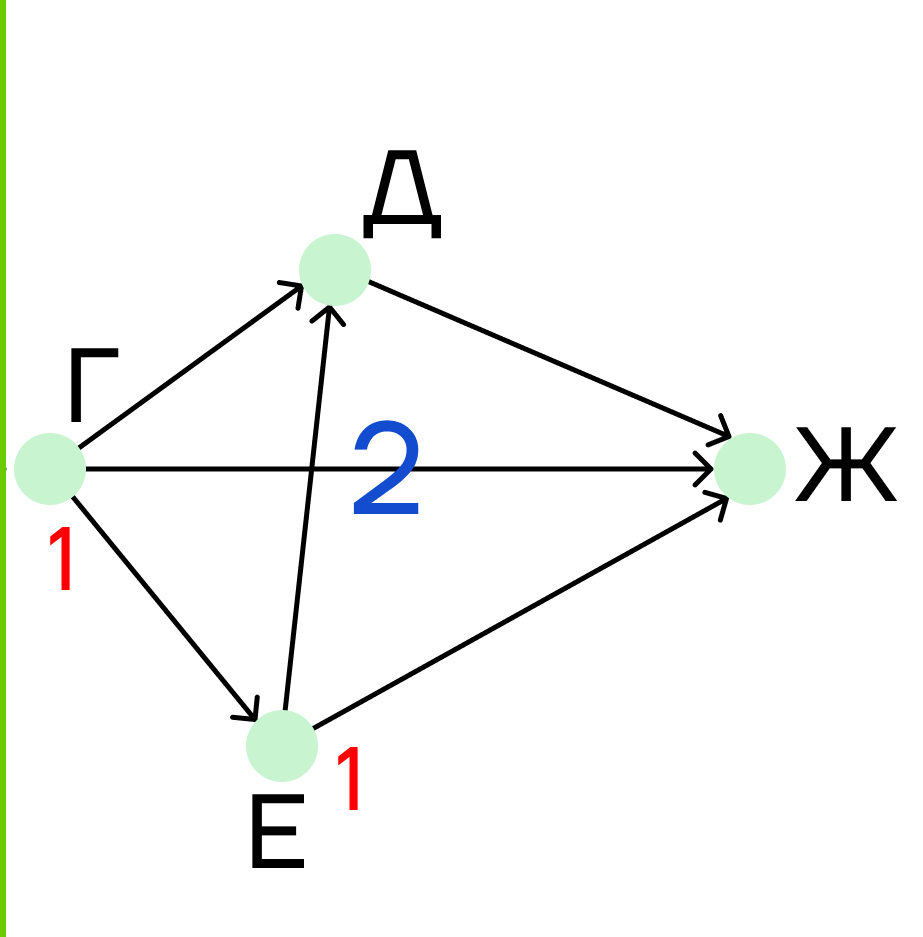
Шаг 5. В пункт Д ведут две дороги, поэтому под ним напишем сумму:

1 + 1 = 2

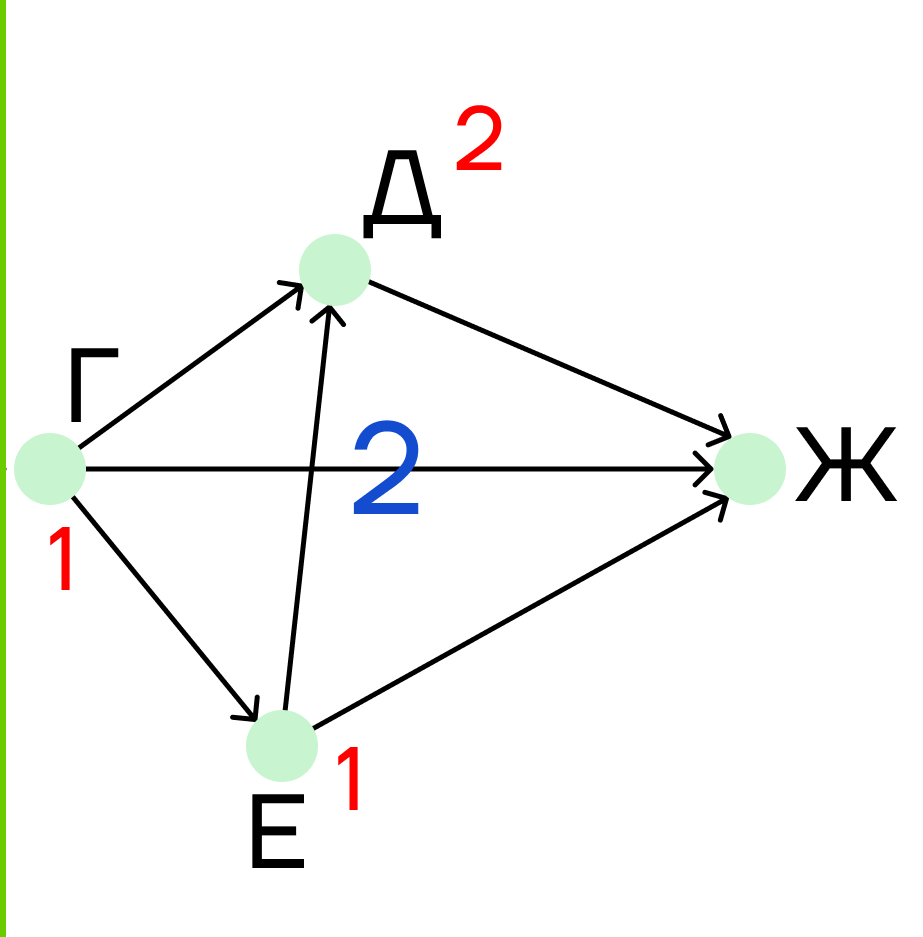
Шаг 6.  В пункт Ж идут дороги из городов Г, Д и Е. Под городом Ж пишем сумму:

1 + 1 + 2 = 4

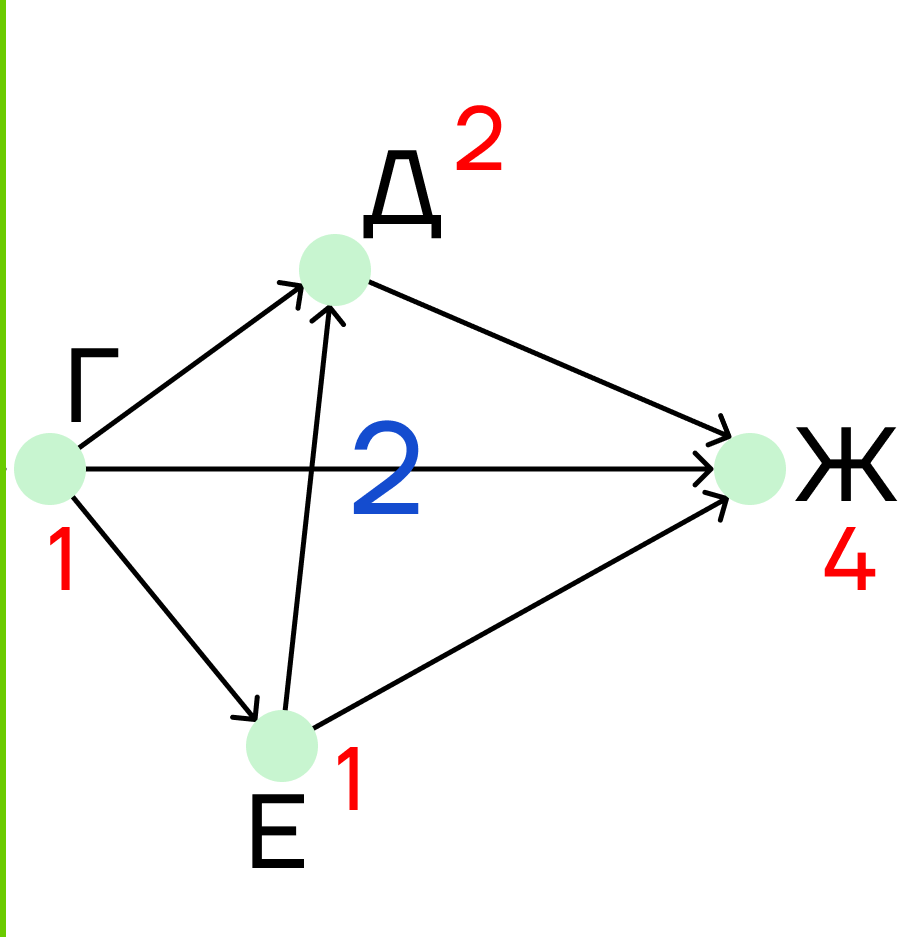
Но это не конец!

Шаг 7. Теперь мы должны найти окончательное решение. Это можно сделать с помощью формулы:

Г(1)* Г(2) = Гобщ, где Г(1) и Г(2) — решения для первого и второго графа.

В нашем случае решением будет произведение:

3 * 4 = 12

Ответ: 12

В этой статье мы разобрались с графами: поняли, какие они бывают, как их можно задать и как решаются задачи с применением графов. Но в нашем учебнике еще много интересного материала, который мы советуем вам прочитать. Например,  статья про теорию игр.

Фактчек

• Граф — это совокупность вершин, часть из которых соединена ребрами. По графу можно двигаться от вершины к вершине по ребрам.
• Если в графе начальной и конечной точкой будет одна вершина, то такой граф будет циклическим.
• Графы называются проходящими, когда при прохождении всей траектории мы проходим все вершины.
• В ориентированном графе каждое ребро имеет свое направление, движение по таким ребрам происходит только по направлению. В неориентированном (двунаправленном) графе по каждому ребру можно двигаться в обе стороны.
• Существуют графы без циклов, они называются деревьями из-за внешнего сходства. Самые верхние точки дерева называются истоками. Стоки — такие вершины дерева, в которые входят ребра, но ни одно ребро не выходит.
• Весовая матрица — способ задания графа с помощью таблицы, на полях которой по высоте и ширине указаны вершины графа, а в их пересечении — значение веса ребра между этими пунктами.
• Для поиска наименьшего пути между вершинами графа можно использовать алгоритм Дейкстры.
• Если в задаче просят найти дороги, не проходящие через какую-то вершину, то мы имеем дело с непроходящей траекторией.
  Если же нам нужно найти количество дорог, проходящих через определенный пункт, то это проходящая траектория.
• Если нам нужно найти решение для большой задачи, то мы можем разделить граф на несколько частей и решить их по отдельности, а потом узнать общее решение с помощью формулы: Г₍₁₎* Г₍₂₎ = Г_общ.

Проверь себя

Задание 1.
Что такое ребро графа?

1. Длина пути между двумя вершинами графа.
2. Путь между двумя вершинами графа.
3. Количество путей, связанных с данной вершиной.
4. Нижняя точка графа

Задание 2.
По данной весовой матрице выберите верные утверждения:

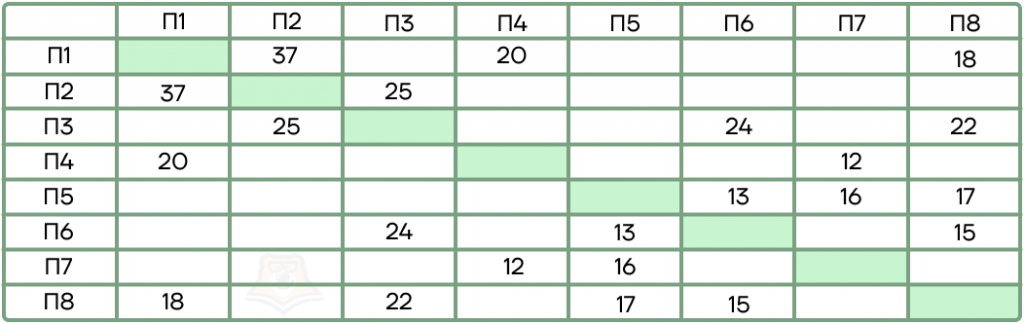
1. Ребра между вершинами П2 в П4 не существует.
2. Вес ребра между П5 и П7 равен 17.
3. Существует ребро между П3 и П7.
4. Эта весовая матрица составлена для ориентированного графа.
5. Эта весовая матрица составлена для неориентированного графа.
6. Длина дороги П1-П8-П5 равна 35.

Задание 3.
Какие утверждения верны для ориентированного графа?

1. Каждое ребро графа имеет свой вес.
2. Каждое ребро графа имеет свое направление.
3. В таком графе нужно пройти через каждую вершину.
4. Движение против направления ребра возможно.

Задание 4.
По весовой матрице определите длину кратчайшего пути из вершины А в вершину Е.

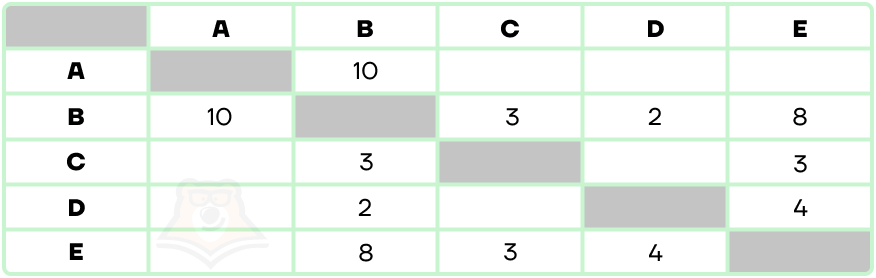
1. 10
2. 13
3. 16
4. 18

Ответы: 1. — 2; 2. — 1, 5, 6; 3. — 2; 4. — 3.