Динамический подход к решению задач
На этой странице вы узнаете
- В каких случаях удобно использовать динамическое решение?
- Как Python может облегчить нашу жизнь?
- Чему нужно поучиться у Финеса и Ферба?

Подозвал старец своих сыновей, дал им веник и сказал сломать его.
— Мы не можем, отец, — ответили они ему.
Тогда старец развязал веник и сказал им ломать прутья по отдельности.
— Это очень просто, отец, — сказали они ему.
— В этом и заключается идея динамического подхода к решению задач, — ответил он им.
А теперь давайте разбираться, как динамический подход облегчает жизнь и чем он нам может быть полезен.
Принцип динамического подхода
Раньше для сложных операций приходилось часами проводить длинные математические вычисления, но сейчас такие задачи можно решить буквально за пару минут с помощью динамического подхода. В этой статье мы разберемся с тем, в чем заключается этот подход, когда его использовать и как реализовать его с помощью кода на Python.
Идея динамического решения заключается в том, чтобы разбивать сложную задачу на несколько более простых и маленьких заданий. Используя решения мелких задач, мы приходим к общему решению.
Таким образом, план динамического решения состоит в следующем:
- Разбиение задачи на небольшие части.
- Поиск решения подзадач.
- Использование решений мелких частей для нахождения общего решения.

Подзадачи также решаются делением их на еще более простые части до того момента, пока не найдется такая подзадача, которая решается моментально.
Можно сказать, что при подготовке к экзаменам вы тоже пользуетесь динамическим подходом:
- Чтобы хорошо сдать экзамен, нужно научиться решать каждое задание.
- Чтобы решить задание, нужно изучить все подтипы одной задачи.
- Чтобы изучить все подтипы, нужно прочитать теорию для этого задания.
Так, глобальная задача «Сдать экзамен на “отлично”» превратилась в список необходимых действий. Теперь мы будем действовать так: выполняем самую маленькую задачу, потом еще одну и еще, они приведут нас к тому, что вскоре мы сможем решить задачу побольше. Хорошо поработав и решив все мелкие задачи, мы сможем добраться и до глобальной.
Динамическое решение задач на графы
| В каких случаях удобно использовать динамическое решение? Поиск оптимального маршрута в задачах на графы — хороший пример задачи, которая легче решается динамически, причем в каком бы то ни было виде. |
Например, нам дана цель максимально быстро пройти через болото из одного его конца в другой. Карта самого этого болота представлена в виде таблицы, каждый сектор которой имеет значения опасности и дискомфорта.
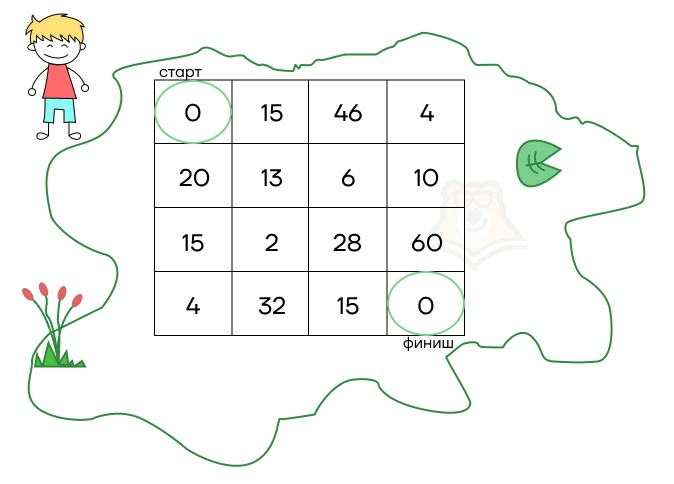
Раз добраться надо максимально быстро, будем двигаться только по направлению к финишу — вниз и вправо. Но также мы хотим набрать как можно меньше очков опасности и дискомфорта. Мы не любим опасность и дискомфорт. Каждый раз, заходя в ячейку, мы «собираем» значение из нее, накапливая очки.
Наша глобальная задача: узнать, какое наименьшее возможное количество очков дискомфорта мы можем собрать, пройдя по всему болоту.
Разбивая эту задачу на подзадачи, будем постепенно узнавать наименьшие значения собранных очков там, куда мы можем пройти:
- Можем узнать, сколько мы получим очков в ячейках, соседних с начальной.
- Зная новые значения, узнаем соседние уже с ними. Выберем наименьшее значение там, где это возможно.
- Продолжим заполнять соседние ячейки, пока не дойдем до самого конца.
Для удобства и большего взаимопонимания можем пронумеровать все ячейки и сразу сделать первые возможные шаги из начальной позиции вправо и вниз.
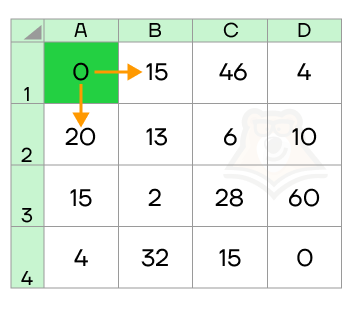
Так как в ячейке А1 нет никакого начального значения очков, в ячейках В1 и А2 останутся соответствующие им значения.
Следующие шаги мы уже делаем из этих позиций. Мы можем пройти вправо или вниз. К ячейкам, в которые мы заходим, будем прибавлять значение предыдущих пунктов. Пройдя через них, мы соберем их значения.
В С1 и А3 можно прийти только с одной стороны: слева и сверху соответственно. Для В2 есть выбор — пройти сверху или слева?
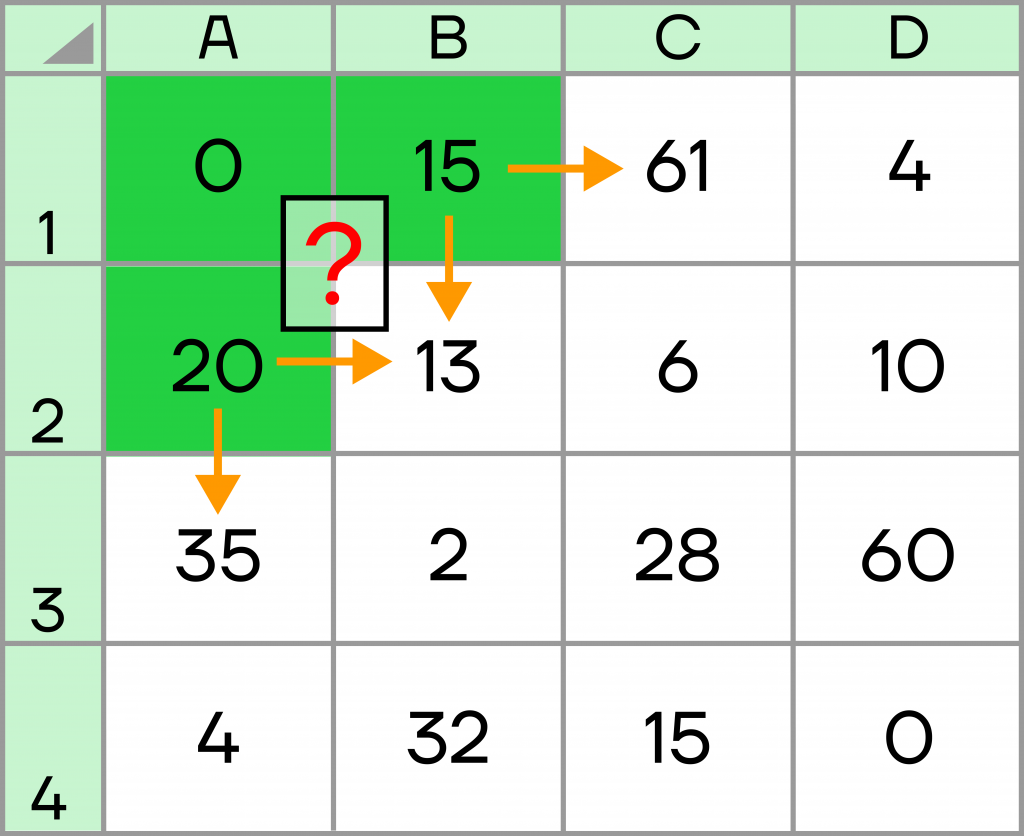
Так как мы хотим собрать наименьшее возможное количество очков, будем идти в В2 из наименьшего варианта.
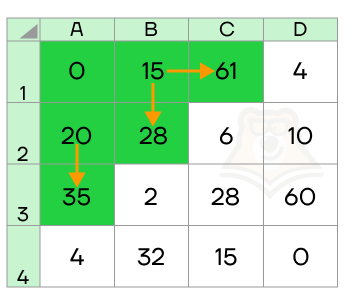
Эта логика продолжается — с помощью ячеек, в которых мы нашли кратчайшие пути, ищем оптимальные пути в следующие — А4, В3, С2 и D1.
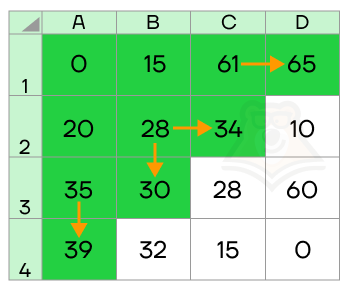
И так до самого конца, пока не найдем значение в интересующей нас ячейке D4:
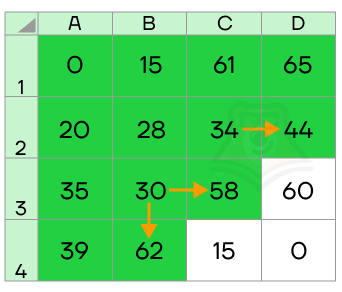
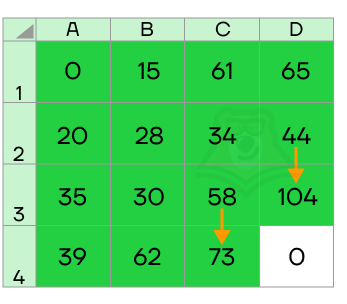
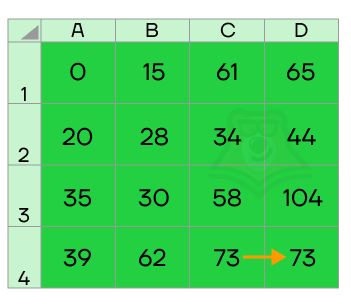
Применяя метод динамического решения, мы находили наименьшие возможные собранные значения очков в каждой ячейке, до которой смогли добраться. Используя эти значения, мы определяли, какие значения будут собраны дальше, и повторяли до тех пор, пока не нашли значение в самой последней ячейке.
Динамическое программирование
Вспомним принцип работы рекурсивной функции из статьи «Функция и рекурсия». Она при необходимости может вызвать саму же себя с другими входными значениями. Здесь можно провести аналогию с методом динамического решения. И там, и там для подсчета итогового результата будут высчитываться промежуточные значения.
| Как Python может облегчить нашу жизнь? Для решения динамических задач программированием можно использовать рекурсивную функцию. Так мы «скинем» всю работу по решению на программу, а сами потратим время на что-нибудь приятное. |
Рассмотрим это на примере поиска чисел Фибоначчи.

Для начала вспомним, что такое числа Фибоначчи.
Числа Фибоначчи — это математическая последовательность, в которой каждое число является суммой двух предыдущих.
Первое и второе числа Фибоначчи — единицы. Каждое последующее число будет суммой двух предыдущих.
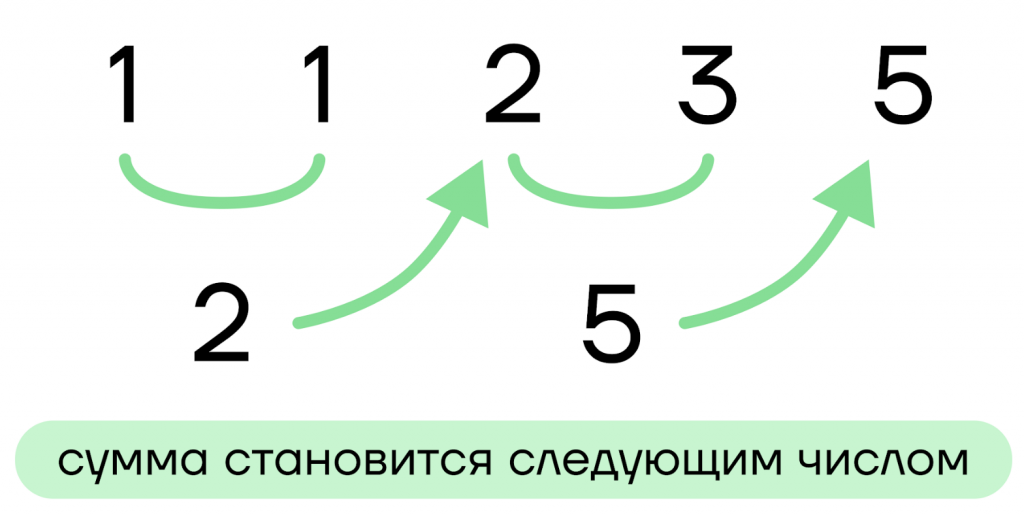
Например, мы хотим найти пятое число Фибоначчи, обозначим его как Fib(5).
При ручном решении мы бы искали его как сумму двух предыдущих чисел Фибоначчи, а предыдущие числа — как сумму предыдущих для них:
- Fib(5) = Fib(4) + Fib(3)
- Fib(4) = Fib(3) + Fib(2)
- Fib(3) = Fib(2) + Fib(1)
- Fib(2) = 1
- Fib(1) = 1
Найдя исходные значения, которые мы знаем, мы двигались бы в обратную сторону, высчитывая каждое следующее число Фибоначчи, пока не нашли бы значение нужного:
- Fib(3) = Fib(2) + Fib(1) = 1 + 1 = 2
- Fib(4) = Fib(3) + Fib(2) = 2 + 1 = 3
- Fib(5) = Fib(4) + Fib(3) = 3 + 2 = 5
Похожим принципом будет работать и рекурсивная функция — только с нашими минимальными усилиями:
- Объявим ее командой def и передадим ей на вход номер числа Фибоначчи, которое мы хотим найти.
- Запишем условие выхода — первое и второе число Фибоначчи равны единице.
- Если число не первое и не второе, оно равно сумме двух предыдущих.
Код программы:
def Fib(n):
if n == 1 or n == 2:
return 1
else:
return Fib(n — 1) + Fib(n — 2)
print(Fib(5))
Вывод программы: 5
Динамический подход к решению задач используется в основном в заданиях 16 и 23 ЕГЭ. Рекурсия помогает сделать решение этих задач более быстрым и эффективным.
Для примера рассмотрим задание №16 ЕГЭ:
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
— F(1) = 2;
— F(n) = 6 * n + F(n — 2), если n нечетно и n > 1;
— F(n) = n * F(n — 3), если n четно и n > 1.
Чему равно значение функции F(12)? В ответе запишите только целое число.
Решение.
1. Сначала создадим функцию F(n) с помощью def F(n).
2. Опишем условия с помощью условного оператора if. Получим:
— Для F(1) = 2:
if n == 1:
return 2
— Для F(n) = 6 * n + F(n — 2) создадим условие, которое будет срабатывать лишь в случае, если n нечетно и n > 1. Получится так:
if n % 2 != 0 and n > 1:
return 6 * n + F(n — 2)
— Для F(n) = n * F(n — 3), если n четно и n > 1, построим аналогичный код:
if n % 2 == 0 and n > 1:
return n * F(n — 3)
3. Выводим через print значение функции F(12), и наша программа готова.
Полный код программы:
def F(n):
if n == 1:
return 2
if n % 2 != 0 and n > 1:
return 6 * n + F(n — 2)
if n % 2 == 0 and n > 1:
return n * F(n — 3)
print(F(12))
Запустим получившуюся программу и получим ответ — 1752.
Ответ: 1752
Нестандартные задачи на динамический подход
Задачи на динамический подход отличаются от большинства заданий ЕГЭ и ОГЭ тем, что часто в их решении нужно не просто использовать один и тот же алгоритм, но и применять нестандартные методы решения.
Многие пугаются, увидев новый тип задания, но для того, чтобы решить нестандартную задачу, нужно всего лишь вспомнить Финеса и Ферба.
| Чему нужно поучиться у Финеса и Ферба? Эти ребята точно знают толк в творческом решении задач! Их главным секретом было то, что на любую сложность они смотрели с интересом и пытались нестандартно справиться с ней. Так будем делать и мы. |

Рассмотрим задачу: Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
- Отнять 1.
- Разделить на 2.
Вторая команда осуществляется только для четных чисел.
Вопрос: Сколько существует программ, для которых при исходном числе 15 результатом является число 1 и при этом траектория вычислений не содержит число 10?
Перед тем, как решать данную задачу, нужно вспомнить одно важное понятие.
Траектория вычислений — это «путь» от первого до последнего числа, который проходит программа. То есть некоторая цепочка результатов вычислений программы, которая получается при исполнении команд.
Рассмотрим траекторию вычислений на примере. Допустим, у нас есть программа, которая начинается в числе 2 и заканчивается в числе 8. При этом она использует для изменения чисел только одну команду: «прибавить 2». В таком случае:
2 + 2 = 4
4 + 2 = 6
6 + 2 = 8
В этом примере траектория вычислений будет такой: 2, 4, 6, 8.
А теперь перейдем к нашей задаче.
Решение.
Эта задача может поставить в тупик, если вы никогда не решали подобные. Но если присмотреться, то это обычное задание №23 ЕГЭ, просто с измененными действиями. Поэтому, заручившись поддержкой Финеса и Ферба, придумываем нестандартное решение.
Шаг 1. Пользуемся правилом деления проблем на «проблемки», разделим задачу на много маленьких подзадач.
Итак, нам нужно рассмотреть все числа и подсчитать, сколько существует программ, которые приведут нас к каждому числу. Первым делом найдем количество команд, ведущих двойку к единице:
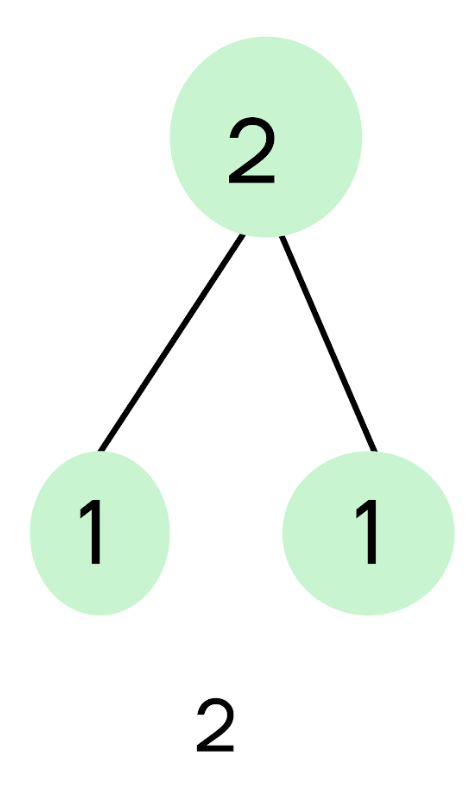
Поскольку два — это четное число, мы можем его разделить на 2. При этом мы можем и отнять 1 и получить 1.
Таким образом, у нас получается два варианта: 2 – 1 = 1 и 2 / 2 = 1. Важно помнить, что это две разные программы, хоть они и ведут к одному результату. То есть у нас есть две команды, ведущие нас к единице.
Для нашего удобства будем отмечать количество программ, ведущих данное число к единице, под всеми числами.
Из двойки в единицу идет две программы, поэтому под ней мы напишем число 2.
Шаг 2. Следующим числом будет 3:
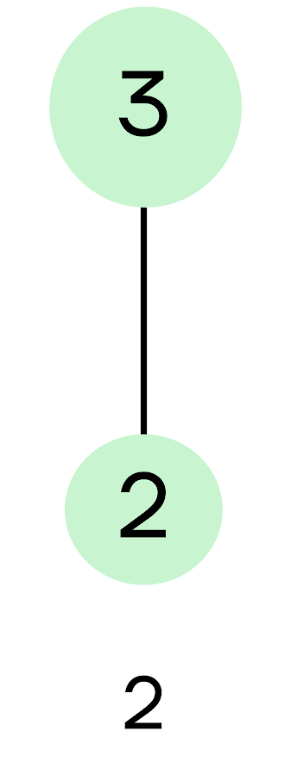
Поскольку три — это нечетное число, мы можем лишь отнять единицу, разделить на 2 у нас не получится. Тогда наш единственный вариант:
3 – 1 = 2
Чтобы узнать, сколько существует программ, превращающих тройку в единицу, нужно посмотреть на количество программ у числа, в которое превращается 3. В нашем случае это число 2, которое, в свою очередь, имеет две программы превращения в единицу.
Приходим к выводу, что в тройку ведет две команды, поэтому пишем под схемой 2.
Шаг 3. Переходим к следующему числу – четверке. С ним мы будем работать так же, как делали это в шаге 1 с двойкой:
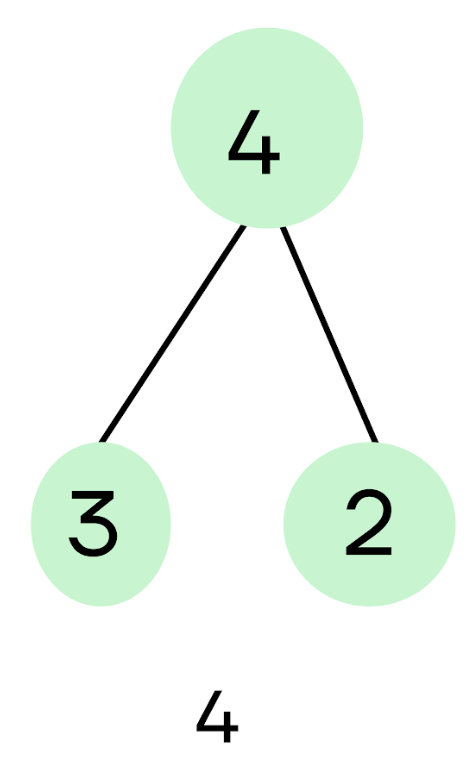
При исполнении первой команды «отнять 1» мы получим 4 – 1 = 3. Мы уже считали количество программ у тройки: их было две.
Теперь рассмотрим вторую команду «разделить на 2». Так как четверка – четное число, мы можем применить и эту команду: 4 : 2 = 2. Для двойки также известно число команд – их две.
Так как из четверки можно попасть в два пункта, количество программ, ведущих из четверки в единицу, вычисляется как сумма программ тех чисел, в которые превращается четверка.
Из тройки идет 2 команды, из двойки также идет 2 команды, следовательно, из четверки ведет 2 + 2 = 4 команды. Это число и пишем под схемой.
Шаг 4. Рассмотрим пятерку. Сразу заметим, что число нечетное, поэтому к нему можно применить только первую команду «отнять 1»:
5 – 1 = 4
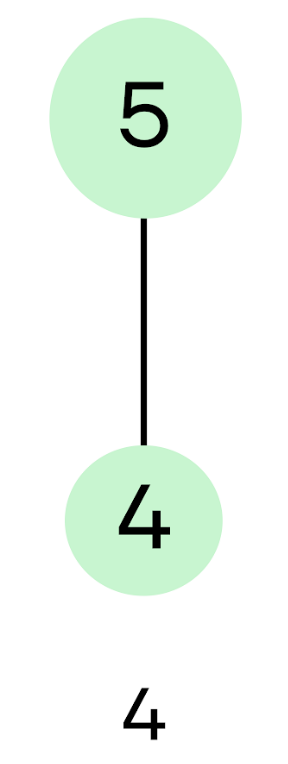
Это значит, что из пятерки можно прийти только в четверку, и количество команд, ведущих пятерку в единицу, будет таким же, как и у четверки – 4. Пишем 4 под схемой.
Шаг 5. Мы продолжаем разбирать все числа, останавливаясь лишь на числе 10, потому что в условии сказано, что 10 не входит в траекторию вычислений. В таком случае мы просто обнуляем данное число:
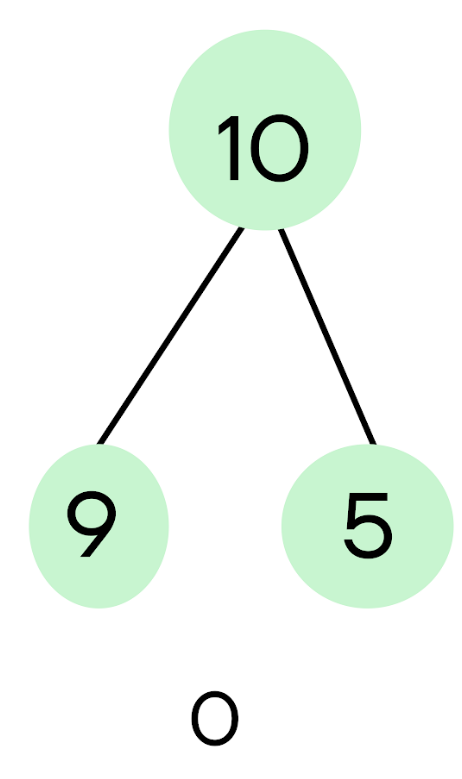
Шаг 6. Рассмотрев все числа, получаем:
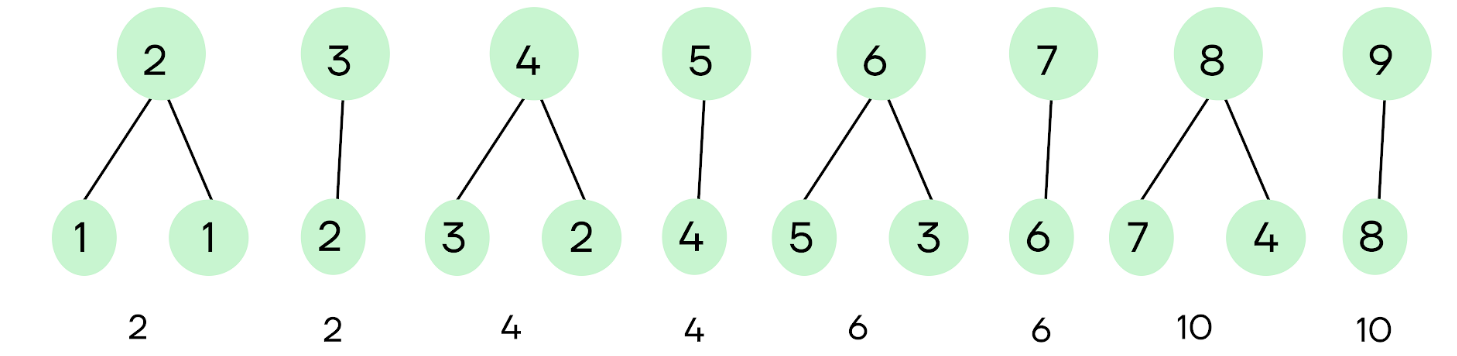
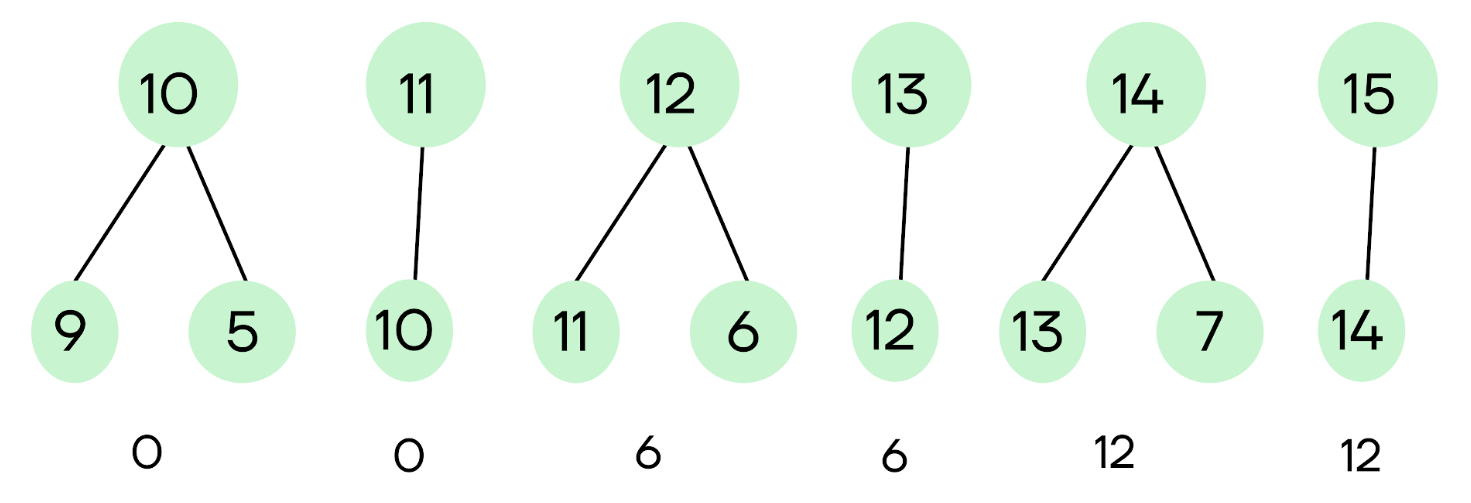
В данной задаче получился ответ 12.

Динамическое решение задач – очень классный навык, который поможет решить многие задания на экзамене. Принцип разбиения задач на маленькие кусочки используется не только в информатике, но и в жизни, так что, научившись использовать данный метод при решении заданий, вы также сможете привнести данный принцип в повседневную жизнь.
При динамическом подходе в решении задач мы часто должны использовать программирование. В нашем учебнике есть очень полезная статья «Ошибки Python». Она рассказывает про частые ошибки при написании программ, поэтому мы крайне советуем ее прочитать и никогда не совершать этих ошибок.
Термины
Натуральные числа — это числа, возникающие естественным образом при счете: 1, 2, 3, 4, 5, 6, 7 и так далее.
Фактчек
- Принцип динамического подхода заключается в разбиении целостной задачи на маленькие подзадачи и поиске итогового ответа на основе решения этих подзадач.
- Каждая подзадача решается разбиением ее на еще более мелкие подзадачи до тех пор, пока мы не получим самую простую подзадачу, ответ на которую известен заранее или может быть рассчитан простым действием.
- Для реализации динамического решения программой из-за схожести принципа работы используется рекурсивная функция.
Проверь себя
Задание 1.
Что подразумевает метод динамического решения задачи?
- Быстрое, веселое и энергичное решение задачи под музыку.
- Решение задачи строго по описанному в условии алгоритму.
- Разбиение задачи на более мелкие подзадачи.
Задание 2.
Реализация динамического решения задачи программированием…
- … невозможна.
- … осуществляется с помощью вложенных циклов.
- … осуществляется с помощью рекурсии.
Задание 3.
Вернитесь чуть выше, к задаче про болото. Какой был бы ответ на эту задачу с той же таблицей, если бы надо было собрать не наименьшее, а наибольшее количество очков?
- 155
- 71
- 73
- 110
Задание 4.
Найдите восьмое число Фибоначчи, если первые два числа – единицы:
- 21
- 19
- 26
- 13
Ответы: 1. — 3; 2. — 3; 3. — 1; 4. — 1.


 к списку статей
к списку статей





