Системы счисления
На этой странице вы узнаете
- В каких случаях 10 не равно 10?
- Как купить шоколадку у инопланетянина?
- А если межгалактическая торговля нам все-таки доступна?
Привычная нам система счисления называется десятичной, потому что нам с детства удобно считать 10 пальцев на руках. Но так было не всегда: раньше людям было удобнее считать до 12, по количеству фаланг на пальцах одной руки. Для них и для нас число 10 имеет совершенно разное значение. А вот к чему это в итоге привело, мы узнаем в этой статье.
Виды систем счисления
Система счисления — это модель, которая позволяет записывать числа по определенным правилам.
Если упростить это определение, то можно сказать, что это набор правил, по которым мы считаем.
Основных типов систем счисления 2:
- позиционные,
- непозиционные.
Непозиционные системы счисления основываются на том, что значение цифр никак не зависит от того, на какой позиции в числе они находятся.
Возьмем фермера и его овец. Какой способ записать количество овец самый удобный?
Самый простой пример — подсчет с помощью одной насечки. Тогда фермер подсчитывает овец в своем стаде поштучно, обозначая при записи каждую отдельной засечкой.

Очевидно, что это неудобно. В интересах фермера размножать овец. Но чем их больше, тем менее читаема такая запись. Когда он добьется невиданных высот в скотоводстве и у него станет 2796 овец, их подсчет с помощью одной засечки будет неудобен, ведь их слишком много.
Римская система счисления — еще один известный пример непозиционной системы счисления (хотя и есть исключения, например, в виде цифр 4 (IV) или 6 (VI), но все-таки эту систему относят к непозиционной). В ней уже появляются символы для обозначения отдельных чисел. Но, в какой бы позиции символ ни стоял, он все еще значит только самого себя:
- I — 1;
- V — 5;
- X — 10 и так далее.
Римская система счисления упрощает запись чисел, но не решает проблему неудобства чтения полностью. Например, число 2796 в римской записи будет выглядеть как MMDCCXCVI. Уже неприятно.
В позиционных системах счисления значение цифры зависит от того, на какой позиции она стоит. Эта позиция называется разрядом.
На примере нашей родной десятичной системы счисления мы с вами понимаем, что в числе 1234:
- 1 — количество тысяч, и обозначает не 1, а 1000;
- 2 обозначает количество сотен и понимается как 200;
- 3 отвечает за количество десятков и означает 30;
- 4 стоит на самой последней позиции и означает количество единиц, поэтому в данном случае 4 — это 4.
Это сильно упрощает чтение чисел любого размера, так как меняется сам принцип их чтения:
- В непозиционной системе счисления (на примере римской): СХХIII = 100 + 10 + 10 + 1 + 1 + 1 = 123.
- В позиционной: 123 = 100 + 20 + 3.
Именно позиционную систему счисления выберет грамотный фермер, чтобы подсчитать количество овечек.
Теперь, когда мы разобрались с тем, что представляют собой позиционные и непозиционные системы счисления, нам необходимо определить основные виды позиционных систем счисления, так как именно с ними мы и будем работать дальше.
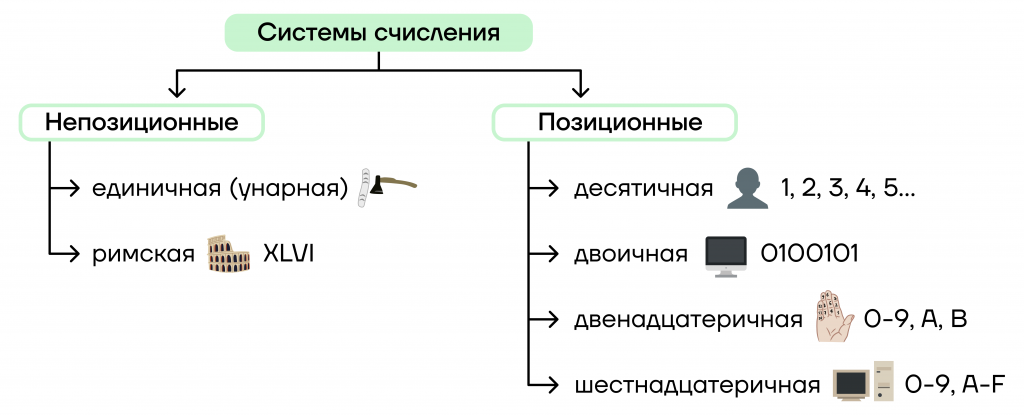
Основание позиционной системы счисления
Позиционная система счисления характеризуется ее основанием — количеством цифр, которые она использует для записи чисел.
- Десятичная система счисления (10сс) использует 10 цифр — от 0 до 9, с ней мы знакомы с детства.
- Компьютеру роднее двоичная система счисления (2сс), которая использует 2 цифры — 1 и 0.
- В двенадцатеричной системе счисления (12сс) помимо цифр 0–9 необходимы еще два символа. Для удобства их заменили буквами: A = 10, B = 11. Так получилось 12 символов от 0 до B.
- Также небезызвестная система счисления — шестнадцатеричная (16сс). Для нее кроме цифр 0–9 нужно еще больше символов, чтобы обозначить все цифры. Происходит это по аналогии — каждая новая буква отвечает за большее значение: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
| В каких случаях 10 не равно 10? Мы используем числа тогда, когда кончаются цифры. Привычная нам система счисления называется десятичной, потому что использует 10 цифр — от 0 до 9. Для записи значений больше 9 мы начинаем строить числа из нескольких цифр. Первое такое число — 10. Если бы мы использовали другое количество цифр, все выглядело бы иначе. При использовании цифр от 0 до 6 нам пришлось бы строить числа уже для записи значений, больших 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления. |

Построение числа в непривычных нам системах счисления происходит точно так же, как и в 10сс:
- Увеличиваем значения единиц, используя доступные цифры.
- Как только цифры закончились, значение единиц обнуляется. Появляется новый разряд десятков, который также увеличивается от 1 до предела системы счисления.
- Когда любой разряд числа принимает значение максимальной цифры — разряд выше увеличивается на 1, а текущий разряд обнуляется.
Например:
- В 10сс число 88 будет увеличиваться так:
88 → 89 → 90 → 91 → 92 → … 99 → 100.
- В 2сс разряды будут появляться быстрее из-за маленького количества цифр:
1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000.
- В 12сс чуть медленнее, так как цифр больше:
8 → 9 → A → B → 10 → 11 → … 18 → 19 → 1A → 1B → 20 → … 99 → 9A → 9B → A0 → A1 → … AA → AB → B0 → B1 → … BA → BB → 100.

Арифметика, как и построение числа, во всех системах счисления одинакова:
- Изменение разрядов происходит с единиц.
- При сложении избыток суммы увеличивает разряд выше (то самое «6 пишем, 1 в уме»).
- В вычитании при необходимости занимаем значение из старшего разряда, уменьшая его на 1.
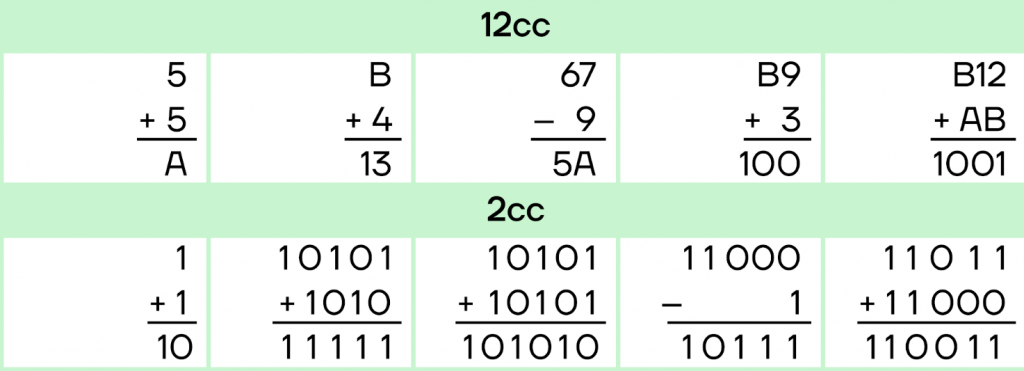
Возникает вопрос: можно ли переводить числа из одной системы счисления в другую? Разумеется, можно. Для этого есть несколько способов, которые лежат в основе всех алгоритмов переводов чисел из одной системы счисления в другую.
Расширенная запись числа и перевод из Nсс в 10сс
| Как купить шоколадку у инопланетянина? Уметь переводить числа из 10сс в другие и обратно важно для того, чтобы торговать с инопланетянами. Однажды мы, вероятно, достучимся до внеземных цивилизаций. Но у них может оказаться не 10 пальцев на руках, а 7, 12 или любое другое количество. Если их представления о математике шли путем, подобному нашему, какую систему счисления придумали они? Когда мы захотим купить инопланетный сникерс за 2256 межгалактических юнитов, вполне может оказаться, что наши представления о числах сильно отличаются. |

Подсчитав количество пальцев на руках продавца шоколадок, мы должны научиться переводить числа из одной системы счисления в другую.
Полная запись числа \(a_1a_2a_3…a_i…a_k\), где ai — цифра числа под номером i, состоящего из k символов и с основанием системы счисления n, будет выглядеть как:
\(a_1a_2a_3…a_i…a_k=a_1*n^{k — 1}+a_2*n^{k — 2}+…+a_i*n^{k — i}+…+a_k*n^0\).
На примерах:
- 123 в 10сс расписывается как: \(1*10^2+2*10^1+3*10^0\);
- 1010 в 2сс: \(1*2^3+0*2^2+1*2^1+0*2^0\);
- A9B в 12сс: \(10*12^2+9*12^1+11*12^0\).
Такой записи числа достаточно, чтобы перевести значение числа из любой системы счисления в 10сс — нужно посчитать значение составленной записи:
- \(1010_2=1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=10_{10}\);
- \(525_9=5*9^2+2*9^1+5*9^0=5*81+2*9+5*1=428_{10}\);
- \(A9B_{12}=10*12^2+9*12^1+11*12^0=10*144+9*12+11*1=1559_{10}\).
Мы рассмотрели алгоритм перевода числа из Nсс в 10сс. А если мы хотим перевести не в 10сс? Тогда нам нужно выполнить 2 перевода! Сначала перевести в 10сс, а затем из 10сс в нужную. Для этого также существует алгоритм, который мы рассмотрим далее.
Перевод из 10сс в Ncc
Принцип деления с остатком поможет переводить числа в другую сторону — из 10сс в любую другую систему счисления.
Алгоритм перевода числа из 10 сс в другую позиционную систему счисления
1. Делим исходное число на основание новой системы счисления.
2. Остаток от деления — новая найденная цифра числа.
3. Целую часть от деления снова делим на основание. Записываем остаток как новую цифру искомой записи, а целую часть от деления — как цель следующего деления. Снова делим целую часть на основание.
4. Деление происходит до тех пор, пока целая часть от деления не станет равна 0.
5. Полученные в качестве остатков от деления цифры нового числа читаются в обратном порядке.
Для примера давайте переведем число 2589 в 7сс:
- На первом шаге делим исходное число на 7, записывая остаток от деления как новую цифру и целую часть как оставшееся значение.

- На втором шаге делаем то же самое, но с целой частью предыдущего деления — теперь делим ее на 7.

- И так до тех пор, пока целая часть от деления не будет равна 0.



Интересующее нас значение находится в самом правом столбце и читается снизу вверх:
\(2589_{10}=10356_7\)
Перевод в системы счисления с основанием больше 10 происходит так же. Просто надо не забывать, что цифры больше 9 будут обозначаться соответствующими буквами.
Например, таблица перевода десятичного числа 48406 в 16сс будет выглядеть следующим образом:

И искомое значение будет BD16.
Лайфхак или как быстрее закодировать геном
Представим, что нам нужно написать программу для биологов, которую они будут применять в исследованиях ДНК, и нам надо реализовать хранение ДНК в памяти компьютера.
В ДНК встречается четыре вида азотистых оснований: аденин (A), гуанин (G), тимин (T) и цитозин (C). Всю ДНК можно записать как последовательность этих 4 символов. Но можно же записать тогда эту последовательность букв как число в 4сс, сопоставив цифры символам, например, код A – 0, C – 1, G – 2, T – 3. Тогда кусок ДНК GGT будет записан в 4сс как 223.
Но, чтобы закодировать геном в компьютере, его надо перевести из 4сс в 2сс. Делать это делением может оказаться очень долго, ведь геном может быть очень длинным и делить его просто неэффективно. К счастью, есть выход.
Между 2сс и системами счисления, в основании которых стоит степень двойки (4сс, 8сс, 16сс), есть связь, которую можно использовать для быстрого перевода из 2сс в них и обратно. Для этого используется следующая таблица:
| 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 |
Алгоритм перевода чисел между 2сс и другими системами, основание которых является степенью двойки
1. Вычисляется степень, в которую нужно возвести 2, чтобы получить основание необходимой системы счисления (\(2сс — 2^1, 4cc — 2^2, 8cc — 2^3\) и т.д.).
2. Используется количество столбцов таблицы, равное этой степени. Отсчет ведем с правого столбца (2сс — один столбец справа, 4сс — два столбца справа, 8сс — три столбца справа и т.д.).
3. При переводе из 2сс весь код разбивается на кодовые слова длиной, равной степени (2сс — по 1, 4сс — по 2, 8сс — по 3) — при необходимости в начало записи добавляются нули. Отдельные кодовые слова подставляются в нижнюю строку таблицы. Цифра записи числа в новой системе счисления будет равна сумме цифр верхней строки, под которыми стоит 1 кодового слова.
4. При переводе в 2сс каждая цифра представляется как сумма цифр верхней строки таблицы. Цифрам, которые используются в сумме, соответствуют 1 кодового слова 2сс, а не использующимся — 0.
Для перевода между 2сс и 4сс используется часть таблицы (\(2^2=4\), берем 2 столбца справа):
| 2 | 1 |
| 1 | 1 |
Посмотрим на пример перевода числа \(110001_2\) из 2сс в 4сс:
- Разбиваем число на части длиной, равной 2. Так как длина — 6, то в начало нули не добавляем: 11.00.01.
- Отдельно подставляем каждый блок, отделенный точкой, в нижнюю строку таблицы.
- Для 1 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас единицы есть под 2 и под 1, тогда сумма для 1 блока: 2+1=3.
| 2 | 1 |
| 1 | 1 |
- Для 2 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас нигде нет единиц в нижней строке, поэтому сумма тут равна 0+0=0.
| 2 | 1 |
| 0 | 0 |
- Для 3 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас единица только под 1, поэтому сумма для 3 блока: 0+1=1.
| 2 | 1 |
| 0 | 1 |
- Запишем отдельно суммы для каждого блока. Получим итоговый ответ в 4сс:
\(110001_2 = 11.00.01 = (2 + 1).(0 + 0).(0 + 1) = 3.0.1 = 301_4\)
Разберем еще один пример.
Перевод числа \(103_4\) из 4сс в 2сс:
- Разделяем каждую цифру точкой для удобства.
- Каждую цифру представляем в виде суммы верхней строки:
- Для 1: 0*2+1*1=0+1=1.
- Для 0: 0*2+0*1=0+0=0.
- Для 3: 1*2+1*1=2+1=3.
- Запишем отдельно для каждой цифры суммы.
- Если число есть в верхней строке нашей таблицы — будет 1, иначе — 0. Затем уберем точки и получим результат (0 так и останется 0, ибо его нет в верхней строке, 1 и 2 — станут 1, так как они есть в верхней строке).
\(103_4 = 1.0.3 = (0 + 1).(0 + 0).(2 + 1) = 01.00.11 = 10011_2\)
Для перевода между 2сс и 8сс используется часть таблицы (\(2^3=8\), берем 3 столбца справа):
| 4 | 2 | 1 |
| 1 | 1 | 1 |
Перевод числа \(10101011100_2\) из 2сс в 8сс:
- Разбиваем число на блоки длиной, равной 3. Так как длина — 11, то в начало добавим один 0, чтобы образовать тройку в начале: 010.101.011.100.
- Отдельно подставляем каждый блок, отделенный точкой, в нижнюю строку таблицы.
- Для 1 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас единицы есть под 2, тогда сумма для 1 блока: 0+2+0=2.
| 4 | 2 | 1 |
| 0 | 1 | 0 |
- Для 2 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас есть единицы под 4 и 1, тогда сумма: 4+0+1=5.
| 4 | 2 | 1 |
| 1 | 0 | 1 |
- Для 3 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас единица под 2 и 1, поэтому сумма для 3 блока: 0+2+1=3.
| 4 | 2 | 1 |
| 0 | 1 | 1 |
- Для 4 блока. По правилу, где в нижней строке стоят единицы — суммируем верхние числа. У нас единица есть только под 4, сумма: 4+0+0=4.
| 4 | 2 | 1 |
| 1 | 0 | 0 |
- Запишем отдельно суммы для каждого блока. Получим итоговый ответ в 8сс.
\(10101011100_2 = 010.101.011.100 =\)
\(= (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1) .(4 + 0 + 0)=\)
\(= 2.5.3.4 = 2534_8\)
Перевод \(1753_8\) из 8сс в 2сс:
- Разделяем каждую цифру точкой для удобства.
- Каждую цифру представляем в виде суммы верхней строки:
- Для 1: 0*4+0*2+1*1=0+0+1=1.
- Для 7: 1*4+1*2+1*1=4+2+1=7.
- Для 5: 1*4+0*2+1*1=4+0+1=5.
- Для 3: 0*4+1*2+1*1=0+2+1=3.
- Запишем отдельно для каждой цифры суммы.
- Если число есть в верхней строке нашей таблицы — будет 1, иначе — 0 (в верхней строке есть 4, 2, 1 — они будут 1, остальные — 0). Затем уберем точки и получим результат.
\(1753_8 = 1.7.5.3 = (0 + 0 + 1).(4 + 2 + 1).(4 + 0 + 1).(0 + 2 + 1) =\)
\(= 001.111.101.011=1111101011_2\).
Таблицы триад и тетрад
После таких долгих вычислений задаешься вопросом: «Можно ли быстрее переводить числа из одной системы счисления в другую?». Да, конечно! Со временем был придуман более удобный способ — табличный. С его помощью можно без особых усилий получить нужный результат.
Предыдущий алгоритм работает довольно быстро, но его сложно применять, потому что надо внимательно складывать числа, можно ошибиться или забыть выполнить какое-то действие.

Можно просто запомнить соотношения между двоичными числами и цифрами 8сс и 16сс вместо того, чтобы их считать! Для этого есть таблицы, которые легко можно построить самостоятельно.
Для 8сс таблица двоичных триад (чисел из 3-х знаков), таблица будет выглядеть так:
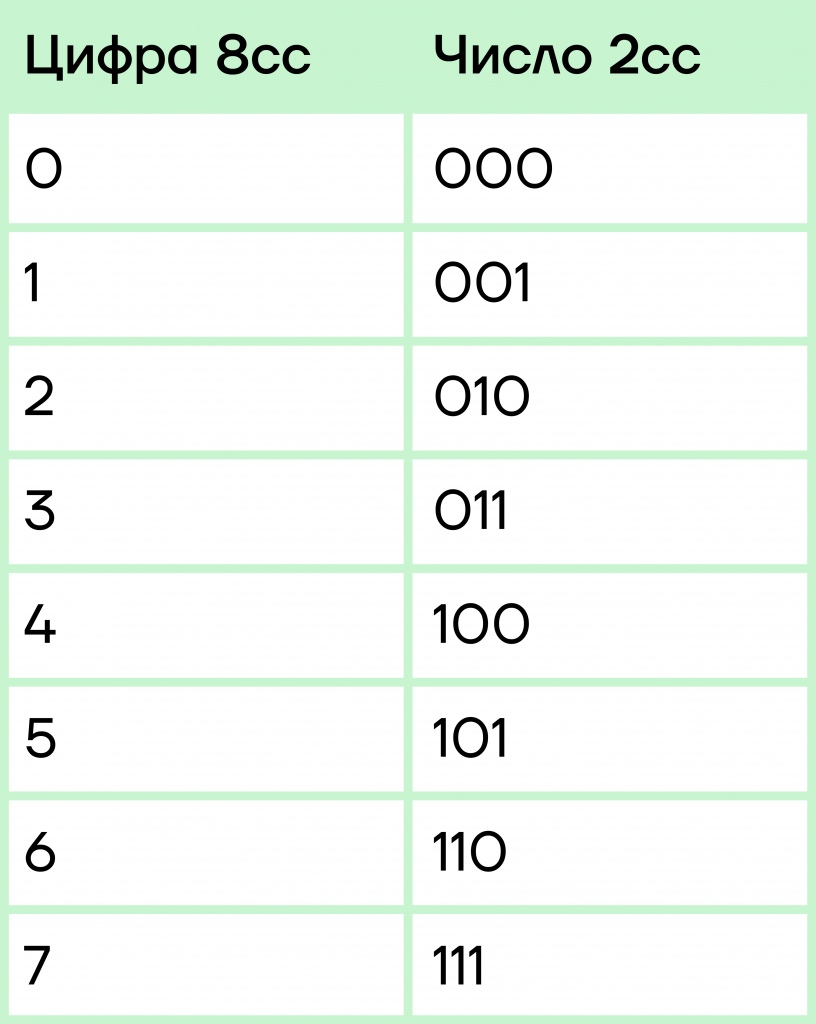
Как же получить эти значения? Просто перевести все числа от 0 до 7 из 10сс в 2сс. А если обратить внимание, то можно увидеть закономерность в их написании — последняя цифра числа чередуется — 0101…, цифры посередине чередуются по 2 — 001100…, а первые чередуются по 4 — 00001111.
Для 16сс уже нужны тетрады — числа из 4 двоичных знаков. Их таблица выглядит так:
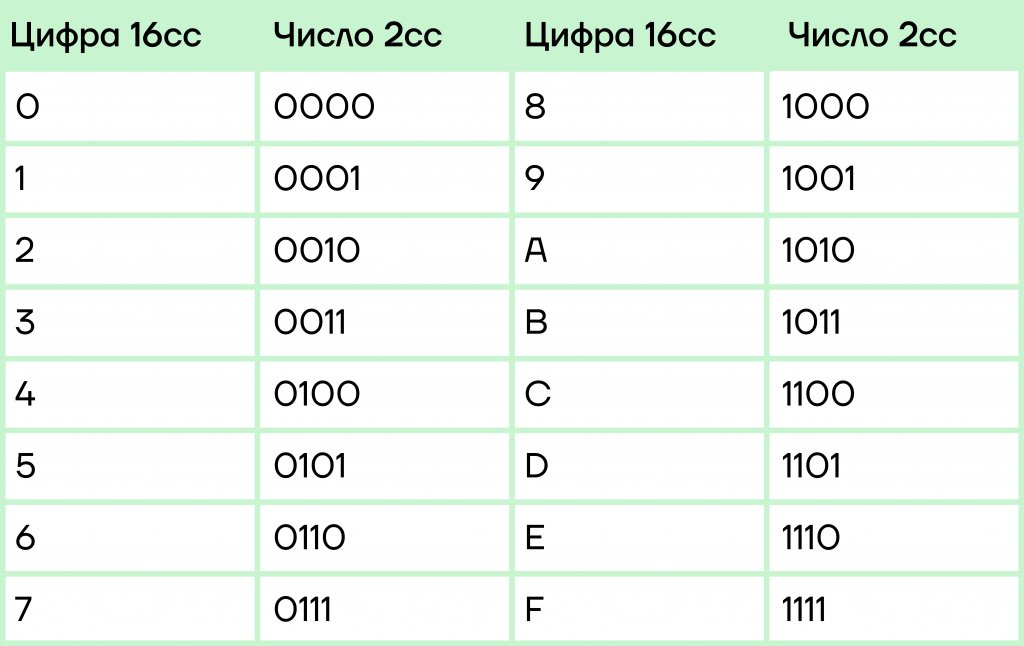
Теперь, чтобы перевести число 15748 в 2 сс, мы просто подряд записываем двоичные числа, соответствующие нашим цифрам: 001 101 111 100. Остается только убрать ведущие нули (то есть незначащие нули слева в записи блока наподобие 0010), и перевод завершен. Результат — 1101111100.
А чтобы перевести число 100001110101101 в 16сс, его нужно разбить на блоки из 4 цифр (деление на блоки начинаем с конца), при необходимости дописав ведущие нули: 0100 0011 1010 1101. Теперь каждой тетраде мы сопоставляем ее цифру в 16 сс и получаем 4 3 A D. Результат перевода – 43AD.
| А если межгалактическая торговля нам все-таки доступна? Используя полученные навыки, можно слетать на космическую ярмарку и все же купить шоколадку. Допустим, что на планете «Двойск» жители используют только 2сс в обычной жизни. Два раза в год они проводят ярмарку, на которой можно приобрести множество вещей со всех планет космоса. На ярмарку прилетела цивилизация с планеты «Восьмерка», использующая 8 сс. Они хотят купить шоколадку. Продавец установил цену — 1000101011 в 2сс. Посмотрим, сколько им нужно заплатить. Поделим число на блоки из 3 цифр, дописав ведущие нули: 001 000 101 011. Теперь с помощью таблицы сопоставим цифру из 8сс: 1 0 5 3. Теперь инопланетяне с «Восьмерки» знают, сколько им нужно заплатить, чтобы купить шоколадку! |

Со временем в различных системах счисления начали появляться различные операции и особенности, которые используются в разработке, науке и программировании. Познакомимся с некоторыми из них!
Особенности разных систем счисления
За счет того, что в 2сс только две разные цифры, в ней появилась нестандартная операция — инверсия. Так называется процедура замены всех цифр двоичного числа на противоположные. Например, инверсия от 100010 — это число 011101.
Также во всех системах счисления легко можно проверять четность числа.
В системах счисления с четным основанием число четно тогда и только тогда, когда четна его последняя цифра.
Это связано с особенностью строения позиционных систем. Вспомним, как выглядит число в системе счисления с основанием n:
\(a_1a_2a_3…a_i…a_k=a_1*n^{k — 1}+a_2*n^{k — 2}+…+a_i*n^{k — i}+…+a_k*n^0\)
Если n четно, то в правой части равенства четны все слагаемые, у которых есть n в виде множителя. Тогда единственное возможно нечетное слагаемое – это последняя цифра, которая необязательно делится на n.
Существует также способ проверки четности у числа, записанного в нечетной системе счисления.
В системах счисления с нечетным основанием число четно тогда и только тогда, когда четна сумма его цифр.
Принцип работы этого правила похож на привычный нам признак деления на 3 и на 9 в 10сс, который также опирается на сумму цифр числа. Посмотрим несколько примеров:
- \(1211_3\): сумма цифр -1+2+1+1=5, тогда число – нечетное (в 10сс – 49);
- \(4615_7\): сумма цифр -4+6+1+5=16, тогда число – четное (в 10сс – 1678).
Есть быстрый способ складывать и вычитать разные степени оснований, который используется для вычисления различных выражений.
Правила при вычислении выражений в различных системах счисления
1. Допустим, в системе счисления с основанием n надо посчитать \(n^k+n^l\), где \(k > l: n^k+n^l=n^l*(1+n^k-l )\). При этом первая группа из нулей имеет длину \(k-l-1\), а вторая — \(l\).
2. Число же \(n^k-n^l\) равно \(n^l*(1-n^k-l)\). Соответственно, в конце его записи мы также видим \(l\) нулей, но перед ними будет стоять \(k-l\) раз цифра \(n-1\).
3. Если же требуется вычесть какое-то число \(f\), не являющееся степенью основания, то имеет смысл найти такую степень \(m\), что \(n^m>f\), вычесть ее по формуле выше, а затем прибавить число \(n^m-f\).
4. Когда в выражении имеется несколько разностей подряд, то можно использовать следующую формулу: \(-n^k= -n^{k+1}+(n-1)*n^k\).
Примеры:
- Найдем значение выражения \(5^5+5^2\) в 5 сс. По первому правилу получается, что первая группа из нулей имеет длину \(5-2-1=2\). А вторая — 2. Между ними — 1. Тогда получается: \(5^5-5^2=100100_5\).
- Найдем значение выражения \(5^5-5^2\) в 5 сс. По второму правилу в конце будет два нуля, а перед ними будет стоять \(5-2=4\) раза цифра \(5-1=4\). Например, \(5^5-5^2=44400_5\).
- Найдем значение выражения \(5^5-13\) в 5 сс. По третьему правилу представим число в другом виде. Например, запись \(5^5-13\) можно превратить в \(5^2-25+12=5^5-5^2+12=44400_5+22_5\).
- Найдем значение выражения \(5^5-5^4-5^3\) в 5 сс. Используем сначала четвертое правило. Получим: \(5^5-5^5+4*5^4-5^3= 4*5^4-5^4+4*5^3=3*5^4+4*5^3\). По первому правилу получаем, что первая группа нулей имеет длину \(4-3-1=0\), вторая — 3. А первая цифра — 3, так как нулей нет в первой группе, то сразу после 3 — 4. Тогда ответ — \(34000_5\).
Когда мы изучили теоретический материал, можем поговорить об особенностях перехода между системами счисления на Python.
Перевод между системами счисления на Python
Перевод больших чисел между системами счисления вручную неудобен и может занимать много времени. Почти всегда оптимальнее было бы написать программу.
Перевод из 10сс в другие будем выполнять по описанному выше «Алгоритму перевода числа из 10 сс в другую позиционную систему счисления». Пока исходное число больше 0, делим его на основание системы счисления. Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.
- Основным циклом программы будет while, который работает, пока исходное число больше 0.
- Новую цифру числа берем как остаток от деления исходного числа на основание новой системы счисления с помощью оператора %. Новые цифры будем записывать в новую строку, в которой и будет храниться искомая запись. Чтобы не переворачивать число в конце, можем сразу заносить каждую новую цифру не в конец, а в начало строки.
- Уменьшаем само число, деля его нацело на основание с помощью оператора //.
Рассмотрим в качестве примера перевод числа 258936 в 5сс.
number = 258936
n = 5 new_number = «»
while number > 0:
d = number % n
new_number = str(d) + new_number
number //= n
print(new_number)
Вывод программы: 31241221
Перевод в 10сс из других систем счисления будем производить по описанной выше формуле:
\(a_1a_2a_3…a_i…a_k=a_1*n^{k — 1}+a_2*n^{k — 2}+…+a_i*n^{k — i}+…+a_k*n^0\).
- Главный цикл программы — for. Он будет перебирать цифры исходного числа, а точнее их индексы, с помощью диапазона range по длине исходного числа.
- На каждом шагу цикла цифру \(a_i\) числа мы будем умножать на основание системы счисления этого числа n в степени, равной разности длины числа k и порядкового номера текущей цифры \(i — a_i*n^{k — i}\) . Не забываем, что индексация строки начинается с 0, а не с 1, поэтому порядковый номер цифры — на 1 больше ее индекса.
Например, переведем число 31241221 из 5сс обратно в 10сс.
number = «31241221»
n = 5
new_number = 0
k = len(number)
for i in range(k):
new_number += int(number[i]) * n ** (k — i — 1)
print(new_number)
Вывод программы: 258936
Лайфхаки по переводу между системами счисления программой:
- Для перевода числа из 10сс в 2сс, 8сс и 16сс в Python есть встроенные команды: bin, oct и hex соответственно:
- bin(123) — “0b1111011”
- oct(123) — “0o173”
- hex(123) — “0x7b”
Важно заметить, что первые два символа в записи числа окажутся лишними в нашем случае — они будут обозначать идентификатор системы счисления, в которую мы перевели число.
Чтобы сразу от него избавиться, при переводе можно использовать срез, который будет учитывать все число без этого идентификатора:
- bin(123)[2:] — “1111011”
- oct(123)[2:] — “173”
- hex(123)[2:] — “7b”
- Перевести число из любой системы счисления, основание которой не превышает 36, в 10сс можно с помощью команды int. Ей необходимо передать два параметра: исходное число в виде строки и основание его системы счисления:
- int(«31241221», 5) — 258936
- int(«7b», 16) — 123
Зачем знать все это, если мы не генетики и не торгуем с инопланетянами? Системы счисления — одно из базовых понятий информатики и оттого используется в большом количестве заданий на ЕГЭ. С применением различных систем счисления придется столкнуться при решении задачи 14, при построении большинства алгоритмов задачи 5, в заданиях на расчет объема информации в номере 7.
Попробуем решить задачу 14 ЕГЭ с применением Python.
Значение арифметического выражения: \(2771^{111}-530^{44}+330^{20}-2344\) записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение:
1. Записываем данное число в переменную. Чтобы возвести число в степень, используем оператор **:
s = 2771**111 — 530**44 + 330**20 — 2344
2. Объявляем переменную, в которой будем хранить количество подходящих цифр:
count = 0
3. Запускаем цикл while. Он нам нужен для того, чтобы перебирать все цифры числа s. Делаем условием цикла s > 0, потому что если переменная s стала равна 0, значит, все цифры закончились:
while s > 0:
4. Делаем проверку, является ли последняя цифра числа s в троичной системе счисления двойкой. Взятие остатка от деления на 3 как раз дает последнюю цифру числа в троичной системе счисления:
if s % 3 == 2:
5. Увеличиваем счетчик на 1, если условие выше выполнилось:
count += 1
6. «Отсекаем» последнюю цифру (которую мы только что рассмотрели) от числа с помощью целочисленного деления. Делим на 3, так как нам нужно работать в троичной системе счисления:
s = s // 3
7. Выводим результат:
print(count)
Полный код программы:
s = 2771**111 — 530**44 + 330**20 — 2344
count = 0
while s > 0:
if s % 3 == 2:
count += 1
s = s // 3
print(count)
Вывод программы: 248
Подведем итог.
Для чего нам разные системы счисления?
- Системы счисления — одно из базовых понятий информатики и оттого используются в большом количестве заданий на ЕГЭ.
- Работа с разными системами счисления необходима в информатике, математике и программировании, где двоичная система счисления часто используется для представления данных в компьютерах.
В этой статье мы изучили и проанализировали алгоритмы перевода чисел из одной системы счисления в другую, разобрали несколько примеров на эту тему, а также узнали, как купить шоколадку у инопланетянина. Теперь подобные задачи не будут вызывать трудностей. Приглашаем вас продолжить изучение программирования и освоить новые решения для своих задач в статье «Функции и рекурсия».
Фактчек
- В позиционных системах счисления, в отличие от непозиционных, значение цифры зависит от ее положения в числе.
- Основание позиционной системы счисления определяет количество используемых в ней цифр для записи чисел, а также от четности основания зависит правило определения четности/нечетности числа.
- Для перевода из 10сс в любую другую: берем остаток от деления на основание новой системы счисления в качестве цифр нового числа и записываем их в обратном порядке.
- Для перевода из любой системы счисления в 10сс: умножаем каждую цифру числа на основание его системы счисления, возведенную в степень разности длины числа и порядкового номера данной цифры.
- В Python для перевода числа из 10сс в 2сс, 8сс и 16сс есть встроенные команды: bin, oct и hex соответственно. А перевести число из любой системы счисления, основание которой не превышает 36, в 10сс можно с помощью команды int.
Проверь себя
Задание 1.
Какая цифра не может использоваться в 8сс?
- 0
- 3
- 7
- 8
Задание 2.
Для записи цифр 10—15 в 16сс используются …
- буквы A—F
- буквы А—Д
- буквы U—Z
- любые символы по договоренности
Задание 3.
Если число FBA000 из 16сс перевести в 10сс, то оно будет выглядеть …
- 16490496
- 69409461
- 61400900
- это некорректная запись числа в 16сс
Задание 4.
Что сделает запись int(“777”, 8) на языке Python?
- переведет число 777 из 10сс в 8сс
- переведет число 8 из 10сс в 777сс
- переведет число 777 из 8сс в 10сс
Задание 5.
Какое число четное?
- \(1211_3\)
- \(101_2\)
- \(B23_{15}\)
Ответы: 1. — 4; 2. — 1; 3. — 1; 4. — 3; 5. — 3.


 к списку статей
к списку статей



