Алгебра логики

На этой странице вы узнаете

• Что такое алгебра логики и при чем здесь котики?
• Зачем в алгебре логики правило — «Два по цене одного»?
• Для чего нужны законы логики?

Алгебра логики – наука, которая позволяет нам логически мыслить и делать выводы. Она находит применение в различных областях науки и техники начиная от разработки компьютерных алгоритмов до создания сложных систем управления и автоматизации производства. Однако, это не только практически полезная наука, но и увлекательная, которая может заинтересовать широкий круг людей. 

Давайте погрузимся в мир алгебры логики и узнаем, как она помогает нам решать различные задачи! Например, как часто поведение котов вам кажется странным? А если вы встретите кота в галстуке, что вы скажете? А если говорящего кота? Разберемся же в логике с помощью этих милых и пушистых созданий!

Понятие алгебры логики

Обратите внимание на этого важного персонажа:

Допустим, про него сказано две вещи:

A — «Этот кот в галстуке».
B — «Этот кот белого цвета».

С первым высказыванием и поспорить нельзя, а вот второе — очевидная ложь. А если кто-то захочет вас запутать: «Этот кот в галстуке или он белого цвета». Что это в итоге — правда или ложь? Чтобы это определить, в математике есть отдельный раздел.

Для начала давайте разберемся в том, что же такое алгебра логики.

Алгебра логики — это раздел математики, который занимается логическими операциями над высказываниями.

Высказывание — любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Рассмотрим примеры высказываний:

• Бабочка – это насекомое.
• На поле растут бананы.
• Котики летают на Марс.

Любое высказывание может быть либо истинным, либо ложным. Цель алгебры логики — определять истинность логических выражений на основании отдельных высказываний. Алгебра логики действительно может, например, складывать и умножать высказывания друг с другом. Чтобы пользоваться принятыми правилами было удобно, истину принято обозначать как 1, а ложь — как 0. 

Давайте рассмотрим более подробный пример. Допустим, что у нас есть два утверждения:
A – «Все котики любят молоко», при этом оно истинно, тогда \(A=1\).
B – «Этот котик любит печенье», а это ложно, тогда \(B=0\).

Как говорилось ранее, мы можем складывать и умножать высказывания друг с другом. На самом деле эти операции могут заменяться знакомыми словами для удобства, например И, ИЛИ, но об этом подробнее мы поговорим далее. Для начала составим несколько выражений в качестве примера:

1. A*B=A И B
   Получим: «Все котики любят молоко» И  «Этот котик любит печенье».

2. A+B=A ИЛИ B
   Получим: «Все котики любят молоко» ИЛИ  «Этот котик любит печенье».

Что такое алгебра логики и при чем здесь котики? Давайте вернемся к нашим котикам, ведь мы так и не выяснили, обманули нас или нет… A – «Этот кот в галстуке». B – «Этот кот белого цвета». В нашем примере высказывание А было истинно, а высказывание В — ложно. Если вспомнить, что истина обозначается — 1, а ложь — 0, то сразу становится понятно, что на языке алгебры логики это было бы записано как А = 1,  В = 0. Не забудьте, ведь это нам пригодится далее при встрече с другим котиком!

Когда мы разобрали базовые понятия, рассмотрели примеры некоторых выражений, высказываний и базовых операторов, хочется подробнее рассказать о том, с чем же на самом деле мы уже столкнулись!

Логические выражения и операторы 

Как вычислить истинность логического выражения?

Термин «высказывание» мы уже знаем. Но что такое логическое выражение? 

Логическое выражение — это уравнение из высказываний, как математическое уравнение из чисел. 

Например, «кот вооружен и его глаза зеленого цвета», — в одном выражении мы использовали два высказывания – «кот вооружен», «его глаза зеленого цвета». 

Истинность выражения определяется истинностью логических высказываний, а также логическими операторами, которые стоят между ними, как мы увидели ранее.

Например, скажем про того же самого кота: «Этот кот вооружен и его глаза голубые». Это будет наглая ложь, так как был употреблен союз И, то есть подразумевается, что оба высказывания истинны — что неправда. Но если сказать: «Этот кот вооружен или его глаза голубые», союз ИЛИ защитил бы от клейма лжеца. В данном случае делается акцент на истинности только одного высказывания из двух. Так как кот действительно вооружен, то можно смело утверждать, что все выражение истинно.

Так и работают логические операторы — в зависимости от них все выражение и принимает значение истины или лжи.

Основные логические операторы алгебры логики:

• Конъюнкция: логическое умножение или логическое И. В записи обозначается как ∧. А ∧ В дает истину только в том случае, если оба высказывания А и В истинны.
  Называется логическим умножением, потому что имеет схожий принцип работы: если хоть один из множителей будет равен 0, все выражение будет равно 0.
  
  В примере про кота выше выражение «Этот кот вооружен ∧ его глаза голубые» будет ложным. Он вооружен, но глаза у него не голубые. Одно из высказываний не выполнилось, так что конъюнкция равна: 1 ∧ 0 = 1 И 0=0.

• Дизъюнкция: логическое сложение или логическое ИЛИ. В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.
  Называется логическим сложением за схожесть: если складывать только 0 и 1, чем мы и занимаемся, то достаточно одному слагаемому быть 1, чтобы все выражение не было равно 0.

Зачем в алгебре логики правило — «Два по цене одного»? Важно сразу понять — если применить логическое сложение к двум единицам (1 ∨ 1), мы получим не 2, а все еще 1. Все-таки единица здесь означает не число, а истину, и, сложив две, мы не получим одну сверхистину, так как принято использовать только 0 и 1.

Тогда выражение «Этот кот вооружен ∨ его глаза голубые» будет уже истинным: глаза его не голубые, но он все-таки вооружен. Дизъюнкция вернет нам 1 ∨ 0 = 1 ИЛИ 0=1.

• Инверсия: логическое отрицание или логическое НЕ. Превращает истину в ложь, и наоборот.
  
  Ложное высказывание «Его глаза голубые» можно легко превратить в истину, если сказать «Его глаза НЕ голубые». В записи обозначается чертой над выражением или знаком ¬, например, ¬А. Например: ¬1 =0 ,   ¬0 =1 .
  Пример: ¬p — «его глаза НЕ голубые», где p — высказывание «его глаза голубые». 

• Эквиваленция, если проще — равенство. Если оба высказывания равны (оба 0 или оба 1), то получим истину, иначе — ложь. Обозначается как ≡.
  
  Истинным будет выражение «У кота нет оружия так же, как его глаза голубые». И то, и другое — ложь, но мы их сравнили, сказав, что они одинаковы по истинности, что уже правда. Пример: 0 ≡ 0 =1 .
  
  Попробуем перевести выражение на математический язык. Пусть у нас есть высказывание «Угол называется прямым тогда и только тогда, когда он равен 90 градусам». Можно перевести это высказывание на математический язык алгебры логики следующим образом:  p  ≡ q, где p — высказывание «угол прямой», q — высказывание «угол равен 90 градусам». 

• Импликация, иначе говоря, следование. Обозначается стрелочкой, например А ⇒ В. Если из истины следует ложь, то это автоматически ложь, все остальное — истина.
  
  Например, вас никто не просил кормить кота. Если вы этого не сделаете, ничего плохого и не случится. А если сделаете — тоже хорошо, кот будет рад. А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.
  
  Попробуем перевести выражение на математический язык. Пусть у нас есть высказывание «Если сегодня идет дождь, то я возьму зонтик». Можно перевести это высказывание на математический язык алгебры логики следующим образом:  p ⇒ q, где p — высказывание «сегодня идет дождь», q — высказывание «я возьму зонтик». 

Довольно часто в информатике применяется такая операция, как поразрядная конъюнкция (побитовое И) — это бинарная операция, действие которой эквивалентно применению логического И к каждой паре битов в двоичной системе счисления (2сс), стоящих на одинаковых позициях в двоичных представлениях операндов. Рассмотрим пример, чтобы было легче понять, что же это такое!

Пусть даны 2 числа (сразу перевели в 2сс): \(a=23_{10}=10111_2\) и  \(b=30_{10}=11110_2\). Нам необходимо найти a&b — поразрядную конъюнкцию. Составим таблицу:

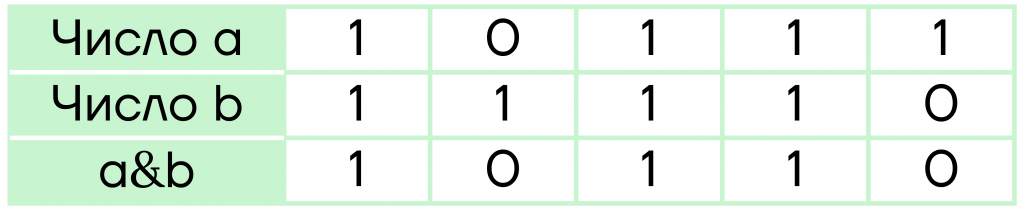
Если длина чисел не совпадает, то к числу с меньшим количеством цифр необходимо дописать нули в начало, пока длина двух чисел не станет равна. В каждую ячейку запишем цифры чисел по горизонтали. Применим к каждому столбцу операцию конъюнкции. Для первого:  \(1∧1=1\). Для второго: \(0∧1=0\). Для остальных аналогично. Получим: \(10110_2\). Это и будет ответом!

Приоритет операторов:

1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация;
5. эквиваленция.

Как в математике при выполнении каких-либо действий существует приоритет операций, так и в алгебре логике также есть свой приоритет операторов. Сделано это для того, чтобы избежать неоднозначности и все могли одинаково трактовать то или иное выражение. Многие знают, что умножение «важнее» сложения, а приоритет можно менять с помощью скобок — что в них, то выполняется в первую очередь. Не забывайте об этих правилах!

В процессе изучения алгебры логики были придуманы специальные таблицы истинности, которые помогают производить операции на сложных и длинных выражениях, а также установить связи между различными высказываниями. Давайте познакомимся с ними более подробно!

Таблицы истинности

В логических уравнениях высказывания используются в виде переменных, а главная проблема, которую рассматривает алгебра логики — когда точно неизвестна истинность каждого высказывания. Назовем эту ситуацию «кот в мешке». Сказать про кота можно что угодно, но будет ли это правдой —  мы не узнаем, пока не заглянем в мешок. В таких ситуациях нам может помочь таблица истинности.

Таблица истинности — это таблица, которая показывает истинность всего логического уравнения в зависимости от истинности отдельных переменных.

В этой таблице содержатся все возможные наборы переменных. Количество наборов N зависит от количества различных переменных \(N=2^n\).
Чтобы удобно записать наборы, нумеруем их по порядку начиная с 0, переводим их номер в двоичную систему счисления (2сс) и записываем набор цифр.

Давайте запишем таблицы истинности для известных нам логических операторов:

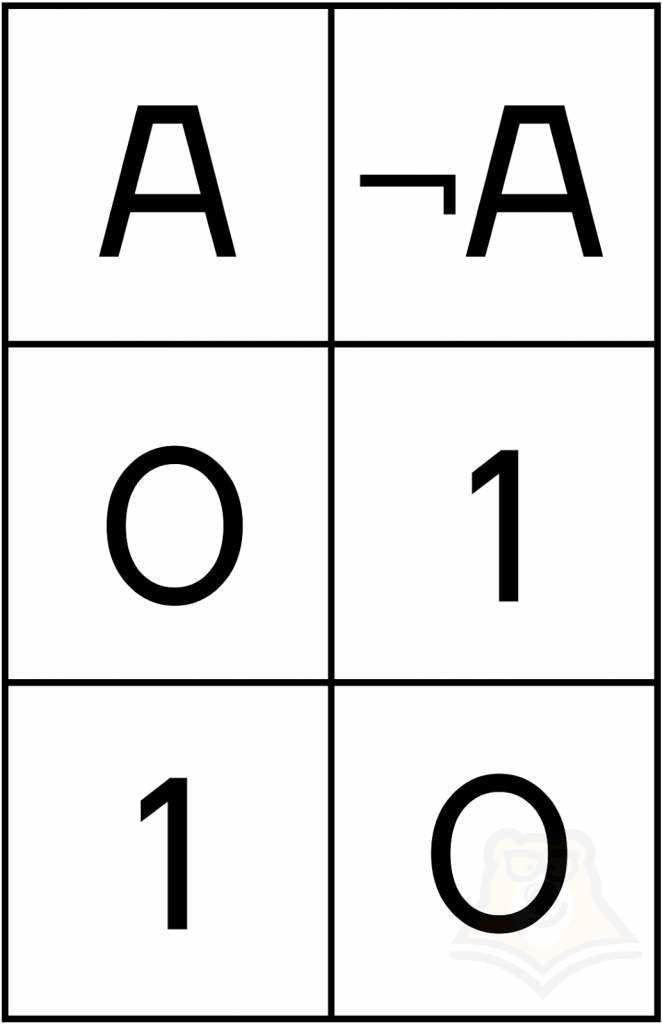
• инверсия берет только 1 переменную и сразу меняет ее значение:

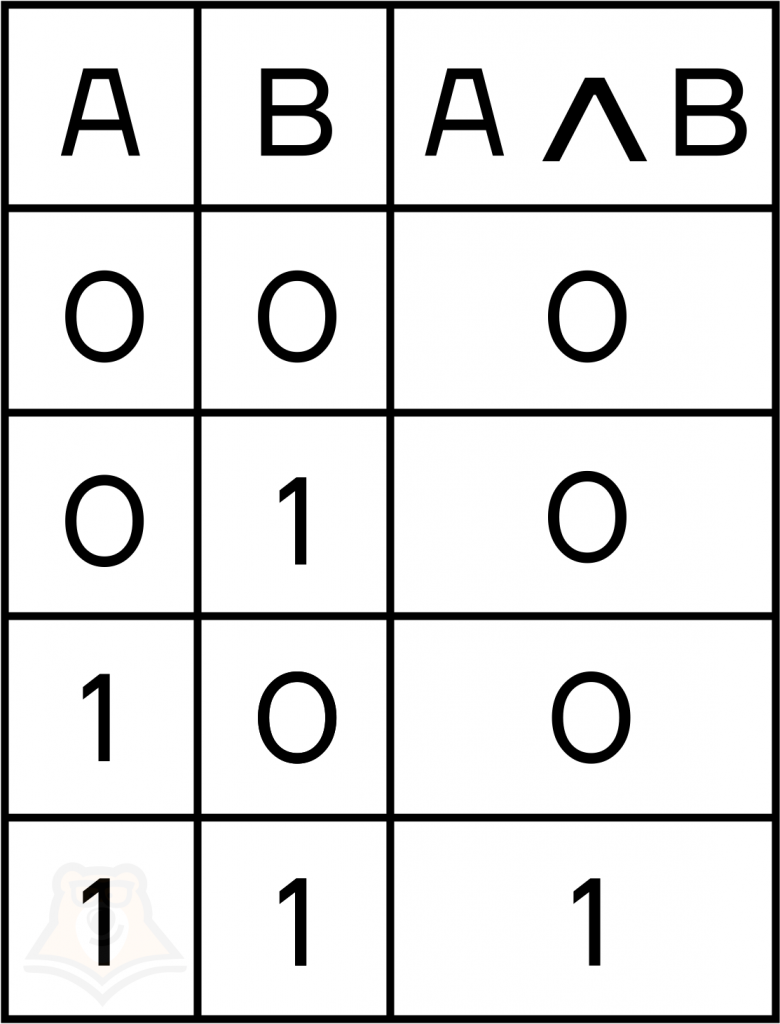
• конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:

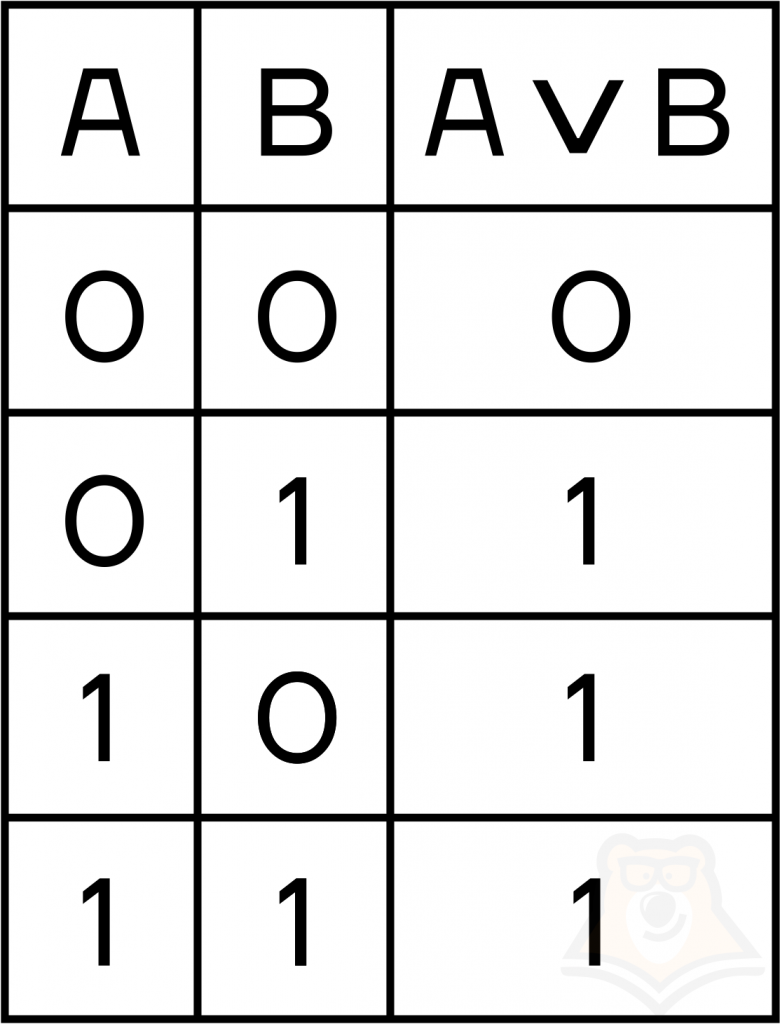
• дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:

• эквиваленция вернет 1, если переменные равны, и 0 в противном случае:

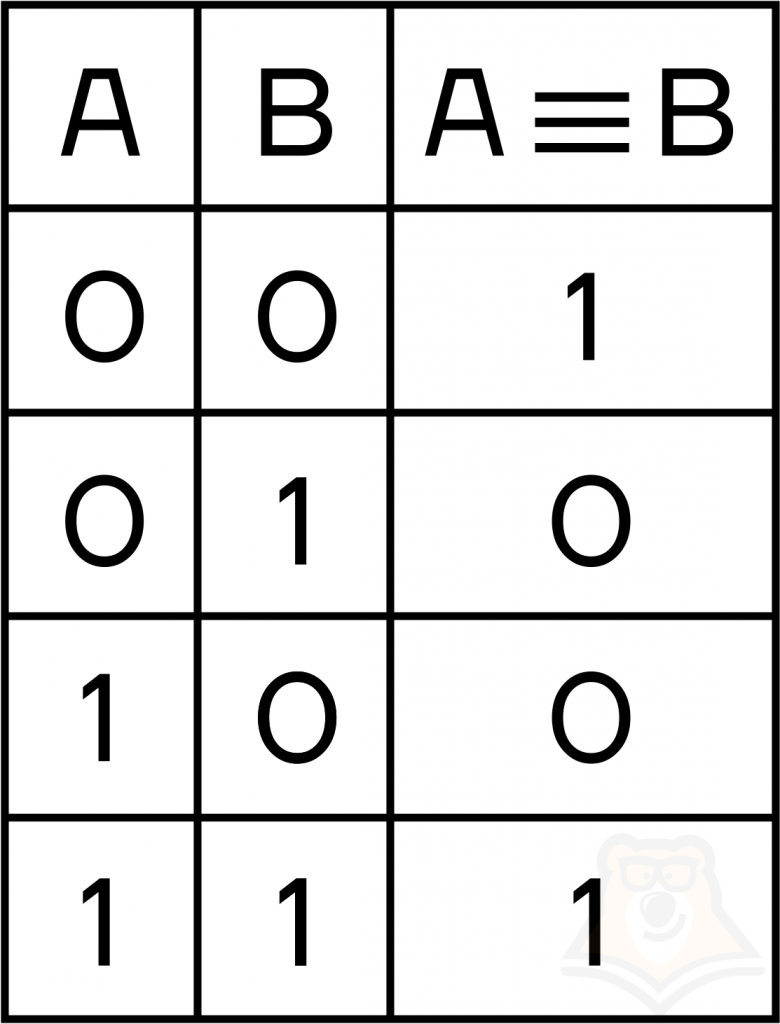
• импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:

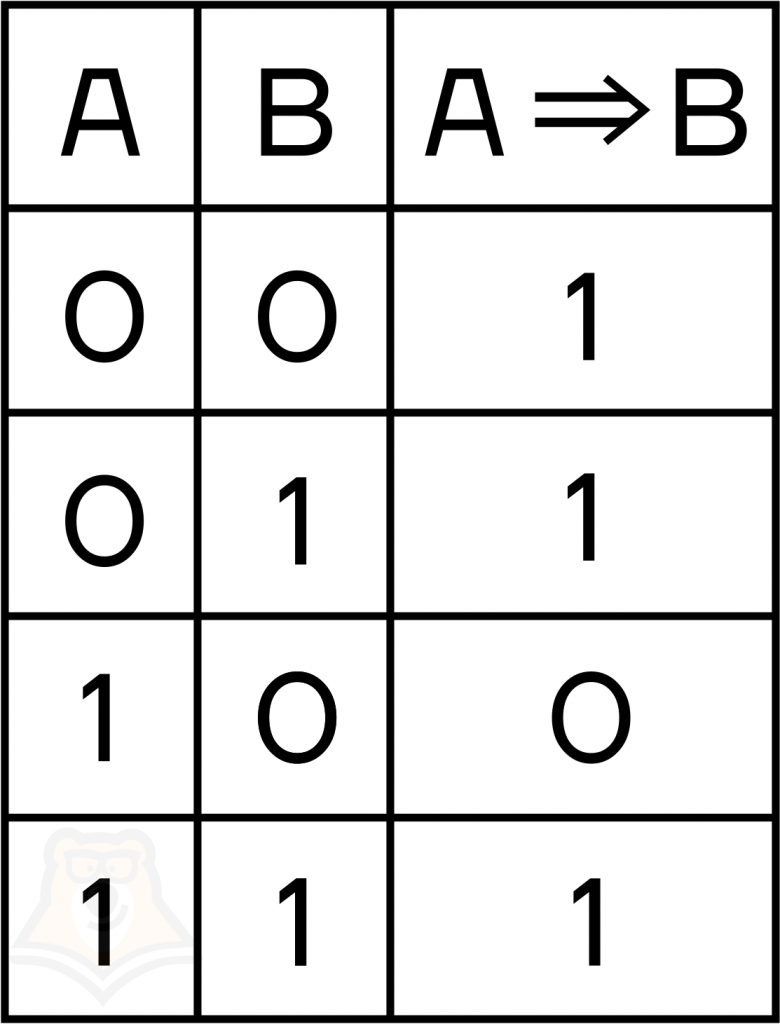
Импликацию можно выразить через дизъюнкцию: \(А ⇒ В = ¬А ∨ В\)

Потренируемся применять полученные навыки на примере задачи 15 номера ЕГЭ.

Задание. Для какого наименьшего значения A выражение:\((x*y>A) ∧ (x>y) ∧ (x<7)\)
тождественно ложно (т.е. принимает значение 0) при любых целых положительных значениях переменных х и y?

Решение.
1. Выражение принимает значение 0, когда хотя бы одна из скобок ложна, так как между ними стоит логическое умножение. При этом A есть только в первой скобке. Нам необходимо рассмотреть предельный случай, когда 2 и 3 скобки – истинны, а первая должна быть ложна. Это даст нам гарантию того, что если 2 и 3 дают истину, то 1 скобка даст ложь — все выражение будет ложно (если хотя бы одно из 2 или 3 даст ложь, то все выражение также будет ложью, нас это не сильно волнует, так как там нет переменной А).

2. Тогда получаем: \(x>y\) и \(x<7\). Так как числа целые, то максимальные значения, которые подходят нам — \(X=6, Y=5\). Если брать меньше, то данные числа не покроют все условия.

3. Первая скобка должна быть ложна, как мы сказали выше. Тогда (\(x* y ≤ A\)). Подставляя значения: \(6* 5 ≤  A\). Тогда минимальное значение \(A = 30\). Заметим, что если брать числа меньше в пункте 2, например \(X=5, Y=3\). То, конечно, А будет меньше, но оно тогда не покроет значения 6 и 5, как мы взяли, а они в данном случае принимают максимальные значения.

Ответ: 30

Зная таблицы истинности отдельных операторов, давайте попробуем составить таблицу истинности для полного выражения.

Например, для выражения: \(А ∧ (В ∨ С) ≡ В ⇒ ¬А\).
Важно правильно расставить порядок операций. Как и всегда, в первую очередь выполняется действие в скобках, а дальше – в порядке приоритета.
Здесь порядок операций будет следующим:

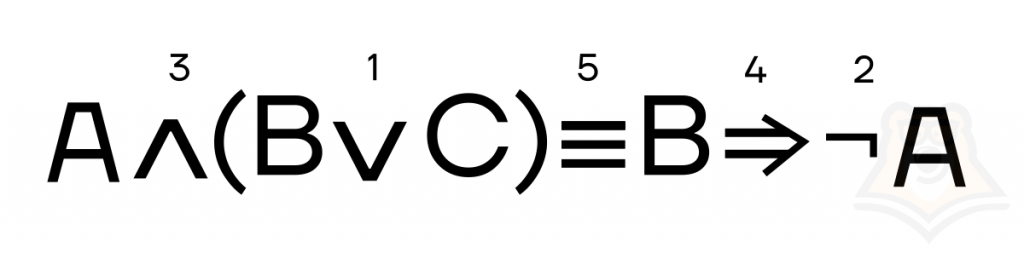
Создадим таблицу, в которой сразу пропишем все наборы 0 и 1 для переменных А, B и C и добавим столбцы для каждого шага вычисления. 

Чтобы было удобно записать наборы, пронумеруем их по порядку начиная с 0. Переведем их номер в 2сс и запишем набор цифр. У нас 3 различные переменные, поэтому должно быть 8 наборов.

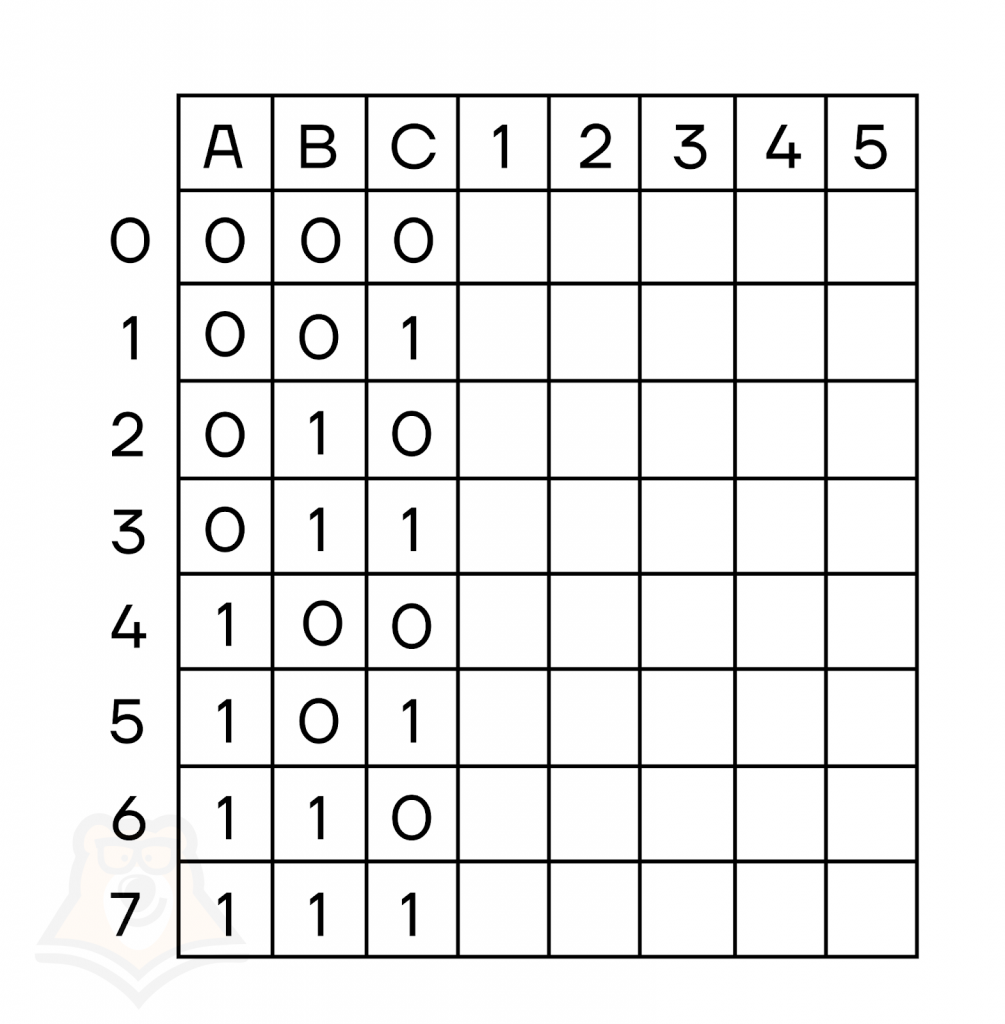
1. Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.

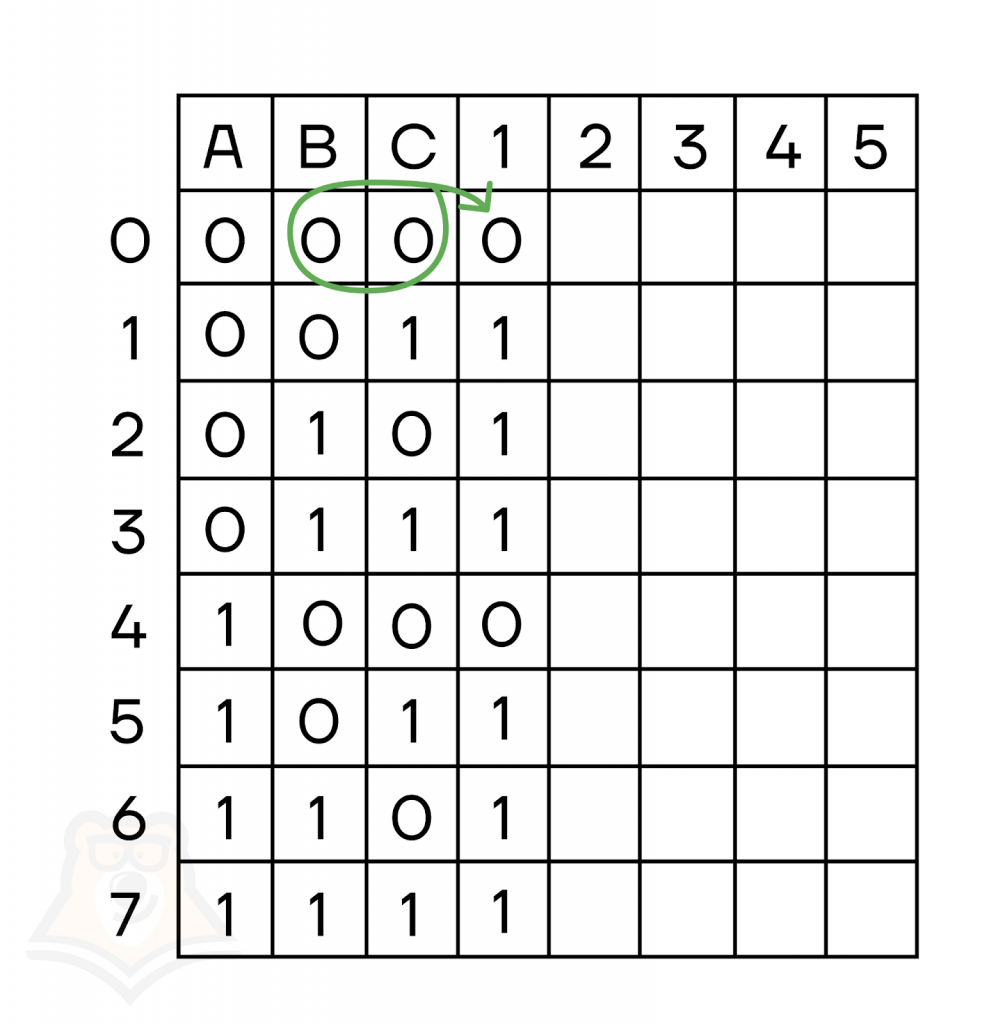
2. Второе действие — инверсия переменной А.

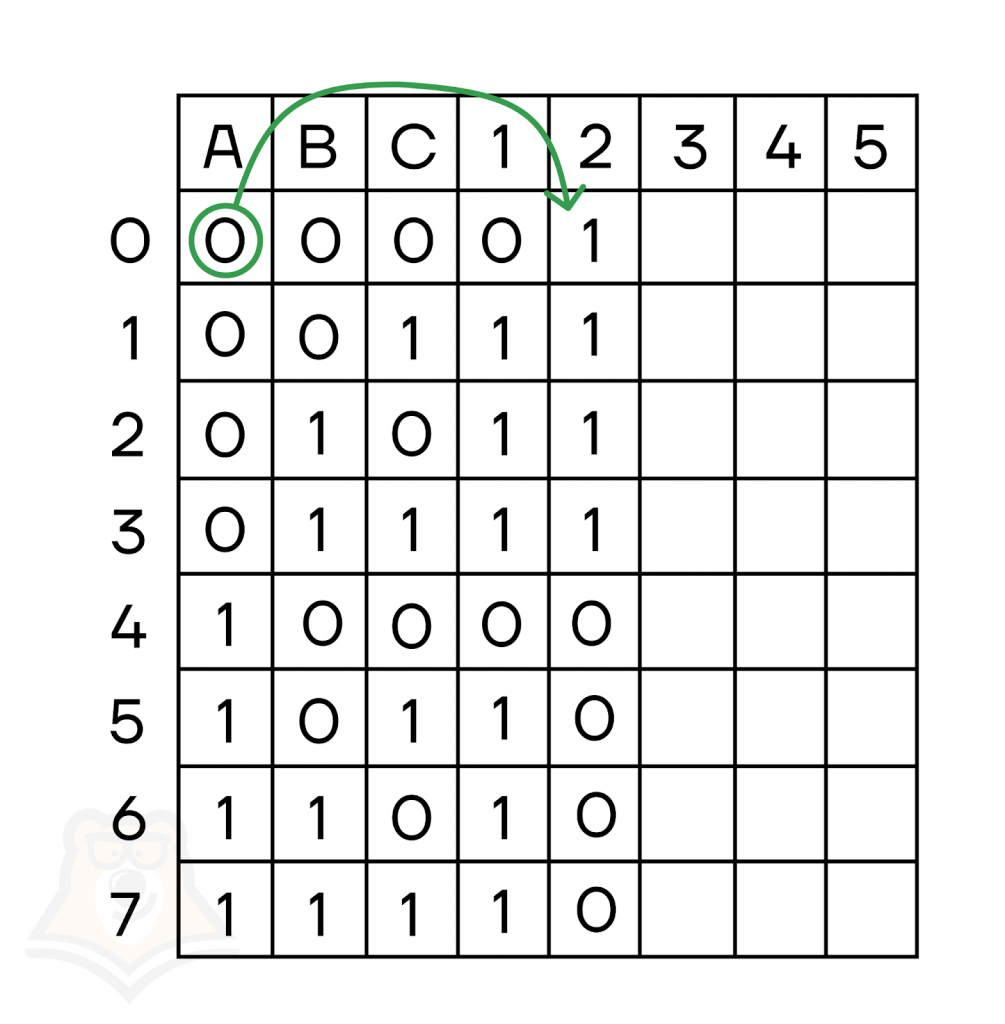
3. Третье действие — умножение значения А на результат первого действия:

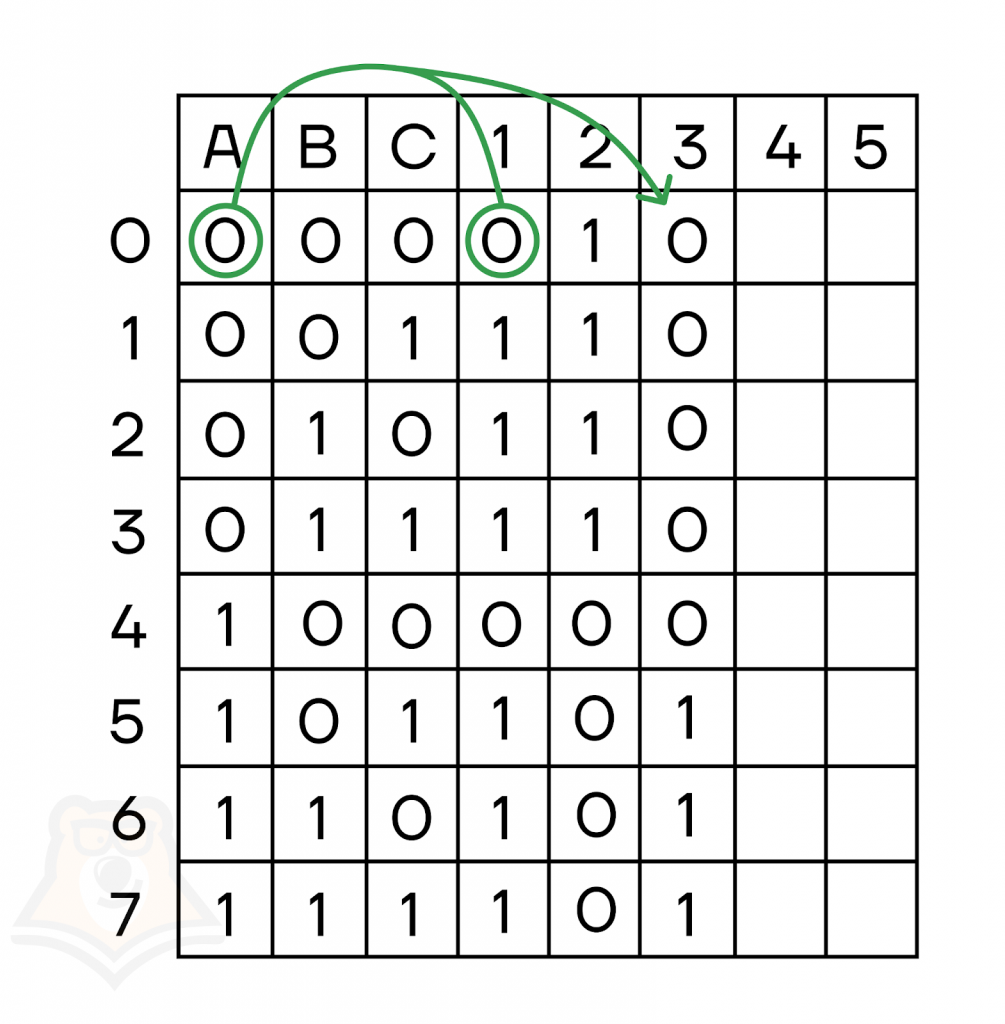
4. Четвертое — импликация значения В и результата второго действия:

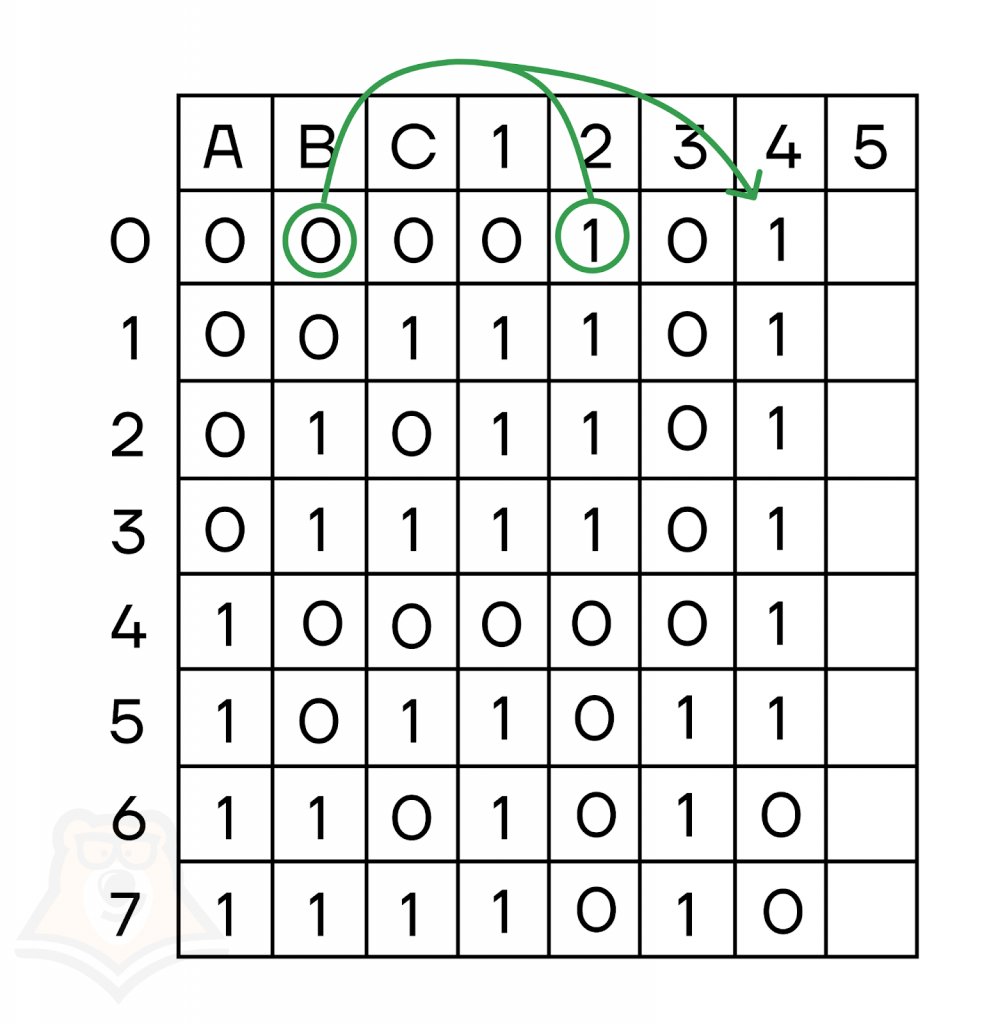
5. И последнее действие — эквиваленция результатов 3 и 4 действий:

Последний столбец — и есть результат таблицы истинности. По нему можно сказать, что при \(А = 1, В = 0\) и \(С = 1\) все исходное выражение равно 1, а во всех остальных случаях — 0.

Познакомимся теперь с законами логики, которые помогут нам научиться преобразовывать логические уравнения, делать их более простыми и понятными!

Законы логики

Для чего нужны законы логики? Законы логики позволяют упрощать логические выражения, делая их не такими большими и более решаемыми.

Их не так уж и мало: от самых простых и очевидных до достаточно хитрых; от тех, которые встречаются очень часто до довольно редких.

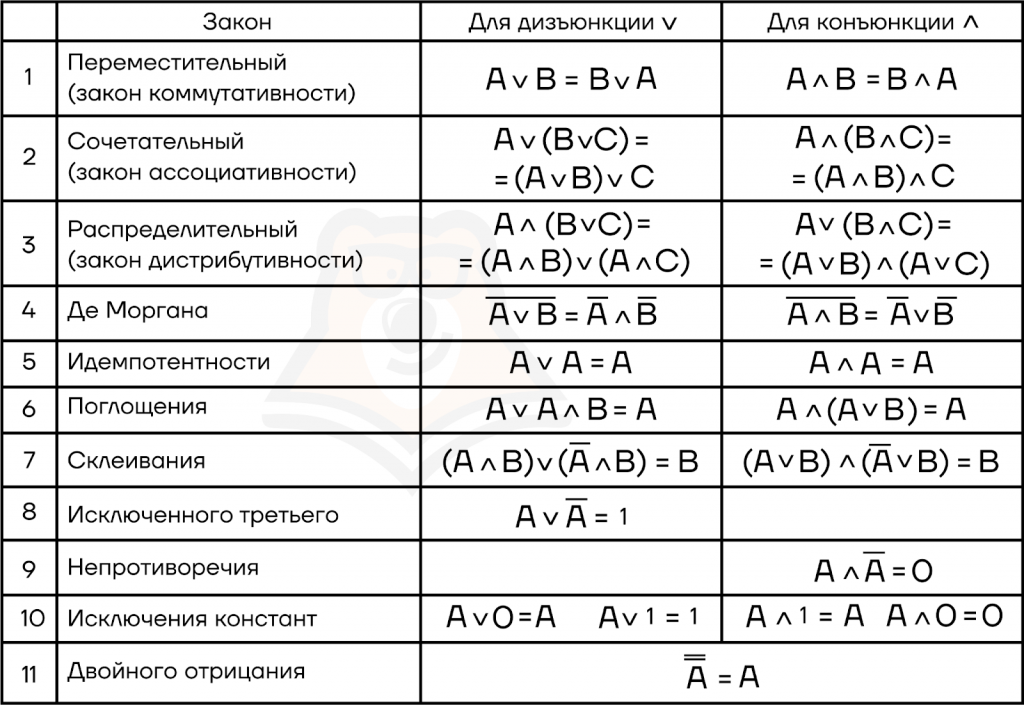
Необязательно знать все наизусть — часть из них действительно проста и похожа на правила математики начальной школы. Например, переместительный закон: \(2+5=5+2\) (от перестановки мест слагаемых их сумма не меняется). Распределительный: \(2*(4+3)=2*4+2*3\). 

Про остальные стоит помнить: если увидите очень большое логическое выражение, высока вероятность того, что эти законы помогут его сократить.

Достаточно часто приходится сталкиваться с заданиями, где нужно подобрать число, удовлетворяющее требованиям уравнения. Для упрощения записи приходится прибегать к рассмотренным законам. Рассмотрим примеры простых задач, где это может понадобиться:

• Необходимо найти наибольшее натуральное X, удовлетворяющее выражению:    (X > 20) И НЕ(X > 22). 
  
  1. Для начала упростим выражение: (X > 20) И (22 ≥ X), то есть (X больше 20) И (X меньше 22 или равен 22).
  2. Тогда наибольшее натуральное такое X лежит в (20, 22]. Тогда X = 22.

• Необходимо найти количество натуральных чисел X, которые удовлетворяют выражению: НЕ(НЕ(X < 13 ) ИЛИ (X < 10)). 

1. Для начала упростим выражение: НЕ((X ≥ 13) ИЛИ (X < 10)), далее: (X < 13) И (X ≥ 10).
2. Тогда (X меньше 13) И (X больше 10 или равен 10), то есть числа лежат в [10, 13). 
3. Нам нужно найти такие натуральные X, удовлетворяющие условию. То есть это – 10, 11, 12. Всего три таких числа. Ответ — 3.

Также есть более сложные выражения, которые упрощаются в нескольких шагах. Попробуем упростить исходное выражение ¬(¬А ∧ ¬В) ∨ В ∧ С:

1. Первым можно увидеть закон де Моргана, где у нас идет отрицание целой скобки:
   ¬(¬А ∧ ¬В) ∨ В ∧ С = ¬(¬А) ∨ ¬(¬В) ∨ В ∧ С

2. Здесь же появляются переменные А и В, к которым можно применить закон двойного отрицания:
   ¬(¬А) ∨ ¬(¬В) ∨ В ∧ С = А ∨ В ∨ В ∧ С

3. Можно заметить закон поглощения — В складывается с умножением В на С:
   А ∨ В ∨ В ∧ С = А ∨ В

Итого уравнение с 3 переменными и множеством отрицаний мы смогли превратить в максимально простую запись, где осталось всего 2 переменные:

¬(¬А ∧ ¬В) ∨ В ∧ С = А ∨ В

Рассмотрим еще один пример возможного задания из №15 ЕГЭ. 

Задание. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула:
(ДЕЛ(x, 2) ⇒  ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 100)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?

Решение.
1. Сначала упростим формулу. Вспомним, что А ⇒ В = ¬А ∨ В. Тогда применим это к нашему выражению, получим:
(¬ДЕЛ(x, 2) ∨ ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 100).

2. Выражение принимает значение 1, когда хотя бы одна из скобок истинна. При этом A есть только во второй скобке. Допустим, что мы возьмем такие значения X, при которых в первой скобке — ложь, тогда во второй должна быть истина, чтобы все выражение было истинно. Если же в первой истина, то уже и не так важно, что во второй. То есть необходимо рассмотреть случай, когда первая скобка дает ложь, а затем подобрать такие A, при которых вторая будет истинна. 

3. Тогда ¬(¬ДЕЛ(x, 2) ∨ ¬ДЕЛ(x, 5)). Преобразуем по закону де Моргана: (ДЕЛ(x, 2) ∧  ДЕЛ(x, 5))=1. То есть – (X делится без остатка на 2) И (X делится без остатка на 5). Именно такие числа будут давать в первой скобке ложь. Теперь рассмотрим вторую скобку (x + A ≥ 100).

4. Вторая скобка (x + A ≥ 100) должна быть истинна при таких X — (X делится без остатка на 2) И (X делится без остатка на 5), как мы рассмотрели выше. Рассмотрим несколько натуральных значений X:
1) X = 10, тогда (10 + A ≥ 100), A ≥ 90;
2) X = 20, тогда (20 + A ≥ 100), A ≥ 80;
3) X = 30, тогда (30 + A ≥ 100), A ≥ 70…

Увидим, что A = 90 — наименьшее значение, которое будет покрывать условие при X = 10. При увеличении X, если взять A меньше, как ответ, то A будет покрывать не все значения. Например, при A = 80 будут покрыты условия во 2, 3… При этом в 1 нет, ибо 10 + 80 = 90, а это меньше 100.

Ответ: 90

В этой статье мы познакомились с алгеброй логики, освоили множество новых и полезных операций, которые обязательно нам еще пригодятся! Приглашаем познакомиться с не менее интересной статьей «Алгебра логики в программировании», посвященной применению алгебры логики и решению практических задач.

Термины

Двоичная система счисления  —  это система счисления, в которой числа представляются с помощью двух цифр  — 0 и 1. Каждый разряд имеет два возможных значения: 0 или 1.

Операнд  — это элемент математической операции, на который действует оператор. Например, в операции 2+5=7, операнды  — числа 2 и 5.

Фактчек

• Алгебра логики — это математика, которая пользуется не числами, а высказываниями, являющимися истинными или ложными. Истина обозначается как 1, а ложь — как 0.
• Основными логическими операторами являются инверсия (логическое отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (логическое следование) и эквиваленция (логическое равенство).
• Для расчета истинности логического уравнения используется таблица истинности.
• Иногда требуется перевести текст на математический язык, чтобы работать с ним согласно правилам алгебры логики.
• Законы логики помогают сокращать логические уравнения.

Проверь себя

Задание 1.
Выберите правильный порядок приоритета логических операторов:

1. Импликация, эквиваленция, конъюнкция, дизъюнкция, инверсия.
2. Инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция.
3. Инверсия, конъюнкция, дизъюнкция, эквиваленция, импликация.
4. Инверсия, дизъюнкция, конъюнкция, эквиваленция, импликация.

Задание 2.
Сопоставьте название логического оператора с упрощенным:

Инверсия	А. Умножение
Эквиваленция	Б. Отрицание
Импликация	В. Следование
Дизъюнкция	Г. Равенство
Конъюнкция	Д. Сложение

Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения: А ∨ В ⇒ ¬С?

1. 11101010
2. 11101111
3. 11111110
4. 11000100

Задание 4.
Сократите логическое выражение: ¬(А ∨ В) ∧ (¬А ∨ С)

1. ¬(А ∧ В)
2. ¬А ∨ ¬В ∨ С
3. ¬А ∧ ¬В ∧ С
4. ¬А ∧ ¬В

Задание 5.
Найдите значение выражения A&B, если \(A =10111_2, B =100_2\)

1. 000
2. 100
3. 00010
4. 1000

Ответы: 1. – 2; 2. – 1Б, 2Г, 3В, 4Д, 5А; 3. – 1; 4. – 4; 5. – 2